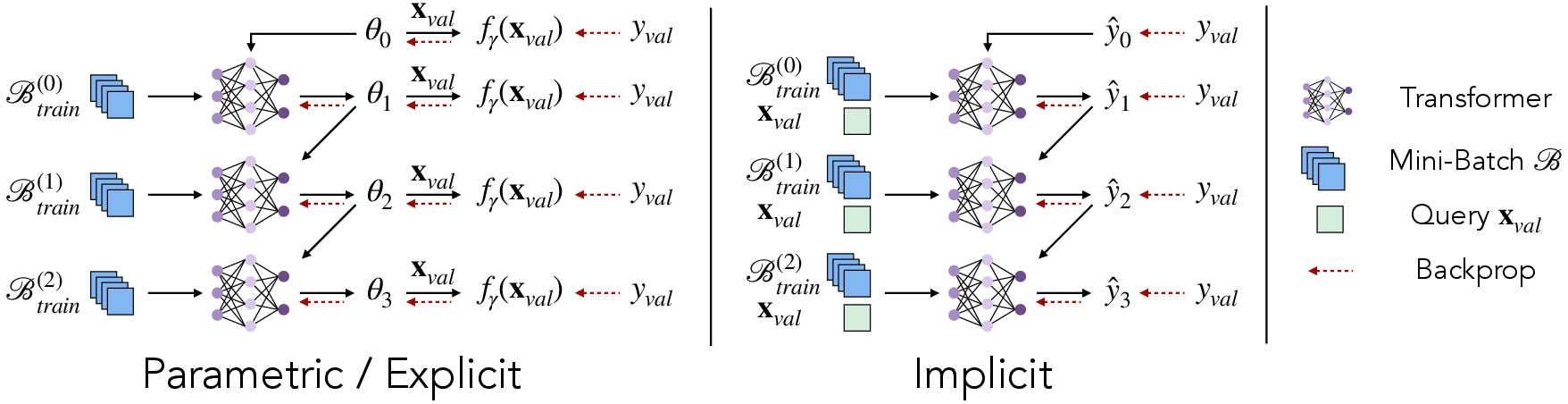
Iterative Amortized Inference: Unifying In-Context Learning and Learned Optimizers (2510.11471v1)
Abstract: Modern learning systems increasingly rely on amortized learning - the idea of reusing computation or inductive biases shared across tasks to enable rapid generalization to novel problems. This principle spans a range of approaches, including meta-learning, in-context learning, prompt tuning, learned optimizers and more. While motivated by similar goals, these approaches differ in how they encode and leverage task-specific information, often provided as in-context examples. In this work, we propose a unified framework which describes how such methods differ primarily in the aspects of learning they amortize - such as initializations, learned updates, or predictive mappings - and how they incorporate task data at inference. We introduce a taxonomy that categorizes amortized models into parametric, implicit, and explicit regimes, based on whether task adaptation is externalized, internalized, or jointly modeled. Building on this view, we identify a key limitation in current approaches: most methods struggle to scale to large datasets because their capacity to process task data at inference (e.g., context length) is often limited. To address this, we propose iterative amortized inference, a class of models that refine solutions step-by-step over mini-batches, drawing inspiration from stochastic optimization. Our formulation bridges optimization-based meta-learning with forward-pass amortization in models like LLMs, offering a scalable and extensible foundation for general-purpose task adaptation.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper is about “learning to learn.” Instead of training a brand-new model from scratch for every new problem, the authors describe ways for a model to reuse what it learned before so it can adapt quickly to new tasks. They show that popular ideas like in-context learning (how LLMs use examples in the prompt), meta-learning (learning a good starting point), and learned optimizers (learning how to train) are actually different versions of the same big idea. Then, they introduce a new method called iterative amortized inference, which helps models handle lots of task data by improving their answers step by step, using small chunks of data.
What questions are they asking?
- How are different “learning to learn” methods connected under one simple framework?
- What are the main types of these methods, and how do they trade off speed, flexibility, and scalability?
- Why do many current methods struggle when they must look at a lot of examples at once (like long prompts)?
- Can we design a method that adapts to a new task by refining its answer gradually, using mini-batches (small batches) of examples, so it scales better?
How do they approach it?
First, some simple analogies to explain key terms:
- Amortized learning: Imagine practicing math problems until you get so good at recognizing patterns that you can solve new problems quickly by reusing what you’ve learned. You “amortize” (spread out) the cost of learning across many tasks.
- In-context learning (ICL): Like a student who looks at a few examples in the question and figures out the rule without changing their long-term memory.
- Learned optimizer: Like a coach who has learned a great training routine and gives you smart, customized exercise updates instead of using a basic one-size-fits-all plan.
- Mini-batches: Reading and understanding a long textbook chapter-by-chapter instead of all at once, improving your notes as you go.
- Gradients: Hints that tell you which direction to adjust your model to make fewer mistakes.
The authors build a unified view with two parts: 1) A shared mechanism that captures general knowledge across tasks. 2) A task adaptation function that uses new task data to adjust what the model does.
Using this, they define a simple taxonomy of three types:
- Parametric: The prediction model is fixed, and another learned model produces the right parameters for the task. Think: a fixed recipe (prediction model), but you learn how to pick the best ingredients for each dish (task parameters). Examples: learned optimizers and hypernetworks.
- Implicit: One big model reads the task examples and the question together and directly predicts the answer—no explicit task parameters are shown. Think: a skilled chef who adapts on the fly just by tasting while cooking. Example: in-context learning in transformers.
- Explicit: You learn both a compact summary of the task (like a “task code”) and a prediction model that uses that code. Think: first write a short shopping list (task summary), then follow a recipe that understands that list.
Key limitation they identify: Many methods can’t easily use large amounts of task data at inference time (for example, long-context prompts are expensive), or they compress the data too much and lose detail.
Their solution: Iterative Amortized Inference (IAI)
- Instead of trying to understand all task data at once, the model improves its solution in small steps.
- At each step, it looks at a mini-batch (a small set) of task examples and updates its current guess.
- This is inspired by how stochastic gradient descent trains models efficiently on huge datasets—by using small batches repeatedly.
They apply this step-by-step refinement to all three types (parametric, explicit, implicit) and allow the refinement to use data directly, gradients, or both.
What did they find, and why is it important?
Here are the main takeaways from experiments across many tasks (like linear regression, digit/image classification using MNIST, FashionMNIST, ImageNet features, causal graph tasks, and generative tasks like drawing letters or sampling from mixtures of Gaussians):
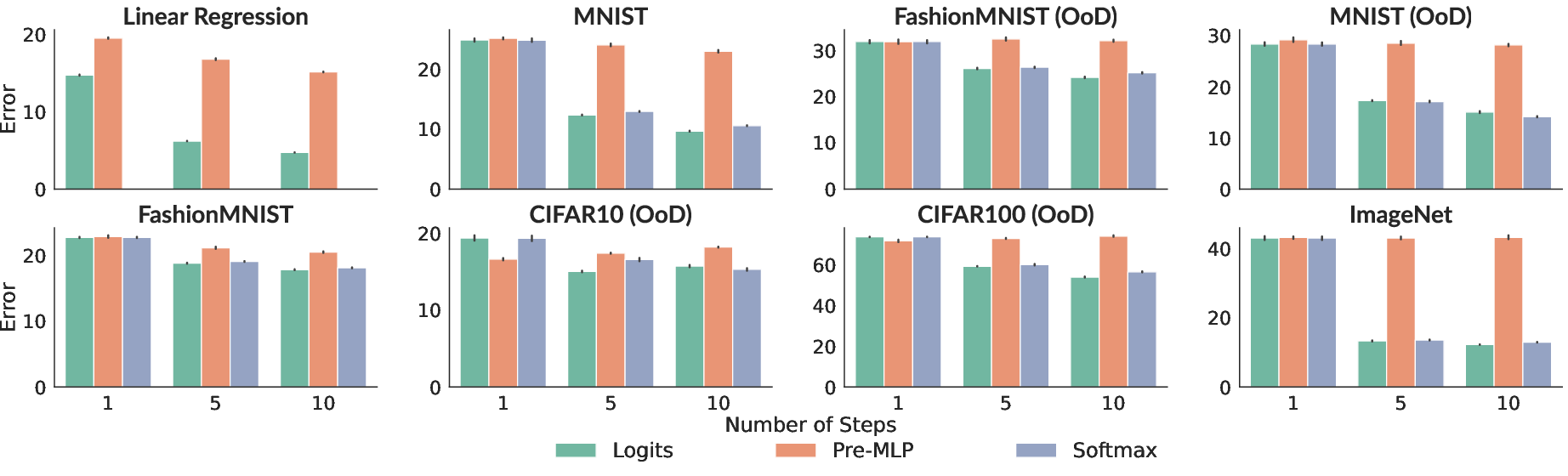
- Taking multiple small steps helps a lot:
- Doing 5–10 refinement steps usually beats doing just 1 step.
- This holds for both in-distribution (similar to training tasks) and out-of-distribution (quite different from training tasks) situations.
- Works across different styles:
- Parametric, explicit, and implicit methods all benefit from the iterative approach.
- Implicit models (like in-context learning) especially gain from refining predictions step by step, improving accuracy and sample quality in generative tasks.
- Using both data and gradients can be better than using only one:
- If you only use gradients (like many learned optimizers), you might miss useful patterns in the raw data.
- Combining direct data and gradient hints often performs best, especially in smaller or mid-sized tasks.
- In tougher, higher-dimensional tasks, gradients can be essential to guide learning effectively.
- Efficiency and scalability:
- Iterative refinement with mini-batches is more efficient than trying to cram all data into one giant context.
- For the same total amount of data processed, the iterative method can be around K times more efficient than a one-shot approach that reads everything at once.
- Design details matter:
- For implicit models, carrying the “logits” (the raw scores before softmax) from one step to the next works better than carrying earlier or later representations. This makes the step-by-step corrections more direct and effective.
- Explicit methods (learning the task summary and the prediction model together) can be harder to train well than parametric methods, even though in theory they are more flexible. The reason is that both parts must co-adapt during training, which is tricky.
Why this matters: These findings show that a simple idea—refine your answers step by step using mini-batches—unlocks better performance and scaling across very different “learning to learn” styles. It also helps models handle bigger task datasets without exploding memory or compute.
What could this change in the future?
- One framework, many tools: The paper unifies several important ideas—meta-learning, learned optimizers, and in-context learning—so researchers and engineers can mix and match them more easily.
- Better adaptation with big data: The iterative approach gives a practical way for models to adapt to new tasks with large amounts of context, without needing giant one-shot prompts.
- More general-purpose AI assistants: Systems could become more “plug-and-play,” adapting to new problems by reading small batches of examples and improving their guesses in a few quick steps.
- Next steps: The authors suggest exploring smarter ways to train these iterative refiners (for example, using reinforcement learning or evolutionary methods) and developing richer forms of memory that persist across steps and tasks.
In short, this work shows how to connect multiple “learning to learn” methods and introduces an efficient, scalable way for models to adapt to new tasks by refining their predictions step by step—much like how people paper: a bit at a time, getting better with each pass.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, consolidated list of what remains missing, uncertain, or unexplored in the paper, framed to be concrete and actionable for future research.
- Lack of theoretical guarantees: no convergence, stability, or monotonic-improvement proofs for the proposed greedy, single-step training of iterative amortized inference (IAI) across parametric, explicit, and implicit regimes.
- Conditions for success are unspecified: the paper does not characterize when (in terms of task families, data regimes, model class, and mini-batch schedules) IAI will provably outperform one-shot amortization or standard optimization.
- No analysis of error propagation across steps: the impact of greedy single-step training on multi-step performance, compounding approximation error, or bias–variance trade-offs is not studied.
- The computational complexity claims (e.g., O(KB2) per K steps and batch size B) are stated but not rigorously derived, profiled, or validated across architectures; memory–speed trade-offs are not quantified.
- Gradient vs data conditioning: there is no principled criterion or adaptive mechanism for when to rely on gradients, observations, or both; the paper reports task-dependent outcomes without generalizable guidance.
- Implicit models cannot leverage gradient signals straightforwardly; open design questions remain for constructing gradient-like signals (e.g., through auxiliary latent heads, implicit differentiation, or query-conditioned Jacobians).
- Explicit models underperform on complex tasks (e.g., ImageNet), but training pathologies (non-stationarity between fγ and gθ, bilevel coupling, optimization instabilities) are not analyzed or mitigated (e.g., via alternating updates, trust-region schemes, auxiliary losses).
- Decomposition non-uniqueness: the paper notes that fγ and gθ partitions are arbitrary yet provides no formal criteria or diagnostics to enforce a query-independent gθ and query-dependent fγ separation in practice.
- Persistent state design in implicit models is ad hoc (logits outperform softmax), but there is no principled framework for state representations (for classification, regression, and generative tasks), nor analysis of calibration, uncertainty, or robustness implications.
- Markovian vs non-Markovian updates: limited ablations on short histories (small k) leave open how longer memory, replay, or external memory modules alter generalization and stability.
- Mini-batch scheduling is under-specified: no paper of ordering effects, curriculum, sampling strategies (stratified vs uniform), or how support-set coverage affects adaptation quality.
- Task distribution assumptions are informal: the paper lacks a precise characterization of “shared inductive biases” and does not paper robustness to task mis-specification, heterogeneous task families, or adversarially constructed tasks.
- Limited scale and scope: experiments cap sequence lengths at 100 and primarily use moderate-size transformers; there is no assessment of scalability to truly large context windows, long sequences, or distributed settings.
- Heavy reliance on pretrained encoders (e.g., DINO-v2 for ImageNet) is not disentangled from amortization benefits; end-to-end training on raw pixels, encoder choice, and representation–amortization interactions remain unexplored.
- Baseline coverage is narrow: comparisons omit strong non-amortized baselines (e.g., fine-tuning with modern optimizers, retrieval-augmented methods), modern ICL in LLMs, and meta-learning methods beyond MAML/hypernetworks/learned optimizers.
- Uncertainty quantification is missing: parametric and explicit regimes do not evaluate posterior or predictive uncertainty, calibration, or risk-sensitive metrics, despite interpretability claims.
- Generative modeling scope is limited: only flow matching with low-dimensional GMMs and alphabet datasets is tested; scaling to high-dimensional continuous/discrete generative tasks (diffusion, autoregressive models) and complex densities is open.
- Multi-query adaptation is not addressed: how amortized states (latents or logits) should be shared, cached, or updated across multiple queries for the same task is unclear.
- Continual/online adaptation and concept drift: the framework’s behavior under non-iid streams, delayed labels, and evolving task distributions is not evaluated.
- Robustness is untested: no analysis of noisy or corrupted contexts, gradient noise, adversarial contexts, or sensitivity to subsampling strategies and outliers.
- Interpretability claims (e.g., parametric regimes yielding human-readable parameters) are not substantiated with concrete case studies or metrics.
- Bilevel optimization alternatives are hinted (RL, evolutionary strategies) but not instantiated; the benefits over greedy single-step training remain hypothetical.
- No exploration of second-order or implicit differentiation methods that could improve explicit regime training or enable gradient use in the implicit regime.
- The taxonomy boundaries are fuzzy: criteria to classify methods as parametric/explicit/implicit and to transition between regimes (e.g., via architectural changes) are not formalized.
- State capacity and dimensionality are not studied: how latent/state size affects information retention, overfitting to context, and generalization is unknown.
- Sample efficiency and data requirements are not quantified; no learning-curve analyses across steps, batch sizes, or task variety.
- Calibration, fairness, and privacy concerns in cross-task amortization are not considered (e.g., task leakage, bias transfer, privacy-preserving adaptation).
- Code availability, reproducibility details (hyperparameters, compute budgets, seeds), and sensitivity analyses are absent, hindering independent verification.
- Order sensitivity and symmetry: whether the iterative updates are invariant to permutation of context samples is not tested; architectural invariances (set vs sequence models) need evaluation.
- Continuous-time refinement (neural ODE views) and connections to control/optimization theory are not explored, despite the iterative update framing.
- Formal links to posterior predictive learning (PFNs/ICL) and learned optimizers are qualitative; precise equivalences or reduction proofs are missing.
Practical Applications
Immediate Applications
Below are deployable applications that can leverage the paper’s iterative amortized inference (IAI) framework now, using standard ML tooling (e.g., PyTorch/JAX, Transformers), retrieval infrastructure, and common MLOps patterns.
- Adaptive fine-tuning pipelines for enterprise ML (Software/MLOps)
- What: Wrap existing models with an iterative adaptation loop that processes task data in mini-batches (instead of one large context or one-shot pooling) to produce per-task parameters, prompts, or predictions. Useful for quickly adapting models to new customers, teams, or datasets without full retraining.
- How: Add a learned “adapter” gϕ that updates task-specific state (weights, soft prompts, or latent task embeddings) over K batches, and a prediction model fγ that consumes the current state for queries. Choose parametric (fixed f, learned g), implicit (learned f, identity g), or explicit (learned f and g) depending on constraints.
- Tools/workflows:
- Iterative Adapter SDK: a library that exposes hϕ and rγ modules for mini-batch updates; plug-ins for Hugging Face Transformers and PyTorch Lightning.
- Task Latent Store: persist per-task latents from gϕ(Dtrain) for reuse, A/B testing, and rollback.
- Dependencies/assumptions: Access to related tasks for meta-training; compute for transformer-based hϕ/rγ; stable data interfaces for streaming mini-batches; distribution shift similar to meta-training tasks.
- Streaming in-context learning beyond context windows (Software/NLP)
- What: Turn ICL from single-pass prompting into a streaming mini-batch process that incrementally refines query predictions as more evidence arrives (e.g., long documents, large retrieval sets).
- How: Use the paper’s implicit iterative scheme rγ([x, ŷ(i)], batch(i)) → ŷ(i+1) to update predictions with batches of examples retrieved from a vector DB.
- Tools/workflows:
- StreamICL: a service that manages chunked retrieval, causal masking, and per-query state updates for LLM inference.
- Dependencies/assumptions: Prompt formatting and masking to maintain causal updates; retrieval quality; careful latency budgeting as K grows.
- Learned optimizers for faster, more stable training (Software/AutoML)
- What: Replace hand-designed optimizers (e.g., Adam) with task-specialized learned optimizers that update weights using gradients and/or data batches, improving convergence on families of tasks.
- How: Use parametric amortization where hϕ ingests (θ(i), ∇θ(i), batch(i)) and outputs θ(i+1); train greedily for single-step improvement as in the paper.
- Tools/workflows:
- Learned Optimizer Hub: pre-trained hϕ models specialized for CNNs, Transformers, or diffusion models; drop-in optimizer API.
- Dependencies/assumptions: Meta-training on representative architectures/tasks; gradient access; guardrails to prevent optimizer-induced instabilities.
- Rapid site/device adaptation in medical imaging and sensors (Healthcare)
- What: Adapt models to a new scanner/site/device using streaming batches from the new domain (calibration shifts, protocols) without full re-training.
- How: Use explicit amortization (learn fγ, learn gϕ) where gϕ infers a low-dimensional site latent; refine it iteratively with batches to reduce validation loss.
- Tools/workflows:
- Site Embedding Cache: persist per-site latents for imaging pipelines (MR/CT/ultrasound), sensor networks, or wearables.
- Dependencies/assumptions: Regulatory constraints (no automated clinical deployment without validation); privacy-preserving meta-training; sufficient similarity between pre-training and target sites.
- Personalization layers for recommender and assistant systems (Daily life/Software)
- What: On-device or user-specific adaptation via small iterative updates to soft prompts or adapters, improving personalization without sending all raw data to servers.
- How: Parametric or explicit amortization with small K-step updates over local usage logs; periodically refresh latents.
- Tools/workflows:
- On-Device Personalizer: background service that performs periodic mini-batch updates to soft prompts/LoRA adapters.
- Dependencies/assumptions: Efficient mobile inference; privacy controls; careful use of gradient signals (data-only updates often work well per the paper’s experiments).
- Fast cross-domain transfer for tabular/vision tasks (Education, Finance, Retail)
- What: Adapt a classifier/regressor from one domain (e.g., retailer A) to another (retailer B) using a few mini-batches; supports covariate shifts and remapped label spaces (as in MNIST↔FMNIST experiments).
- How: Implicit or explicit iterative amortization; for label remappings, explicit approaches that infer low-dimensional task latents can help interpretability.
- Tools/workflows:
- “Cold-start Adapter”: an onboarding job that runs K-step adaptation on initial batches from the new domain.
- Dependencies/assumptions: Access to initial labeled batches; domain similarity; robust monitoring for OoD behavior.
- Causal structure discovery accelerators (Academia/Science)
- What: Improve topological order prediction in causal graphs using iterative implicit amortization, as shown in the paper’s SCM results.
- How: Train rγ on diverse SCMs; at inference, refine per-graph order predictions with new observational batches.
- Tools/workflows:
- CausalMeta Toolkit: utilities to generate SCM tasks and apply iterative refinement for structure learning.
- Dependencies/assumptions: Synthetic-to-real domain gap; choice of SCM families; limited identifiability from purely observational data.
- Conditional generative modeling across related tasks (Design/Content tools)
- What: Build generators that adapt to a new target distribution from context examples (e.g., new font styles, product styles) with iterative inference of the conditional vector field (flow matching).
- How: Use the paper’s implicit iterative scheme to infer v_t(* | D) per task with K refinement steps.
- Tools/workflows:
- MetaFlow Generator: plug-in layer for diffusion/flow-based generators that conditions on examples from a new style/dataset.
- Dependencies/assumptions: Enough training tasks for meta-learning; quality of context examples; correct time-discretization for flows.
- Energy and IoT: local model adaptation for new environments (Energy/Smart devices)
- What: Quickly adapt forecasting/control models to a new building, microgrid, or device with iterative updates over recent telemetry.
- How: Parametric or explicit amortization to infer environment latents capturing device/building characteristics.
- Tools/workflows:
- Edge Adaptation Agent: periodic K-step updates on-device with privacy-preserving telemetry.
- Dependencies/assumptions: Stable data pipelines; careful control constraints (safety bounds); initial meta-training on similar assets.
- Risk and anomaly models that specialize per entity (Finance/Fraud/AIOps)
- What: Deploy per-merchant or per-service anomaly detectors that adapt iteratively as data arrives, improving accuracy and reducing false positives.
- How: Implicit amortization with streaming batches; maintain latent state per entity.
- Tools/workflows:
- Entity State Store: operational KV store keyed by entity holding current latents or logits; low-latency updates.
- Dependencies/assumptions: Strong monitoring for drift; privacy and compliance constraints; data sparsity for small entities.
Long-Term Applications
These opportunities are promising but need further research, scaling, or validation (e.g., safety, regulation, robustness under large shifts).
- General-purpose task adapters for foundation models (Cross-sector)
- What: A unified “amortization layer” that can adapt any foundation model (text, vision, speech, multimodal) to a new task via iterative mini-batch refinement, replacing many bespoke fine-tuning recipes.
- Why: The paper’s taxonomy (parametric/implicit/explicit) and iterative updates provide a blueprint; experiments show consistent gains with more steps and runtime efficiency advantages.
- Potential products: Universal Adapter Runtime that abstracts gϕ/hϕ/rγ for many backbones; automatic selection between gradient-only, data-only, or hybrid signals based on task.
- Dependencies/assumptions: Large-scale meta-training across modalities; memory/state management across queries; inference-time cost control; robust selection of amortization regime.
- Safety-critical rapid adaptation (Healthcare, Autonomous driving, Industrial control)
- What: Certified adaptation loops that update task latents/controllers online (e.g., adapting to a new hospital or road surface) with formal safety guarantees.
- How: Combine iterative amortization with verification layers, uncertainty calibration, rollback policies, and human-in-the-loop.
- Potential tools: Safety-Aware Amortizer with constraint-aware updates and formal bounds on performance degradation.
- Dependencies/assumptions: Regulatory approval; interpretable latents (parametric/explicit regimes preferred); robust OOD detection; strong offline validation sets.
- Continual/online learning with persistent memory across batches (Robotics, Edge AI)
- What: Persistent task memory that survives across sessions, enabling life-long adaptation on-device or in-robot, beyond greedy single-step objectives.
- How: Extend greedy single-step training to multi-step credit assignment (RL/evolutionary strategies, as suggested by the paper), richer memory architectures, and non-Markovian state when useful.
- Potential tools: Memory-Augmented Amortizers (episodic + parametric memory); policy selection learned over histories.
- Dependencies/assumptions: Reliable long-horizon training methods; catastrophic forgetting safeguards; privacy-preserving persistence.
- Simulation-based scientific inference at scale (Academia/Science)
- What: Parametric amortization to infer interpretable simulator parameters (e.g., physical constants, epidemiological parameters) via iterative updates on observations and gradients from differentiable simulators.
- Why: The framework unifies learned optimizers and hypernetworks; supports gradient- and data-driven signals.
- Potential products: “Amortized SBI” suite for physics, climate, neuroscience; hybrid gradient/data inference for non-invertible mappings.
- Dependencies/assumptions: Differentiable or surrogate simulators; coverage of task families; robust uncertainty quantification.
- Cross-organization federated amortized learning (Policy, Healthcare, Finance)
- What: Federated versions of gϕ/fγ that learn to adapt from distributed mini-batches without centralizing raw data, enabling privacy-preserving rapid adaptation across institutions.
- How: Federated meta-training; exchange of model deltas or latents; secure aggregation.
- Potential products: Federated Iterative Adapter (FIA) for hospitals/banks/public agencies.
- Dependencies/assumptions: FL infrastructure; privacy budgets; domain harmonization; communication-efficient state updates.
- Meta-controllers for adaptive robotics and sim-to-real transfer (Robotics)
- What: Controllers that amortize across families of dynamics and iteratively infer task latents (e.g., friction, payload) on the fly.
- Why: Paper shows parametric/explicit regimes can infer low-dimensional, interpretable latents; iterative updates scale to longer interaction sequences.
- Potential tools: Task-Latent Controllers with safety envelopes and reset/rollback strategies.
- Dependencies/assumptions: Safe exploration; real-time constraints; reliable simulators and domain randomization for meta-training.
- Retrieval-augmented generation (RAG) with adaptive evidence aggregation (Software/NLP)
- What: Iterative re-weighting and aggregation of large evidence sets for complex queries (legal/medical/financial reports) beyond context limits, with per-query state refinement.
- How: Use implicit iterative amortization to update logits or intermediate states as more batches of evidence are processed; integrate uncertainty-aware stopping.
- Potential products: Adaptive RAG Orchestrator with batch scheduling and confidence thresholds.
- Dependencies/assumptions: High-quality retrieval; latency constraints; hallucination controls.
- Adaptive energy/grid control under nonstationarity (Energy)
- What: Controllers that iteratively update environment latents to handle seasonal shifts, equipment changes, and anomalies across sites.
- How: Explicit amortization with low-dimensional task latents; combine with model-predictive control (MPC) for safety.
- Potential tools: Amortized-MPC hybrid with fast re-identification of system parameters.
- Dependencies/assumptions: High-fidelity forecasting; safety constraints; reliable telemetry.
- Personalized education copilots that generalize across curricula (Education)
- What: Tutors that iteratively refine per-student/per-course latents from streaming interactions, adapting pedagogy and assessment.
- How: Explicit amortization to learn course-level structure (fγ) and student-level latents (gϕ), updated over sessions.
- Potential products: Course Adapter + Student Latent Manager; actionable dashboards for instructors.
- Dependencies/assumptions: Consent and privacy; bias detection; coverage of curricula in meta-training.
- Robust anomaly/fraud meta-detectors across regimes (Finance/AIOps)
- What: Meta-detectors that can adapt to new entities and shifts (e.g., new fraud patterns) with iterative updates and shared priors across merchants/services.
- How: Hybrid gradient/data signals based on availability; maintain per-entity state with decay and drift alerts.
- Potential tools: Regime-Aware Amortizer with explainability reports for auditors.
- Dependencies/assumptions: Compliance; interpretability; strong monitoring; guardrails for false alarm cascades.
Notes on choosing an amortization regime (practical guidance)
- Parametric amortization (fixed f, learned gϕ): Best when the likelihood/function class is known or constrained (simulators, interpretable linear/logistic heads), and when you can benefit from gradient access. Offers compact, interpretable task latents. Often most robust and efficient in practice per paper results.
- Implicit amortization (learned fγ, identity g): Best when flexible modeling is needed and the task can be expressed as direct conditioning on observations. Works well for ICL/RAG-like setups; iterative refinement helps scale beyond context limits.
- Explicit amortization (learn fγ and gϕ): Most expressive but harder to optimize due to non-stationarity between fγ and gϕ. Prefer when low-dimensional task latents are valuable and gradients are available; plan for extra engineering to stabilize training.
Cross-cutting assumptions and dependencies
- Meta-training data: Strong performance relies on diverse, representative task families; large domain shifts reduce gains.
- Signal choice: Gradients alone can be suboptimal in low dimensions; combining data and gradients helps, while in higher dimensions gradients can be crucial (as observed in the paper).
- Compute and latency: Iterative methods are K-times more efficient than one-step models processing the same total data (runtime O(KB2) vs O((KB)2)), but still require careful tuning of K and batch size B.
- Privacy and compliance: Many applications (healthcare, finance, public sector) require privacy-preserving meta-training and strict monitoring.
- Safety and monitoring: For safety-critical domains, pair iterative adaptation with uncertainty estimation, OOD detection, and rollback mechanisms.
- Engineering detail: Causal masking, state representation (logits often best for implicit models), and memory management across queries are critical for stable gains.
Glossary
- Amortized learning: Reusing computation or inductive biases across tasks to enable rapid generalization. "Modern learning systems increasingly rely on amortized learning — the idea of reusing computation or inductive biases shared across tasks to enable rapid generalization to novel problems."
- Back-propagation through time: A training method that unrolls recurrent computation to compute gradients across sequence steps. "back-propagation through time \citep{ha2016hypernetworks}"
- Causal discovery: Inferring causal relationships or graph structure from data. "implicit models recover algorithmic behaviors such as gradient descent or causal discovery."
- Causal masking: Attention masking that enforces causal (temporal/order-based) constraints in sequence models. "All three frameworks — parametric, explicit and implicit — modify causal masking to provide efficient and parallelizable computation of and with mini-batches having varied number of observations"
- Conditional neural processes: Models that learn predictive distributions conditioned on context data via learned embeddings. "implicit amortization, which subsumes in-context learning and specific cases of prior fitted networks and conditional neural processes"
- Conditional predictive distribution: The distribution of outputs given inputs and task-specific context data. "Certain meta-learning methods like example-based in-context learning or prior fitted networks instead directly model the conditional predictive distribution"
- Conditional vector field: A learned vector field defining transport dynamics conditioned on task data. "We apply the flow-matching framework ... to learn the conditional vector field given task data , and evaluate samples generated conditioned on novel densities as context unseen during training."
- DINO-v2: A self-supervised vision foundation model used for image embeddings. "The images are embedded using Dino-v2 \citep{oquab2023dinov2} before feeding to the transformer."
- Empirical risk minimization (ERM): Minimizing average loss over a dataset to approximate true risk minimization. "which is often accomplished by empirical risk minimization"
- Evolutionary strategies: Black-box optimization methods inspired by evolution, used to optimize learning procedures. "evolutionary strategies \citep{metz2022velo} depending on the form of "
- Explicit amortization: A regime that disentangles generalization and adaptation by learning both dataset-level embeddings and task-conditioned predictors. "explicit amortization which disentangles generalization and local adaptation by learning both a dataset-level embedding and a task-conditioned prediction function"
- Flow-matching framework: A methodology for generative modeling that learns transport via vector fields. "We apply the flow-matching framework \citep{lipman2022flow, tong2023conditional, albergo2023stochastic} to learn the conditional vector field given task data "
- Hypernetworks: Networks that generate parameters (e.g., weights) for another network conditioned on input/task signals. "hypernetworks \citep{li2021prefix,ha2016hypernetworks,gaier2019weight,jia2016dynamic,munkhdalai2017meta} and learned optimizers instead directly model task-specific parameters as outputs of a learned process"
- In-Context Learning (ICL): Performing task adaptation at inference by conditioning on example observations or instructions. "In-Context Learning when samples a set of observations and is modeled as a predictive sequence model with the context as observations."
- Inductive bias: Assumptions encoded in a model that guide learning across tasks. "the shared inductive bias (e.g., the equations of motion) is amortized across tasks, enabling fast, local, and sample-efficient adaptation."
- Iterative Amortized Inference: A class of models that refine solutions step-by-step over mini-batches for scalable adaptation. "Iterative Amortized Inference for parametric, explicit and implicit parameterizations."
- LLMs: Large-scale pretrained sequence models that enable adaptation via context conditioning. "amortization is implicitly incentivized in LLMs by training on diverse contexts"
- Learned optimizers: Models that learn to produce parameter updates (e.g., from gradients) instead of hand-designed optimization rules. "Learned optimizers instead amortize optimization itself, learning to predict parameter updates of fixed models conditioned on gradients."
- Markovian: An update process where the next state depends only on the current state, not the full history. "Note that this iterative refinement is Markovian"
- Meta-learning: Learning to learn across tasks by extracting transferrable knowledge for rapid adaptation. "including meta-learning, in-context learning, prompt tuning, learned optimizers and more."
- Mixture of Gaussian (MoG): A probabilistic model representing data as a mixture of multiple Gaussian components. "Mixture of Gaussian (MoG) Generation."
- Model-Agnostic Meta-Learning (MAML): A meta-learning method that learns an initialization enabling fast fine-tuning on new tasks. "Traditional meta-learning approaches e.g. Model-Agnostic Meta-Learning \citep[MAML;] []{finn2017model} alleviate this problem by learning global initialization parameters "
- Non Markovian: An update process that depends on multiple past states or an augmented history. "A system is Markovian if it only relies on the current or non Markovian if on more past states."
- Non-stationarity: A learning scenario where the data-generating or optimization dynamics change over time/joint training. "inherent non-stationarity during learning — and are dependent on each other but have to be learned together."
- Out-of-Distribution (OoD): Evaluation on tasks or data that differ from those seen during training. "OoD settings where models are trained on MNIST and evaluated on FashionMNIST, and vice versa."
- Parametric amortization: A regime where a learned function maps task data to parameters of a fixed model. "Parametric. We define the class of amortized models with a fixed and learnable as parametric amortization."
- Posterior distribution: The distribution over latent parameters given observed data. "Several works ... approximate the posterior distribution over parameters of the likelihood as "
- Posterior predictive distribution: The distribution of future observations given past data, integrating over parameter uncertainty. "apart from the broader perspective of learning the posterior predictive distribution"
- Prior Fitted Networks (PFNs): Models trained to approximate Bayesian inference and predictive distributions conditioned on context. "Prior Fitted Networks (PFNs) or ICL \citep{brown2020language,dong2022survey,garg2022can,von2023transformers,hollmann2022tabpfn}"
- Prompt tuning: Adapting models via learned prompts or instructions rather than updating all model weights. "including meta-learning, in-context learning, prompt tuning, learned optimizers and more."
- Soft prompts: Learnable embedding tokens used to condition models without changing backbone weights. "soft prompts, latent states, or context tokens"
- Stochastic gradient descent (SGD): An iterative optimizer that updates parameters using gradients computed on mini-batches. "most commonly stochastic gradient descent"
- Stochastic optimization: Optimization methods that use random subsets of data (mini-batches) to scale learning. "drawing inspiration from stochastic optimization."
- Structural causal model (SCM): A formal causal framework defining variables and their causal mechanisms/graph structure. "each task involves sampling a structural causal model (SCM) and inferring its topological order using only observational data."
- Topological order: An ordering of nodes in a DAG consistent with causal/acyclic dependencies. "inferring its topological order using only observational data."
- Transformer: A sequence model using attention mechanisms for conditioning on context and queries. " is a recurrent application of a transformer with weights "
- Wasserstein distance: A metric for comparing probability distributions based on optimal transport. "for generative modeling problems we consider the 2-Wasserstein () and 1-Wasserstein () distance between samples from the true and generated distribution."
Collections
Sign up for free to add this paper to one or more collections.