Applying non-negative matrix factorization with covariates to label matrix for classification (2510.10375v1)

Abstract: Non-negative matrix factorization (NMF) is widely used for dimensionality reduction and interpretable analysis, but standard formulations are unsupervised and cannot directly exploit class labels. Existing supervised or semi-supervised extensions usually incorporate labels only via penalties or graph constraints, still requiring an external classifier. We propose \textit{NMF-LAB} (Non-negative Matrix Factorization for Label Matrix), which redefines classification as the inverse problem of non-negative matrix tri-factorization (tri-NMF). Unlike joint NMF methods, which reconstruct both features and labels, NMF-LAB directly factorizes the label matrix $Y$ as the observation, while covariates $A$ are treated as given explanatory variables. This yields a direct probabilistic mapping from covariates to labels, distinguishing our method from label-matrix factorization approaches that mainly model label correlations or impute missing labels. Our inversion offers two key advantages: (i) class-membership probabilities are obtained directly from the factorization without a separate classifier, and (ii) covariates, including kernel-based similarities, can be seamlessly integrated to generalize predictions to unseen samples. In addition, unlabeled data can be encoded as uniform distributions, supporting semi-supervised learning. Experiments on diverse datasets, from small-scale benchmarks to the large-scale MNIST dataset, demonstrate that NMF-LAB achieves competitive predictive accuracy, robustness to noisy or incomplete labels, and scalability to high-dimensional problems, while preserving interpretability. By unifying regression and classification within the tri-NMF framework, NMF-LAB provides a novel, probabilistic, and scalable approach to modern classification tasks.

• The paper introduces NMF-LAB, a novel framework that inverts traditional NMF by directly factorizing the label matrix with covariates, unifying regression and classification.
• It employs kernel-based covariates and multiplicative update rules to achieve competitive accuracy and robustness to label noise, as demonstrated on datasets like MNIST.
• The framework offers a trade-off between high interpretability with linear models and superior predictive performance using kernel methods, scaling via Nyström approximation.

Non-negative Matrix Factorization with Covariates for Direct Label Matrix Factorization in Classification

Introduction and Motivation

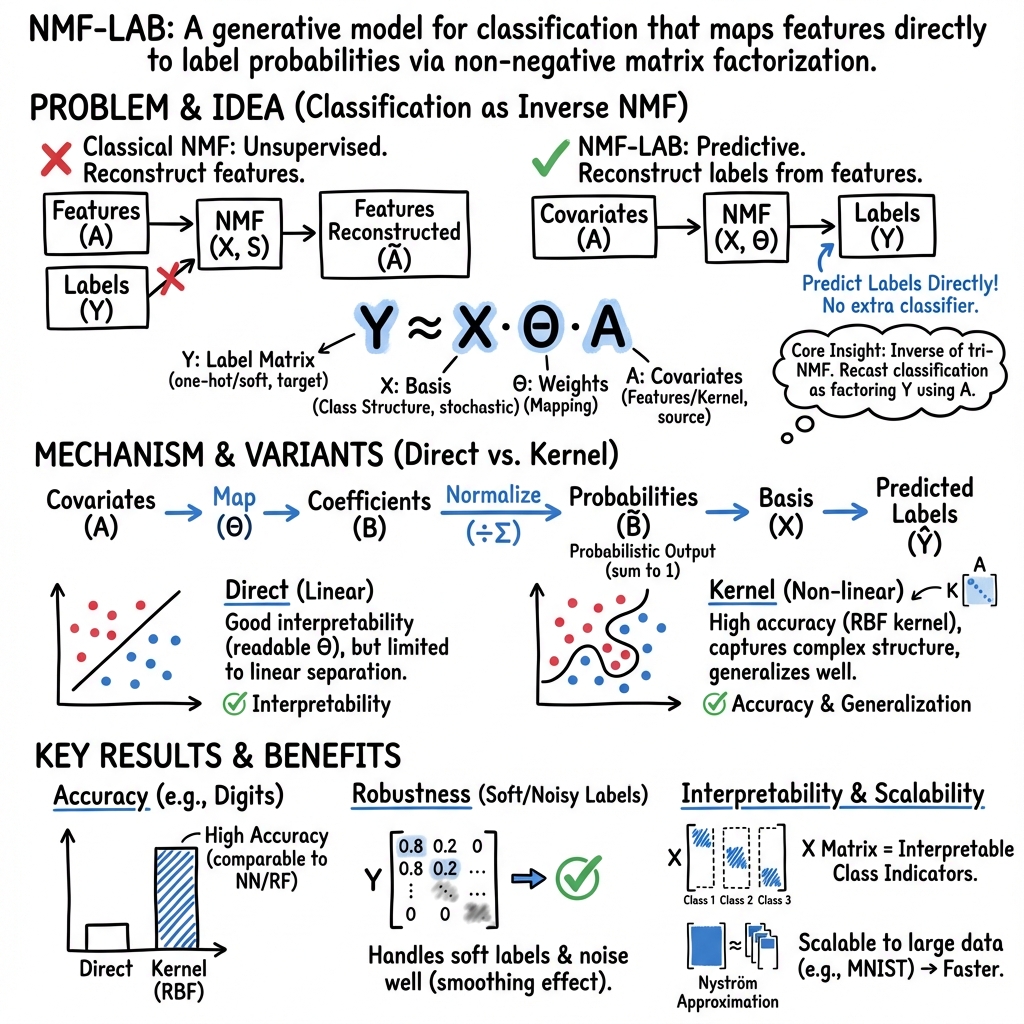
This paper introduces NMF-LAB, a novel framework that recasts classification as the inverse problem of non-negative matrix tri-factorization (tri-NMF), directly factorizing the label matrix with covariates. Unlike prior supervised or semi-supervised NMF extensions, which typically incorporate label information via auxiliary penalties or constraints and require an external classifier, NMF-LAB treats the label matrix as the primary observation and covariates as explanatory variables. This inversion enables direct estimation of class-membership probabilities and seamless integration of covariates—including kernel-based similarities—for generalization to unseen samples. The approach unifies regression and classification within a single tri-NMF framework, offering both interpretability and scalability.

Theoretical Framework

Tri-NMF and Forward–Inverse Duality

The classical NMF with covariates (forward problem) approximates an observation matrix $Y$ as $Y \approx X \Theta A$, where $X$ and $\Theta$ are non-negative matrices to be learned, and $A$ is a known covariate matrix. In the forward setting, $Y$ typically represents features, and $A$ encodes covariates, enabling regression-type tasks.

NMF-LAB inverts this relationship: the label matrix $Y$ (one-hot encoded) is the observation, and $A$ contains covariates. The factorization $Y \approx X \Theta A$ is optimized such that $X$ (with columns normalized to sum to one) aligns with class indicators, and the coefficients $B = \Theta A$ (normalized) yield class-membership probabilities. This inversion provides a direct probabilistic mapping from covariates to labels, eliminating the need for a separate classifier.

Probabilistic Interpretation and Identifiability

By normalizing the columns of $X$ and $B$, the reconstructed matrix $\tilde{Y} = X \tilde{B}$ provides class-membership probability vectors for each sample. When the number of bases equals the number of classes ($Q = P$), the columns of $X$ often approximate one-hot vectors, aligning with class structure. This property is supported by recent results on partial identifiability in NMF, which guarantee that, under mild conditions, a subset of latent factors can be reliably identified up to permutation and scaling.

Kernel-based Covariates

To capture nonlinear relationships, NMF-LAB supports kernel-based covariates. The Gaussian (RBF) kernel is used to construct $A$, with the kernel parameter $\beta$ optimized via cross-validation. The representer theorem justifies this approach, ensuring that the solution can be expressed as a linear combination of kernel functions evaluated at training points. For large-scale data, the Nyström approximation is employed to reduce the computational complexity of kernel matrix operations.

Implementation and Optimization

Multiplicative Updates

Optimization is performed using multiplicative update rules derived from the tri-NMF objective, ensuring monotonic decrease of the squared Euclidean loss. After each update, columns of $X$ are normalized to sum to one, maintaining probabilistic interpretability. Initialization is critical due to non-convexity; for classification, initializing $X$ as the identity matrix (or using K-means centroids) aligns basis vectors with class labels and accelerates convergence.

Semi-supervised Learning

NMF-LAB naturally extends to semi-supervised settings by encoding unlabeled samples as uniform distributions over classes in $Y$. The factorization process smooths over label noise and missing labels, providing robustness in partially labeled scenarios.

Empirical Evaluation

Predictive Performance

Experiments on diverse datasets (RBGlass1, Iris, Penguins, Wine, Seeds, Vehicle, Digits, MNIST) demonstrate that:

• NMF-LAB (kernel) achieves predictive accuracy comparable to state-of-the-art classifiers (NN, RF, SVM, KNN), especially on non-linearly separable data.
• NMF-LAB (direct) (linear model) is competitive only when the data are linearly separable, but offers superior interpretability.
• On MNIST, NMF-LAB (kernel) with Nyström approximation achieves 93.7% accuracy (1000 landmarks), approaching the full kernel model (96.0%) and Random Forest (95.8%).

Robustness to Label Noise

NMF-LAB exhibits robustness to label noise due to the smoothing effect of matrix factorization. In experiments with soft labels, NMF-LAB (kernel) maintains high accuracy as the proportion of correct label information increases, outperforming joint NMF (SSNMF) and matching or exceeding neural networks under moderate noise.

Interpretability

The linear variant, NMF-LAB (direct), provides direct, non-negative, and additive contributions of features to class probabilities. For example, in the RBGlass1 dataset, the parameter matrix $\Theta$ reveals which features (e.g., Fe, P, Mn) drive class membership, supporting transparent, parts-based interpretation. However, this interpretability comes at the cost of reduced predictive power on complex datasets.

Scalability

The Nyström approximation enables NMF-LAB (kernel) to scale to large datasets (e.g., MNIST with 60,000 samples), reducing kernel matrix computation from $O(N^2)$ to $O(NM)$, where $M$ is the number of landmarks. Landmark selection via K-means centroids provides both theoretical and empirical accuracy guarantees.

Trade-offs and Limitations

A central finding is the trade-off between interpretability and predictive accuracy:

• NMF-LAB (direct): High interpretability, limited to linearly separable problems.
• NMF-LAB (kernel): High predictive accuracy, reduced feature-level interpretability.

The method is robust to label noise and missing labels, but the non-convexity of the objective function means only local optima are guaranteed. The framework currently relies on squared Euclidean loss; extensions to other divergences (e.g., KL) are possible. Scalability to extremely high-dimensional features may require further approximation techniques (e.g., random features).

Implications and Future Directions

NMF-LAB provides a unified, probabilistic, and interpretable framework for classification, bridging regression and classification via the forward–inverse duality of tri-NMF. Its direct mapping from covariates to label probabilities, robustness to label noise, and scalability make it suitable for modern supervised and semi-supervised learning tasks.

Future research directions include:

• Extending to multi-label learning and settings with missing labels.
• Developing compact representations with fewer bases than classes ($Q < P$).
• Exploring alternative loss functions and deep feature extraction as covariates.
• Integrating with dynamic models (e.g., NMF-VAR) for time series and sequential data.

Conclusion

NMF-LAB reframes classification as the inverse problem of tri-NMF, enabling direct, probabilistic mapping from covariates to labels without external classifiers. The framework achieves a favorable balance between interpretability and predictive accuracy, is robust to label noise, and scales to large datasets via kernel approximation. By establishing a duality between regression and classification within the tri-NMF framework, NMF-LAB offers both theoretical insight and practical utility for supervised learning. Future work will further explore its extensions to multi-label, dynamic, and high-dimensional settings.