The Algorithmic Regulator (2510.10300v3)

Abstract: The regulator theorem states that, under certain conditions, any optimal controller must embody a model of the system it regulates, grounding the idea that controllers embed, explicitly or implicitly, internal models of the controlled. This principle underpins neuroscience and predictive brain theories like the Free-Energy Principle or Kolmogorov/Algorithmic Agent theory. However, the theorem is only proven in limited settings. Here, we treat the deterministic, closed, coupled world-regulator system $(W,R)$ as a single self-delimiting program $p$ via a constant-size wrapper that produces the world output string~$x$ fed to the regulator. We analyze regulation from the viewpoint of the algorithmic complexity of the output, $K(x)$. We define $R$ to be a \emph{good algorithmic regulator} if it \emph{reduces} the algorithmic complexity of the readout relative to a null (unregulated) baseline $\varnothing$, i.e., [ Δ= K\big(O_{W,\varnothing}\big) - K\big(O_{W,R}\big) > 0. ] We then prove that the larger $Δ$ is, the more world-regulator pairs with high mutual algorithmic information are favored. More precisely, a complexity gap $Δ> 0$ yields [ \Pr\big((W,R)\mid x\big) \le C\,2^{\,M(W{:}R)}\,2^{-Δ}, ] making low $M(W{:}R)$ exponentially unlikely as $Δ$ grows. This is an AIT version of the idea that ``the regulator contains a model of the world.'' The framework is distribution-free, applies to individual sequences, and complements the Internal Model Principle. Beyond this necessity claim, the same coding-theorem calculus singles out a \emph{canonical scalar objective} and implicates a \emph{planner}. On the realized episode, a regulator behaves \emph{as if} it minimized the conditional description length of the readout.

• The paper shows that regulators reduce algorithmic complexity by compressing system outputs to model their environments.
• It introduces a complexity gap metric (Δ = K(O_none) – K(O_reg)) to quantify effective regulation via output compressibility.
• The work formalizes regulator theorems using probabilistic methods, highlighting mutual algorithmic information as a basis for robust control.

The Algorithmic Regulator

Introduction

The paper "The Algorithmic Regulator" (2510.10300) explores the theoretical underpinnings and implications of the regulator theorem using algorithmic information theory (AIT). The authors aim to extend the concept that optimal controllers embody models of the systems they regulate by examining complexity from an algorithmic perspective. Through this lens, regulation is considered a form of compression, where the algorithmic complexity of the system's output is reduced under the influence of a regulator.

This paper innovatively treats the deterministic world-regulator system $(W, R)$ as a self-delimiting program, proposing a definition of a "good algorithmic regulator" as one that reduces the algorithmic complexity of its readout compared to an unregulated baseline. The findings reveal that the greater this reduction, the more likely pairs of world and regulator with high mutual algorithmic information are favored, quantifying the notion that a regulator contains a model of the world.

Model Definition and Analysis

The foundational aspect of this research is defining a model in terms of algorithmic information and demonstrating how regulators embody these models. The paper defines a regulator as carrying a model of the world if there is algorithmic mutual information between the two, expressed as $M(W{:}R) > 0$. This indicates that the regulator contains algorithmic structure relevant to the world it regulates.

The authors employ the framework of algorithmic information theory to measure mutual algorithmic information $M(W{:}R)$, providing a more rigorous grounding than traditional approaches, which often lack precise definitions. This measure is pivotal as it quantifies the shared structure between $W$ and $R$ and highlights the connections between this shared information and effective regulation.

Regulation as Compression

A critical contribution of the paper is the notion of regulation as compression. By scoring a regulator based on the compressibility of its output error stream, the authors link effective regulation directly to algorithmic simplicity. The paper demonstrates how regulators can be assessed by comparing the description length of outputs given a regulator versus a baseline with no regulation.

The strength of the regulator is dictated by the complexity gap $\Delta = K(O_{W,\varnothing}) - K(O_{W,R})$, where $O_{W,\varnothing}$ is the complexity without regulation, and $O_{W,R}$ represents complexity when regulated. Larger gaps suggest that the regulator embodies a model of the world, thus favoring configurations where mutual information is high.

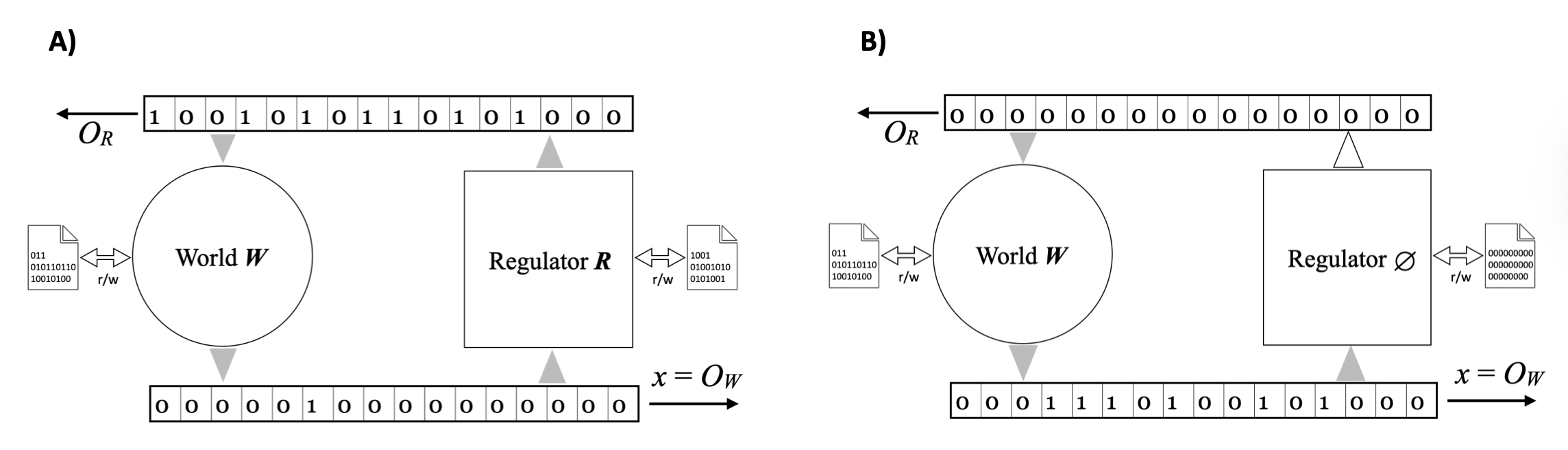
Figure 1: A good regulator $R$ interacts with the world $W$ so that the readout $x = O_W$ is clamped to a simple, highly compressible sequence.

Probabilistic Regulator Theorems

The paper proposes several theorems to formalize and prove the relationships between regulation, model embodiment, and algorithmic information. Particularly, the probabilistic regulator theorem establishes a bound on the probability of a world-regulator pair given an observed regulated output, showing how the complexity gap $\Delta$ penalizes configurations lacking mutual information.

The probabilistic approach underscores the idea that regulation in the algorithmic sense aligns world $W$ and regulator $R$ through information-sharing processes, emphasizing the regulator's role in making the system's responses predictable and compressible.

Implications and Future Directions

The implications of this research are profound, suggesting that algorithmic information theory provides a robust framework for understanding control and regulation systems beyond classical assumptions of linearity and specific signal classes. This model offers compelling insights into the architectural requirements for creating regulators that inherently model their environments, facilitating applications not only in engineered systems but also potentially in biological and cognitive domains.

Future research may expand on this work by exploring distributed systems, non-linear dynamics, and hybrid models, applying the principles of algorithmic information theory to broader classes of control systems. Furthermore, the intersection of these ideas with fields like artificial intelligence and neuroscience could yield fruitful advancements in understanding adaptive, intelligent regulation in complex environments.

Conclusion

This paper successfully translates the intuitive concept that regulators model systems into precise mathematical formulations using algorithmic information theory. By grounding regulation in compressibility and demonstrating how mutual algorithmic information is favored, the authors provide a new lens through which effective regulation can be understood and developed. The insights gained have the potential to redefine approaches to control systems across disciplines, opening new pathways for innovation and application.