Multi-Robot Distributed Optimization for Exploration and Mapping of Unknown Environments using Bioinspired Tactile-Sensor (2510.06085v1)

Abstract: This project proposes a bioinspired multi-robot system using Distributed Optimization for efficient exploration and mapping of unknown environments. Each robot explores its environment and creates a map, which is afterwards put together to form a global 2D map of the environment. Inspired by wall-following behaviors, each robot autonomously explores its neighborhood based on a tactile sensor, similar to the antenna of a cockroach, mounted on the surface of the robot. Instead of avoiding obstacles, robots log collision points when they touch obstacles. This decentralized control strategy ensures effective task allocation and efficient exploration of unknown terrains, with applications in search and rescue, industrial inspection, and environmental monitoring. The approach was validated through experiments using e-puck robots in a simulated 1.5 x 1.5 m environment with three obstacles. The results demonstrated the system's effectiveness in achieving high coverage, minimizing collisions, and constructing accurate 2D maps.

• The paper introduces a decentralized multi-robot system that uses tactile sensing inspired by cockroach antennae to efficiently navigate unknown environments.
• The methodology optimizes collision avoidance and exploration through distributed optimization with tuned parameters (β = 0.9, γ = 0.1) and scalable robot coordination.
• Experimental results demonstrate effective mapping and robust performance in cluttered scenarios, with seven robots yielding optimal exploration efficiency.

Multi-Robot Distributed Optimization with Bioinspired Tactile-Sensors

Introduction

Exploration and mapping of unknown environments pose significant challenges, particularly in applications such as search-and-rescue, industrial inspection, and environmental monitoring. The paper introduces a decentralized multi-robot system inspired by cockroach antennae, designed for efficient exploration using tactile sensing. Unlike traditional optical sensors like LiDAR and cameras that struggle in challenging environments (e.g., with transparent surfaces or adverse weather conditions), the proposed system utilizes tactile sensors to log collision points with obstacles, thus facilitating robust navigation in cluttered spaces.

Proposed System and Methodology

System Design

The proposed system employs e-puck robots equipped with rangefinder sensors that emulate tactile feedback by logging collision points instead of avoiding obstacles. Each robot autonomously explores its vicinity, generates local maps, and aggregates these maps into a comprehensive global representation of the environment.

Figure 1: Multi-Robot Exploration of an Unknown Environment: The magenta circle represents each robot's communication radius, the red circle shows its sensing range for obstacle detection, and the green circles are candidate goal points. The green arrow indicates the selected trajectory. Robots detecting blue obstacles move backward and choose a new goal.

Navigation and Coordination

The robots navigate using a decentralized control strategy optimized via distributed optimization:

• Goal Generation: Robots generate candidate trajectories based on their current position and tactically select the trajectory that minimizes the cost function comprising collision and redundancy penalties.
• Cost Function: Defined by $$J_i(\mathbf{g}_k) = \beta J_{\text{collision}} + \gamma J_{\text{redundancy}}$$, where $\beta$ and $\gamma$ dictate the collision avoidance and exploration emphasis respectively.
• Algorithm: The system iteratively updates robot positions based on chosen trajectories until a predefined number of obstacle points are logged.

  Figure 2: Left: The e-puck robot used in the experiments. Right: Top view of the e-puck showing the distribution of rangefinder sensors (ps0-ps7) used for obstacle detection.

Experimental Evaluation

Parameter Tuning

The experiments initiated with varying $\beta$ and $\gamma$ parameters to balance collision avoidance with exploration efficiency. Results demonstrated $\beta = 0.9$ and $\gamma = 0.1$ as optimal values, maximizing logged points while successfully minimizing collisions.

Figure 3: Robot movement in the 3 robot simulation with the best weighting parameters ($\beta = 0.9$ and $\gamma = 0.1$). It can be observed that the robots tend to stay at the borders of the environment, based on the high collision avoidance priority given.

Scalability Analysis

The approach accommodates different robot numbers, confirming seven robots as optimal for rapid and effective mapping in a constrained environment. Increasing robot numbers benefits exploration rate but introduces computational challenges and geometrical constraints limiting further scalability.

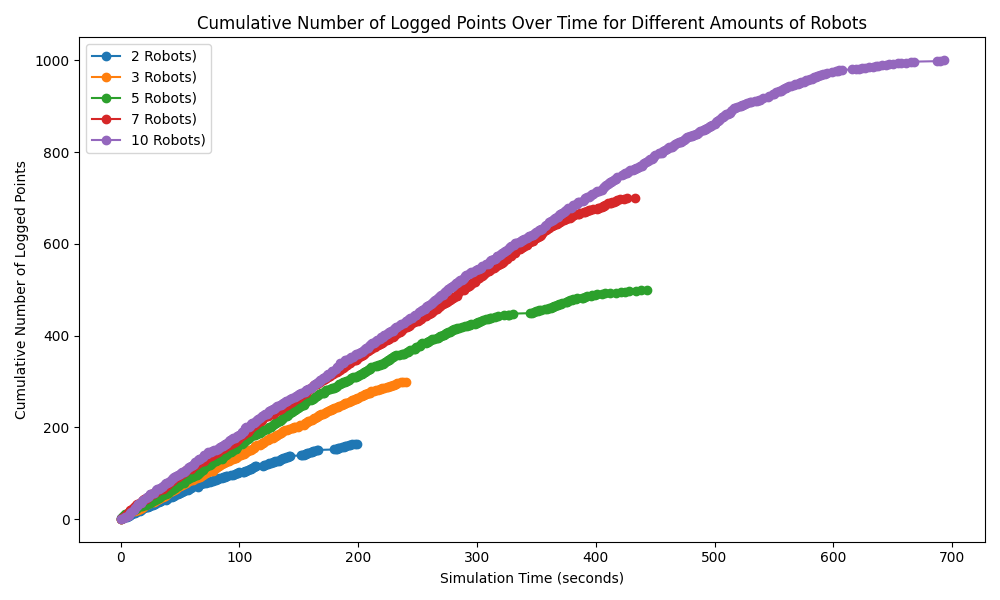
Figure 4: Logged points over time for simulations with different amounts of robots.

Communication Constraints

The impact of communication limitations was assessed by varying the maximum communication range. Reduced communication distances incurred higher collision rates and longer exploration times but facilitated denser mapping in focused areas.

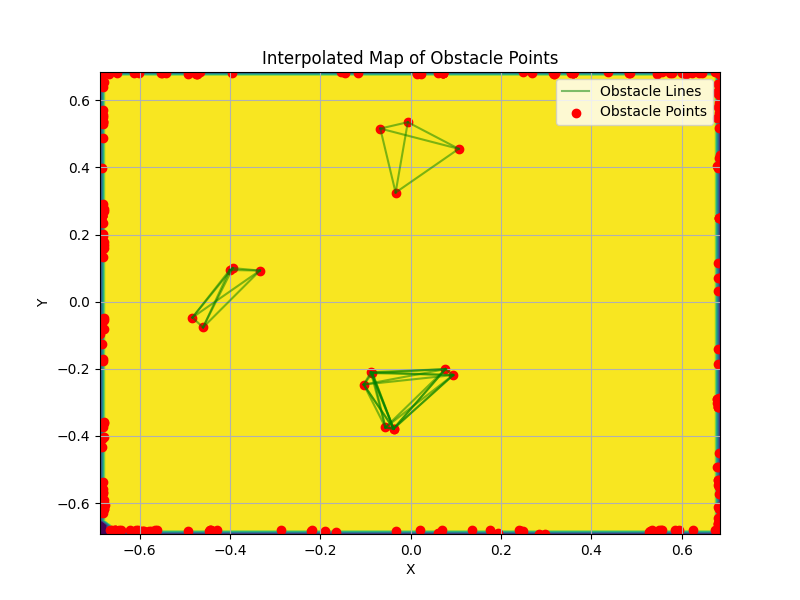
Figure 5: Interpolated map from the logged obstacle points from the 10 robots simulation with $\beta = 0.9$ and $\gamma = 0.1$.

Conclusion and Future Work

The system effectively demonstrated robust exploration capabilities under various configurations, facilitating reliable mapping in challenging environments. Optimization of collision avoidance and exploration was critical, validating the decentralized system's scalability and efficiency.

Future research will explore larger, more obstacle-rich environments, real-world deployment with tactile sensors, and advanced strategies to address dynamic obstacles and optimal energy utilization. Incorporating machine learning for adaptive decision-making in changing scenarios remains prospective for refinement.

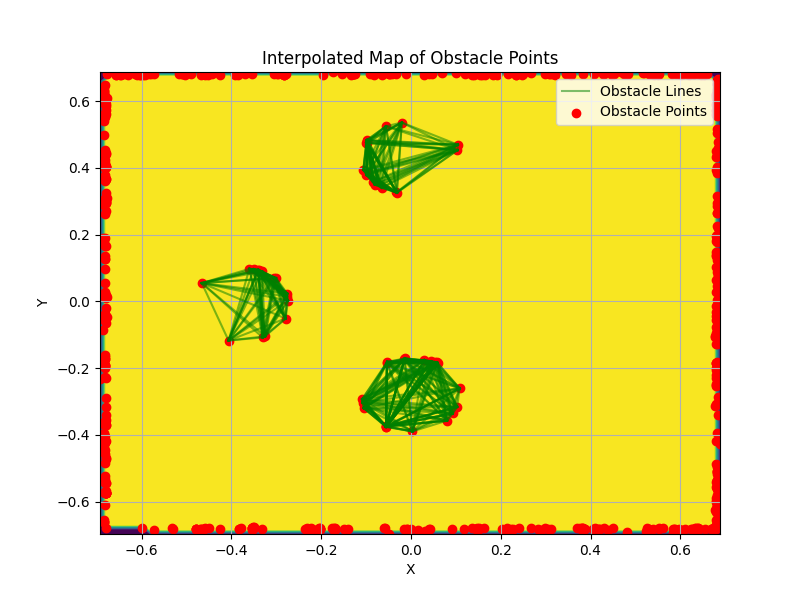
Figure 6: Interpolated map from the logged obstacle points in the 7-robot simulation with communication constraints ($r_{\text{comm} = 0.5~\text{m}$).