NorMuon: Making Muon more efficient and scalable (2510.05491v1)
Abstract: The choice of optimizer significantly impacts the training efficiency and computational costs of LLMs. Recently, the Muon optimizer has demonstrated promising results by orthogonalizing parameter updates, improving optimization geometry through better conditioning. Despite Muon's emergence as a candidate successor to Adam, the potential for jointly leveraging their strengths has not been systematically explored. In this work, we bridge this gap by proposing NorMuon (Neuron-wise Normalized Muon), an optimizer that synergistically combines orthogonalization with neuron-level adaptive learning rates. Our analysis reveals that while Muon effectively reduces condition numbers, the resulting updates exhibit highly non-uniform neuron norms, causing certain neurons to dominate the optimization process. NorMuon addresses this imbalance by maintaining second-order momentum statistics for each neuron and applying row-wise normalization after orthogonalization, ensuring balanced parameter utilization while preserving Muon's conditioning benefits. To enable practical deployment at scale, we develop an efficient distributed implementation under the FSDP2 framework that strategically distributes orthogonalization computations across devices. Experiments across multiple model scales demonstrate that NorMuon consistently outperforms both Adam and Muon, achieving 21.74% better training efficiency than Adam and 11.31% improvement over Muon on 1.1 B pretraining setting, while maintaining a comparable memory footprint to Muon. Our findings suggest that orthogonalization and adaptive learning rates are complementary rather than competing approaches, opening new avenues for optimizer design in large-scale deep learning.
Summary
- The paper demonstrates that integrating orthogonalization with neuron-wise adaptive learning rates significantly improves convergence efficiency and balance in large-scale LLM training.
- It introduces a distributed FSDP2-compatible implementation that minimizes communication overhead while maintaining memory efficiency for models up to 5.4B parameters.
- Empirical results reveal a 21.74% reduction in training steps over AdamW, confirming the benefits of combining geometric preconditioning with adaptive neuron normalization.
NorMuon: Integrating Orthogonalization and Neuron-wise Adaptivity for Efficient and Scalable LLM Optimization
Introduction
The NorMuon optimizer addresses a central challenge in LLM training: achieving both efficient convergence and scalable memory/computation profiles through improved optimization geometry. Building on the Muon optimizer, which orthogonalizes parameter updates to improve conditioning, NorMuon introduces neuron-wise adaptive learning rates to correct the high variance in per-neuron update norms observed in Muon. This combination is shown to yield more balanced parameter utilization and superior training efficiency, with a distributed implementation that is practical for large-scale deployments.
Motivation and Analysis of Optimization Geometry
The paper begins by analyzing the update directions of various optimizers during LLM pretraining, focusing on two axes: the singular value spectrum of update matrices (reflecting conditioning) and the variance of per-neuron update norms (reflecting parameter utilization). Muon’s orthogonalization step effectively reduces the condition number of updates, as evidenced by a more uniform singular value distribution compared to AdamW and raw momentum.
Figure 1: Singular value (sorted) of update directions, demonstrating Muon's improved conditioning over AdamW and momentum.
However, Muon’s updates exhibit high variance in per-neuron norms, leading to imbalanced learning dynamics where certain neurons dominate the optimization process. In contrast, AdamW achieves more uniform per-neuron update norms but does not address conditioning as effectively.
This motivates the core insight: orthogonalization and adaptive learning rates are not mutually exclusive but can be complementary. NorMuon is designed to combine Muon’s conditioning benefits with neuron-wise normalization to ensure balanced parameter updates.
NorMuon Algorithm
NorMuon augments Muon’s orthogonalization with a neuron-wise adaptive learning rate mechanism. The optimizer maintains:
- A first-order momentum matrix (as in Muon).
- A per-neuron (row-wise) second-order momentum vector, tracking the mean squared update magnitude for each neuron.
The update procedure is as follows:
- Momentum Update: Compute the first-order momentum as an exponential moving average of gradients.
- Orthogonalization: Apply the Newton-Schulz (NS5) iteration to approximate the orthogonal polar factor of the momentum matrix.
- Neuron-wise Normalization: Compute the mean squared value across columns for each row (neuron) of the orthogonalized update, accumulate this into the second-order momentum, and normalize each row accordingly.
- Learning Rate Scaling: Rescale the update to match the RMS norm of Adam, ensuring stable step sizes.
- Parameter Update: Apply the normalized, orthogonalized update with decoupled weight decay.
This approach ensures that the optimizer benefits from both improved conditioning (via orthogonalization) and balanced parameter utilization (via neuron-wise normalization).
Distributed Implementation
Scaling NorMuon to large models necessitates an efficient distributed implementation. The authors develop a strategy compatible with the FSDP2 framework, which shards parameters and optimizer states across devices. Key features include:
- Orthogonalization Distribution: Parameters are sorted by size and assigned to devices in a round-robin fashion. Each device gathers the full momentum matrix for its assigned parameters, performs orthogonalization, and scatters the result back, eliminating redundant computation.
- Shard-local Row Normalization: FSDP2’s row-wise sharding allows neuron-wise normalization to be performed locally on each device, avoiding additional communication.
This design achieves optimal memory efficiency and manageable communication overhead, with only a modest increase in per-iteration latency compared to AdamW.
Empirical Results
Large-Scale Pretraining
Experiments on 1.1B and 5.4B parameter Transformers pretrained on SlimPajama demonstrate that NorMuon consistently outperforms AdamW, Muon, and Dion. NorMuon achieves a 21.74% reduction in training steps over AdamW and an 11.31% improvement over Muon for the 1.1B model, with similar trends at larger scales.
Figure 2: Pretraining results of 1.1B model, showing NorMuon's superior convergence compared to AdamW, Muon, and Dion.
Figure 3: Validation loss vs wallclock time on 5.4B pretraining experiments, indicating NorMuon's efficiency advantage.
Ablation Studies
Ablations confirm that:
- Neuron-wise normalization after orthogonalization is superior to coordinate-wise normalization or normalization before orthogonalization.
- Applying normalization to all matrices (not just those with ) is beneficial, even when the matrix is full-rank and theoretically orthogonalizable.
Figure 4: Ablation studies of NorMuon on 1.1B pretraining experiments, highlighting the importance of neuron-wise normalization after orthogonalization.
Small-Scale Pretraining
On 124M and 350M parameter Modded-NanoGPT models, NorMuon outperforms Muon, with the efficiency gap increasing with model size (6% for 124M, 15% for 350M).
Figure 5: Pretraining results of 124M model, showing NorMuon's consistent improvement over Muon.
Figure 6: Ablation studies on pretraining 350M model, further validating NorMuon's design choices.
Overhead and Scalability
NorMuon maintains Muon’s memory efficiency, requiring only a negligible increase in memory for the per-neuron statistics. The communication overhead is moderate (33–50% increase depending on precision), but can be overlapped with computation. The optimizer step time increases by only 2.9% compared to AdamW, and the overall training step time remains within 3% of AdamW, validating the practicality of the approach for large-scale distributed training.
Theoretical and Practical Implications
NorMuon demonstrates that orthogonalization and adaptive learning rates are not competing paradigms but can be synergistically combined. This challenges the prevailing dichotomy in optimizer design and suggests new directions for developing optimizers that exploit both geometric structure and adaptivity at appropriate granularities.
Practically, NorMuon’s distributed implementation under FSDP2 makes it suitable for LLM pretraining at scale, with minimal memory and computational overhead. The open-source release further facilitates adoption and benchmarking in the community.
Conclusion
NorMuon advances the state of the art in LLM optimization by integrating Muon’s orthogonalization with neuron-wise adaptive learning rates, yielding improved convergence, balanced parameter utilization, and scalable distributed training. The results indicate that combining geometric and adaptive preconditioning is a promising direction for future optimizer research, with potential applications beyond LLMs to other large-scale deep learning domains.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
NorMuon: Making Muon more efficient and scalable — explained simply
Overview
This paper is about a new way to train LLMs faster and more efficiently. Training these models uses an “optimizer,” which is like a rulebook that decides how to change the model’s numbers (its “weights”) to make it better. The popular optimizer Adam works well, but a newer one called Muon showed strong results by making updates go in balanced directions. The authors combine the best parts of both ideas into a new optimizer called NorMuon, which helps training go faster while using similar memory as Muon.
What questions did the researchers ask?
In simple terms, the paper asks:
- Can we mix Muon’s “balanced directions” with Adam’s “smart per-neuron sizing” to get even better training?
- Do some neurons (think of them as tiny workers in the network) get too much attention under Muon, making learning unbalanced?
- Can we fix that imbalance without using a lot more memory or slowing training too much?
- How can we make this work smoothly when training on many GPUs at once?
How did they do it? (Methods and ideas explained)
First, here are a few key ideas in everyday language:
- Optimizer: The method that decides how to change the model to improve it.
- Adam: Adjusts the learning rate (step size) for every single weight separately. This is stable but doesn’t consider how weights in the same layer relate.
- Muon: Changes the update directions so they don’t overlap too much (they become more “orthogonal”), which makes training more balanced across directions.
- Neuron-wise normalization: Instead of adjusting every weight, adjust at the level of each neuron (each row in a weight matrix), so no single neuron dominates.
- Momentum: A running average of past gradients (how much each weight should change), used to make smoother progress.
NorMuon combines these ideas in a simple cycle. At each training step, it:
- Builds momentum (a smooth average of recent gradients), like Muon.
- Orthogonalizes the momentum (makes update directions more balanced), like Muon.
- Measures how big the update is for each neuron (row) and normalizes it so all neurons get fair-sized updates (this is the new part).
- Scales the final step size so the overall change is similar to Adam’s typical size, keeping training stable.
- Updates the weights.
This approach keeps Muon’s good geometry (balanced directions), while making sure no neuron gets oversized updates. It uses very little extra memory because it only stores one number per neuron (instead of one per weight).
To make this work at large scale on many GPUs, they also designed a distributed version:
- They split the heavy “orthogonalize the momentum” job across devices so only one GPU computes it for a given matrix and then shares the result.
- Because the weights are split by rows (thanks to the FSDP2 framework), the per-neuron normalization can be done locally on each GPU without extra communication.
What did they find, and why is it important?
The main results show that NorMuon helps train big models faster and more efficiently:
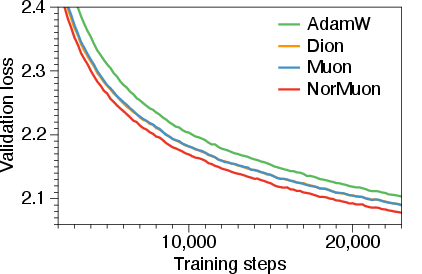
- On a 1.1 billion-parameter model, NorMuon needed about 21.74% fewer training steps than Adam to reach the same quality, and about 11.31% fewer than Muon.
- On a 5.4 billion-parameter model, NorMuon also beat both Adam and Muon with strong gains.
- NorMuon uses about the same memory as Muon (roughly half of Adam’s memory), since it only adds one small number per neuron.
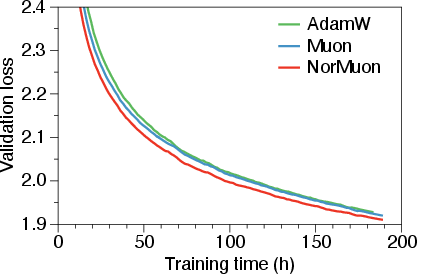
- The extra time per training step is small (around 3% more than Adam), but the faster progress means you still finish earlier overall.
- NorMuon works across different model sizes (from 124M up to 5.4B parameters), showing it’s broadly useful.
Why this matters: Training large models is expensive. Even small improvements in efficiency can save a lot of time and cost. NorMuon shows that mixing “balanced directions” (Muon) with “fair per-neuron sizes” (like Adam’s spirit, but lighter) is better than using either idea alone.
Simple discussion: What’s the impact?
- Complementary strengths: The paper shows that orthogonalizing updates (making directions balanced) and adapting per-neuron step sizes are not competing ideas — they work great together.
- Practical at scale: Their distributed implementation spreads the heavy work across GPUs, so it’s feasible for big training runs.
- Better use of the network: By keeping neuron updates similar in size, NorMuon prevents a few neurons from dominating, letting the whole model learn more evenly.
- Opens new optimizer designs: The success of NorMuon encourages future optimizers that mix geometric balancing with lightweight adaptive scaling.
In short, NorMuon helps LLMs learn faster, uses memory efficiently, and makes training fairer across all parts of the network — a win for both performance and practicality.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a focused list of unresolved issues that future work could address:
- Theoretical guarantees: no convergence analysis or regret bounds establishing when and why orthogonalization plus row-wise adaptivity yields faster optimization than Adam, Muon, or second-order methods; no formal link between improved singular-value conditioning, per-neuron norm equalization, and optimization rate/generalization.
- Bias correction: the method uses uncorrected EMAs for both first-order and second-order statistics; it remains unclear whether bias correction (as in Adam) improves stability or speed, especially in early training.
- Hyperparameter sensitivity: no ablations on key knobs such as β1/β2, ε, NS5 iteration count N, precision of NS5 (BF16 vs FP32), the fixed scaling constant 0.2 for RMS matching, weight decay magnitude and targeting, or learning-rate schedule interactions (e.g., Depth-μp).
- Post-orthogonalization normalization trade-off: after row-wise normalization, updates are no longer orthogonal. The extent to which this degrades the conditioning benefits of Muon is not theoretically or systematically quantified across layers/steps.
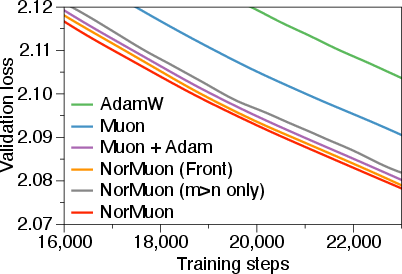
- When to normalize (m ≤ n vs m > n): although experiments suggest benefits even when m ≤ n, the paper lacks criteria for when normalization is helpful or harmful (e.g., as a function of rank, NS5 residual, or singular-value dispersion).
- Alternative normalization granularities: unexplored design space including column-wise normalization, per-head/group normalization, per-submodule normalization (e.g., Q/K/V separately), or mixed row/column/group schemes; no paper of their efficacy or cost.
- Coverage of baseline optimizers: no direct empirical comparison to Adam-mini (a closely related neuron/block-wise adaptive baseline) or to Shampoo/SOAP on smaller models where their memory is manageable; lack of comparison to Lion or other recent memory-efficient optimizers.
- Downstream and generalization performance: evaluation is restricted to pretraining validation loss; missing downstream benchmarks (zero-shot, few-shot, reasoning, coding), finetuning (SFT/RLHF), robustness (distribution shift, long-context), and calibration.
- Statistical robustness: results appear to be from single seeds; no reporting of variance, confidence intervals, or sensitivity to initialization/randomness.
- Scale limits: largest model is 5.4B and 50B tokens; open whether gains persist or change at 10B–70B+ scales and 100B–1T+ tokens, and under different tokenizer/data mixtures.
- Data and domain diversity: SlimPajama/FineWeb-only; no paper on other domains (code, multilingual, scientific), mixtures, or data-quality regimes (dedup levels, contamination).
- Long-sequence and batch-regime robustness: no ablations vs sequence length, microbatch size, gradient noise scale, or gradient clipping; open whether per-neuron normalization interacts with these regimes.
- QKV handling: the paper applies orthogonalization to concatenated QKV (and reports no Muon gain for separate Q/K/V), but does not evaluate separate vs concatenated for NorMuon; unclear if per-head/per-projection normalization or orthogonalization would help.
- Non-2D parameters and other layers: method targets 2D hidden-layer weights; unclear how to extend to convolutions, embeddings/unembedding (beyond defaulting to AdamW), layer norms, adapters/LoRA, rotary/positional params, or MoE experts/gating.
- Specialization vs equalization: equalizing per-neuron update norms may impede beneficial specialization or sparsity; no analysis of neuron activation/update distributions, dead neurons, or effects on pruning and structured sparsity.
- Weight decay and regularization interactions: weight decay is applied only to 2D parameters with a fixed value; no exploration of alternative decay targets, magnitudes, or interactions with orthogonalization/normalization and gradient clipping.
- NS5 design space and stability: no ablation on iteration count, damping, preconditioning, or alternative polar-decomposition approximations; numerical stability of NS5 in BF16 (over-/underflow, convergence failures) is unquantified.
- Singular spectrum tracking after normalization: while initial figures show low condition numbers, there’s no longitudinal analysis of singular-value spectra after normalization throughout training and across layers.
- Communication/computation scaling: distributed scheme is measured on one cluster/config; no scale-out paper vs GPU count, interconnect (NVLink vs Ethernet/IB), topology-aware scheduling, or overlap efficacy at higher concurrency.
- Temporary memory and kernels: reported memory focuses on persistent optimizer state; peak memory including NS5 workspaces and additional matmul buffers, and kernel-level performance (fusions, tiling), aren’t characterized.
- Device assignment strategy: the round-robin, size-sorted assignment for orthogonalization may be suboptimal under heterogeneous layers or nonuniform network topology; topology- and cost-aware scheduling remains open.
- Parallelism compatibility: interaction with tensor/pipeline/sequence parallelism, ZeRO variants, activation checkpointing, and overlap with attention/MLP kernels is not evaluated; potential deadlocks/stragglers and fault tolerance are unaddressed.
- Precision policies: effect of using FP8/BF16 for states and math (vs FP32), mixed-precision configurations for NS5, and their impact on stability, convergence, and memory are not explored.
- Criteria for adaptive application: no mechanism to detect when orthogonalization or row-wise normalization should be skipped or reduced (e.g., based on NS residual, rank deficiency, or gradient SNR) to save compute/comm without hurting quality.
- Training instability handling: no discussion of safeguards (gradient clipping, adaptive LR backoff, anomaly detection) for rare large updates after normalization; fixed RMS-matching factor (0.2) may not be universally safe.
- Reproducibility details: incomplete reporting of seeds, exact hardware/network specs, kernel/library versions, and detailed configs for distributed runs; important for verifying small overhead differences.
- Environmental and cost impact: efficiency gains are reported in steps and wall clock, but energy/CO2 or $ cost per loss target isn’t measured; open whether comm overhead negates energy savings at scale.
- Applicability to other objectives: behavior under instruction tuning, RLHF, multi-task training, contrastive or masked objectives, and continual/preference optimization remains unknown.
- Limitation on Dion comparison: Dion was omitted at 5.4B “due to resource constraints”; it remains unresolved whether NorMuon’s gains hold vs Dion at larger scales and with Dion’s amortized orthonormalization tuned.
Practical Applications
Immediate Applications
The following items are deployable now with the open-source NorMuon implementation and the described FSDP2-based distributed workflow.
- LLM pretraining cost and time reduction in industry (software, cloud, finance, e-commerce)
- Use case: Replace AdamW or Muon in Transformer pretraining to reach target validation loss with fewer steps (e.g., 21.74% fewer steps vs Adam on 1.1B, 13.91% on 5.4B), while keeping memory near Muon (~50% less than Adam).
- Tools/workflows: Drop-in PyTorch optimizer for hidden-layer 2D weights; keep Adam/AdamW for embeddings/bias; adopt NorMuon config with β1=0.95, β2=0.95; apply orthogonalization to concatenated QKV; use the FSDP2-based distributed implementation with momentum all-gather and update scatter in BF16.
- Assumptions/dependencies: PyTorch FSDP2 with row-wise sharding; GPUs with BF16 support; models with standard 2D weight matrices (Transformers); NS5 iterations configured; hyperparameters tuned (Depth-μp scaling, weight decay choices).
- Instruction tuning and domain fine-tuning at lower cost (healthcare, legal, education, enterprise IT)
- Use case: Reduce wall-clock and GPU-hours for supervised fine-tuning of base LLMs on domain-specific datasets; maintain stability with neuron-wise normalization and Muon-like conditioning.
- Tools/workflows: Integrate NorMuon into standard fine-tuning recipes; pair with PEFT methods (e.g., LoRA) while applying NorMuon to the unfrozen 2D mats; monitor per-neuron RMS norms to detect imbalances.
- Assumptions/dependencies: Benefits generalize from pretraining to fine-tuning; mixture of 2D and non-2D parameters handled (non-2D with AdamW); adequate batch sizes and sequence lengths.
- Academic experimentation and benchmarking (machine learning, optimization, systems)
- Use case: Study optimizer design trade-offs by toggling orthogonalization and normalization positions; reproduce ablations (e.g., Muon+Adam vs NorMuon) and extend to new architectures/datasets.
- Tools/workflows: Use the NorMuon open-source repo (https://github.com/zichongli5/NorMuon.git); integrate with public datasets (SlimPajama, FineWeb) and modded-NanoGPT baselines; log singular value spectra and per-neuron norm distributions.
- Assumptions/dependencies: Reproducibility relies on consistent data, depth scaling, and LR schedules; compute resources to run multi-scale experiments.
- MLOps/FinOps optimization (cloud cost control and scheduling)
- Use case: Cut training budget and carbon footprint by swapping optimizers or dynamically switching to NorMuon after warmup; implement “token-per-watt” dashboards.
- Tools/workflows: A/B test optimizers in CI/CD; collect time-to-accuracy metrics; automate optimizer selection by model depth and dataset; build cost calculators using measured 2.9–3.0% per-step time overhead vs AdamW and step reduction benefits.
- Assumptions/dependencies: Stable performance across varying token lengths and batch sizes; organization has monitoring infrastructure; cloud pricing and power usage effectiveness data available.
- Distributed training at scale (HPC, cloud AI platforms)
- Use case: Train multi-billion-parameter models more efficiently with NorMuon’s distributed orthogonalization distribution across devices to avoid replicated computation.
- Tools/workflows: Sort parameter tensors by size; round-robin assign orthogonalization work; overlap BF16 all-gather/scatter with NS5 compute; ensure row-wise sharded normalization is shard-local under FSDP2.
- Assumptions/dependencies: Correct FSDP2 configuration and shard mapping; interconnect bandwidth sufficient for added 33–50% communication volume; kernels optimized for NS5 in BF16.
- Startup and hobbyist model training (daily life, education)
- Use case: Train 124M–350M models (e.g., NanoGPT variants) faster on single or few GPUs; achieve 6–15% iteration reduction to reach target validation loss compared to Muon.
- Tools/workflows: Use default NorMuon settings in modded-NanoGPT; reduce electricity and time costs for local experimentation and educational projects.
- Assumptions/dependencies: Consumer GPUs support BF16 or fallback precision; modest datasets; limited distributed complexity.
- Sector-specific pretraining for internal copilots (software engineering, data analytics)
- Use case: Pretrain or continue-pretrain code and analytics models (e.g., SQL, Python) with improved optimizer conditioning, yielding better convergence within fixed training budgets.
- Tools/workflows: NorMuon optimizer module in internal LLM pipelines; orthogonality/per-neuron uniformity metrics as quality gates; combine with curriculum schedules and data deduplication.
- Assumptions/dependencies: Code/data distributions compatible with observed gains; 2D Transformer layers dominate training dynamics.
- Sustainability reporting enhancement (policy within organizations)
- Use case: Update “Green AI” reporting to include optimizer choice and training step reductions as energy-saving measures; mandate optimizer benchmarking before large training runs.
- Tools/workflows: Internal policies requiring NorMuon or equivalent when benefits exceed thresholds; dashboards attributing energy savings to optimizer changes; audits of optimizer configs.
- Assumptions/dependencies: Organizational buy-in; verifiable logs of training steps, energy, and emissions; consistent measurement methodology.
- Optimizer instrumentation and diagnostics (software tooling)
- Use case: Add runtime monitors for per-neuron RMS norms, singular value spectra of updates, and shard-local normalization stats to detect pathological training dynamics early.
- Tools/workflows: Lightweight PyTorch hooks around NorMuon to export telemetry; integrate with experiment trackers (Weights & Biases, MLflow) and alerting.
- Assumptions/dependencies: Minimal overhead on telemetry; meaningful thresholds for alerts; secure handling of metadata.
- Training recipes and playbooks for practitioners (education)
- Use case: Provide clear recipes for swapping in NorMuon in standard LLM training stacks and understanding when to retain AdamW for non-2D parameters.
- Tools/workflows: Public documentation with hyperparameters (β1=0.95, β2=0.95), LR schedules (Depth-μp), weight decay practices (0.1 on 2D hidden), and NS5 iteration guidance.
- Assumptions/dependencies: Practitioners follow recipes; versions of PyTorch/FSDP2 match tested environments.
Long-Term Applications
These items require further research, scaling, systems support, or productization before wide deployment.
- Hardware/kernel acceleration of orthogonalization (semiconductors, cloud AI)
- Use case: Fused CUDA/Triton kernels for NS5 iterations; accelerator-specific implementations (TPU, AWS Trainium, NVIDIA Blackwell) to reduce the ~3% step-time overhead further.
- Tools/products: “NorMuon Accelerated” kernels; vendor-supported libraries; compiler-level graph optimizations.
- Assumptions/dependencies: Vendor engagement; correctness under mixed precision; maintenance costs across architectures.
- Cross-domain extension to vision, speech, diffusion, and RL (healthcare imaging, multimedia, robotics)
- Use case: Apply neuron-wise normalized orthogonalized updates to ConvNets, ViTs, diffusion models, and policy networks to improve convergence and stability.
- Tools/workflows: Adapting row-wise statistics to non-Transformer architectures (e.g., channel-wise for CNNs); exploring orthogonalization for convolutional kernels.
- Assumptions/dependencies: Empirical validation beyond LLMs; redefinition of “neuron” for layer types; task-specific hyperparameter tuning.
- AutoML/auto-optimizer orchestration (software platforms)
- Use case: Systems that choose between AdamW, Muon, NorMuon, Dion, Shampoo/SOAP based on live telemetry (conditioning, per-neuron variance, memory budget).
- Tools/products: “Optimizer Orchestrator” service that hot-swaps optimizers mid-training; policy rules informed by model depth, token length, loss curvature.
- Assumptions/dependencies: Reliable online metrics; safe optimizer switching; framework support for seamless state transfers.
- 8-bit/quantized optimizer states and memory compression (systems, edge AI)
- Use case: Combine NorMuon with optimizer state quantization to push memory savings beyond Muon while preserving conditioning and neuron-wise normalization benefits.
- Tools/workflows: 8-bit momentum buffers; error-compensation schemes; mixed-precision NS5.
- Assumptions/dependencies: Accuracy retention under quantization; stable training with compressed states; hardware support.
- Federated and on-device training with balanced updates (mobile, IoT)
- Use case: Use NorMuon’s per-neuron normalization to prevent client drift and dominate neurons in federated settings, improving robustness and fairness across devices.
- Tools/workflows: Federated optimizers with orthogonalization computed locally or server-side; communication-efficient variants (e.g., low-rank orthonormalization à la Dion).
- Assumptions/dependencies: Privacy constraints; limited bandwidth; adaptation of the distributed algorithm to FL aggregation.
- Standards for energy-efficient AI training (policy, sustainability)
- Use case: Formalize “energy-per-token” and “steps-to-target” benchmarks that include optimizer selection; certification for training runs achieving threshold efficiencies.
- Tools/products: Industry standards bodies (e.g., MLPerf-like tracks) incorporating optimizer metrics; reporting templates used in ESG disclosures.
- Assumptions/dependencies: Consensus on metrics; third-party audits; alignment with regulatory frameworks.
- Deeper theory and safety guarantees (academia, safety-critical sectors)
- Use case: Analytical bounds on conditioning and per-neuron variance; robustness claims (e.g., avoiding neuron dominance) for safety-critical applications (medical, aviation NLP).
- Tools/workflows: Theoretical analysis of approximate orthogonalization and normalization; test suites for pathological cases.
- Assumptions/dependencies: Mathematical tractability; task-specific safety criteria; datasets representative of risk scenarios.
- Integration into major training frameworks (ecosystem)
- Use case: First-class NorMuon support in DeepSpeed, Megatron-LM, JAX/Flax, and Hugging Face Accelerate; turnkey distributed recipes.
- Tools/products: Official plugins; config templates; cluster-aware parameter assignment and communication overlap strategies.
- Assumptions/dependencies: Maintainers’ bandwidth; compatibility with each framework’s sharding model; reproducibility across stacks.
- NorMuon-based managed cloud SKUs (cloud providers)
- Use case: “Optimized Training” instance types that standardize NorMuon kernels, telemetry, and FinOps calculators to guarantee cost/performance gains for LLM training.
- Tools/products: Managed services exposing NorMuon; SLAs tied to time-to-accuracy improvements; dashboards for optimizer impact.
- Assumptions/dependencies: Provider willingness; customer demand; consistent performance across workloads.
- Hybrid second-order/orthogonalization methods (optimization research)
- Use case: Explore combining low-cost curvature estimates (e.g., Kronecker-factored approximations) with orthogonalization and neuron-wise scaling for further gains without large memory hits.
- Tools/workflows: SOAP/Shampoo-inspired variants with NorMuon normalization; adaptive selectivity by layer type and size.
- Assumptions/dependencies: Careful memory/communication budgeting; numerical stability; mature distributed implementations.
Notes on Assumptions and Dependencies (cross-cutting)
- NorMuon’s strongest evidence is for LLM pretraining with Transformer architectures where 2D hidden-layer matrices dominate; effects may vary in other domains and layer types.
- The distributed benefits assume FSDP2 row-wise sharding and careful work assignment; different sharding schemes may require adaptation.
- Communication overhead increases (≈33% with FP32 parameters; ≈50% with BF16) must be mitigated by compute overlap and sufficient interconnect bandwidth.
- Gains rely on appropriate hyperparameters (β1≈0.95, β2≈0.95, NS5 iterations, LR schedules with Depth-μp) and weight-decay practices (e.g., 0.1 on 2D hidden layers).
- Orthogonalization accuracy depends on NS5 approximations; future kernel improvements and precision choices can affect stability and performance.
Glossary
- AdaFactor: An adaptive optimizer that reduces memory by factorizing second-moment statistics across rows and columns. "This memory cost motivated techniques like AdaFactor \citep{adafactor}, which factorizes the second-moment accumulator across rows and columns to reduce memory."
- AdaGrad: An optimizer that adapts learning rates per-parameter based on accumulated squared gradients. "Optimizers such as AdaGrad \citep{Adagrad}, RMSProp \citep{hinton2012rmsprop}, Adam \citep{adam} and AdamW \citep{adamw} use first- and second-moment estimates"
- Adam-mini: An optimizer that assigns one adaptive rate per block (e.g., neuron) leveraging near-block-diagonal Hessian structure to cut memory. "Adam-mini \citep{adammini} exploits the near-block-diagonal Hessian structure of neural networks"
- AdamW: Adam with decoupled weight decay for better regularization behavior. "AdamW \citep{adamw}, the standard adaptive optimizer with decoupled weight decay"
- All-gather: A distributed communication primitive that gathers tensors from all devices to all devices. "4 bytes (forward all-gather) + 4 bytes (backward all-gather) + 4 bytes (gradient reduce-scatter) = 12 bytes."
- Amortized power iteration: A low-rank iterative method run intermittently to approximate leading subspaces for orthonormalization. "Dion applies a low-rank orthonormalization scheme via amortized power iteration instead of full Newton–Schulz"
- BF16: Brain floating point 16-bit format used to reduce memory/communication while keeping dynamic range. "With NS5 iteration computed in BF16 precision, NorMuon requires:"
- Block-wise adaptive learning rates: Scaling updates using one adaptive statistic per parameter block (e.g., per neuron) rather than per-coordinate. "combine Muon's orthogonalization with block-wise adaptive learning rates"
- Condition number: The ratio of largest to smallest singular value; measures how ill-conditioned an update or matrix is. "Singular value distribution reveals that raw momentum and AdamW's update exhibit high condition numbers."
- Coordinate-wise preconditioning: Per-parameter rescaling of updates using local statistics (e.g., second moments). "achieves robust performance through coordinate-wise preconditioning:"
- Curvature information: Second-order structure of the loss surface (e.g., Hessian) that guides informed preconditioning. "employ full-matrix preconditioning through singular value decomposition to capture curvature information and parameter interdependencies."
- Decoupled weight decay: Regularization applied directly to weights, separate from the gradient-based update. "the standard adaptive optimizer with decoupled weight decay"
- Depth-μp: A scaling rule that adjusts learning rates with network depth for stable training. "We employ Depth-p \citep{depthmup} to scale the learning rate inversely proportional to based on model depth."
- Dion: A distributed optimizer that applies low-rank orthonormalized updates for efficient scaling. "More recently, Dion \citep{dion} extends the orthogonal update paradigm to be more communication- and compute-efficient in distributed settings."
- Exponential moving average (EMA): A decayed running average used to smooth first- or second-order statistics. "when considered without exponential moving averages (EMAs),"
- FSDP2: PyTorch’s Fully Sharded Data Parallel v2 framework that shards parameters, grads, and optimizer states across devices. "We develop a distributed version of NorMuon compatible with the FSDP2 framework \citep{pytorch-fsdp2}."
- Frobenius norm: The square root of the sum of squared matrix entries; a matrix analog of the L2 norm. "Starting with the Frobenius-normalized momentum "
- GaLore: A memory-efficient method that maintains momentum in a low-rank gradient subspace. "GaLore \citep{galore} maintains momentum in a low-rank subspace derived from the SVD of gradients"
- Hessian: The matrix of second derivatives of the loss, encoding local curvature. "Adam-mini \citep{adammini} exploits the near-block-diagonal Hessian structure of neural networks"
- K-FAC: Kronecker-Factored Approximate Curvature; a second-order optimizer using structured curvature approximations. "K-FAC \citep{kfac} and its variants \citep{martens2018kronecker, gao2021trace} approximate curvature information beyond individual coordinates"
- Kronecker-factored preconditioners: Preconditioners built from Kronecker product factorizations of curvature approximations. "Shampoo \citep{shampoo} and its distributed variant \citep{distributedshampoo} employ Kronecker-factored preconditioners"
- L2 normalization: Scaling a vector or matrix so its L2 norm (or per-block L2) matches a target value. "apply normalization at the per-coordinate and per-neuron levels respectively"
- Lion: An optimizer using sign-based updates to save memory by avoiding second-moment buffers. "Lion \citep{lion} applies a coordinate-wise signed update, abandoning second-order moment estimates to achieve memory savings."
- Megatron-LM: A framework for large-scale LLM training with model/data parallelism. "ZeRO-1 with Megatron-LM \citep{zero123, shoeybi2019megatron}"
- Muon: An optimizer that orthogonalizes momentum updates via approximate polar decomposition to improve conditioning. "Muon performs an approximate polar decomposition (via Newton–Schulz iterations) on the momentum to extract its orthogonal component"
- Newton–Schulz iterations: An iterative method to approximate matrix functions (e.g., polar factors) efficiently. "Muon approximates this orthogonalization through a fixed number of Newton-Schulz iterations."
- NorMuon: An optimizer combining Muon’s orthogonalization with neuron-wise adaptive scaling for balanced updates. "NorMuon (Neuron-wise Normalized Muon), an optimizer that synergistically combines orthogonalization with neuron-level adaptive learning rates."
- NS5: A fixed-step Newton–Schulz-based operator used to orthogonalize update matrices. "The critical component is the orthogonalization operator "
- Orthogonal polar factor: The orthogonal component in a matrix’s polar decomposition. "applying truncated Newton-Schulz iterations to approximate the orthogonal polar factor of momentum matrices."
- Orthogonal projection: Projection of a matrix onto the set of orthogonal matrices (closest in Frobenius norm). "which aims to approximate the orthogonal projection of the momentum matrix:"
- Orthogonalization: Transforming updates so their singular values are balanced (ideally all ones), improving conditioning. "Muon's orthogonalization effectively eliminates this imbalance."
- Orthonormalization: Producing vectors (or updates) that are both orthogonal and unit-norm. "Dion applies a low-rank orthonormalization scheme via amortized power iteration"
- Polar decomposition: Factorization of a matrix into an orthogonal part and a symmetric positive-semidefinite part. "performs an approximate polar decomposition (via Newton–Schulz iterations)"
- Preconditioning granularity: The scale at which an optimizer rescales updates (coordinate, block, or matrix level). "These optimizers fundamentally differ in their preconditioning granularity and objectives."
- QKV matrix: The concatenated query-key-value projection matrix used in Transformer attention. "we apply orthogonalization to the concatenated QKV matrix rather than separately"
- Reduce-scatter: A distributed primitive that reduces tensors across devices and scatters the result shards. "4 bytes (forward all-gather) + 4 bytes (backward all-gather) + 4 bytes (gradient reduce-scatter) = 12 bytes."
- RMS norm: Root-mean-square norm used for scaling updates to match a desired magnitude. "we add a learning rate scaling following \citep{muon} to keep a similar RMS norm to match Adam's RMS norm (line 10)."
- Row-wise normalization: Normalizing each row (e.g., per-neuron) to balance update magnitudes. "applying row-wise normalization after orthogonalization"
- Row-wise sharding: Partitioning parameters by rows across devices to localize per-row operations. "we leverage FSDP2's row-wise parameter sharding to enable efficient neuron-wise normalization"
- Second-order momentum: The EMA of squared updates/gradients used to adapt learning rates. "maintaining second-order momentum statistics for each neuron"
- Shampoo: A second-order optimizer using Kronecker-factored preconditioners for tensor parameters. "Shampoo \citep{shampoo} and its distributed variant \citep{distributedshampoo} employ Kronecker-factored preconditioners"
- SOAP: A method improving/stabilizing Shampoo, bridging it with Adafactor. "SOAP \citep{soap} establishes a connection between Shampoo and Adafactor and further improves convergence performance."
- SVD (Singular Value Decomposition): Factorization expressing a matrix via singular values and orthogonal factors. "derived from the SVD of gradients"
- ZeRO-1: A sharding strategy that partitions optimizer states to reduce memory without fully sharding parameters. "ZeRO-1 with Megatron-LM \citep{zero123, shoeybi2019megatron}"
- ZeRO-3: A full sharding approach that partitions parameters, gradients, and optimizer states across devices. "which employs ZeRO-3 style \citep{zero123} sharding to partition optimizer states, parameters, and gradients across multiple devices."
Collections
Sign up for free to add this paper to one or more collections.
