Walking, Rolling, and Beyond: First-Principles and RL Locomotion on a TARS-Inspired Robot (2510.05001v1)

Abstract: Robotic locomotion research typically draws from biologically inspired leg designs, yet many human-engineered settings can benefit from non-anthropomorphic forms. TARS3D translates the block-shaped 'TARS' robot from Interstellar into a 0.25 m, 0.99 kg research platform with seven actuated degrees of freedom. The film shows two primary gaits: a bipedal-like walk and a high-speed rolling mode. For TARS3D, we build reduced-order models for each, derive closed-form limit-cycle conditions, and validate the predictions on hardware. Experiments confirm that the robot respects its +/-150 degree hip limits, alternates left-right contacts without interference, and maintains an eight-step hybrid limit cycle in rolling mode. Because each telescopic leg provides four contact corners, the rolling gait is modeled as an eight-spoke double rimless wheel. The robot's telescopic leg redundancy implies a far richer gait repertoire than the two limit cycles treated analytically. So, we used deep reinforcement learning (DRL) in simulation to search the unexplored space. We observed that the learned policy can recover the analytic gaits under the right priors and discover novel behaviors as well. Our findings show that TARS3D's fiction-inspired bio-transcending morphology can realize multiple previously unexplored locomotion modes and that further learning-driven search is likely to reveal more. This combination of analytic synthesis and reinforcement learning opens a promising pathway for multimodal robotics.

• The paper introduces a framework that combines analytic modeling with deep reinforcement learning to develop multimodal locomotion on TARS3D.
• It offers detailed analytical models for bipedal and rolling gaits, including closed-form limit-cycle conditions verified through hardware experiments.
• The study highlights the crucial role of structural and reward-based priors in guiding the learning process towards energy-efficient and robust locomotion.

Analytical and Learning-Based Locomotion on TARS3D: A Technical Review

Introduction

This paper presents a comprehensive paper of locomotion strategies on TARS3D, a robot inspired by the fictional TARS from Interstellar. The work integrates first-principles analytical modeling with deep reinforcement learning (DRL) to realize and expand the repertoire of gaits on a non-anthropomorphic, kinematically redundant platform. The research demonstrates that fiction-inspired morphologies, when combined with both analytic and learning-based approaches, can yield robust, multimodal locomotion beyond conventional biomimetic paradigms.

Figure 1: Primary locomotion modes emulated by TARS: (left) bipedal-like gait, (right) rolling gait.

Mechanical Design and System Architecture

TARS3D is a 0.25 m, 0.99 kg robot with four telescopic legs, each actuated by a Robotis Dynamixel 2XL430-W250, providing both rotary hip and prismatic extension. The design supports eight degrees of freedom, with three active hips and one passive/free-spinning joint. The legs terminate in curved foot plates (radius 0.124 m, 45° arc), enabling both walking and rolling gaits. The actuation and sensing stack is built for high power density and precise position control, with a 100 Hz PID loop and 12-bit encoders.

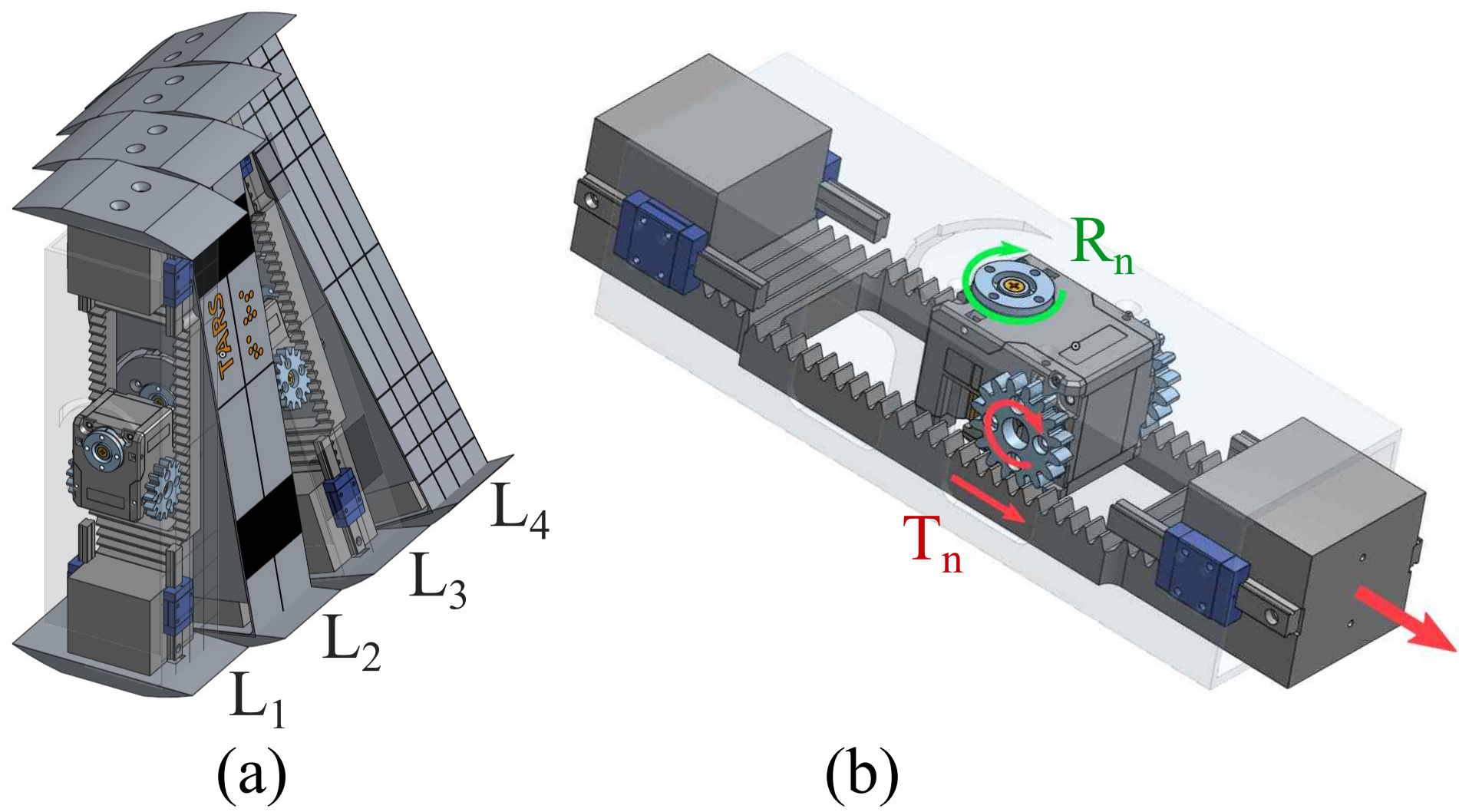
Figure 2: TARS3D mechanical design: (a) overall CAD model of the 4-leg ($L_1, ..., L_4$) assembly.

Analytical Modeling of Locomotion Modes

Bipedal Gait

The bipedal gait is modeled as a passive curved-foot walker, following canonical rimless-wheel and compass-gait frameworks. The gait cycle consists of alternating stance and swing phases for inner and outer legs, with energy balance governed by gravitational work and collision losses. The analytical model yields closed-form limit-cycle conditions, targeting a 35 mm stride at 0.18 m/s. Hardware validation confirms stable walking, with the robot respecting its ±150° hip limits and alternating contacts without interference.

Figure 3: Phases of bipedal gait of TARS3D.

Figure 4: Four phases of TARS3D bipedal gait.

Rolling Gait

The rolling gait leverages the robot's ability to reconfigure into a double rimless-wheel morphology, with each leg acting as four spokes. The analytical model derives the dynamics of the rolling cycle, including angular momentum conservation, collision maps, and the required center-of-gravity (CoG) shift via telescopic leg extension. The model predicts an eight-step hybrid limit cycle, with each body roll completed in eight ground contacts. The rolling gait achieves $v \approx 0.51$ m/s and cost of transport (CoT) $\approx 0.145$, comparable to state-of-the-art rimless-wheel runners, despite limited joint rotation.

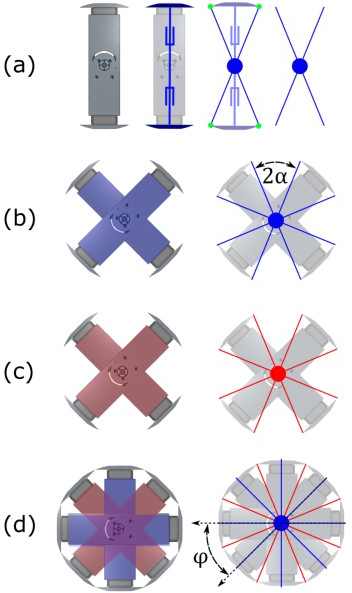
Figure 5: Double rimless-wheel morphology of TARS3D.

Figure 6: Phases of rolling gait in double rimless-wheel model.

Deep Reinforcement Learning for Gait Discovery

Training Setup

DRL is employed to explore the high-dimensional gait space afforded by TARS3D's kinematic redundancy. The robot is simulated in NVIDIA IsaacLab, with a reward function combining forward velocity, uprightness, energy efficiency, and joint limit adherence. PPO is used for policy optimization, with a 3-layer MLP and GPU-parallelized training across 2048 environments, achieving convergence in under 15 minutes on consumer hardware.

Emergent Behaviors

DRL successfully recovers the analytic bipedal and rolling gaits when seeded with appropriate priors (e.g., joint angle constraints for rolling). Without such priors, the agent discovers novel behaviors, including asymmetric pacing and frog-like hopping, but fails to converge to the rolling gait. This underscores the necessity of embedding structural priors and reward shaping for complex, high-symmetry motions.

Figure 7: Behaviors learned through Deep RL.

Terrain Adaptation

The robustness of learned policies is evaluated on randomized terrain. Direct training on uneven surfaces favors walking over rolling, while transferring a flat-ground rolling policy maintains stability up to $\pm 0.16 l_0$ terrain uncertainty. Beyond this, rolling degrades, with a marked drop in success rate and increased heading drift due to perturbed leg placement.

Figure 8: TARS3D rolling on randomized terrain with $\pm 0.16 l_0$ uncertainty.

Comparison of Analytical and Learned Gaits

Quantitative analysis of the CoM trajectories reveals close correspondence between the RL-learned rolling gait and the analytical model, validating the theoretical framework and the efficacy of model-based priors in guiding learning.

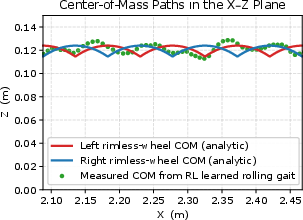
Figure 9: CoM of TARS3D's rolling gait from analytical model vs. RL-learned gait.

Discussion

Multimodal Locomotion from Non-Anthropomorphic Morphology

The paper demonstrates that a simple, fiction-inspired morphology can support multiple, fundamentally distinct gaits. Analytical models provide interpretable seed solutions, while DRL explores the broader gait manifold, uncovering behaviors not captured by first-principles analysis. The rolling gait, in particular, achieves high speed and efficiency with limited-range joints, a result not attainable in traditional rimless-wheel robots.

Role of Priors in Learning

The necessity of structural and reward-based priors for learning complex gaits is highlighted. While DRL excels at discovering novel low-speed behaviors, high-symmetry, energy-efficient modes like rolling require explicit guidance. This suggests a generalizable workflow: analytic synthesis followed by data-driven exploration, with priors bridging the gap between theory and practice.

Limitations and Future Directions

Current limitations include tethered operation, restricted terrain diversity, and limited sim-to-real transfer for learned gaits. Future work should address untethered autonomy, robust mode switching, adaptation to compliant and unstructured surfaces, and integration of richer sensory feedback. Quantitative energetic analysis and broader terrain testing will further elucidate the operational envelope of TARS3D.

Conclusion

This paper establishes a rigorous framework for multimodal locomotion on non-anthropomorphic robots, integrating analytic modeling and reinforcement learning. TARS3D validates cinematic gaits and uncovers novel behaviors, demonstrating that fiction-inspired morphology, when coupled with principled control and learning, can expand the design space of mobile robotics. The results have implications for the development of versatile, task-specific robots in engineered environments, and suggest future research directions in hybrid analytic-learning workflows and morphology-driven gait synthesis.