Score-based Greedy Search for Structure Identification of Partially Observed Linear Causal Models (2510.04378v1)

Abstract: Identifying the structure of a partially observed causal system is essential to various scientific fields. Recent advances have focused on constraint-based causal discovery to solve this problem, and yet in practice these methods often face challenges related to multiple testing and error propagation. These issues could be mitigated by a score-based method and thus it has raised great attention whether there exists a score-based greedy search method that can handle the partially observed scenario. In this work, we propose the first score-based greedy search method for the identification of structure involving latent variables with identifiability guarantees. Specifically, we propose Generalized N Factor Model and establish the global consistency: the true structure including latent variables can be identified up to the Markov equivalence class by using score. We then design Latent variable Greedy Equivalence Search (LGES), a greedy search algorithm for this class of model with well-defined operators, which search very efficiently over the graph space to find the optimal structure. Our experiments on both synthetic and real-life data validate the effectiveness of our method (code will be publicly available).

• The paper introduces LGES, the first score-based greedy search algorithm with formal identifiability guarantees for partially observed linear causal models under GNFM.
• It demonstrates that maximizing the likelihood score while minimizing model dimension recovers the true causal structure under generalized faithfulness, bridging algebraic and Markov equivalence.
• Empirical results reveal that LGES outperforms existing methods on both synthetic and real-world datasets, showing high F1 scores, lower SHD, and improved fit indices.

Score-Based Greedy Search for Structure Identification of Partially Observed Linear Causal Models

Introduction and Motivation

The paper addresses the problem of causal structure identification in linear SEMs with latent variables, a scenario prevalent in scientific domains where causal sufficiency is violated. Traditional constraint-based methods (e.g., FCI, rank/tetrad constraints, high-order moments) suffer from error propagation and multiple testing, especially in high-dimensional, small-sample regimes. Score-based methods, such as GES, offer practical advantages but have not been extended with identifiability guarantees to the partially observed setting. This work introduces the first score-based greedy search algorithm—Latent variable Greedy Equivalence Search (LGES)—for structure identification in partially observed linear causal models, with formal identifiability guarantees under the Generalized N Factor Model (GNFM) graphical assumption.

Theoretical Foundations: Algebraic and Markov Equivalence

The core theoretical contribution is the characterization of identifiability via likelihood score and model dimension. The authors show that, under generalized faithfulness, maximizing the likelihood score and minimizing model dimension yields a structure algebraically equivalent to the ground truth. However, without further graphical assumptions, the algebraic equivalence class is uninformatively large (Figure 1).

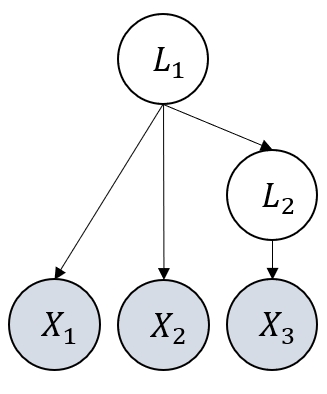
Figure 1: Without further graphical assumption, the algebraic equivalence class is very large and not very informative: suppose the ground truth $G^*$ in (a), by Theorem 1 we may arrive at either $\hat{G}_1$ (b) or $\hat{G}_2$ (c), both algebraically equivalent to $G^*$.

To address this, the Generalized N Factor Model (GNFM) is introduced, which generalizes the one-factor model by allowing latent variables to be partitioned into groups with shared observed children and flexible inter-group relations. Under GNFM, algebraic equivalence implies Markov equivalence, enabling unique recovery of the underlying structure up to the Markov Equivalence Class (MEC) via score-based search.

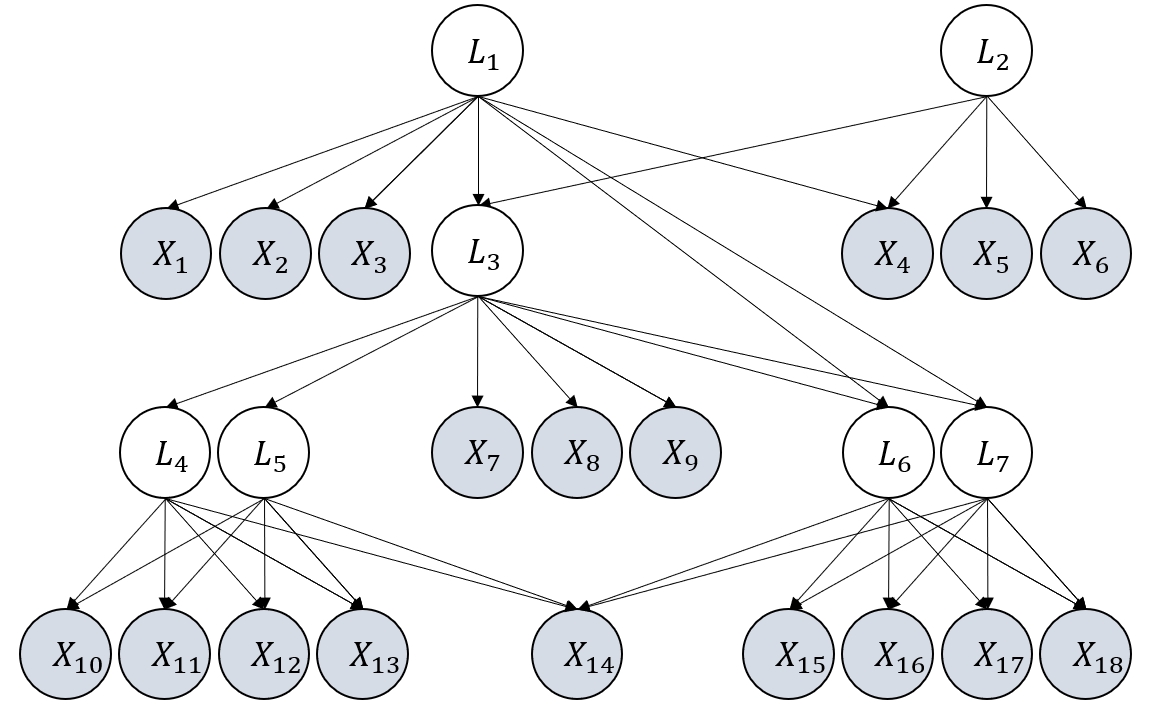
Figure 2: Illustrative examples to compare two graphical assumptions, generalized N factor model v.s. one factor model.

LGES Algorithm: Score-Based Greedy Search

LGES is a two-phase greedy search algorithm operating over the space of CPDAGs:

• Phase 1: Identifies the structure between latent and observed variables by iteratively deleting edges from latent to observed nodes, retaining deletions only if the likelihood score remains optimal within a tolerance $\delta$. This phase leverages rank constraints to identify pure children of latent groups.
• Phase 2: Identifies the structure among latent variables by deleting edges between latent groups, again guided by the likelihood score. The process is guaranteed to converge to the correct MEC under GNFM and generalized faithfulness.

The algorithm avoids explicit computation of model dimension and is computationally efficient, with parallelizable steps and polynomial complexity under sparsity assumptions.

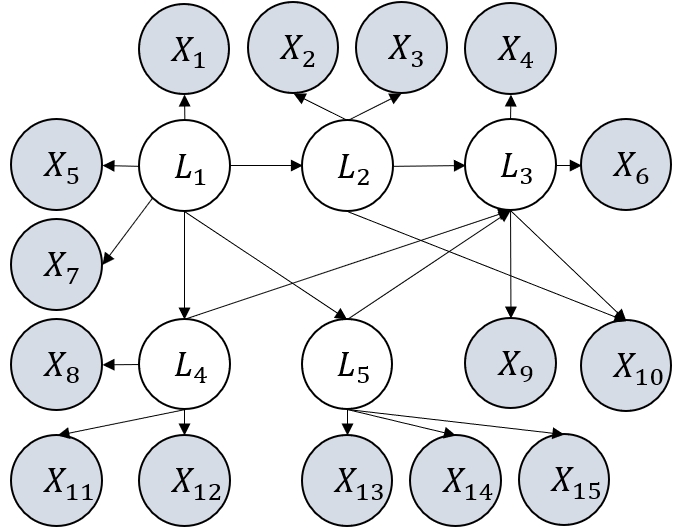
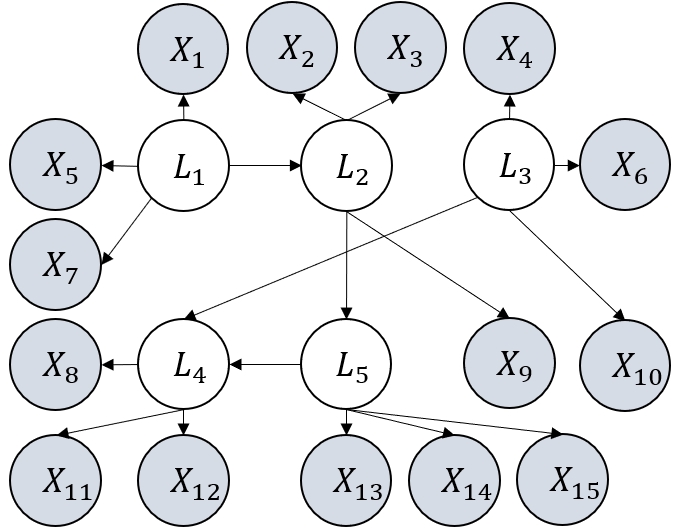
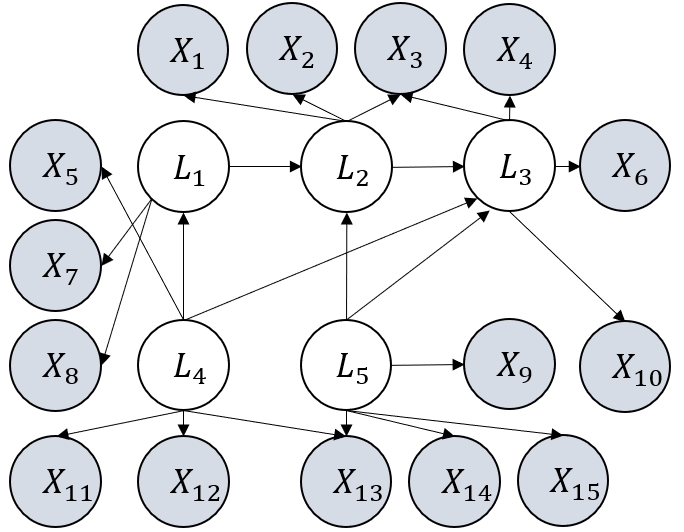
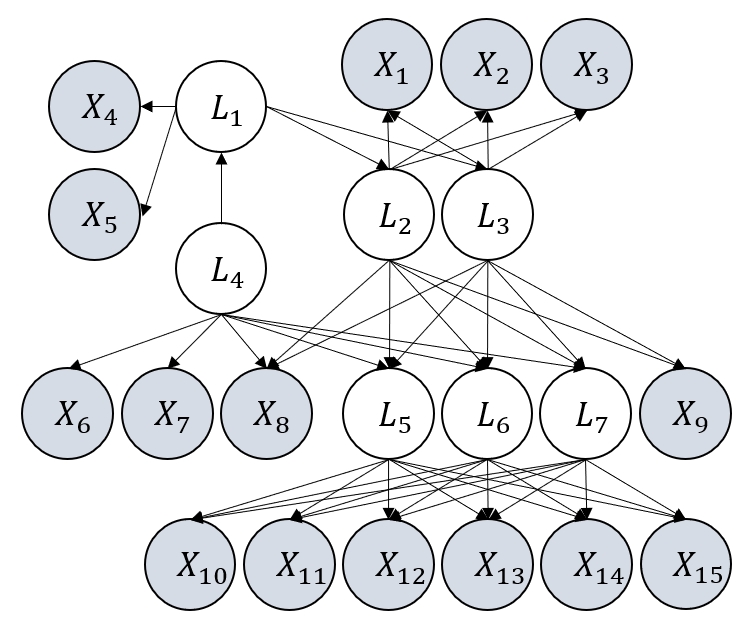
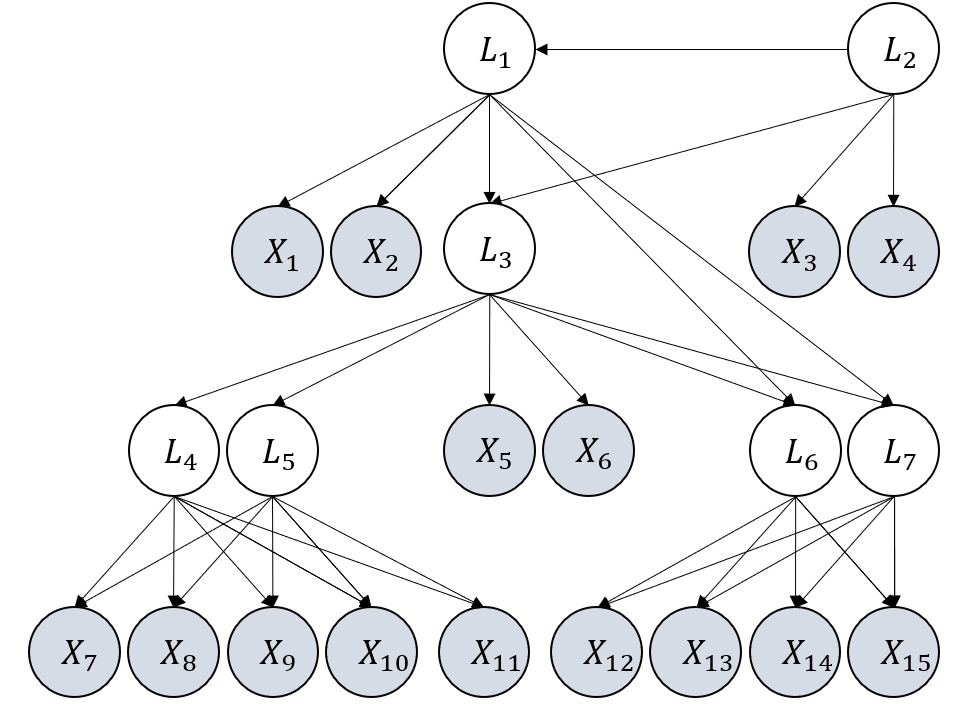
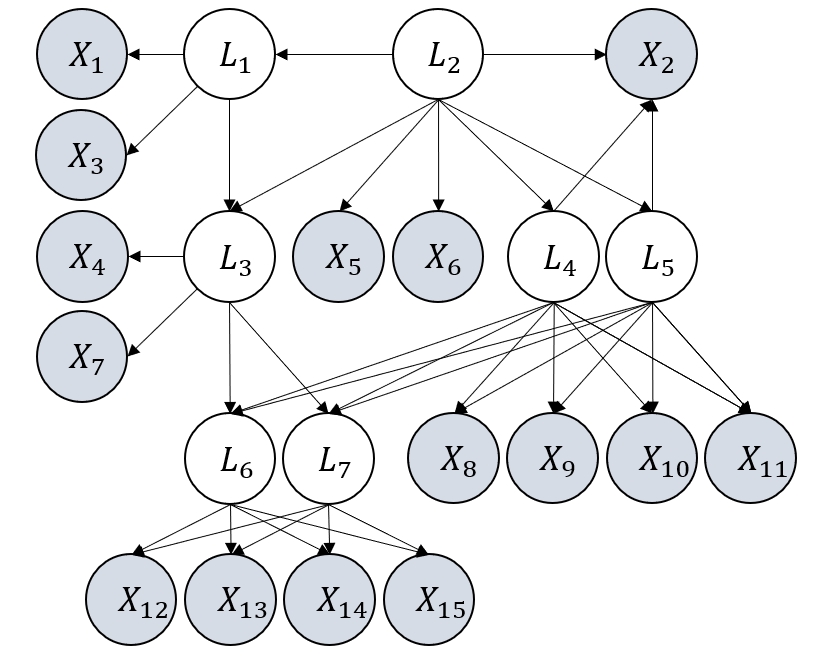
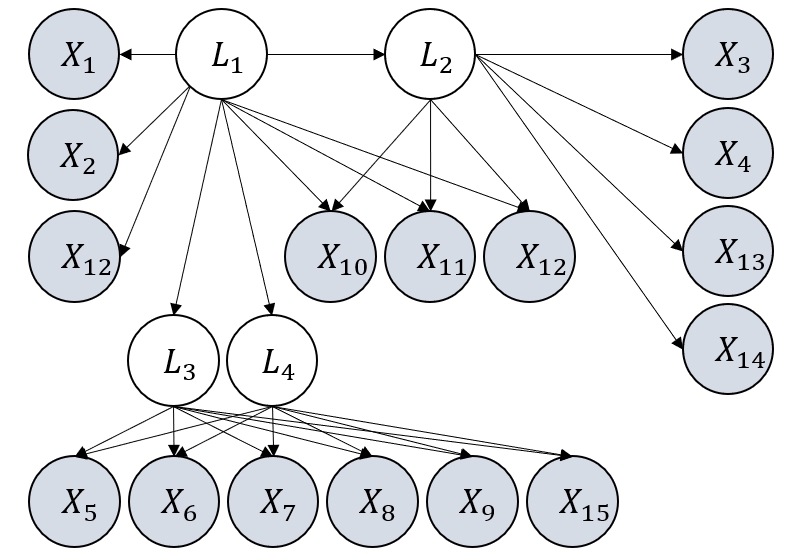
Figure 3: Examples of graphs considered in our experiments. They satisfy the definition of GNFM.

Empirical Evaluation

Synthetic Data

LGES is benchmarked against FOFC, GIN, and RLCD on synthetic graphs satisfying GNFM. Metrics include F1 score (skeleton) and SHD (MEC). LGES consistently outperforms baselines, especially in small-sample regimes, demonstrating robustness to error propagation and multiple testing. For instance, with $N=1000$, LGES achieves F1=0.82 and SHD=8.8, outperforming RLCD (F1=0.76, SHD=11.24).

Model Misspecification

LGES maintains strong performance under non-Gaussian noise and moderate nonlinearity (leaky ReLU), with only marginal degradation in F1 and SHD. This is attributed to the identifiability theory relying on constraints imposed by structure on the covariance matrix, which are invariant to noise distribution and certain nonlinearities.

Real-World Data

LGES is applied to the Big Five personality, teacher burnout, and multitasking datasets. The recovered structures align with domain knowledge and outperform established models in RMSEA, CFI, and TLI fit indices, indicating superior explanatory power.

Implementation and Scalability

The algorithm is implemented in Python/PyTorch, with optimization via Adam and LBFGS. The tolerance parameter $\delta$ is set as $0.25 \log(N)/N$, analogous to BIC regularization in GES. LGES is insensitive to small changes in $\delta$ and scales efficiently to graphs with 20+ variables, with runtimes on the order of one minute per instance.

Limitations and Extensions

The identifiability guarantees are established for linear models under GNFM and generalized faithfulness. While empirical results indicate robustness to non-Gaussianity and moderate nonlinearity, theoretical extensions to fully nonlinear models remain open. The method is not designed for cyclic or nonparametric SEMs, and identifiability in those regimes requires further investigation.

Implications and Future Directions

Practically, LGES enables reliable causal structure discovery in partially observed systems, with applications in psychology, genomics, and social sciences. Theoretically, the work bridges algebraic and Markov equivalence in latent variable models and demonstrates the feasibility of scalable score-based search with identifiability guarantees. Future research may extend the framework to nonlinear SEMs, cyclic graphs, and integrate interventional data for enhanced identifiability.

Conclusion

This paper establishes a rigorous foundation for score-based greedy search in partially observed linear causal models, introducing the GNFM assumption and the LGES algorithm. The approach achieves asymptotic consistency, practical scalability, and superior empirical performance, advancing the state-of-the-art in latent variable causal discovery.