Understanding the Role of Training Data in Test-Time Scaling (2510.03605v1)

Abstract: Test-time scaling improves the reasoning capabilities of LLMs by allocating extra compute to generate longer Chains-of-Thoughts (CoTs). This enables models to tackle more complex problem by breaking them down into additional steps, backtracking, and correcting mistakes. Despite its strong performance--demonstrated by OpenAI's o1 and DeepSeek R1, the conditions in the training data under which long CoTs emerge, and when such long CoTs improve the performance, remain unclear. In this paper, we study the performance of test-time scaling for transformers trained on an in-context weight prediction task for linear regression. Our analysis provides a theoretical explanation for several intriguing observations: First, at any fixed test error, increasing test-time compute allows us to reduce the number of in-context examples (context length) in training prompts. Second, if the skills required to solve a downstream task are not sufficiently present in the training data, increasing test-time compute can harm performance. Finally, we characterize task hardness via the smallest eigenvalue of its feature covariance matrix and show that training on a diverse, relevant, and hard set of tasks results in best performance for test-time scaling. We confirm our findings with experiments on large, nonlinear transformer architectures.

• The paper demonstrates that increasing test-time chain-of-thought steps acts like a pseudo-Newton update for weight estimation in transformer models.
• It establishes that task hardness, quantified via the feature covariance spectrum, controls the trade-off between training data coverage and additional compute at inference.
• Empirical validation on LSA and GPT-2 models confirms that diverse, hard training examples optimize performance and inform resource scaling laws.

Theoretical and Empirical Analysis of Training Data in Test-Time Scaling

Overview

This paper provides a rigorous theoretical and empirical investigation into the mechanisms by which training data properties affect the efficacy of test-time scaling in transformer-based models, particularly in the context of in-context learning (ICL) for linear regression. The work formalizes the relationship between training data diversity, task hardness, and the benefits and pitfalls of allocating additional compute at inference via longer chain-of-thought (CoT) reasoning. The analysis is grounded in explicit characterizations of transformer dynamics, with extensions to multi-task settings and validation on both linear and nonlinear (GPT-2) architectures.

Formalization of In-Context Learning and Test-Time CoT

The authors consider a transformer trained on an in-context weight prediction task for linear regression, where each prompt is associated with a different weight vector and feature distribution. The model is trained to directly estimate the weight vector from a prompt, using a linear self-attention (LSA) architecture. The key insight is that, although CoT is not used during training, at test time the model can be prompted to generate multiple intermediate reasoning steps, effectively implementing a multi-step (pseudo-)Newton’s method for loss minimization.

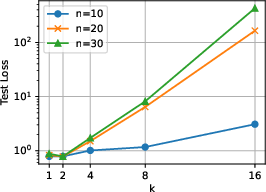
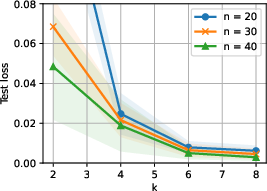
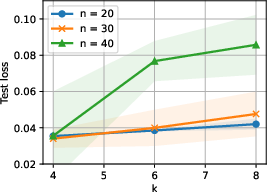
Figure 1: Schematic of the LSA architecture used for in-context weight prediction, highlighting the embedding structure and self-attention mechanism.

The theoretical analysis demonstrates that, under suitable initialization and training, gradient descent converges to a global minimum, and the resulting transformer parameters can be explicitly characterized. At test time, the recursive update of the weight estimate $w_{i+1}$ is shown to correspond to a Newton-like update, with the number of CoT steps $k$ controlling the depth of reasoning.

Task Hardness and Scaling Laws

A central contribution is the formal definition of task hardness via the spectrum of the feature covariance matrix $\Lambda$. Specifically, hardness is quantified as $$H(\Lambda) = \operatorname{Tr}(\Lambda)/\lambda_{\min}(\Lambda)$$, which captures the intuition that tasks requiring many weakly represented skills (long-tailed spectra) are harder.

The analysis yields several key results:

• Test-time scaling law: For a fixed test error, increasing the number of CoT steps $k$ at inference allows for a reduction in the number of in-context examples $n$ required during training. This is formalized via explicit error bounds that decay exponentially with $k$, modulated by task hardness.
• Overthinking phenomenon: If the training data does not sufficiently cover the directions (skills) required by the downstream task, increasing test-time compute (longer CoT) can degrade performance, a manifestation of overthinking.
• Resource scaling: The computational complexity at test time scales as $O(kd^2)$, with $d$ the feature dimension.

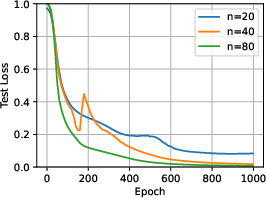
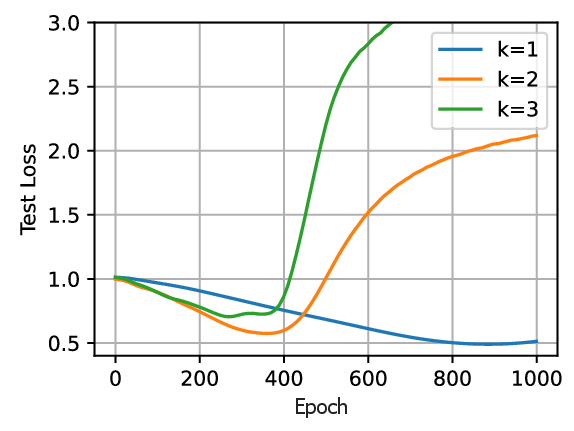
Figure 2: Test error as a function of CoT steps $k$ for different training prompt lengths $n$, illustrating the trade-off between training-time and test-time compute.

Multi-Task Training and Optimal Task Selection

The paper extends the analysis to a multi-task setting, where each task is defined by its own feature covariance. The optimal selection of training tasks is formulated as a quadratic optimization problem, with the objective of minimizing the expected test error on a target task. The analysis reveals that:

• Diversity: The training set should span all directions present in the target task’s covariance to avoid unrepresented skills.
• Relevance: The convex combination of training task covariances should approximate the target task’s covariance.
• Hardness: When the target task is hard (small $\lambda_{\min}$), the optimal selection strategy places significant weight on hard training tasks.

Empirical results confirm that the proposed selection strategy prioritizes hard and diverse tasks, as shown by the distribution of selection probabilities.

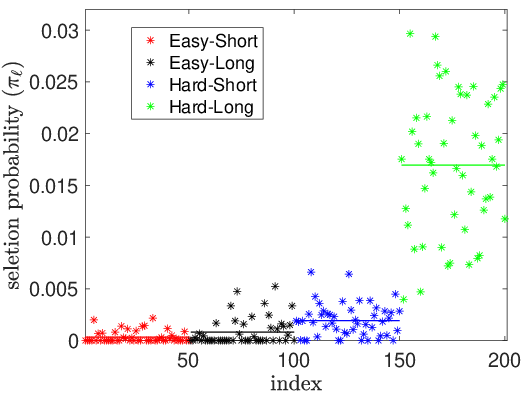
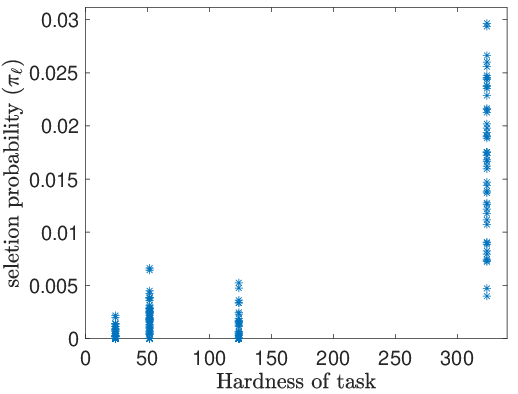
Figure 3: Selection probabilities for different task types, demonstrating that harder and more diverse tasks are favored in the optimal training mixture.

Empirical Validation

Experiments are conducted on both the LSA model and a 12-layer GPT-2 architecture. The results corroborate the theoretical predictions:

• Increasing test-time compute (CoT steps) allows for shorter training prompts without loss in test accuracy, provided the training data covers the relevant skills.
• When the training data is skewed and lacks coverage of certain directions, longer CoT at test time leads to increased error, confirming the overthinking effect.
• The task selection optimization yields mixtures that emphasize hard and diverse tasks, leading to improved generalization on hard target tasks.

Implications and Future Directions

The findings have several practical and theoretical implications:

• Data curation: For effective test-time scaling, training data should be curated to maximize diversity and include hard examples, especially when targeting complex downstream tasks.
• Compute allocation: There is a quantifiable trade-off between training-time and test-time compute, enabling more flexible deployment strategies.
• Limitations: The theoretical results are derived for linear regression and single-layer LSA; extending the analysis to nonlinear data and deeper transformers is a natural next step.

Conclusion

This work provides a principled framework for understanding the interplay between training data properties and test-time scaling in transformer models. By formalizing task hardness and deriving explicit scaling laws, it clarifies when and why additional test-time compute is beneficial or detrimental. The results inform both the design of training curricula and the deployment of inference-time reasoning strategies, with direct implications for the development of more robust and adaptable AI systems.