Why Do We Need Warm-up? A Theoretical Perspective (2510.03164v1)

Abstract: Learning rate warm-up - increasing the learning rate at the beginning of training - has become a ubiquitous heuristic in modern deep learning, yet its theoretical foundations remain poorly understood. In this work, we provide a principled explanation for why warm-up improves training. We rely on a generalization of the $(L_0, L_1)$-smoothness condition, which bounds local curvature as a linear function of the loss sub-optimality and exhibits desirable closure properties. We demonstrate both theoretically and empirically that this condition holds for common neural architectures trained with mean-squared error and cross-entropy losses. Under this assumption, we prove that Gradient Descent with a warm-up schedule achieves faster convergence than with a fixed step-size, establishing upper and lower complexity bounds. Finally, we validate our theoretical insights through experiments on language and vision models, confirming the practical benefits of warm-up schedules.

• The paper introduces the (H0, H1)-smoothness condition linking loss sub-optimality and local curvature to justify the effectiveness of LR warm-up.
• The paper demonstrates that adaptive warm-up schedules achieve provably faster convergence than fixed step-size, validated through experiments on LLMs and vision models.
• The paper provides practical insights for optimizing training, emphasizing the balance between warm-up length, peak learning rates, and overall model performance.

Theoretical Foundations and Practical Implications of Learning Rate Warm-up

Introduction

The paper "Why Do We Need Warm-up? A Theoretical Perspective" (2510.03164) provides a rigorous theoretical framework for understanding the empirical success of learning rate (LR) warm-up in deep learning optimization. The authors introduce the $(H_0, H_1)$-smoothness condition, which bounds the local curvature of the loss landscape as a linear function of the loss sub-optimality, and demonstrate both theoretically and empirically that this condition holds for common neural architectures and loss functions. The work establishes that gradient descent (GD) with a warm-up schedule achieves provably faster convergence than with a fixed step-size, and validates these findings with experiments on LLMs and vision transformers.

The $(H_0, H_1)$-Smoothness Condition

The central theoretical contribution is the $(H_0, H_1)$-smoothness condition, defined as:

$\|\nabla^2 f(w)\|_2 \leq H_0 + H_1(f(w) - f^*)$

where $f^*$ is the global minimum of the loss function. This condition generalizes the previously studied $(L_0, L_1)$-smoothness, which bounds the Hessian norm by a function of the gradient norm. The $(H_0, H_1)$-smoothness is shown to be strictly more general, possessing closure under finite sums and affine transformations—properties essential for modeling the composite loss landscapes of deep neural networks.

Theoretical justification is provided for deep linear and non-linear networks under balancedness and L2 regularization, with explicit bounds for $H_0$ and $H_1$ derived for architectures with MSE and cross-entropy losses. The authors also show that $(L_0, L_1)$-smoothness fails to hold for simple two-layer networks under these regularization schemes, highlighting the necessity of the $(H_0, H_1)$ framework.

Empirical Verification of $(H_0, H_1)$-Smoothness

Empirical analysis confirms that the $(H_0, H_1)$-smoothness condition accurately models the relationship between local curvature and loss sub-optimality in practical settings. Experiments on transformer-based LLMs (70M, 160M, 410M parameters) trained on the FineWeb dataset with SGD at a small constant LR show a linear decay of estimated local smoothness with training loss throughout early training.

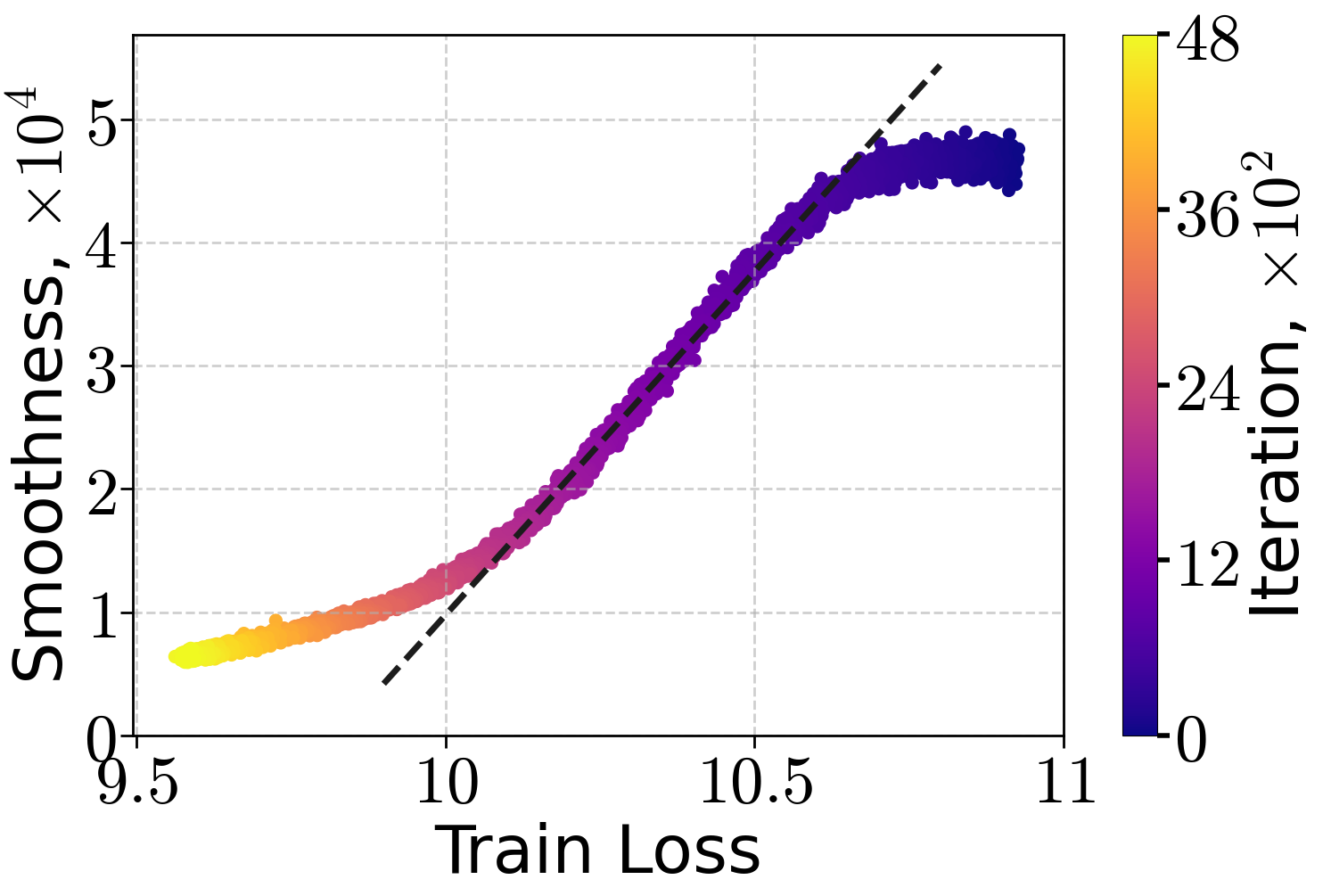
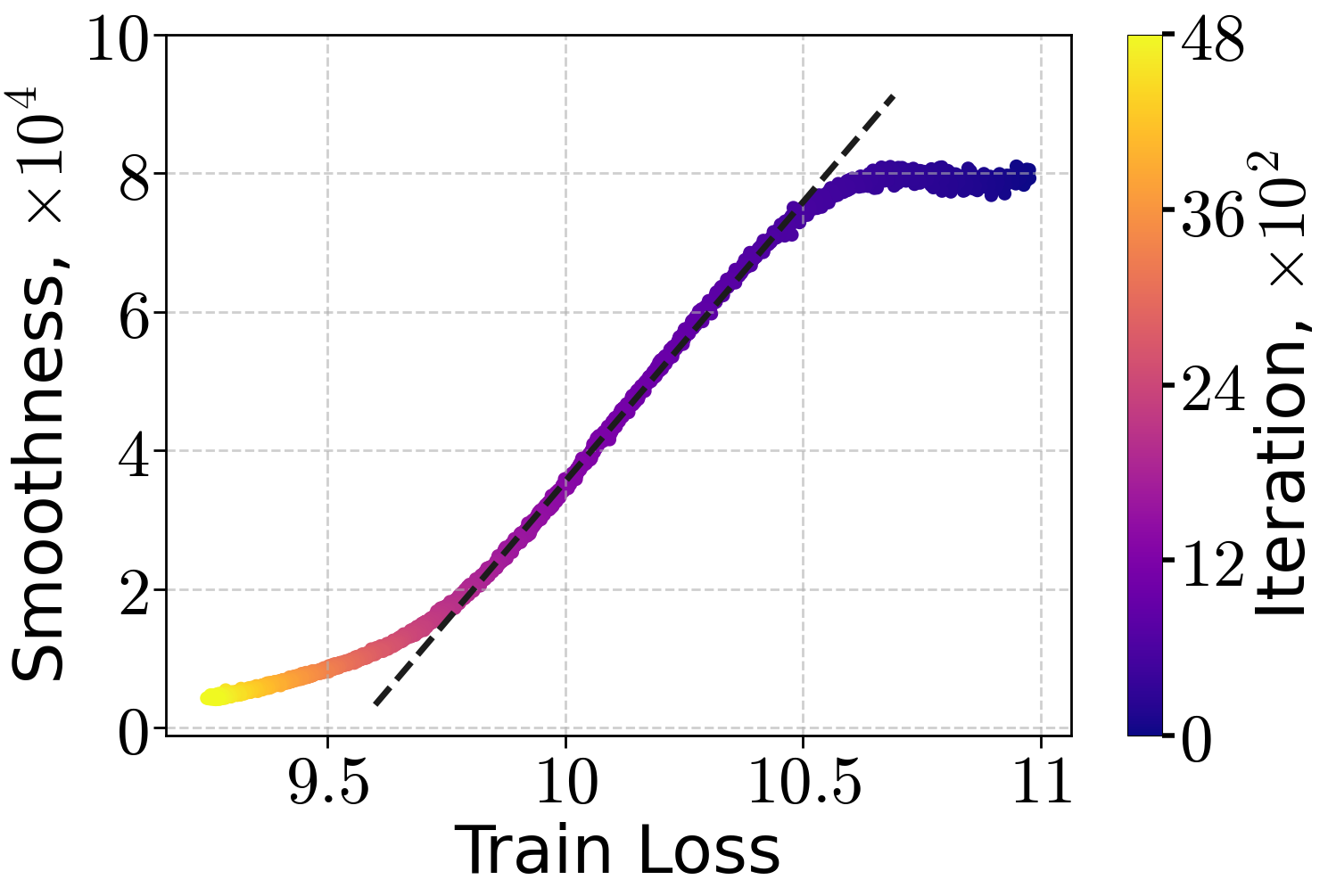
Figure 1: Local smoothness approximation versus training loss for LLMs of varying sizes on the FineWeb dataset, using SGD.

Similar trends are observed for ResNet50 and ViT-Tiny models on ImageNet32, though with higher variance in the smoothness-loss relationship.

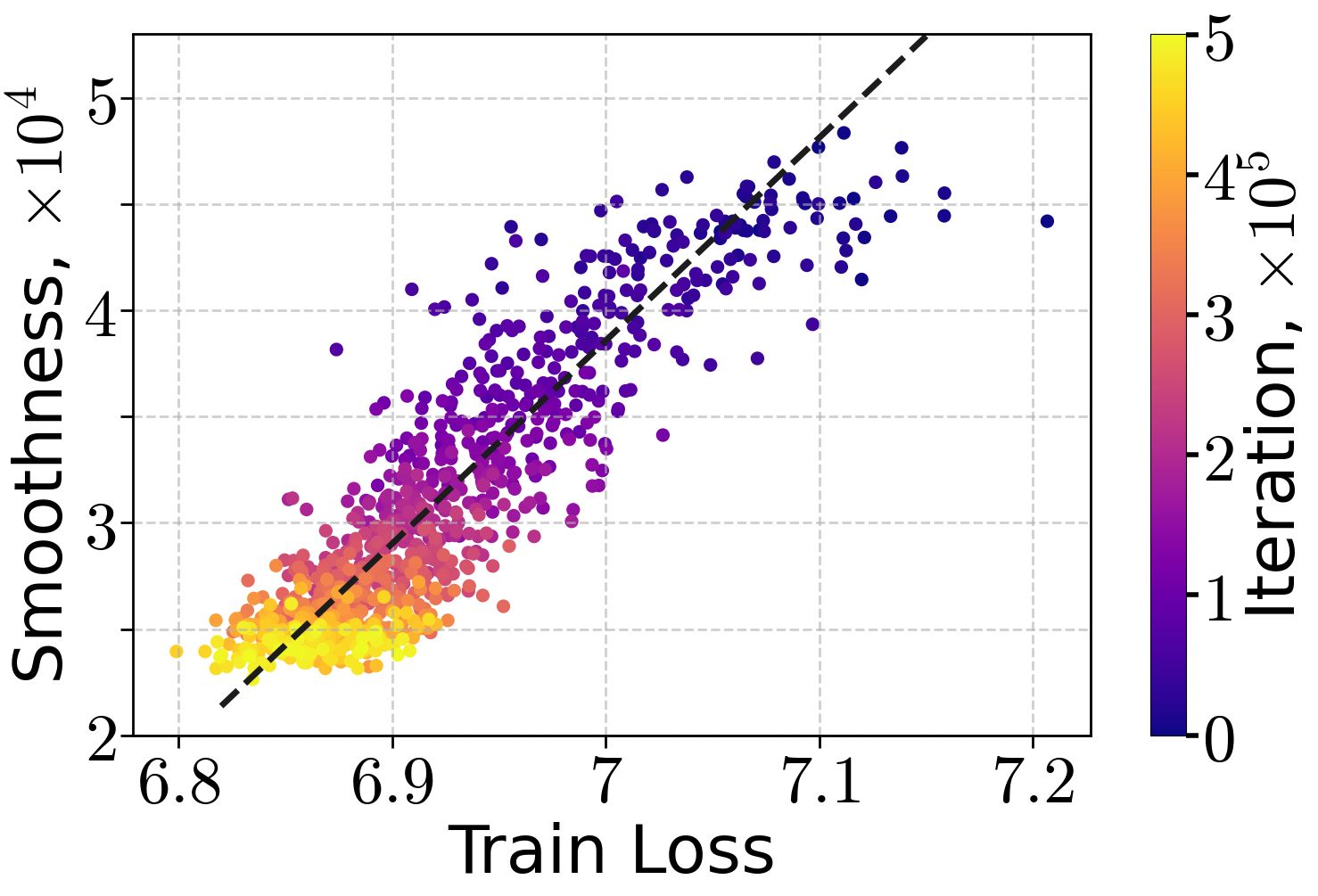
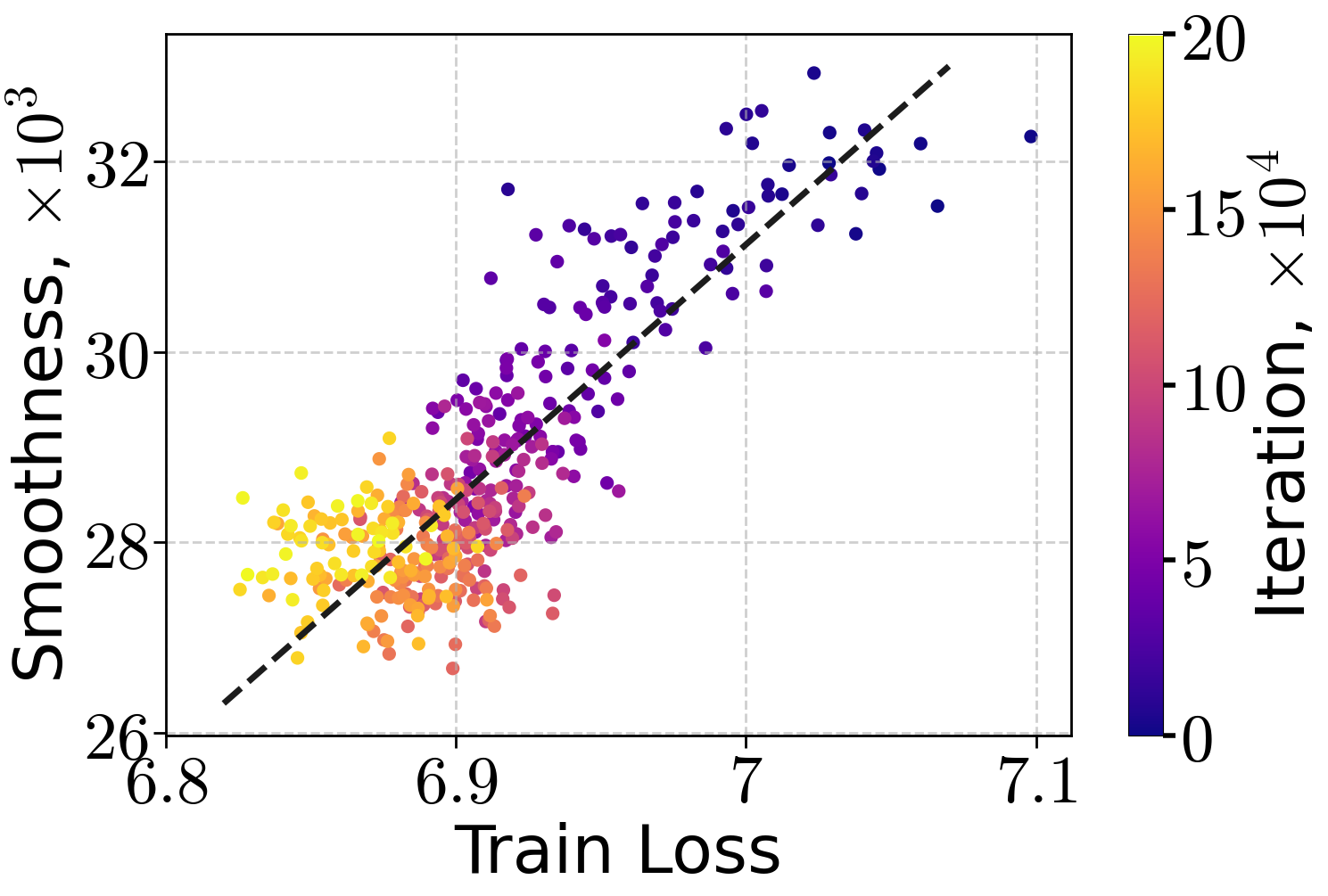
Figure 2: Local smoothness approximation against train loss during training a ResNet50 (left) and ViT-Tiny (right) on ImageNet32, using SGD.

These results support the use of $(H_0, H_1)$-smoothness as a practical tool for analyzing and designing optimization schedules in deep learning.

Convergence Analysis: Warm-up vs. Fixed Step-size

The authors rigorously analyze the convergence of GD under $(H_0, H_1)$-smoothness, comparing adaptive warm-up schedules to fixed step-size strategies. They prove lower complexity bounds for fixed step-size GD, showing that the number of iterations required to reach a given accuracy is substantially higher when the initialization is poor or high precision is needed.

For GD with an adaptive warm-up schedule:

$\eta_k = \frac{1}{10H_0 + 20H_1(f(w_k) - f^*)}$

theoretical results show that convergence is significantly accelerated, especially when $H_1(f(w_0)-f^*)/\varepsilon$ is large. This is formalized for both the Aiming condition and Polyak-Łojasiewicz (PL) functions, which are relevant for over-parameterized networks and convex-like regions of the loss landscape.

Stochastic Setting and Interpolation

The analysis is extended to stochastic gradient descent (SGD) under the interpolation condition, which is typical for over-parameterized models. The authors prove that the expected sub-optimality converges at a rate determined by $H_0$, with the failure probability vanishing as the number of iterations increases.

Experimental Validation: Language and Vision Models

Extensive experiments validate the theoretical findings. The $(H_0, H_1)$-driven warm-up schedule is compared to linear and no warm-up across LLMs and ViT models. Both $(H_0, H_1)$ and linear warm-up yield superior training and validation performance compared to no warm-up, with $(H_0, H_1)$ warm-up matching or exceeding linear warm-up when the schedule parameter $C$ is properly tuned.

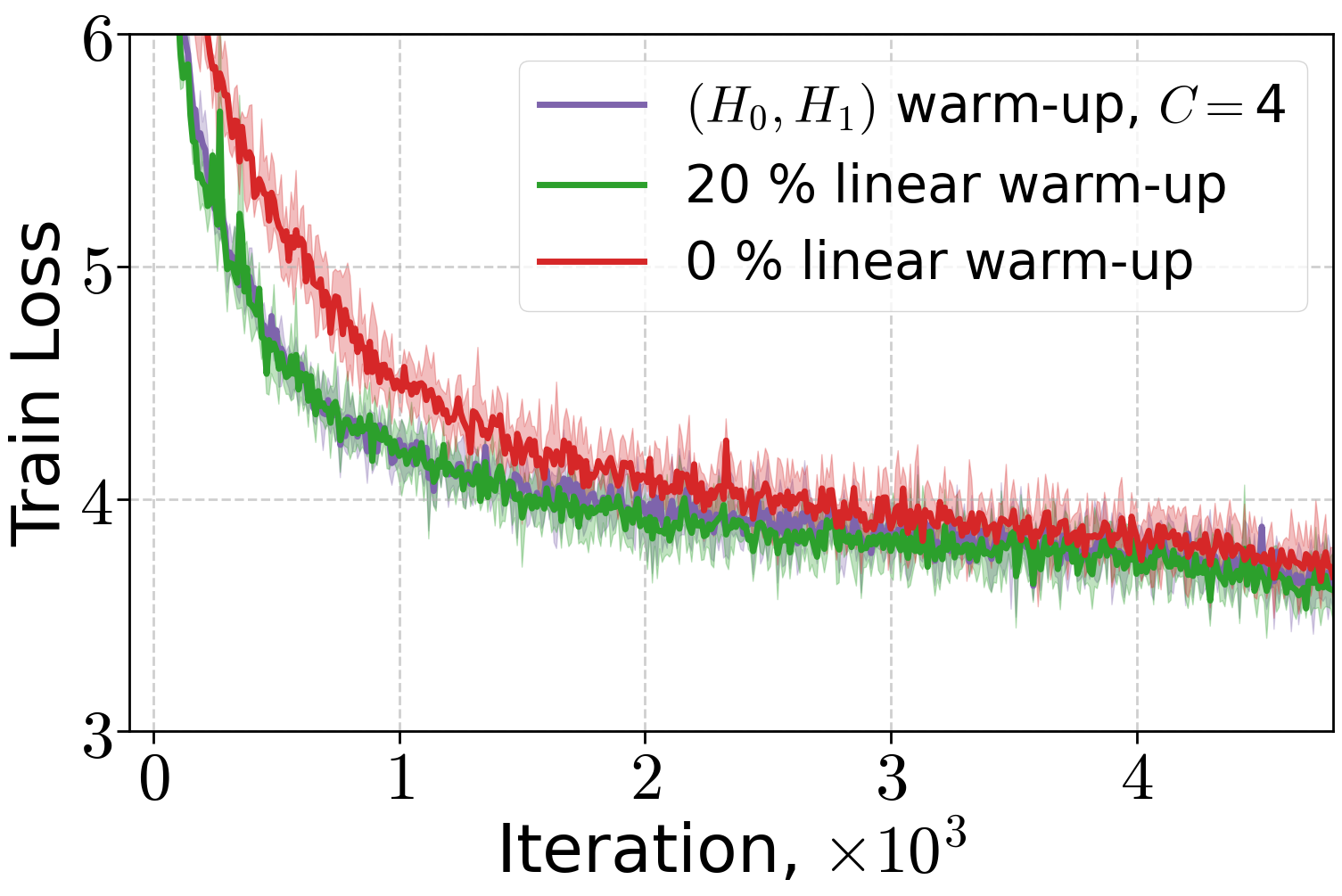
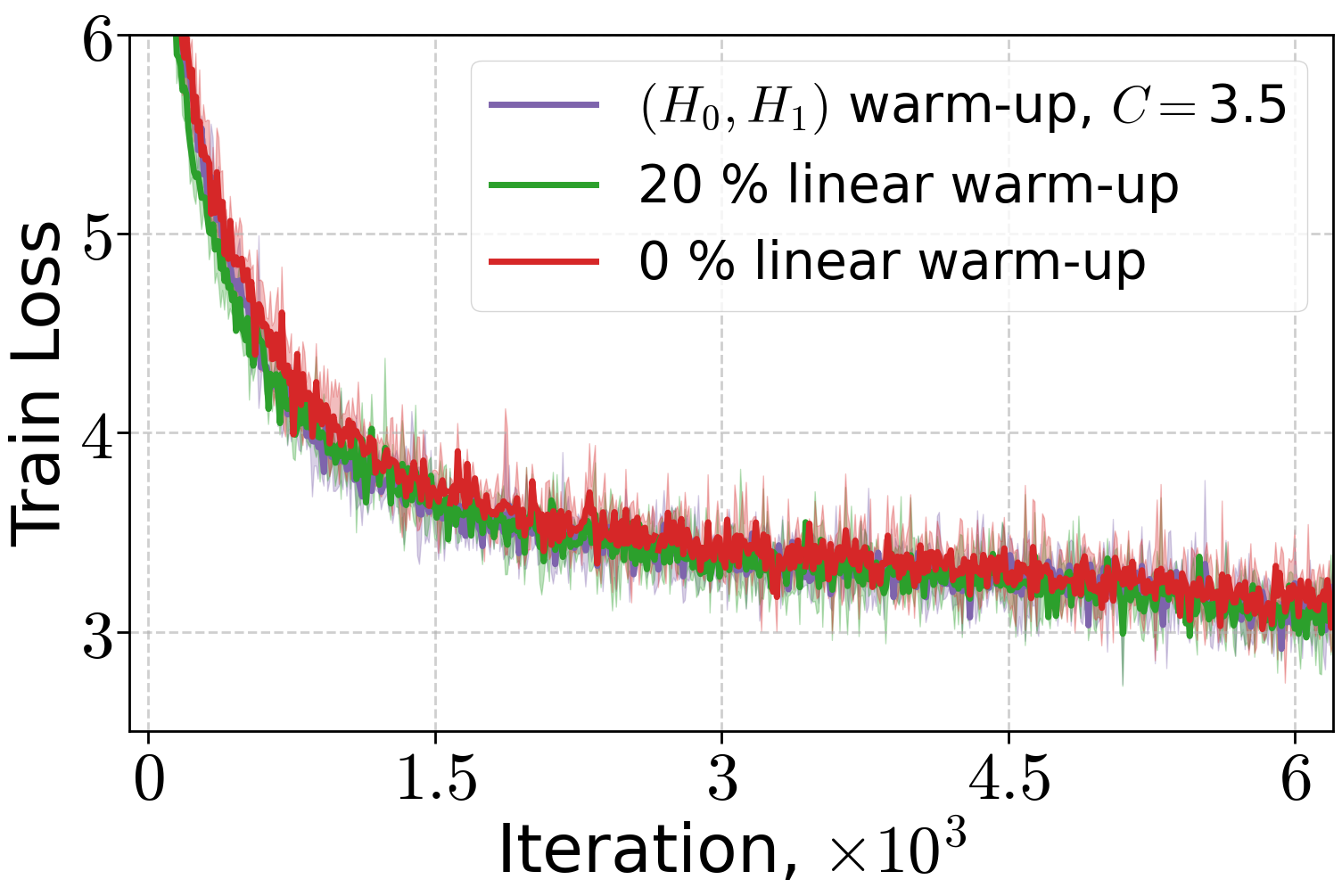
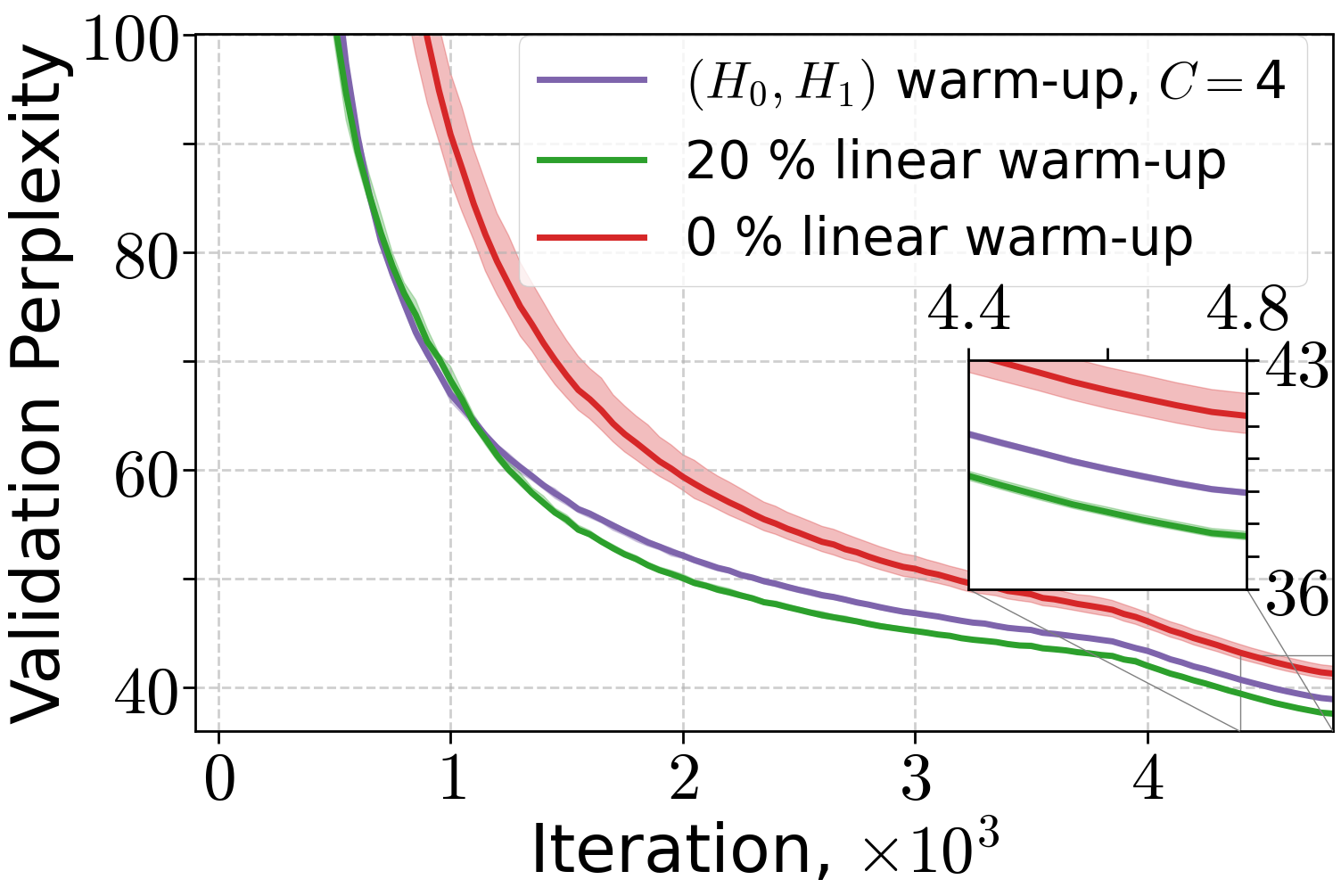
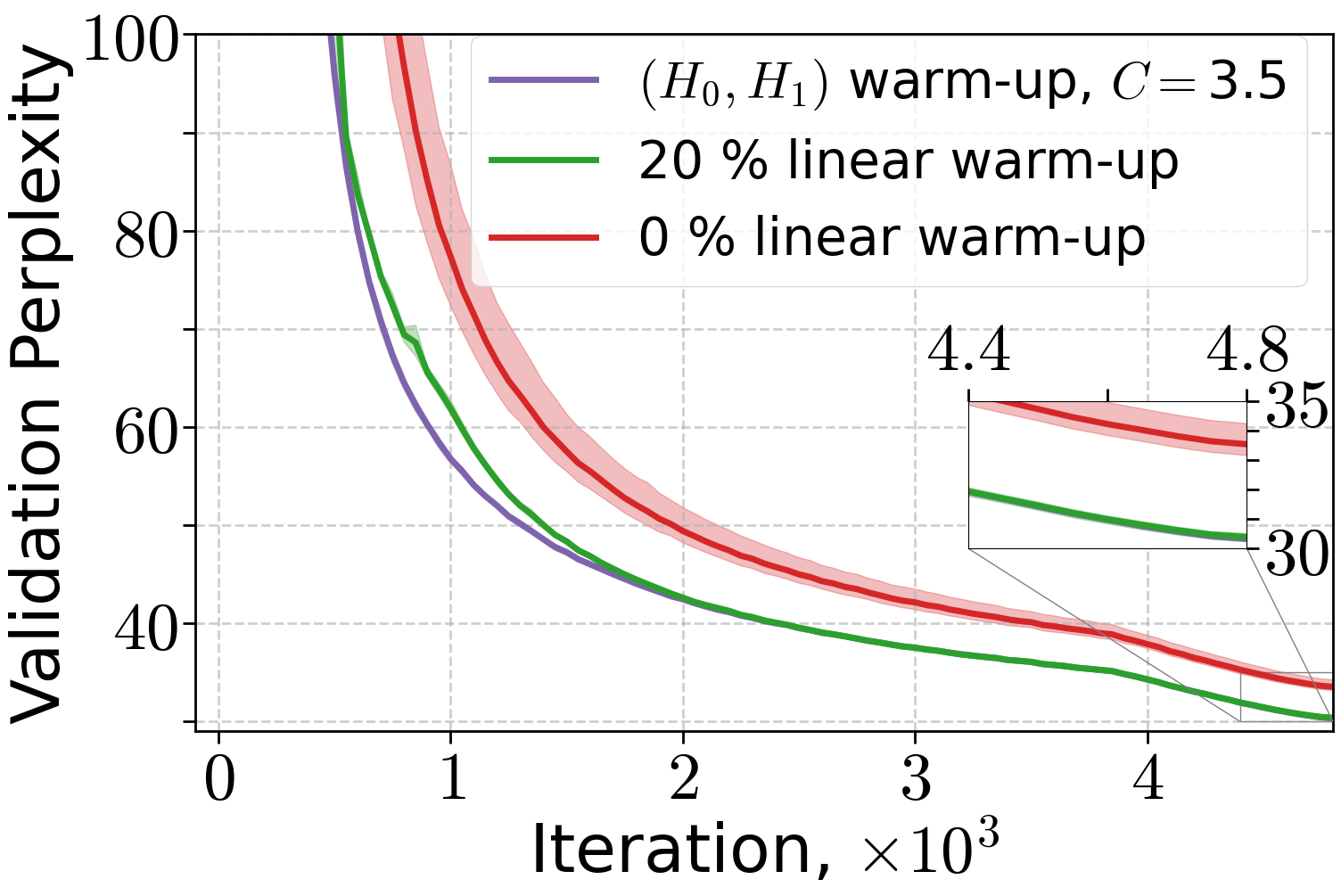
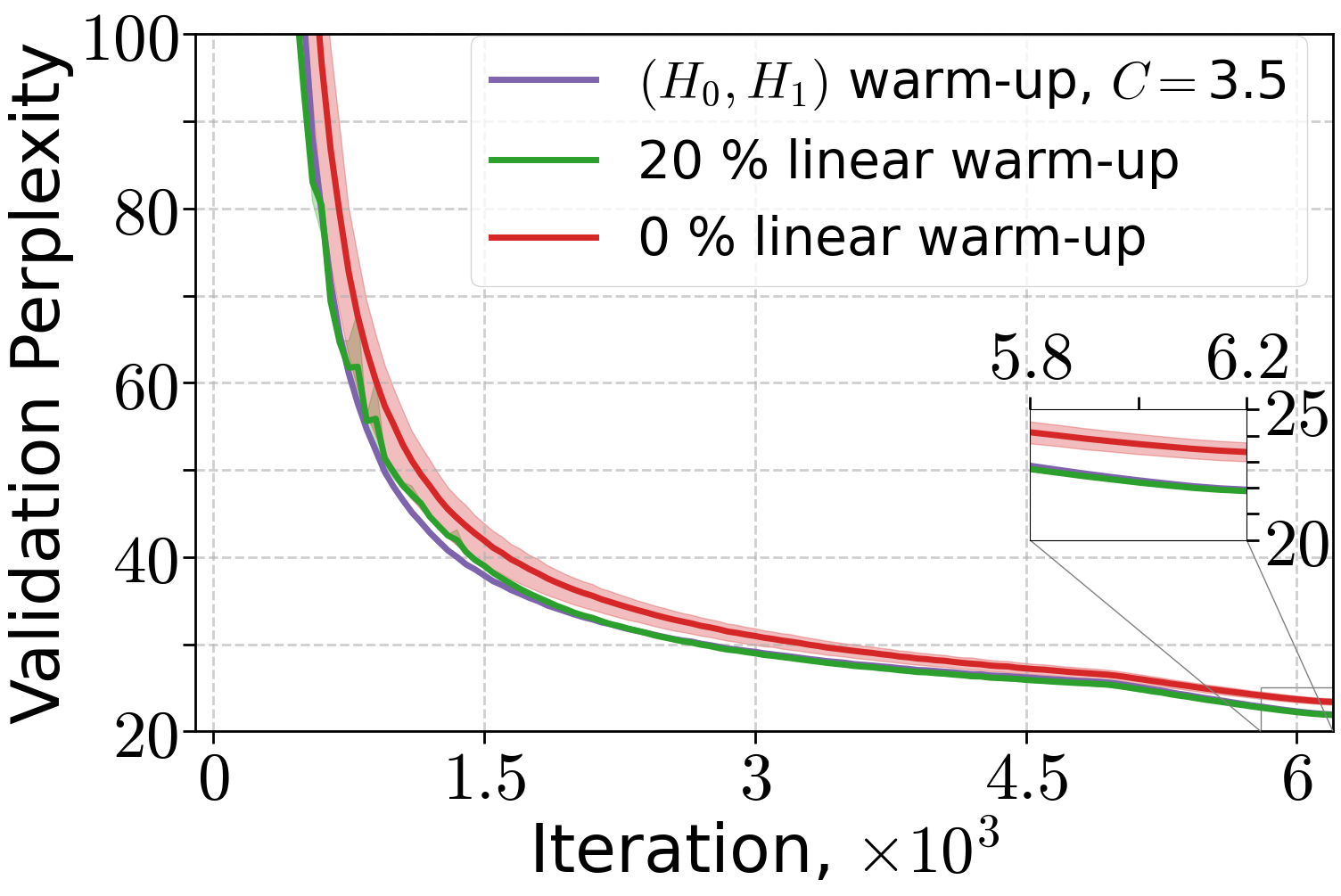
Figure 3: Performance of Adam optimizer for 70M and 160M LLMs and AdamW for 410M LLMs under different warm-up strategies.

The effective learning rate profiles for $(H_0, H_1)$ warm-up differ substantially from linear warm-up, reflecting the theoretical prescription.

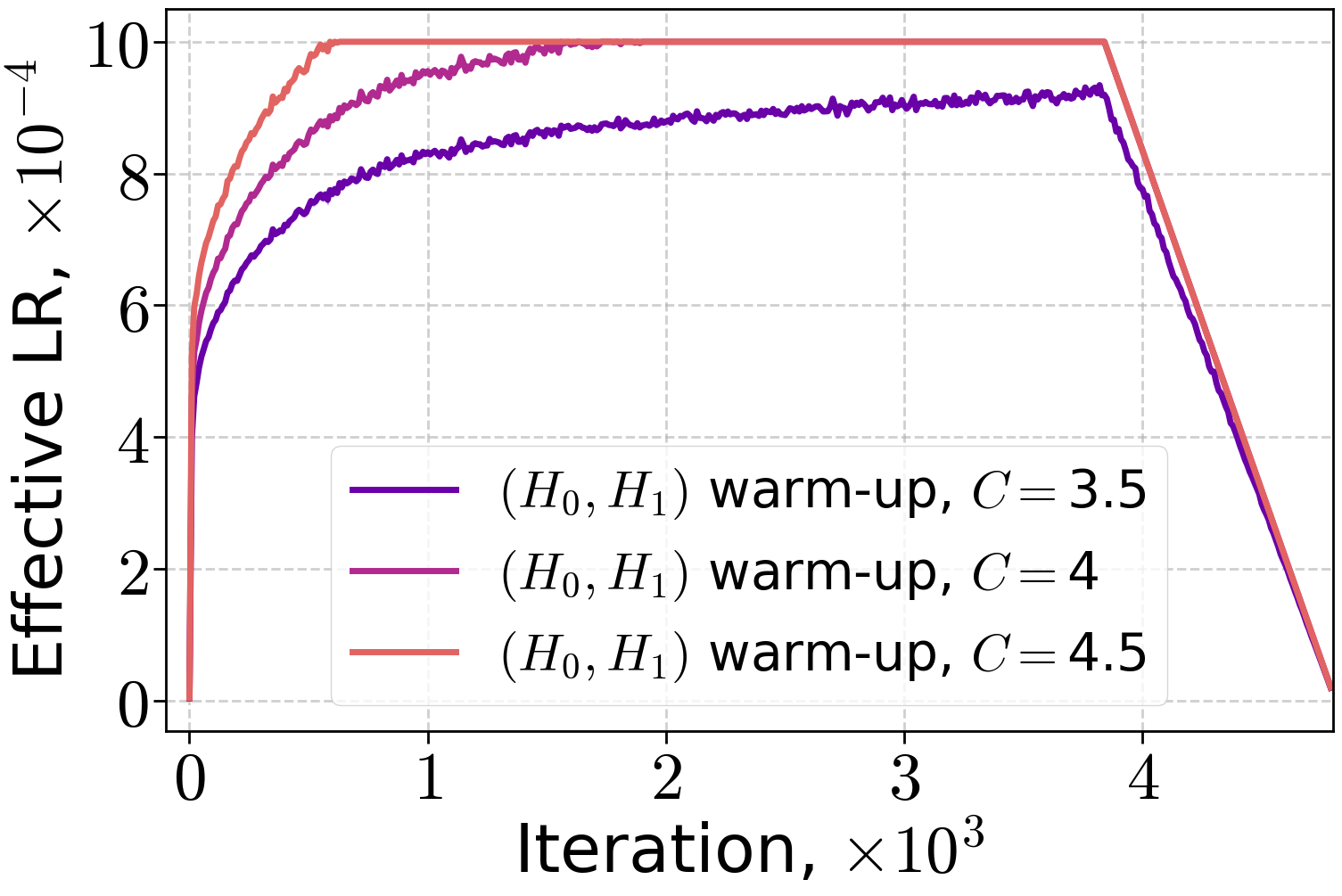
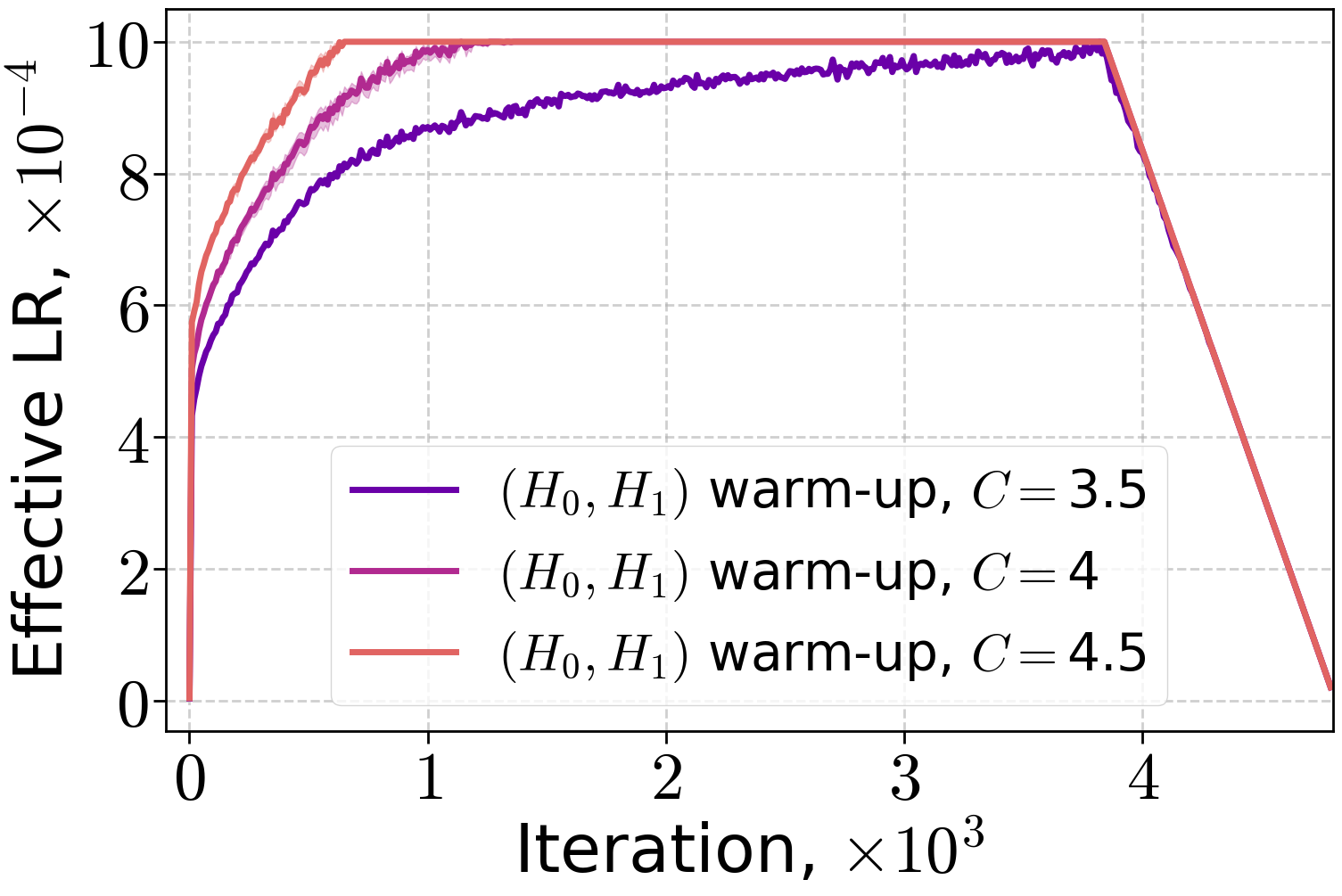
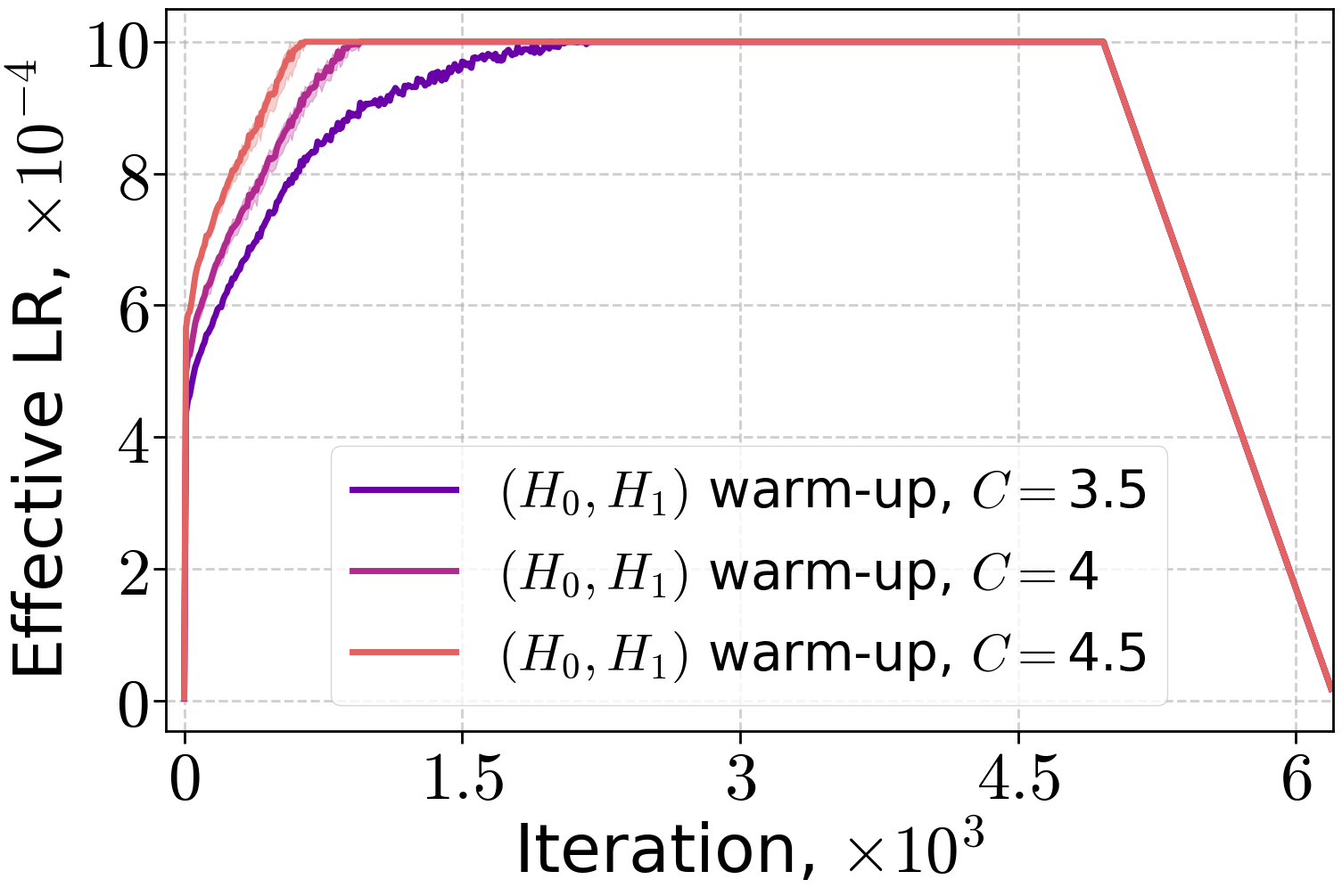
Figure 4: Effective LR with $(H_0, H_1)$ warm-up when training LLMs on the FineWeb dataset for the peak LR $10^{-3}$.

Similar results are obtained for ViT-Tiny on ImageNet32, with both warm-up strategies outperforming no warm-up.

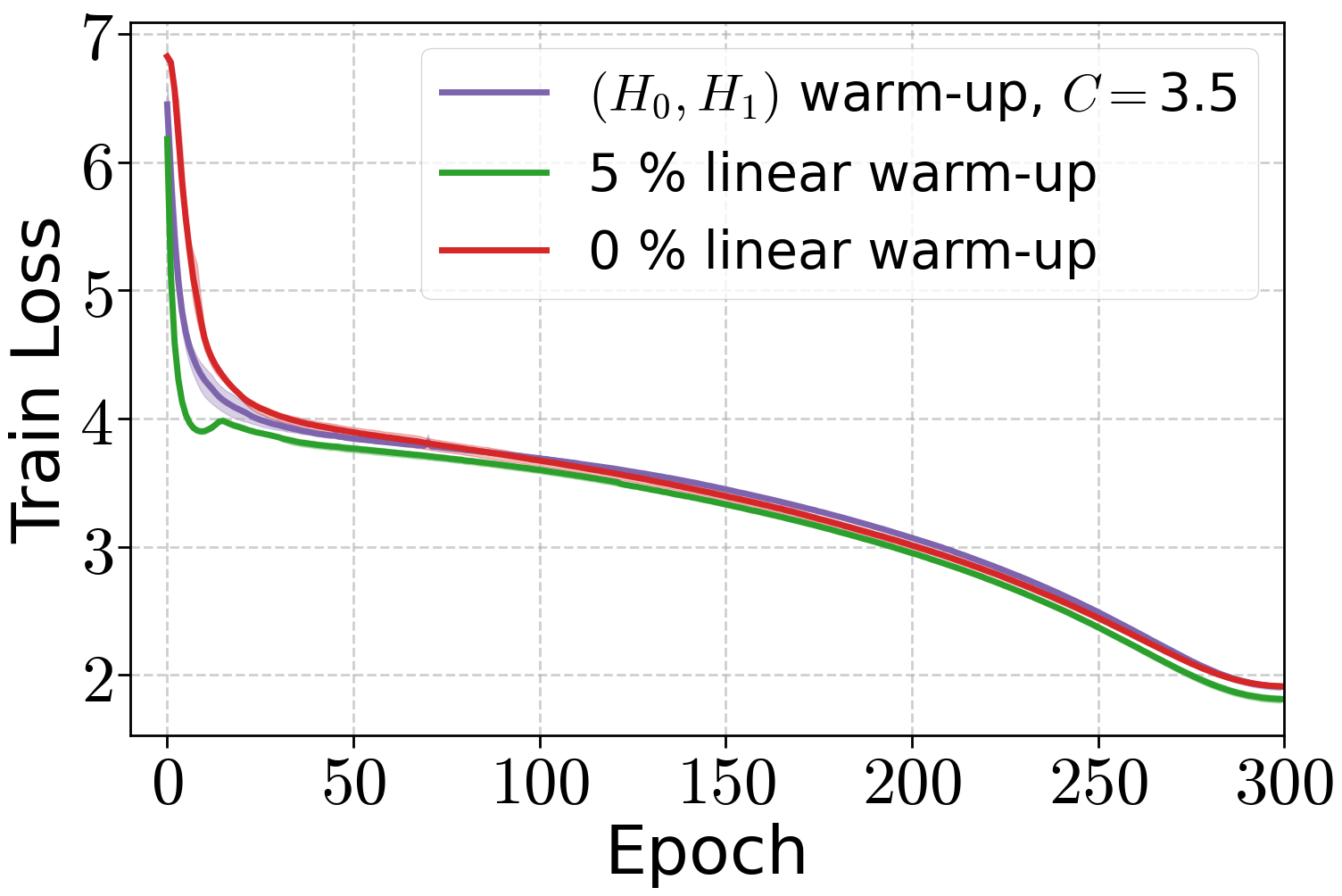
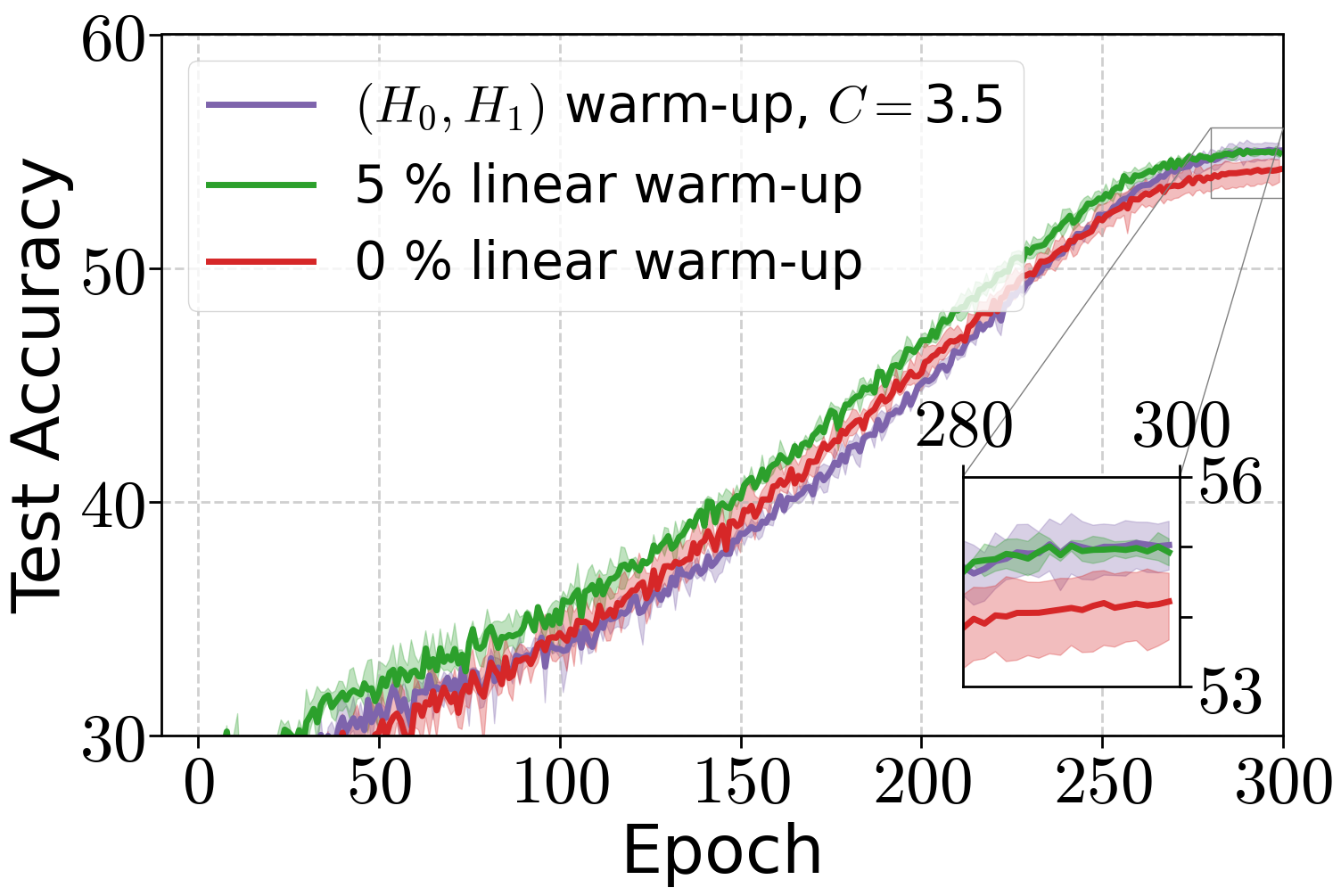
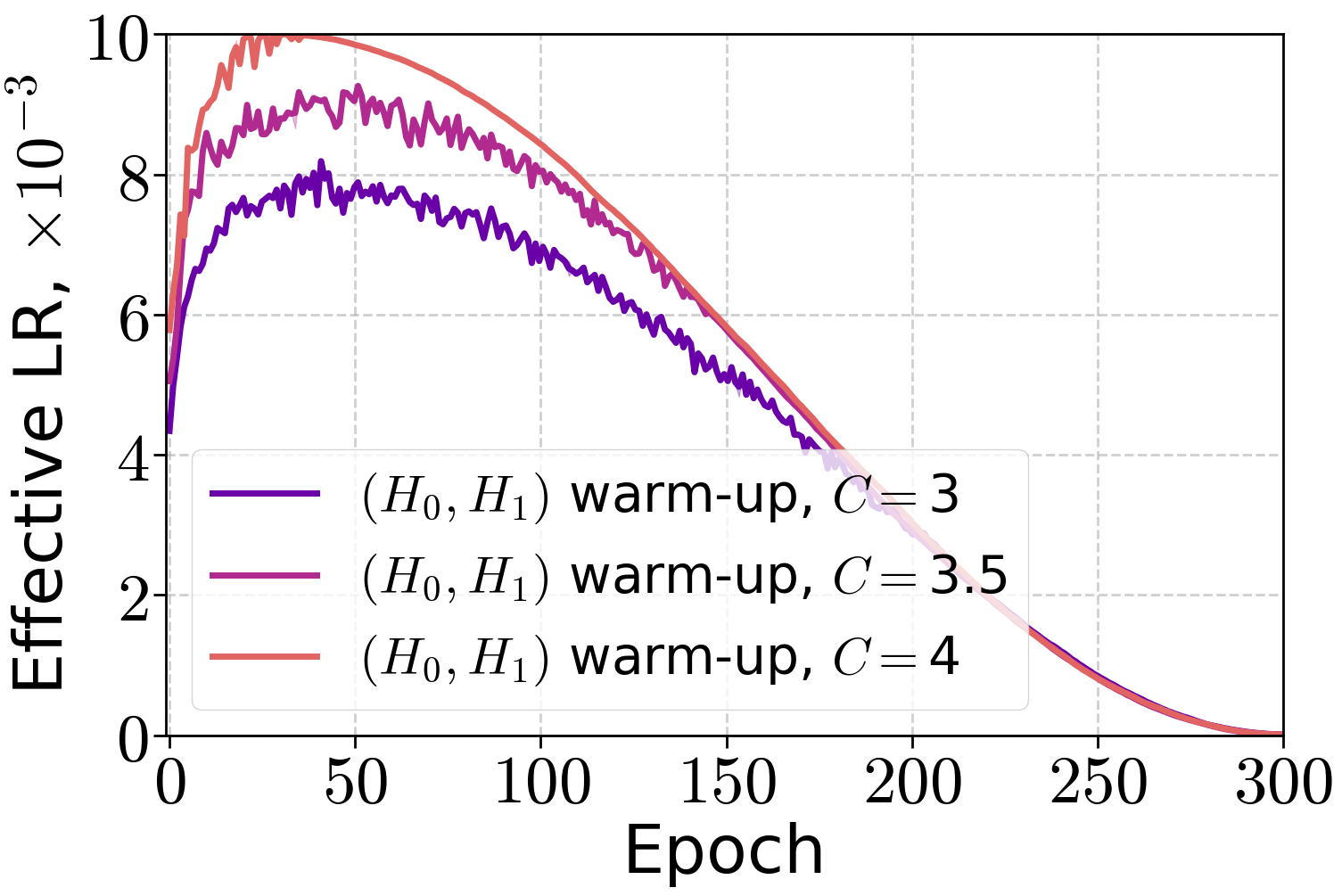
Figure 5: Performance of AdamW with weight decay when training ViT model on ImageNet32 with different warm-up strategies.

Ablation Studies

Ablation studies on warm-up length and peak learning rate demonstrate that both $(H_0, H_1)$ and linear warm-up schedules are robust to hyperparameter choices, with $(H_0, H_1)$ warm-up enabling convergence at higher peak LRs for smaller models. For larger models, linear warm-up is more robust to peak LR selection, but $(H_0, H_1)$ warm-up can match its performance when properly tuned.

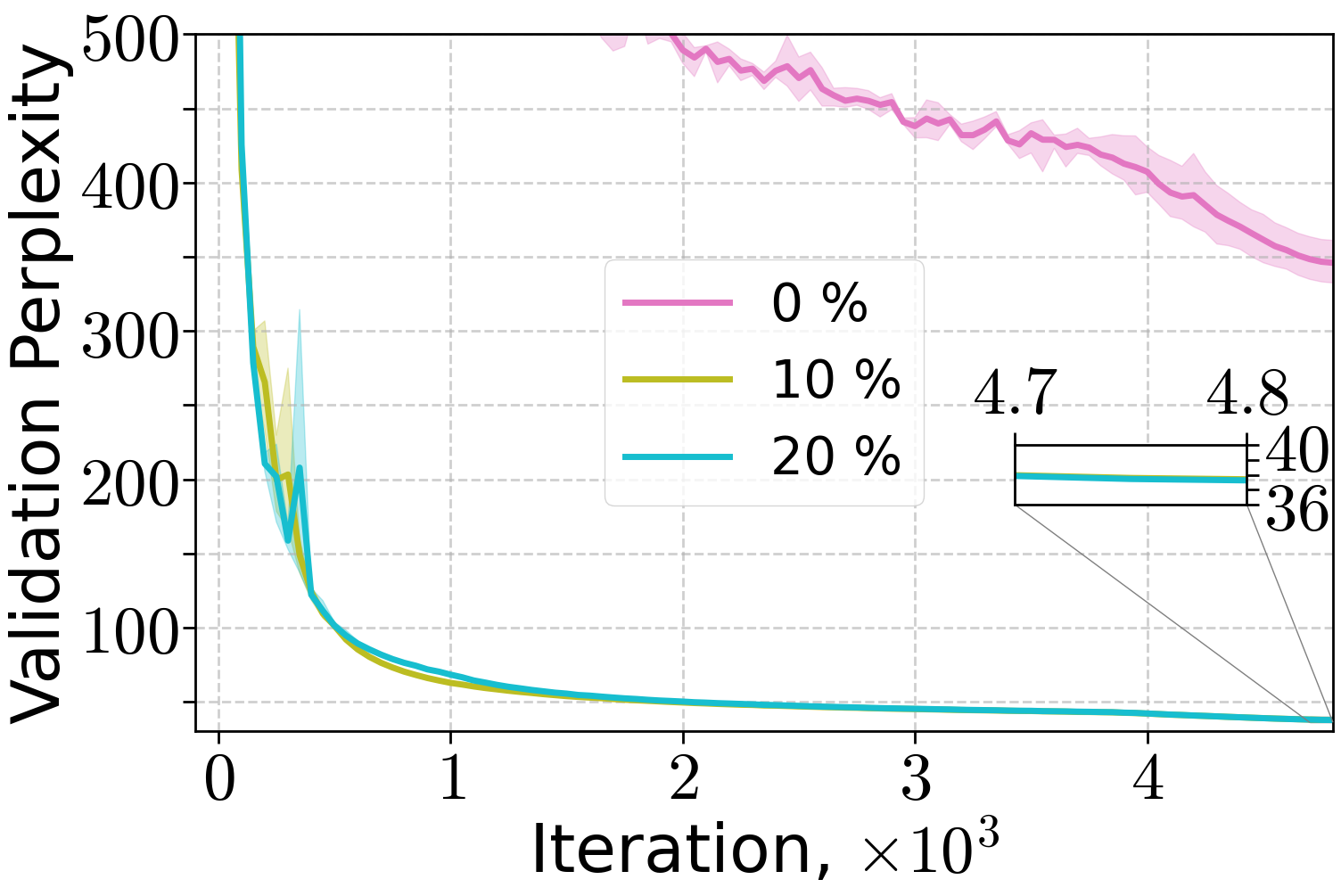
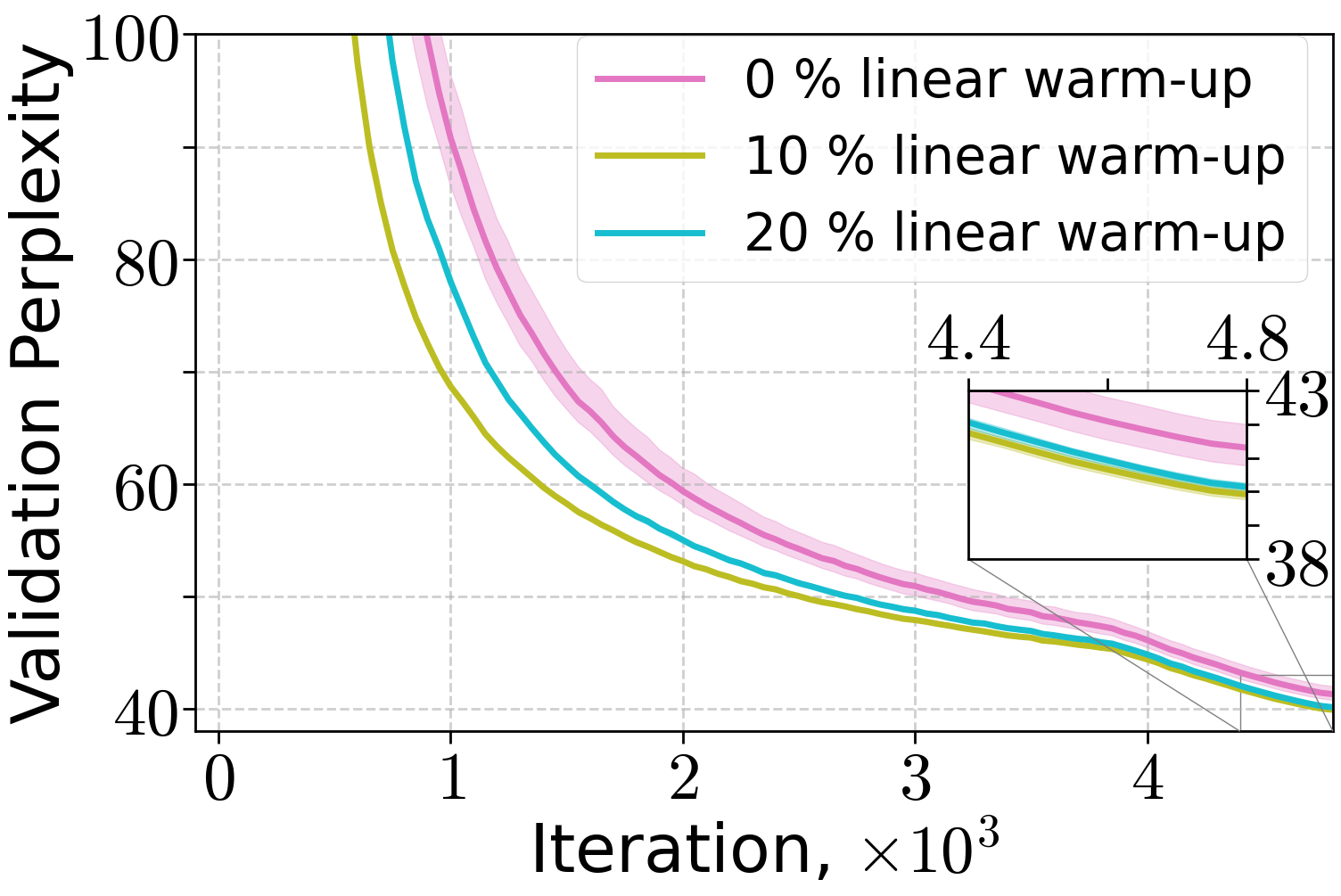
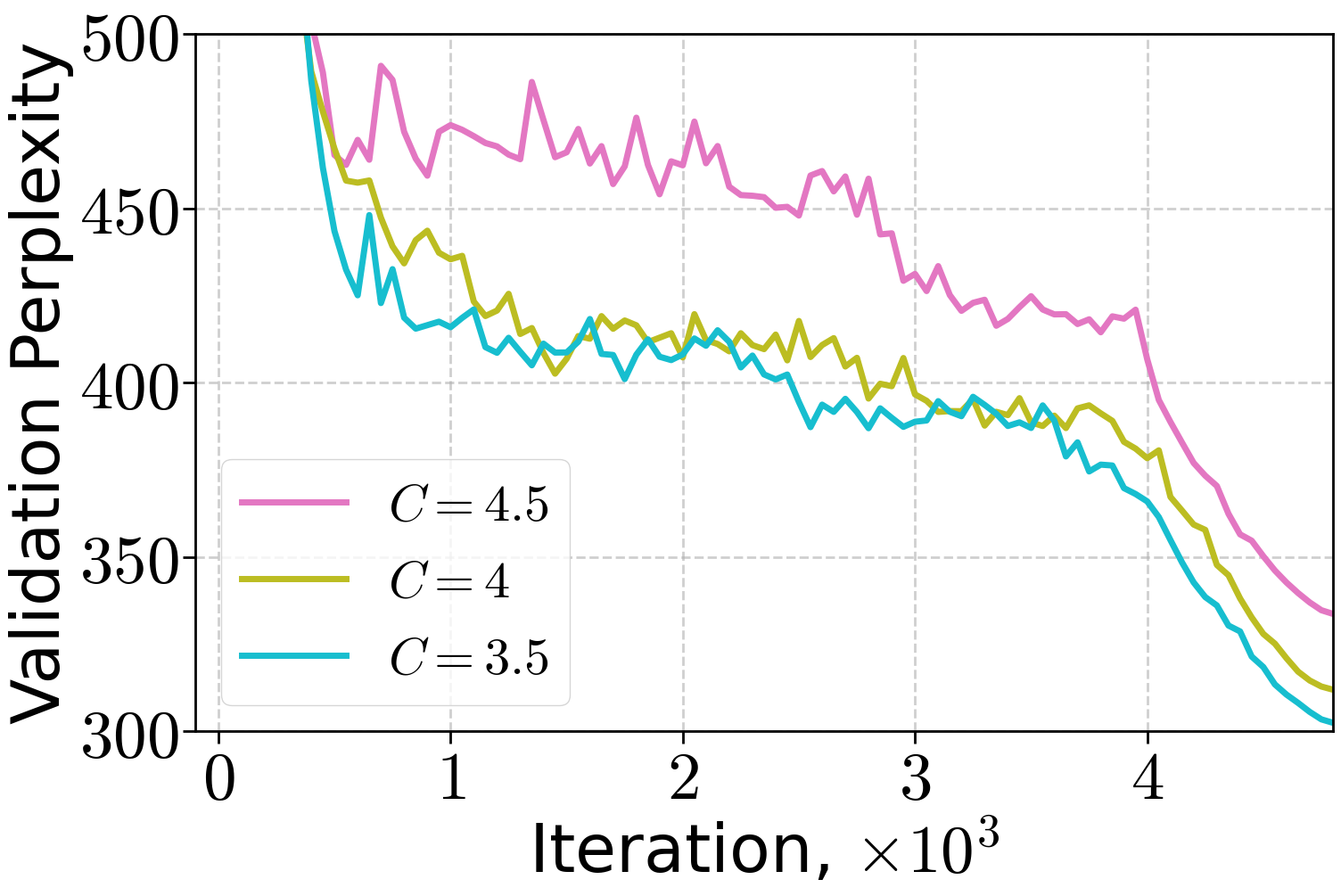
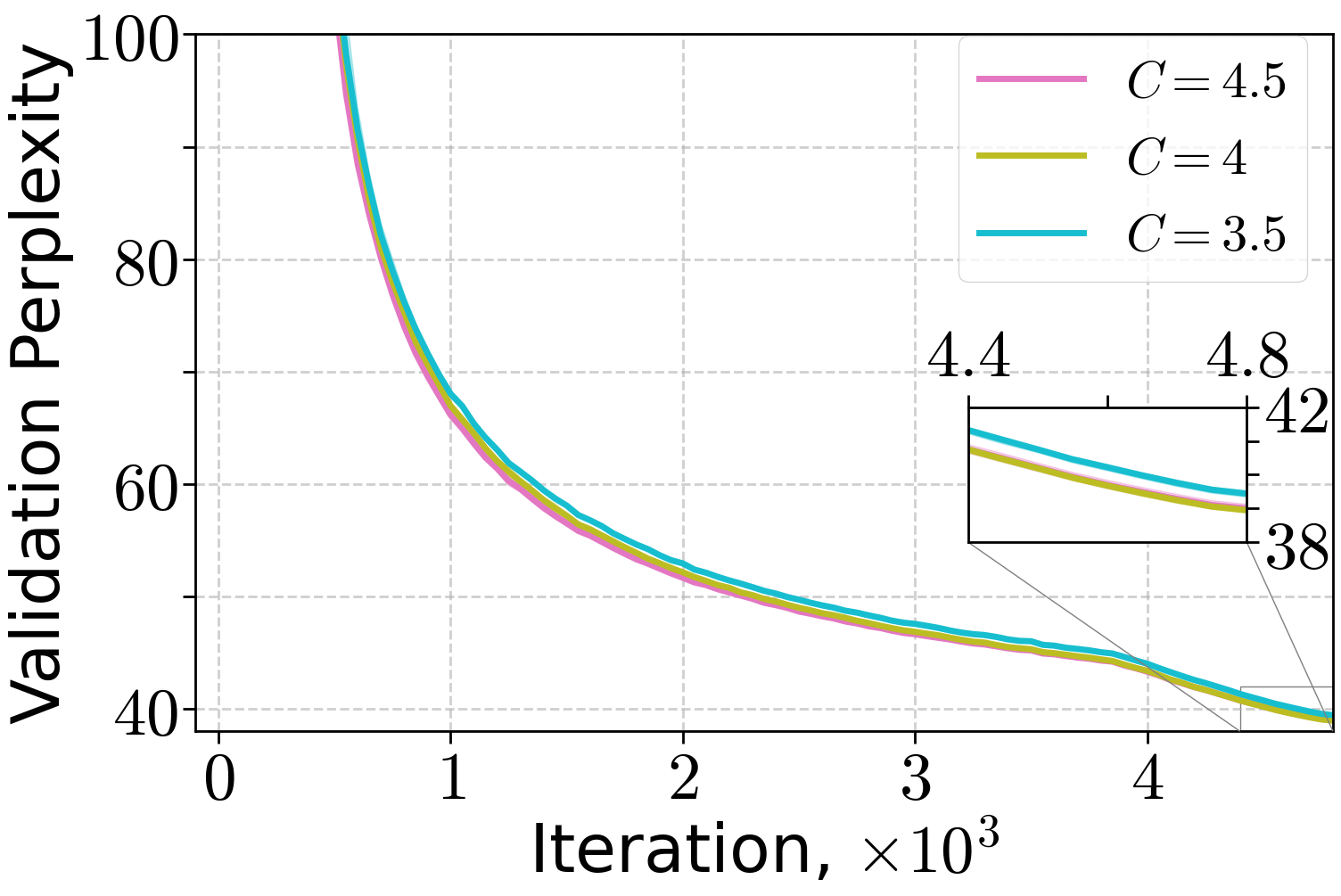
Figure 6: Training of 70M LLM on FineWeb dataset varying the length of linear warm-up and threshold $C$ of $(H_0, H_1)$ warm-up for the peak learning rate $10^{-2}$.

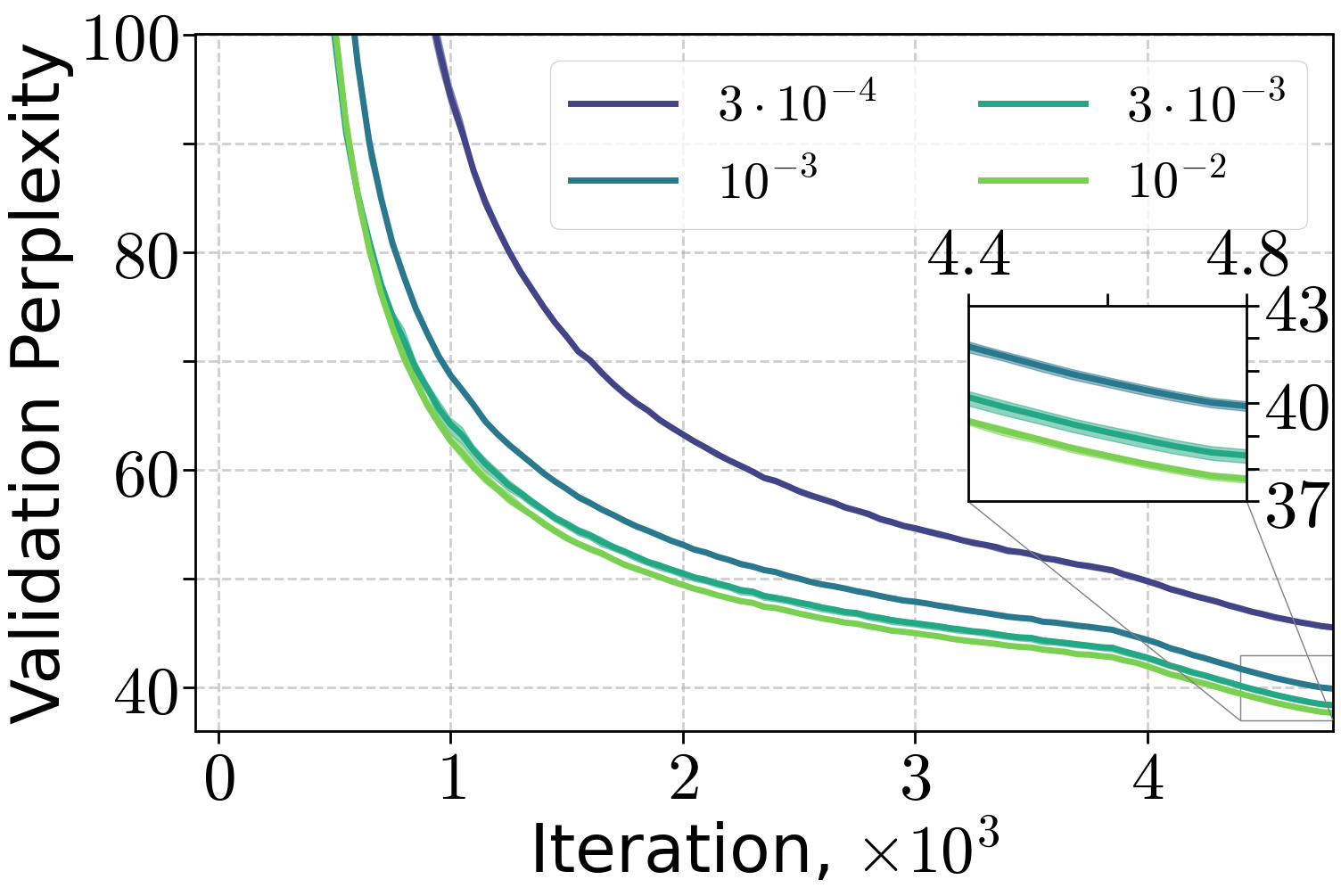
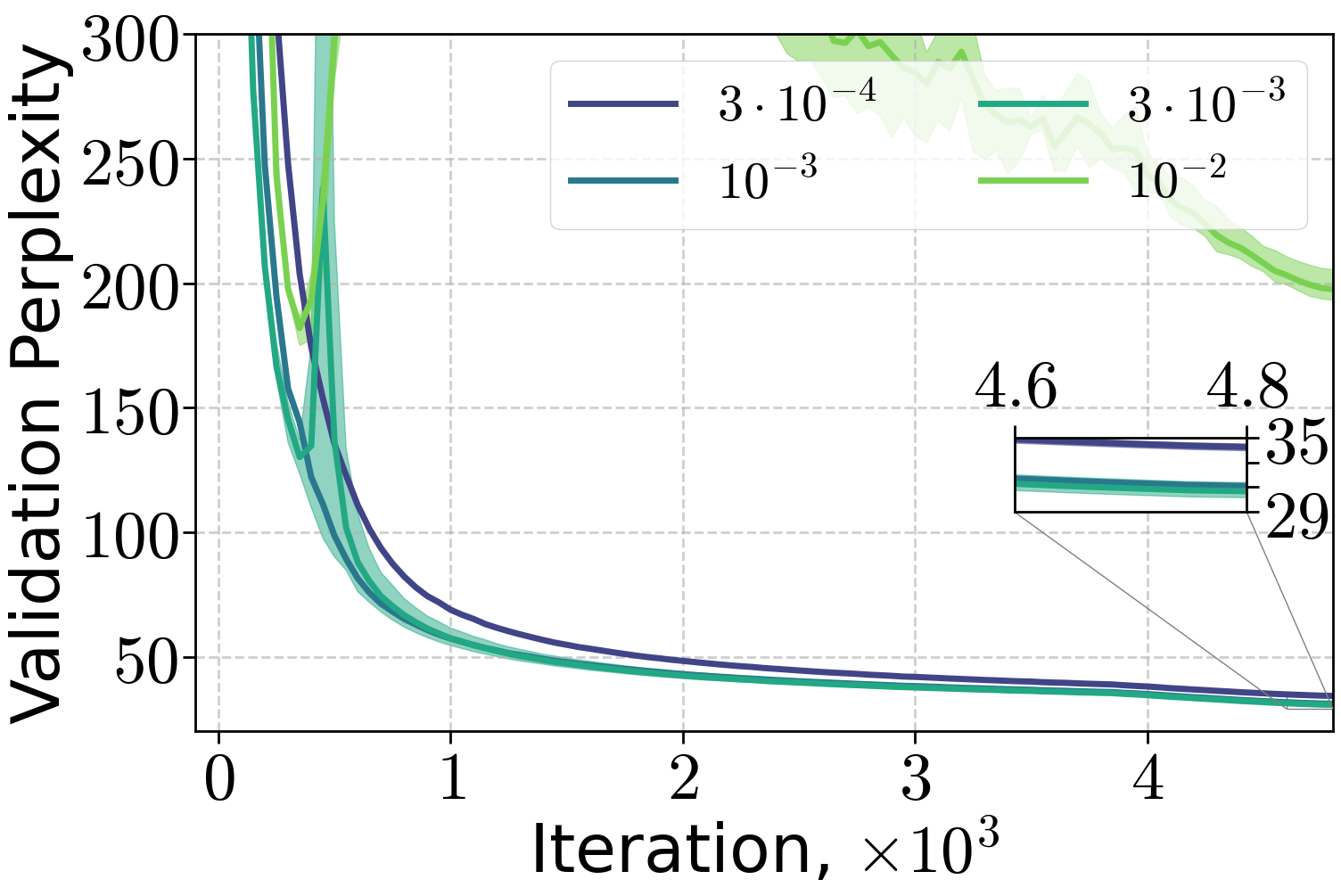
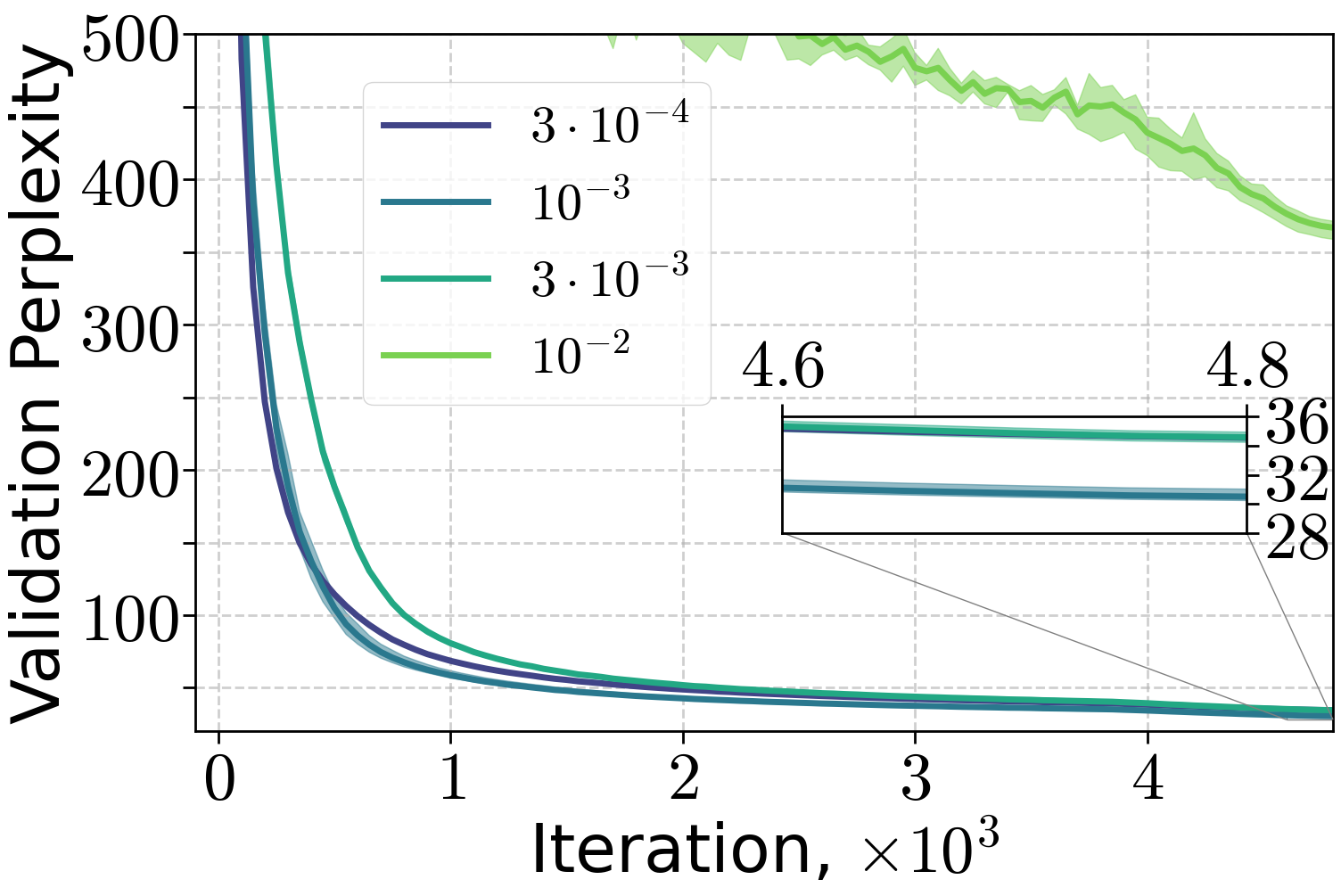
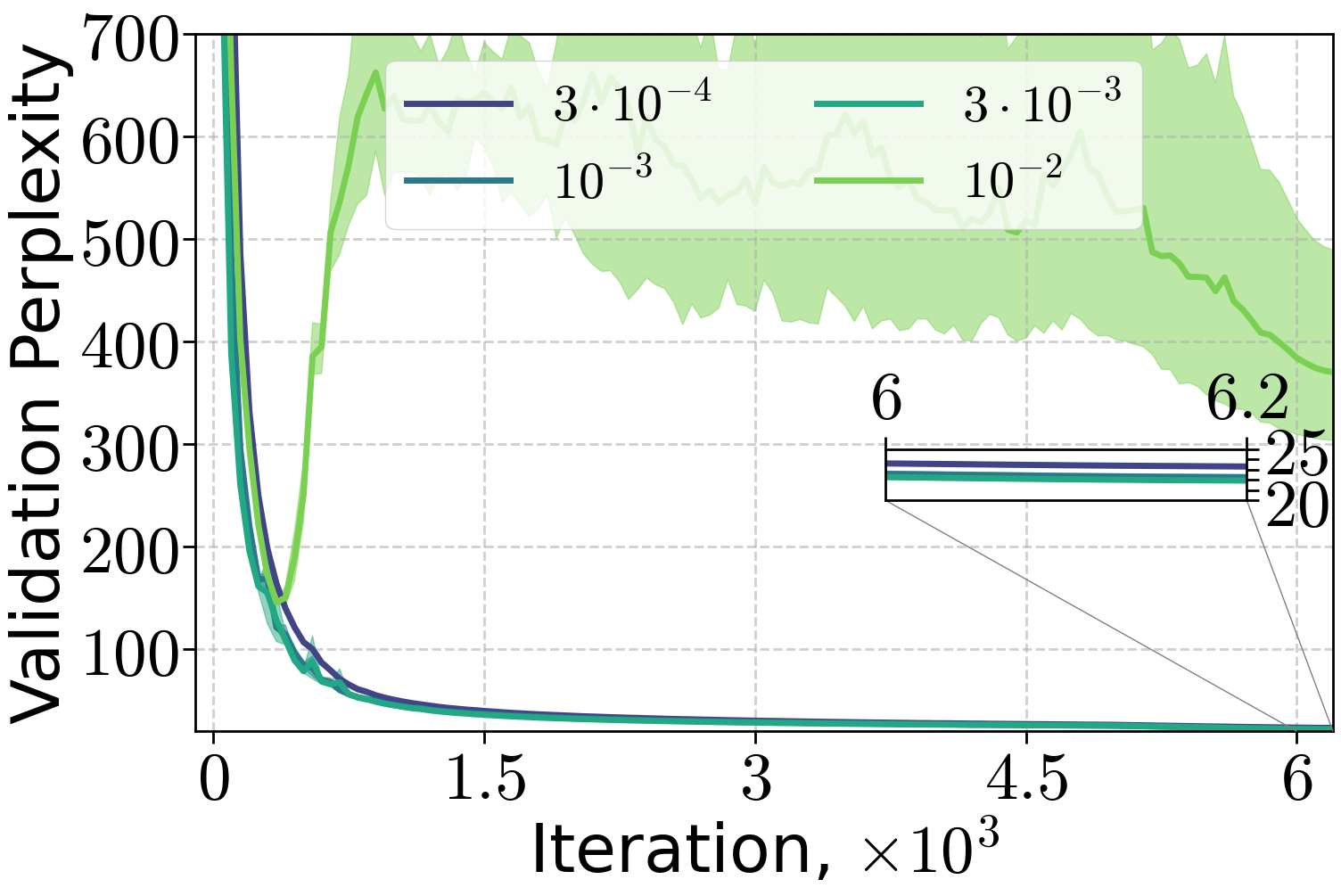
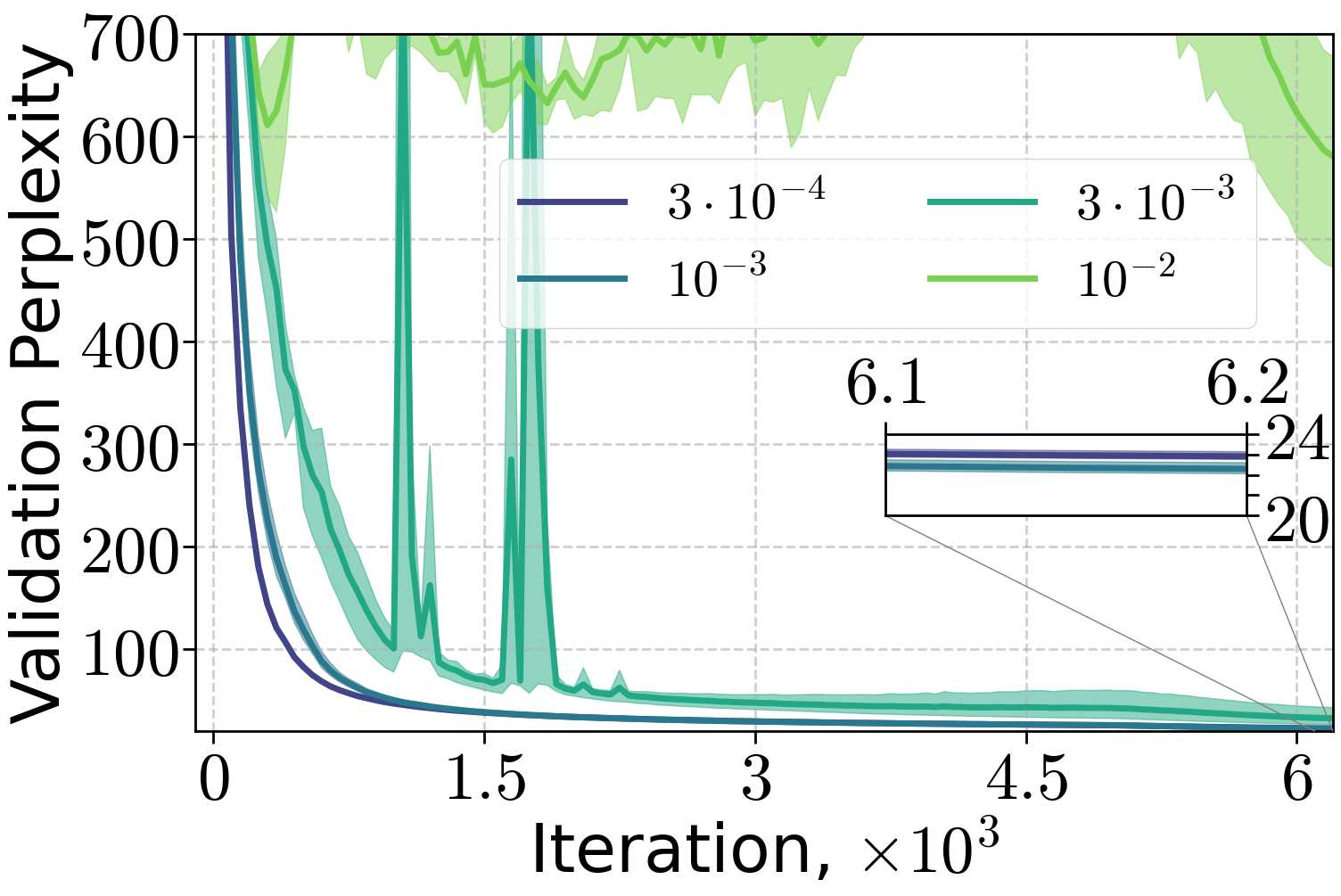
Figure 7: Training of 70M and 160M LLMs on FineWeb dataset, varying the peak learning rate with 10% linear warm-up and $(H_0, H_1)$ warm-up with $C=4$.

Limitations and Future Directions

The $(H_0, H_1)$-smoothness condition provides a tight curvature bound at the start of training, but the bound deteriorates after the warm-up phase, especially for LLMs. Future work should focus on identifying curvature bounds valid throughout the entire training trajectory and on extending the analysis to layer-wise smoothness, which may better capture the heterogeneous conditioning of deep networks. Further investigation is needed to establish $(H_0, H_1)$ warm-up as a practical replacement for linear warm-up in large-scale training pipelines.

Conclusion

This work establishes a principled theoretical foundation for learning rate warm-up in deep learning, introducing the $(H_0, H_1)$-smoothness condition and demonstrating its validity for common neural architectures and loss functions. The analysis shows that warm-up schedules derived from this condition yield provably faster convergence than fixed step-size strategies, with empirical results confirming the practical benefits for both language and vision models. The $(H_0, H_1)$ framework provides a robust basis for future research on optimization schedules and loss landscape analysis in deep learning.