Model-brain comparison using inter-animal transforms (2510.02523v1)

Abstract: Artificial neural network models have emerged as promising mechanistic models of the brain. However, there is little consensus on the correct method for comparing model activations to brain responses. Drawing on recent work in philosophy of neuroscience, we propose a comparison methodology based on the Inter-Animal Transform Class (IATC) - the strictest set of functions needed to accurately map neural responses between subjects in an animal population. Using the IATC, we can map bidirectionally between a candidate model's responses and brain data, assessing how well the model can masquerade as a typical subject using the same kinds of transforms needed to map across real subjects. We identify the IATC in three settings: a simulated population of neural network models, a population of mouse subjects, and a population of human subjects. We find that the IATC resolves detailed aspects of the neural mechanism, such as the non-linear activation function. Most importantly, we find that the IATC enables accurate predictions of neural activity while also achieving high specificity in mechanism identification, evidenced by its ability to separate response patterns from different brain areas while strongly aligning same-brain-area responses between subjects. In other words, the IATC is a proof-by-existence that there is no inherent tradeoff between the neural engineering goal of high model-brain predictivity and the neuroscientific goal of identifying mechanistically accurate brain models. Using IATC-guided transforms, we obtain new evidence in favor of topographical deep neural networks (TDANNs) as models of the visual system. Overall, the IATC enables principled model-brain comparisons, contextualizing previous findings about the predictive success of deep learning models of the brain, while improving upon previous approaches to model-brain comparison.

• The paper presents the novel IATC framework, enabling precise mapping between neural responses in models and biological brains.
• It introduces the Zippering Transform, which inverts non-linearity to achieve high predictivity and specificity across simulated and real neural data.
• Empirical analyses on mouse electrophysiology and human fMRI validate the bidirectional mapping approach for improved model separation and mechanistic insights.

Model-Brain Comparison Using Inter-Animal Transforms: A Technical Analysis

Introduction and Motivation

This paper introduces the Inter-Animal Transform Class (IATC) as a principled framework for comparing artificial neural network (ANN) models to biological brains. The IATC is defined as the strictest set of functions required to accurately map neural responses between subjects in a population for a given brain area. The central thesis is that model-brain comparisons should utilize the same empirical transforms needed to align brains to each other, thus enabling bidirectional mapping between models and brain data. This approach addresses the limitations of previous methods, such as linear regression and soft matching, which either lack specificity or predictive power, and provides a rigorous mechanism for evaluating mechanistic similarity.

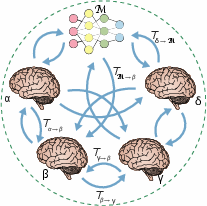
Figure 1: Schematic of model-brain comparison using the Inter-Animal Transform Class (IATC), illustrating bidirectional mapping between model and brain responses.

Formalization of the IATC

The IATC is formally defined as the strictest (smallest) set of functions that achieves maximal mapping accuracy across subjects. Strictness is operationalized as the minimality of the function set, ensuring that only necessary transforms are included. The estimation of the IATC involves optimizing both accuracy and strictness, typically constrained by known brain parcellations. The specificity metric, based on silhouette scores, quantifies the ability of a mapping to achieve within-area identifiability and between-area separability.

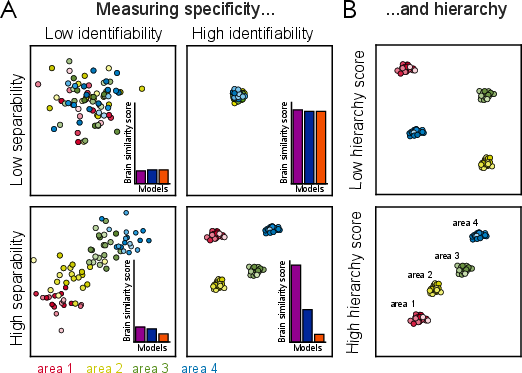
Figure 2: Evaluation of candidate transform classes for specificity and hierarchy, demonstrating the importance of within-area identifiability and between-area separability.

Empirical Identification of the IATC

Simulated Model Population

The authors first evaluate candidate transform classes on a simulated population of neural networks, specifically an AlexNet variant trained with contrastive learning and modified to use softplus activations with Poisson-like noise. The analysis reveals a "zippering" effect: pre-non-linearity activations are highly similar between subjects up to a linear transform, while post-non-linearity activations diverge due to the activation function, only to reconverge at the next layer's pre-activations.

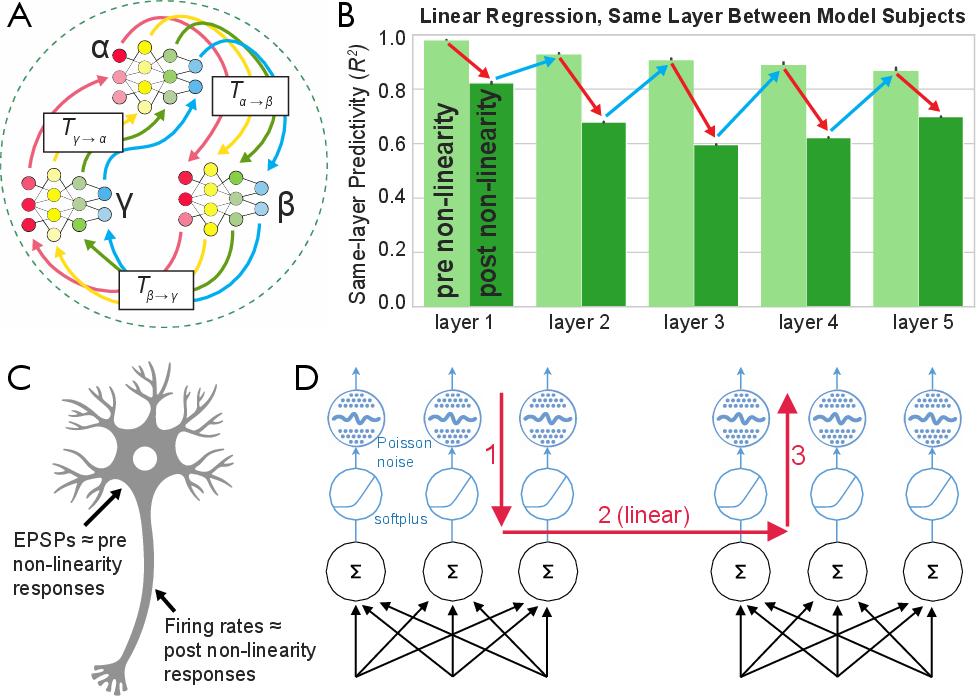
Figure 3: The zippering effect in model populations, showing divergence and reconvergence of activations across layers due to non-linearities.

To address this, the Zippering Transform is introduced, which inverts the non-linearity, applies a fitted linear transform, and reapplies the non-linearity. This approach yields near-ceiling predictivity and high specificity, outperforming both linear regression and soft matching.

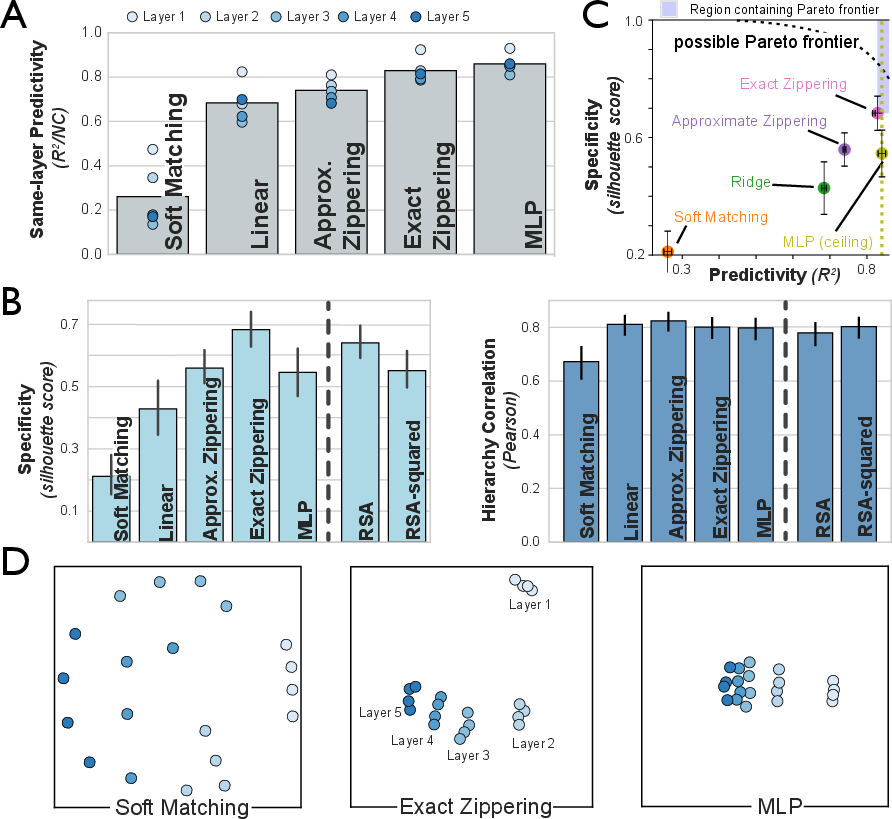
Figure 4: Predictivity and specificity for various transform classes in simulated model populations, highlighting the superiority of the Zippering Transform.

Mouse and Human Populations

The methodology is extended to real neural data: mouse electrophysiology and human fMRI. In mice, the Zippering Transform again improves predictivity and specificity over linear regression and soft matching, indicating that the activation function constrains the IATC in biological systems as well.

Figure 5: Assessment of transform classes on mouse populations, demonstrating improved predictivity and specificity with biologically motivated transforms.

In human fMRI data, ridge regression achieves the best intra-area cross-subject predictivity, with Zippering performing comparably. The lower resolution of fMRI likely obscures the effect of the activation function, but the rank order of transform classes remains consistent.

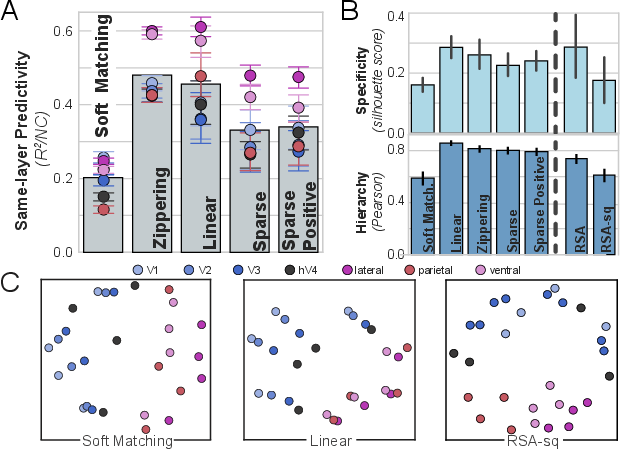
Figure 6: Evaluation of transform classes on human fMRI data, showing ridge regression as optimal for predictivity and specificity.

Bidirectional Mapping and Model Separation

A key innovation is the use of bidirectional mapping, aligning models to brains and vice versa. This approach enhances model separation, particularly in distinguishing topographical deep neural networks (TDANNs) from non-topographic models. Bidirectional ridge regression provides stronger evidence for the mechanistic similarity of TDANNs to the visual system than either unidirectional mapping or strict methods like soft matching.

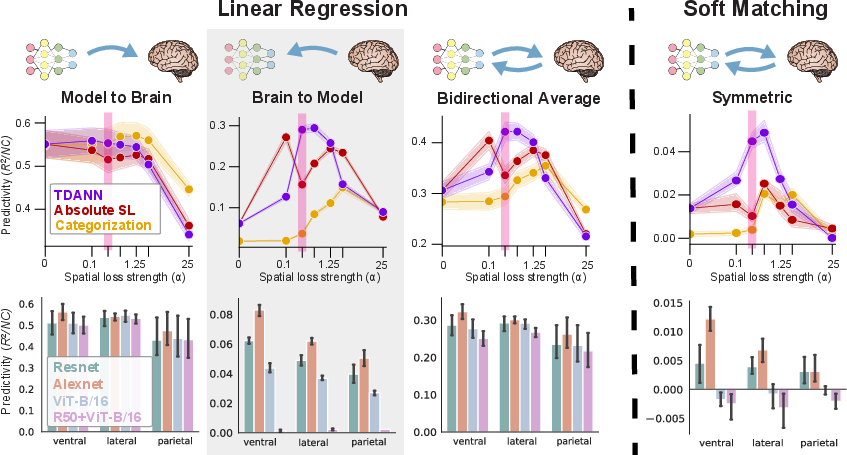
Figure 7: Bidirectional IATC-guided mapping improves separation between candidate models and human brain data.

Biological Consistency and Mechanistic Insights

The paper further motivates the use of softplus activations and Poisson-like noise in models by demonstrating their biological plausibility. Simulated spike counts fit softplus better than ReLU, especially in the sub-threshold regime, supporting the mechanistic relevance of the Zippering Transform.

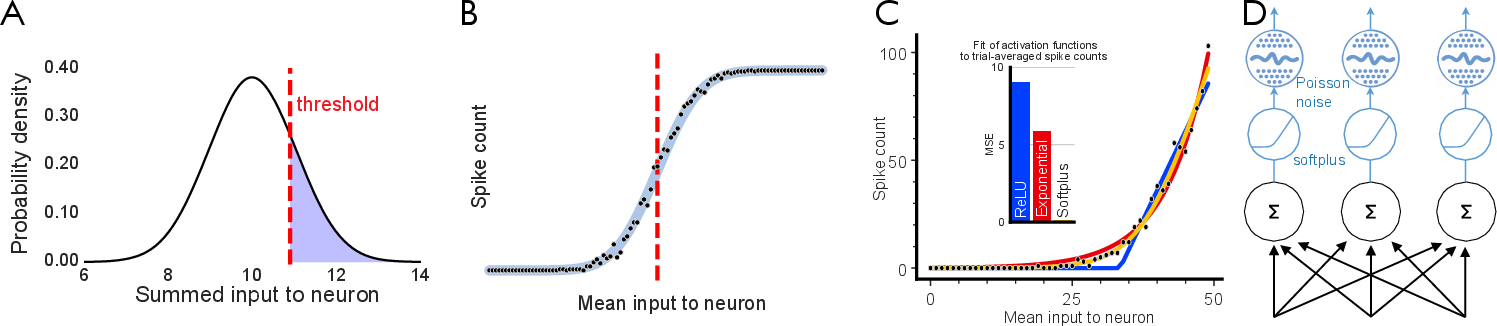
Figure 8: Biological activation functions modeled as noisy spiking processes, with softplus providing a superior fit to empirical spike counts.

Yeo-Johnson scaling is introduced as an approximate method for inverting unknown activation functions in real neural data, increasing the correlation between post-non-linearity and pre-non-linearity responses.

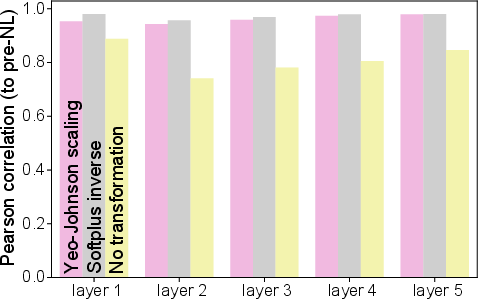
Figure 9: Correlation improvement between post- and pre-non-linearity responses after Yeo-Johnson scaling in noisy softplus models.

Implementation Details

Zippering Transform

The Zippering Transform is implemented as follows:

1. Invert Non-Linearity: Apply the inverse of the activation function (e.g., softplus) to the source responses.
2. Linear Mapping: Fit a linear transform (e.g., via GLM) between the inverted source and target pre-non-linearity responses.
3. Reapply Non-Linearity: Apply the activation function to the mapped responses to obtain post-non-linearity predictions.

import numpy as np from sklearn.linear_model import Ridge from scipy.special import softplus, expit def softplus_inv(y): return np.log(np.exp(y) - 1) def zippering_transform(X_source, Y_target, alpha=1.0): # Step 1: Invert softplus X_pre = softplus_inv(X_source) Y_pre = softplus_inv(Y_target) # Step 2: Fit linear mapping ridge = Ridge(alpha=alpha) ridge.fit(X_pre, Y_pre) Y_pre_pred = ridge.predict(X_pre) # Step 3: Reapply softplus Y_post_pred = softplus(Y_pre_pred) return Y_post_pred

Approximate Zippering

For unknown activation functions, Yeo-Johnson scaling is applied using sklearn's PowerTransformer:

from sklearn.preprocessing import PowerTransformer from sklearn.pipeline import Pipeline from sklearn.linear_model import Ridge pipeline = Pipeline([ ('yeo_johnson', PowerTransformer(method='yeo-johnson')), ('ridge', Ridge(alpha=1.0)) ]) pipeline.fit(X_source, Y_target) Y_pred = pipeline.predict(X_source)

GLM Implementation

GLMs are implemented using the glum package, specifying the inverse link function and Poisson noise structure. The weights are optimized via Iterative Reweighted Least Squares.

Trade-Offs and Performance Metrics

The paper demonstrates that the IATC approach resolves the perceived trade-off between predictivity and specificity. Strict methods (e.g., soft matching) fail to align same-area responses, reducing specificity, while overly flexible methods (e.g., deep MLPs) lose inter-area separation. The Zippering Transform achieves a Pareto-optimal balance, approaching the theoretical frontier for both metrics.

Performance metrics include:

• Predictivity: $R^2$ or noise-corrected Pearson correlation between predicted and actual responses.
• Specificity: Silhouette score quantifying within-area identifiability and between-area separability.
• Hierarchy Correlation: Pearson correlation between dissimilarity scores and known hierarchical distances.

Resource requirements scale with the number of subjects, neurons, and stimuli. For large-scale datasets, efficient implementations of GLMs and scalable optimization techniques are necessary.

Implications and Future Directions

The IATC framework provides a rigorous, mechanistically grounded method for model-brain comparison, enabling principled evaluation of ANN models as candidate brain models. The empirical identification of the IATC reveals that neural mechanisms, such as activation functions, shape the transform class required for accurate mapping. Bidirectional mapping enhances model separation and supports the identification of topographically organized models as more brain-like.

Future work should focus on:

• Data-Driven IATC Estimation: Leveraging large-scale optimization to learn the IATC directly from neural data, potentially refining brain parcellations and identifying cell-type-specific mappings.
• Hybrid Transform Classes: Incorporating privileged axes and subspace constraints to further improve strictness and flexibility.
• Statistical Methods for Source Noise Correction: Developing techniques to account for noise in both source and target populations, especially in brain-to-model mappings.

Conclusion

The Inter-Animal Transform Class (IATC) establishes a principled, empirically grounded methodology for comparing ANN models to biological brains. By optimizing both predictivity and specificity, and accounting for mechanistic details such as activation functions, the IATC approach advances the field of model-brain comparison. Bidirectional mapping and biologically consistent transforms enable more accurate identification of mechanistic models, with significant implications for both theoretical neuroscience and the development of brain-like artificial systems.