Transformers Discover Molecular Structure Without Graph Priors (2510.02259v1)
Abstract: Graph Neural Networks (GNNs) are the dominant architecture for molecular machine learning, particularly for molecular property prediction and machine learning interatomic potentials (MLIPs). GNNs perform message passing on predefined graphs often induced by a fixed radius cutoff or k-nearest neighbor scheme. While this design aligns with the locality present in many molecular tasks, a hard-coded graph can limit expressivity due to the fixed receptive field and slows down inference with sparse graph operations. In this work, we investigate whether pure, unmodified Transformers trained directly on Cartesian coordinates$\unicode{x2013}$without predefined graphs or physical priors$\unicode{x2013}$can approximate molecular energies and forces. As a starting point for our analysis, we demonstrate how to train a Transformer to competitive energy and force mean absolute errors under a matched training compute budget, relative to a state-of-the-art equivariant GNN on the OMol25 dataset. We discover that the Transformer learns physically consistent patterns$\unicode{x2013}$such as attention weights that decay inversely with interatomic distance$\unicode{x2013}$and flexibly adapts them across different molecular environments due to the absence of hard-coded biases. The use of a standard Transformer also unlocks predictable improvements with respect to scaling training resources, consistent with empirical scaling laws observed in other domains. Our results demonstrate that many favorable properties of GNNs can emerge adaptively in Transformers, challenging the necessity of hard-coded graph inductive biases and pointing toward standardized, scalable architectures for molecular modeling.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper asks a big question in chemistry and AI: Do we really need special “graph” models to understand molecules, or can a regular Transformer (the kind used in chatbots) learn chemistry just from where atoms are in space? The authors show that a plain Transformer, given only the 3D positions of atoms, can learn to predict important things like a molecule’s energy and the forces on its atoms—about as well as top graph-based models—and gets even better as it scales up.
What questions did the researchers ask?
They focused on a few simple, key questions:
- Can a standard Transformer (with no special chemistry tricks built in) match the accuracy of advanced graph neural networks (GNNs) for predicting molecular energies and forces?
- Does the Transformer learn sensible “physics-like” behavior on its own—like paying more attention to nearby atoms?
- Does its performance improve in a predictable way when you give it more data or make it bigger (called “scaling laws”)?
- Can this approach make training and running models faster using standard AI hardware?
How did they paper it?
To make their tests fair and clear, the researchers did the following:
- Transformers vs. GNNs (analogy):
- Think of a molecule as a group of people standing around. A GNN draws fixed “roads” between people who are close and lets messages flow along those roads. A Transformer doesn’t draw roads ahead of time. Instead, everyone can “pay attention” to everyone else and decide who matters most, depending on the situation.
- What the model sees:
- The Transformer gets the exact 3D positions of atoms (their x, y, z coordinates), plus other information like energy and forces during training.
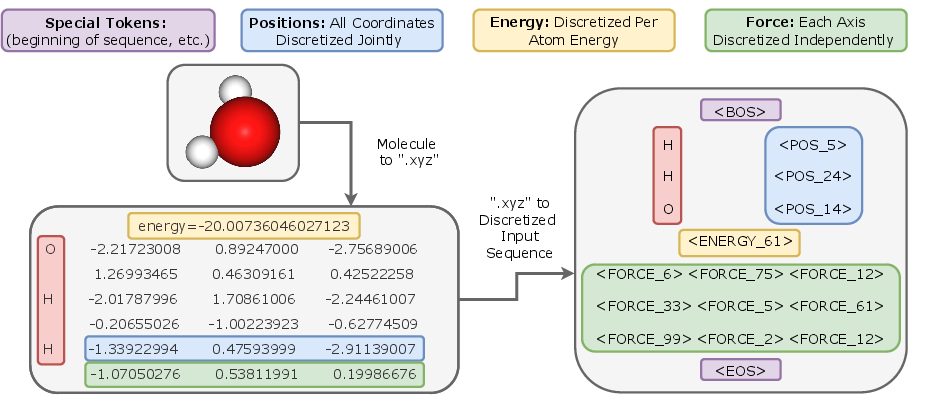
- To help learning, they provide both “tokens” (like labels in bins) and the true continuous numbers. This is like giving the model both a rounded number and the exact number.
- Training in two stages: 1) Pre-training: The model learns to predict the next pieces of the molecule’s information (like learning a language, but for atoms and their properties). This helps it understand general patterns. 2) Fine-tuning: The model switches to predicting the exact energy of the whole molecule and the force on each atom. This is the main goal for running simulations.
- Fair comparisons:
- They trained a big Transformer (about 1 billion parameters) and compared it to a strong GNN model on the same large dataset (OMol25) under a matching compute budget (so neither had an unfair advantage).
- They also checked how fast each model runs and how performance changes as the model size and training time scale up.
What did they find?
Here are the main results and why they matter:
- Accuracy and speed:
- The Transformer reached roughly the same accuracy as a top GNN for predicting molecular energies and forces.
- Even though the Transformer was much larger, it ran faster in practice. That’s because today’s hardware and software are heavily optimized for Transformers’ “dense” math, while GNNs use “sparse” graph operations that are harder to run quickly.
- Learned physics-like behavior (without being told):
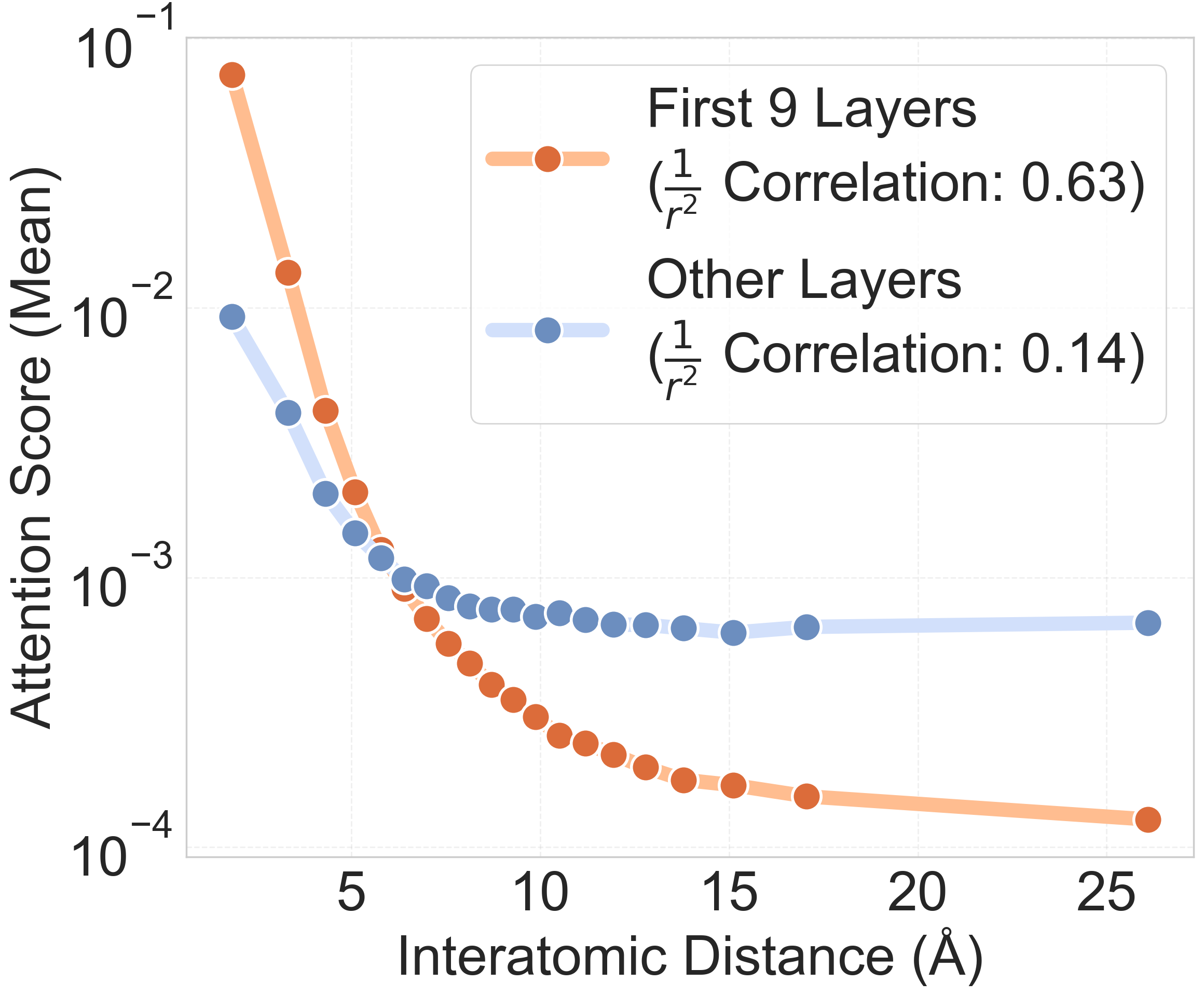
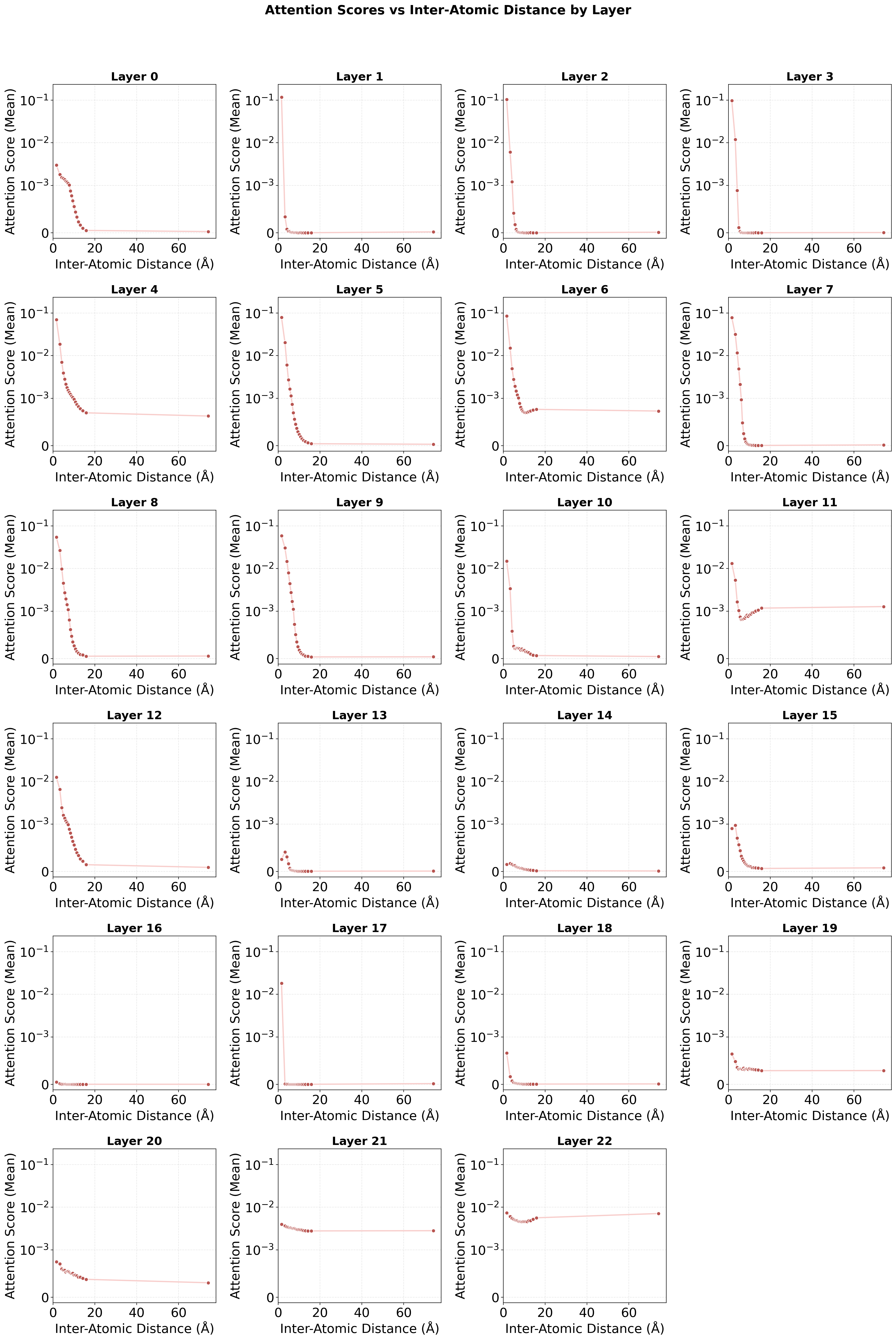
- The Transformer naturally learned to give more attention to nearby atoms and less to faraway ones—very similar to how many chemical interactions work.
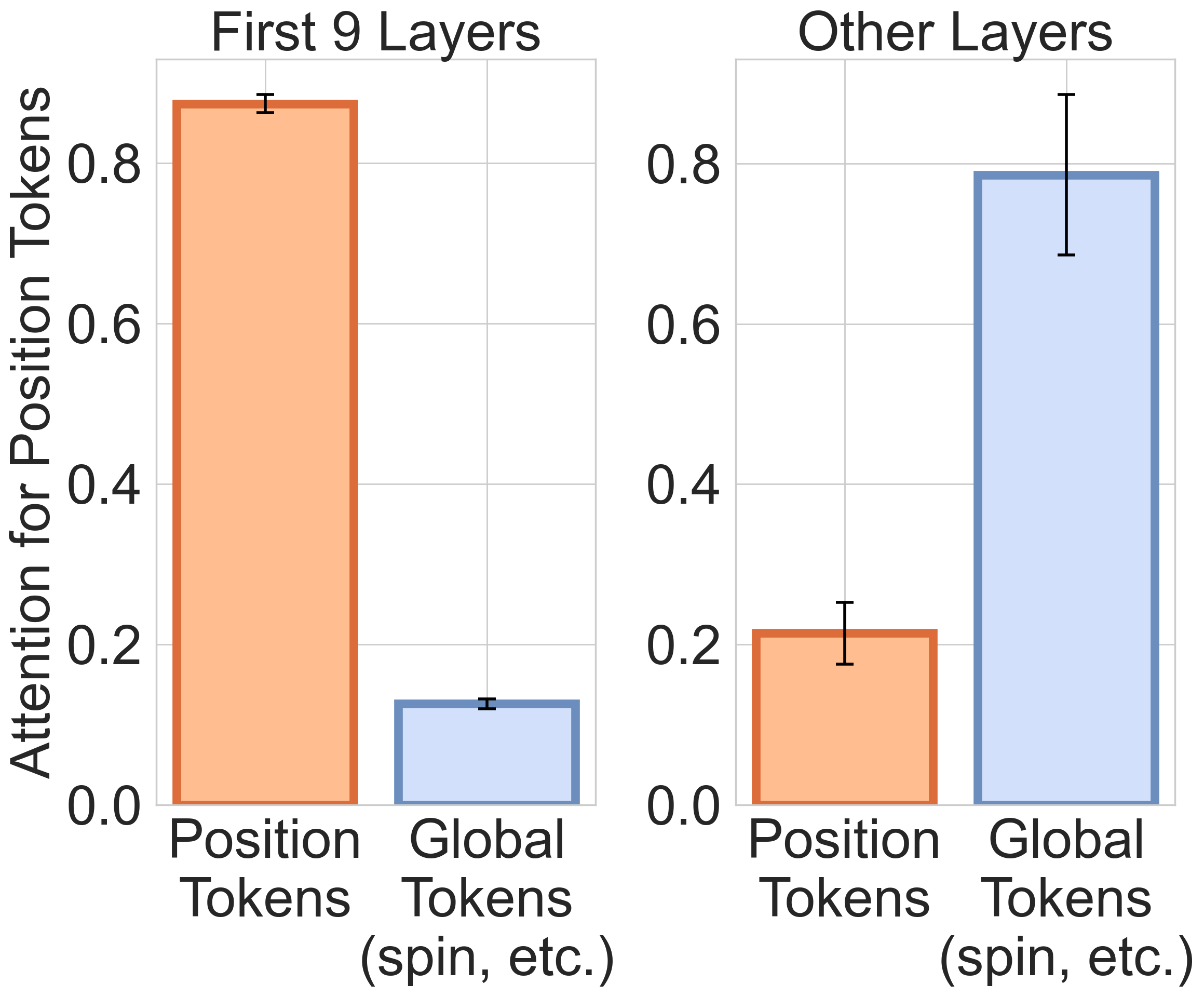
- Early layers of the model focused on local neighborhoods (nearby atoms), while later layers pulled together global information (like total charge or spin of the molecule). That’s like first looking at nearby details, then stepping back to see the whole picture.
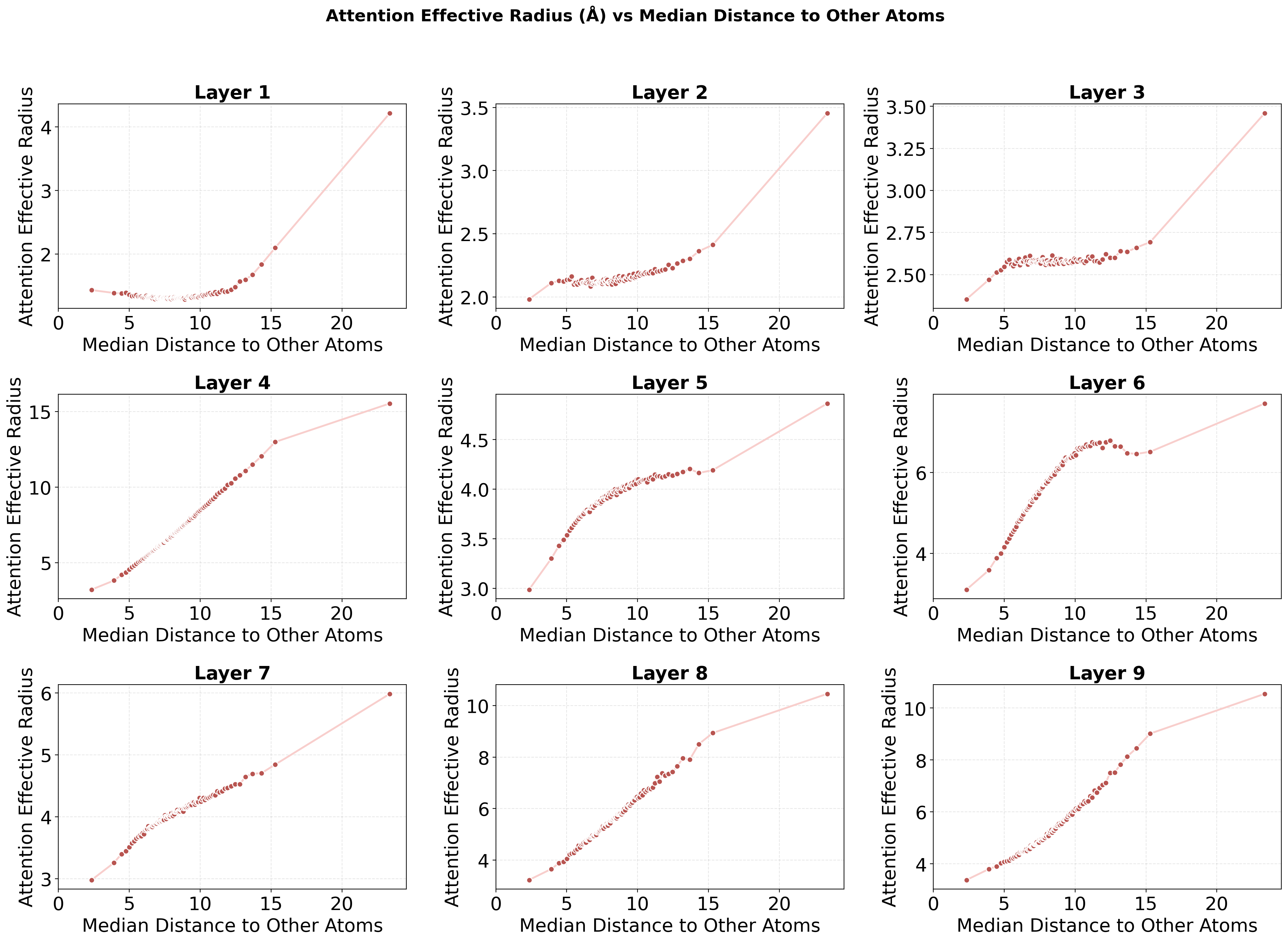
- The model adapted its “attention radius” based on how crowded an atom’s surroundings were: in dense regions, it focused locally; in sparse regions, it looked farther away. Graph models usually hard-code a fixed distance—this model learned to flex that distance by itself.
- Predictable scaling:
- As they increased model size and training, performance improved in a steady, predictable way, similar to known “scaling laws” in language and vision AI. This means we can plan for better results by planning more data or compute.
- Respecting symmetry:
- If you rotate a molecule, the physics shouldn’t change except for the directions of the forces. The model learned to behave almost like that just from data alone (high agreement when checking rotated versions), even without hard-coding rotational rules.
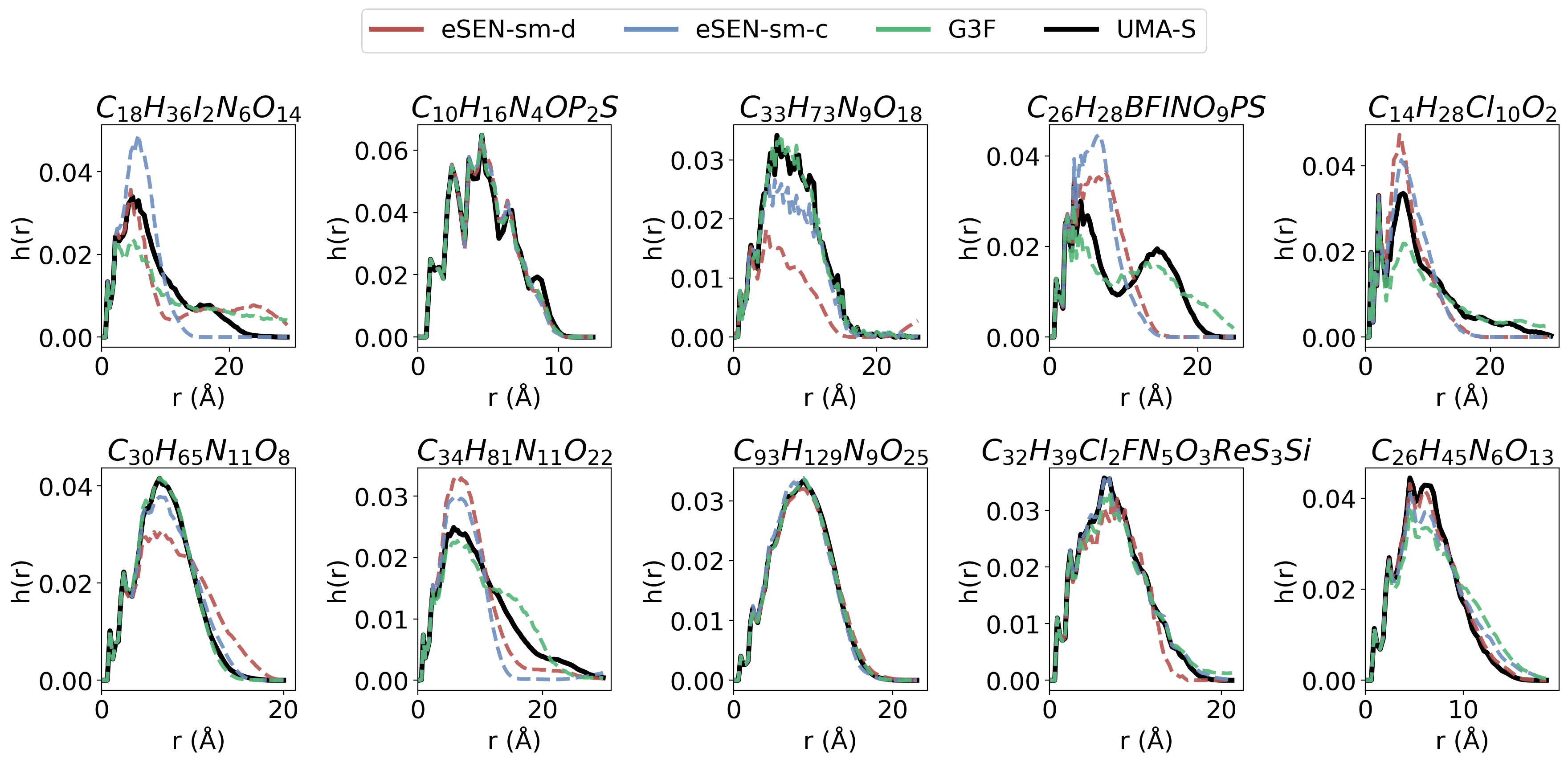
- Realistic simulations:
- The Transformer could run stable molecular dynamics simulations (like tiny atom movies) and estimate physical properties well.
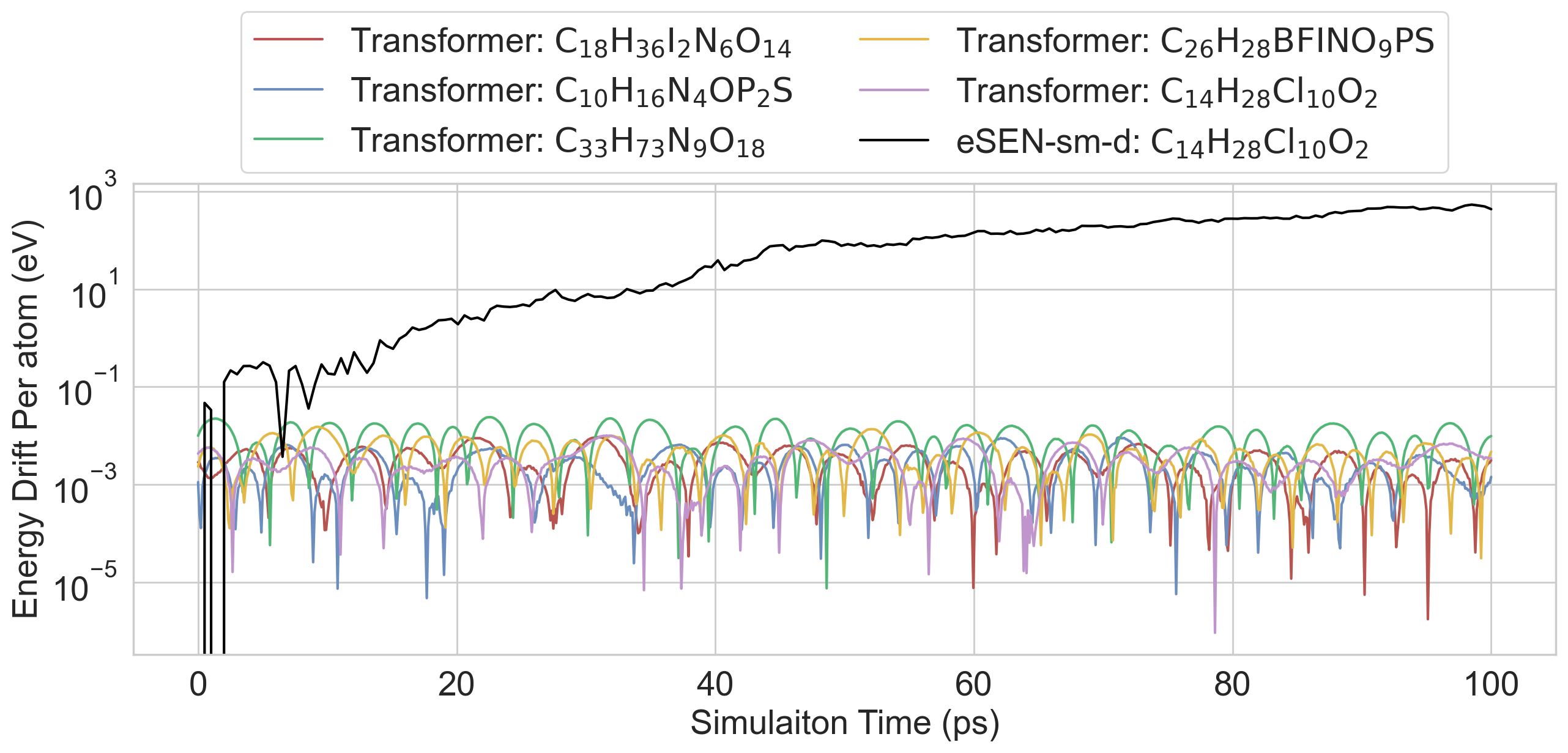
- With a small adjustment, it could also conserve energy in simulations that require it.
Why does this matter?
This work suggests a big shift for AI in chemistry:
- Fewer hand-crafted rules: Instead of designing complex graph structures and special physics features, a plain Transformer can learn many of these ideas from data. That makes models simpler to build and easier to scale.
- Faster and more scalable: Because Transformers fit well with modern hardware, we can train bigger and stronger models for chemistry, following clear scaling rules.
- More flexible: Since the model isn’t locked into a fixed graph, it can adapt to different molecules and environments. It can also be extended more easily to new inputs (like experimental signals) or used for different tasks (like generating new structures).
- Still cautious: The model doesn’t strictly enforce all physical laws by design. For safety-critical or highly precise scientific uses, researchers may want to add extra steps or constraints, or combine the Transformer with traditional physics-based models.
In short, this paper shows that a standard Transformer can “discover” meaningful molecular structure and physics-like behavior from data alone—matching expert graph models, scaling smoothly, and opening the door to more general, powerful, and practical tools for chemistry and materials science.
Knowledge Gaps
Knowledge Gaps, Limitations, and Open Questions
Below is a concise, actionable list of what remains missing, uncertain, or unexplored in the paper, intended to guide follow-up research.
- Sensitivity to atom ordering: the method uses sequences of atoms but does not rigorously test permutation invariance/equivariance to atom reordering; evaluate robustness under random permutations and design order-invariant tokenization or set-based encoders.
- Translation invariance: absolute Cartesian inputs without positional embeddings may still leak global position; explicitly test invariance to global translations and assess simple recentering/relative-coordinate preprocessing.
- Energy–force consistency: default training does not enforce F = −∇U; quantify non-conservative force components (e.g., via curl, path integrals), and benchmark penalties or architectures that enforce integrability at scale.
- Equivariance learned from data vs built-in: cossim > 0.99 suggests approximate rotational equivariance, but sample efficiency and generalization under unseen symmetry operations (e.g., reflections) are unquantified; add rigorous symmetry benchmarks and augmentation ablations.
- Long-range physics fidelity: attention decays with distance, but correctness of asymptotic behavior (e.g., Coulombic 1/r for charged systems) is not validated; test charged dimers at controlled separations and long-range interaction benchmarks.
- Periodic boundary conditions (PBC): extension to crystals/surfaces and minimum-image handling are unaddressed; evaluate on PBC datasets (e.g., OC20/OMat24), including long-range electrostatics (Ewald/PME) under PBC.
- Scaling with atom count: full attention is O(N2) in atoms; characterize runtime/memory vs system size and compare to sparse/local attention or learned neighbor pruning for systems with thousands of atoms.
- Cross-dataset and cross-domain generalization: results are limited to OMol25; test transfer to SPICE2, MD17/ANI, OC20/OMat24, Transition1x, and biomolecular benchmarks to validate breadth.
- Element and composition generalization: ability to extrapolate to unseen elements, oxidation states, and stoichiometries remains untested; design splits with unseen elements/charges to quantify.
- Geometry OOD robustness: performance under far-from-equilibrium geometries, bond-breaking/forming, and reactive pathways is not evaluated; add reaction coordinate scans and NEB-like tests.
- Data efficiency: Transformers typically require large data; quantify few-shot/low-data performance, and compare sample efficiency versus graph-based MLIPs.
- MD validation depth: provide long-horizon NVE/NVT results with standard diagnostics (energy drift, temperature/pressure stability, RDFs, VACFs, diffusion constants), failure rates, and robustness across systems and temperatures.
- Uncertainty quantification (UQ): discrete heads are proposed but not evaluated; implement calibrated UQ (e.g., ECE, coverage) and OOD detection for active learning and safe deployment.
- Pretraining objective design: only autoregressive token prediction is studied; compare against masked modeling, denoising, diffusion/score pretraining, and contrastive objectives for downstream accuracy and data efficiency.
- Input representation ablations: quantify the contribution of discretized tokens vs continuous channels, binning resolution, and alternative encodings (e.g., Fourier features, learned pairwise distances).
- Causality of attention patterns: inverse-distance behavior is descriptive; test necessity via attention head ablations, targeted masking, or pruning to show which heads/features drive accuracy.
- Energy extensivity and size generalization: verify linear scaling of total energy with system size and test tile-and-stitch or coarse-graining experiments to confirm extensivity assumptions from per-atom aggregation.
- Charge/spin conditioning: robustness to mis-specified global tokens and interpolation between charge/spin states is unknown; test sensitivity and add constraints ensuring charge conservation where applicable.
- Compute fairness and reproducibility: “matched FLOPs” across architectures can be misleading; replicate with multiple seeds/hardware, report error bars, and standardize FLOP accounting for fair comparisons.
- Learned vs imposed equivariance trade-offs: quantify when learned equivariance matches or lags explicit E(n)-equivariant models in low-data regimes and under symmetry stress tests.
- Context length limits: specify maximum atom/context length, behavior near/exceeding it, and strategies (chunking, pooling, recurrence) for larger molecules and condensed-phase systems.
- Electrostatics under PBC and in vacuum: evaluate whether the model learns dielectric-dependent behavior and field effects; incorporate physically-informed tests with external fields and varied dielectric environments.
- Multi-task loss balance: forces MAE lags the GNN; paper energy–force weighting schedules and report Pareto frontiers optimizing MD stability vs static accuracy.
- Interpretability beyond attention: add linear probes/diagnostics for learned chemical concepts (e.g., bond order, hybridization, local symmetry) and compare to classical descriptors.
- Failure modes and safety: test adversarial/edge cases (atom overlap, extreme bond lengths/angles), quantify numerical instabilities, and define guardrails for MD integration.
- Generative capability: pretraining claims joint modeling of positions/forces/energies, but no generation is shown; evaluate validity, uniqueness, stability, and property distributions for generated structures vs diffusion baselines.
- Multi-modal conditioning: conditioning on experimental modalities or DFT level is proposed but untested; prototype tasks (e.g., property-conditioned inference) and quantify gains.
- Atom identity embeddings: element embeddings ignore periodic table structure; test structured embeddings (e.g., learned periodic features) for extrapolation to heavier/rare elements.
- Augmentation coverage: only rotations are mentioned; test translation, reflection, and chirality-preserving augmentations, and quantify their impact on invariance and accuracy.
- Precision and stability: detail numerical choices (normalization, precision, clipping) for continuous inputs and assess their impact on stability and performance at scale.
- Carbon/compute footprint: scaling beyond 1B parameters is advocated, but training cost vs accuracy and environmental impact trade-offs are not analyzed; provide scaling-cost curves and efficiency strategies (MoE, distillation, sparsity).
Practical Applications
Immediate Applications
Below are specific, near-term uses that can be deployed with modest engineering, leveraging the paper’s graph-free Transformer that predicts molecular energies and forces competitively with state-of-the-art GNN MLIPs, and supports stable MD (NVT, NVE) while scaling efficiently on standard Transformer hardware.
- Accelerated molecular dynamics (MD) and property evaluation as a DFT surrogate
- Sectors: materials, chemicals, energy (batteries/electrolytes), pharmaceuticals (small molecules), semiconductors, automotive/aerospace (coatings, alloys)
- Tools/products/workflows: plug-in force field for ASE/LAMMPS/GROMACS; cloud/HPC inference services for batch property screening; workflow recipes that swap DFT calls for Transformer inference during MD or geometry optimization
- Assumptions/dependencies: accuracy validated on OMol25-like chemistries; conservative-force fine-tuning for NVE; careful OOD detection when moving to condensed-phase or periodic systems; rotational data augmentation or frame-averaging if stricter equivariance is needed
- High-throughput screening at scale on commodity Transformer stacks
- Sectors: materials discovery, drug-like molecule prioritization, catalysis pre-screening, polymer design
- Tools/products/workflows: GPU-optimized inference pipelines (TensorRT/FlashAttention/PyTorch 2), microservices that rank candidates by predicted stability/forces; “queue-and-score” services for thousands to millions of structures/day
- Assumptions/dependencies: coverage of target chemistry/domain by training data; batch sizing and mixed-precision tuned for latency/cost targets; clear acceptance criteria (MAE targets) against baseline DFT/GNN for intended use
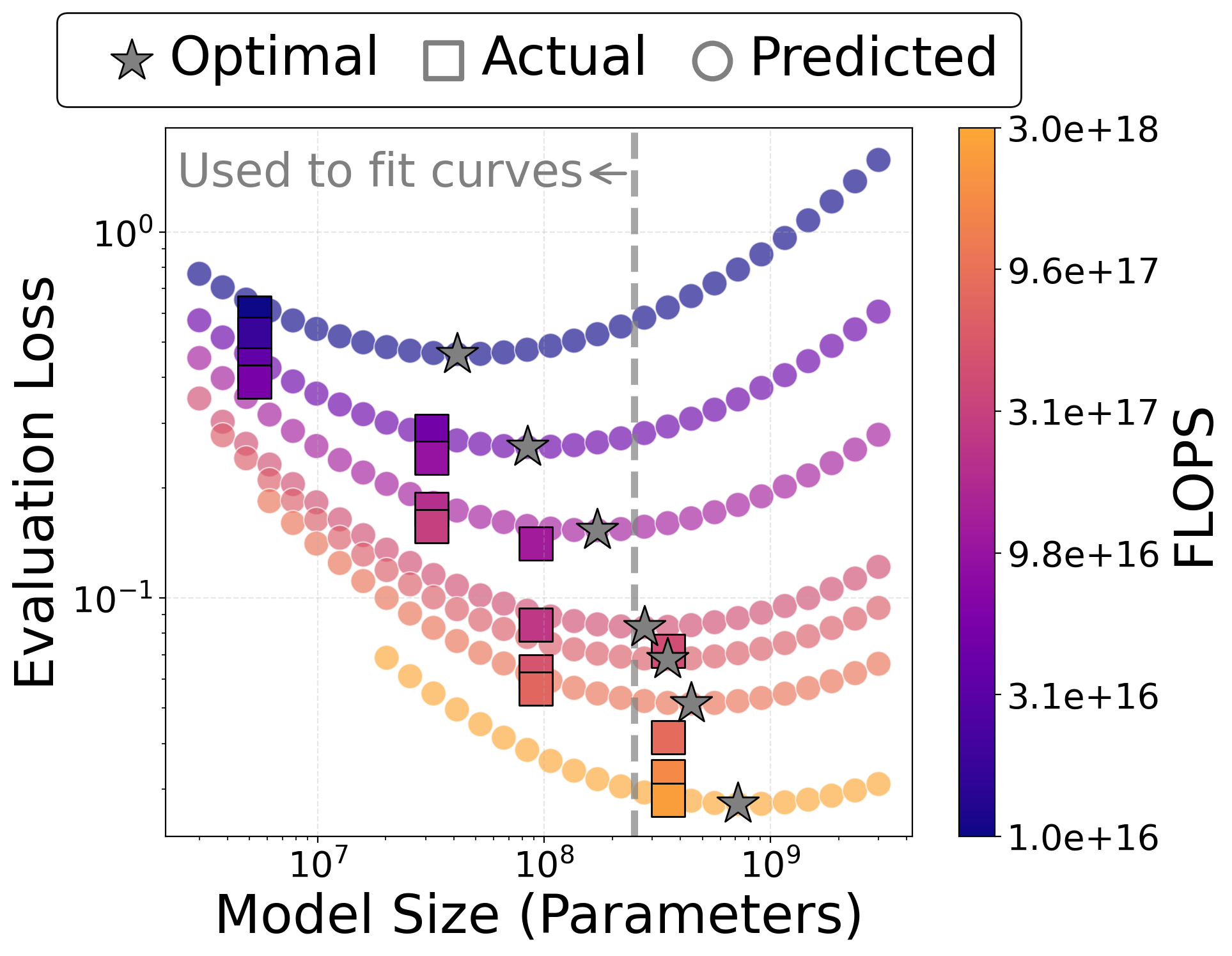
- Budget-aware model planning using scaling laws
- Sectors: software, cloud/HPC operations, finance/IT procurement within R&D orgs
- Tools/products/workflows: compute/performance planners using IsoFLOP curves to pick model size vs. epochs for a fixed budget; dashboards that forecast accuracy vs. dollars vs. wall-clock
- Assumptions/dependencies: scaling trends hold near chosen regime; data/optimizer settings similar to the paper’s recipes; tracking validation curves to detect deviations from predicted power laws
- Active learning loops with uncertainty signals and likelihoods
- Sectors: materials/chemistry R&D, platform AI for modeling
- Tools/products/workflows: pretrain head for likelihood estimation; acquisition strategies that pick points for DFT re-labeling; attention- and likelihood-based OOD monitors
- Assumptions/dependencies: calibrated uncertainty (may require post-hoc calibration or ensembles); query strategies tuned to lab throughput; guardrails for failure modes (e.g., radical species, unusual charge states)
- Distillation into smaller, physics-constrained MLIPs for production
- Sectors: embedded/edge simulation, real-time in-the-loop control, large MD campaigns
- Tools/products/workflows: knowledge distillation from the Transformer into MACE/eSEN-like models or hybrid conservative heads; teacher–student pipelines to retain accuracy at lower latency/cost
- Assumptions/dependencies: student capacity sufficient; consistency losses (e.g., forces/energies) and conservative constraints well-posed; careful selection of transfer set covering deployment regimes
- Attention analytics to guide feature engineering or cutoff selection in legacy GNNs
- Sectors: academic MLIP development, enterprise modeling platforms
- Tools/products/workflows: analysis kits that surface inverse-distance and adaptive receptive-field patterns; tools to tune graph cutoffs/radii by environment density
- Assumptions/dependencies: attention–physics interpretability holds across target chemistries; analytics used as decision support (not as proof of causality)
- Standardized Transformer baselines for benchmarks and reproducibility
- Sectors: academia, consortia/benchmark boards, open-source communities
- Tools/products/workflows: reference checkpoints trained on OMol25; cookie-cutter training configs; baseline leaderboards separate from graph-centric models
- Assumptions/dependencies: open licensing for datasets and model weights; transparent compute accounting; maintained repos and CI to prevent bit-rot
- Educational/skills development modules for “ML for chemistry” courses
- Sectors: education, upskilling within industry R&D
- Tools/products/workflows: interactive notebooks showing attention vs. distance; labs on pretrain–finetune, scaling-law fitting, and MD stability tests
- Assumptions/dependencies: curated teaching subsets of OMol25; modest GPU availability for class exercises; alignment with institutional compute policies
- Early-stage policy and governance pilots around MLIPs
- Sectors: government labs, standards bodies, R&D compliance
- Tools/products/workflows: internal checklists for MD stability, OOD stress tests, energy conservation verification; data-governance templates for training/validation splits and provenance
- Assumptions/dependencies: participation from domain experts; access to reference QM calculations for spot checks; agreement on acceptable error ranges per application
Long-Term Applications
These applications require additional research, scaling, or ecosystem development (e.g., broader datasets, rigorous validation under OOD, periodic boundary conditions, stricter physical constraints, or multi-modal integration).
- General-purpose atomistic “foundation models” for chemistry and materials
- Sectors: cross-sector (materials, pharma, energy, semiconductors, sustainability)
- Tools/products/workflows: billion- to hundred-billion-parameter models pre-trained across molecules, materials, surfaces, and periodic systems; adapters for task-specialization (phonons, elastic constants, reaction energetics)
- Assumptions/dependencies: large, diverse, high-quality datasets beyond OMol25 (periodic/condensed-phase, long-range electrostatics); scalable training pipelines; strong OOD monitoring; environmental/energy cost management
- Multi-modal, condition-aware simulation (linking computation and experiment)
- Sectors: advanced manufacturing, catalysis, battery R&D, pharmaceuticals
- Tools/products/workflows: models conditioned on DFT functional, temperature/pressure, solvent, spectra (IR/Raman/NMR), or microscopy; “data fusion” training that ties simulated and experimental domains
- Assumptions/dependencies: standardized schemas across modalities; robust domain-alignment strategies; careful treatment of experimental noise and biases
- Generative design of molecules/materials with property control
- Sectors: drug discovery, functional materials, polymers, electrolytes
- Tools/products/workflows: sequence-like generative heads to sample structures jointly with energies/forces; closed-loop optimizers that propose candidates and validate via fast MD; “design copilots” integrated into CAD-like environments
- Assumptions/dependencies: calibrated property predictors; safe exploration constraints; synthesis feasibility filters and retrosynthesis integration; IP and safety governance
- Autonomous laboratories and robotics for closed-loop discovery
- Sectors: robotics, materials/chemistry labs, process R&D
- Tools/products/workflows: planner–executor stacks where the model selects candidates, a robot synthesizes/tests, and data returns to retrain; scheduling systems that use uncertainty and scaling-law forecasts to balance exploration vs. exploitation
- Assumptions/dependencies: robust lab integration (LIMS/ELN), safety interlocks, standardized APIs; high reliability of the model in targeted chemical regimes; lifecycle MLOps for continuous learning
- Reliable MD for biophysics and binding energetics (e.g., free energy perturbation support)
- Sectors: healthcare/pharma
- Tools/products/workflows: long-timescale MD with accurate solvent and periodic boundary conditions; hybrid QM/MM emulation with ML surrogates; accelerated estimation of binding free energies or conformational populations
- Assumptions/dependencies: expanded training to include biomolecular systems, solvents, ions, PBCs; enforcement of conservative forces and constraints; validation against gold-standard experimental/benchmark sets
- Physics-informed and auditable MLIPs for safety-critical use
- Sectors: aerospace, nuclear, environmental safety, regulatory science
- Tools/products/workflows: models that provably enforce symmetries and energy conservation; formal verification tools; audit trails with interpretable attention heads and uncertainty records
- Assumptions/dependencies: hybrid training (energy-gradient heads, symmetry regularizers, frame averaging); standards for documentation and auditability; third-party certification ecosystems
- Property- and simulation-as-a-service platforms (“AtomGPT”)
- Sectors: software, cloud, enterprise R&D
- Tools/products/workflows: APIs for on-demand energies/forces/MD; managed active learning with on-call QM backends; usage-based billing and SLAs tuned by scaling-law forecasts
- Assumptions/dependencies: reliable multi-tenant isolation; cost controls; clear terms on data/IP; robust OOD refusal policies
- Cross-scale digital twins linking atomistics to continuum models
- Sectors: energy (batteries, electrolyzers), industrial process design, electronics
- Tools/products/workflows: pipelines that pass MLIP-derived parameters (diffusivities, reaction rates) into mesoscale/continuum simulators; in situ updating as conditions change
- Assumptions/dependencies: validated micro-to-macro parameter extraction; uncertainty propagation across scales; domain-specific calibration datasets
- Sustainability-aware compute strategies informed by scaling laws
- Sectors: policy, cloud/HPC providers, corporate sustainability
- Tools/products/workflows: procurement and scheduling policies that minimize carbon per unit of model accuracy; public reporting on accuracy–compute trade-offs
- Assumptions/dependencies: access to energy/carbon telemetry; accepted benchmarks to quantify “accuracy per watt-hour”; incentives for efficient training/inference
Notes on Cross-Cutting Assumptions and Dependencies
- Data coverage and quality: Success depends on diverse, high-fidelity datasets (including periodic/condensed-phase systems, long-range interactions, charged/solvated states), rigorous splits, and provenance tracking.
- Physical fidelity: For many deployments, enforcing conservative forces, approximate/effective equivariance, and stability under MD is essential; techniques include energy-gradient training, frame averaging, and physics-informed regularization.
- OOD generalization and safety: Attention/likelihood-based OOD detection and calibrated uncertainty are needed when extrapolating beyond OMol25-like regimes; establish escalation paths to QM recalculation.
- Compute and cost: While Transformers benefit from mature hardware/software, scaling to very large models requires careful cost, energy, and carbon budgeting; scaling laws help plan compute-efficient training.
- Integration: Production value hinges on robust integration with simulation engines (ASE/LAMMPS/GROMACS), lab systems (LIMS/ELN), and enterprise MLOps.
- Governance: Adoption in regulated or safety-critical contexts requires standards for validation, documentation, and auditability, as well as licensing clarity for data and models.
Taken together, the paper’s results support immediate deployment as a fast, general MLIP surrogate in screening and MD workflows, while opening a path toward multi-modal, foundation-scale, and autonomous design systems that could reshape how industry and academia conduct atomistic modeling.
Glossary
- Attention effective radius: The smallest distance around an atom that contains a specified fraction of its attention mass, used to characterize how far a token looks. "we define the effective attention radius as follows:"
- Attention scores: The numerical values produced by the attention mechanism indicating how strongly tokens attend to each other. "We focus on the learned attention scores---the softmax-normalized dot products between queries and keys---which reveal how the Transformer allocates attention across different layers."
- Autoregressive training: A training paradigm where the model predicts the next token given previous ones using a causal mask. "During the pre-training stage, we train the model autoregressively with a causal attention mask"
- Bi-directional attention mask: An attention configuration that allows tokens to attend to both past and future positions. "We replace the causal attention mask with a bi-directional one, making the model permutation equivariant."
- Cartesian coordinates: A representation of 3D positions using x, y, z values. "trained directly on Cartesian coordinates—without predefined graphs or physical priors—can approximate molecular energies and forces."
- Causal attention mask: An attention configuration that restricts tokens to attend only to previous positions to preserve autoregressive ordering. "train the model autoregressively with a causal attention mask"
- Conservative force field: A force field derived from a potential energy function where forces are negative gradients of energy. "conserve energy in NVE simulations when fine-tuned to predict a conservative force field: "
- Cross-entropy loss: A common objective function for classification measuring the difference between predicted distributions and true labels. "to predict all discrete tokens in the sequence using a cross‑entropy loss."
- Density Functional Theory (DFT): A quantum mechanical method used to compute electronic structure and derive energies and forces. "which are generated from reference computational chemistry methods (like Density Functional Theory)."
- Equivariant GNN: A graph neural network whose outputs transform predictably under symmetry operations (e.g., rotations). "a state-of-the-art equivariant GNN"
- Energy gradient: The derivative of energy with respect to positions; its negative gives conservative forces. "fine-tuned to predict forces as an energy gradient"
- FLOPs: Floating point operations; a measure of computational cost for training or inference. "FLOPs for eSEN are estimated using the FairChem repository; FLOPs for our Transformer are estimated via HuggingFace tooling."
- Force field: A model that predicts forces (and often energies) for molecular simulations. "a graph-free Transformer can already serve as a molecular force field"
- Frame averaging: A technique to improve equivariance by averaging predictions over multiple rotated frames. "This value can essentially arbitrarily increase through frame averaging"
- Geometric descriptors: Handcrafted features summarizing geometric relationships (e.g., distances, angles) used in molecular models. "custom featurization, such as geometric descriptors"
- Graph bottlenecks: Structural limitations in graph message passing that hinder information flow across distant nodes. "The permutation invariance and graph bottlenecks in message passing schemes can lead to oversmoothing"
- Graph inductive biases: Model design assumptions that encode graph-related priors, such as locality or neighbor definitions. "challenging the necessity of hard-coded graph inductive biases"
- Graph Neural Networks (GNNs): Neural architectures that operate on graph-structured data, passing messages along edges. "Graph Neural Networks (GNNs) are the dominant architecture for molecular machine learning"
- Heavy-tailed distributions: Distributions with large probability mass in the tails, often spanning multiple orders of magnitude. "Continuous molecular features such as positions, forces, and energies often exhibit heavy-tailed distributions spanning multiple orders of magnitude"
- IsoFLOP curves: Performance curves at constant compute budgets, trading off model size and training duration. "We plot predicted IsoFLOP curves, where smaller models on each curve are trained for more epochs and larger ones are trained for fewer epochs."
- k-nearest neighbor scheme: A graph construction method connecting each node to its k closest neighbors. "often induced by a fixed radius cutoff or -nearest neighbor scheme."
- k-nearest-neighbor behavior: An attention pattern where a head attends based on neighbor rank rather than pure distance. "we observe certain heads exhibit a nearest-neighbor behavior,"
- Level of theory: The specific methodological and basis-set choices in quantum chemistry calculations. "calculated at the B97M-V/def2-TZVPD level of theory."
- Likelihood estimation: Computing the probability of observed data under a learned generative model. "enabling likelihood estimation"
- Machine Learning Interatomic Potentials (MLIPs): ML models that approximate potential energy surfaces and forces for atomistic systems. "Machine learning interatomic potentials (MLIPs) are a popular application area for graph neural networks (GNNs)."
- Mean Absolute Error (MAE): An evaluation metric measuring the average absolute difference between predicted and true values. "Energy MAE (meV)"
- Message passing: The core GNN operation where node embeddings are updated via aggregating information from neighbors. "GNNs perform message passing on predefined graphs"
- Mixture-of-experts: A modeling technique that routes inputs to specialized submodels to improve scalability or performance. "required a sophisticated mixture-of-experts scheme to train their largest models."
- NVE simulations: Molecular dynamics at constant number of particles, volume, and energy (microcanonical ensemble). "it can conserve energy in NVE simulations"
- NVT simulations: Molecular dynamics at constant number of particles, volume, and temperature (canonical ensemble). "run stable NVT simulations which accurately estimate thermodynamic observables"
- OMol25: A large open molecular dataset with energies and forces for diverse chemistries. "on the new OMol25 dataset"
- Oversmoothing: A GNN failure mode where node representations become indistinguishable as depth increases. "oversmoothing"
- Oversquashing: A GNN limitation where long-range information gets compressed through narrow graph paths. "oversquashing"
- Permutation equivariant: A property where permuting input atoms leads to a corresponding permutation of outputs. "making the model permutation equivariant."
- Permutation invariance: A property where outputs are unchanged under permutations of input order. "The permutation invariance and graph bottlenecks in message passing schemes can lead to oversmoothing"
- Positional embeddings: Learned vectors added to tokens to encode position; removed here because positions are explicit inputs. "removal of positional embeddings"
- Quantile binning: Discretization that assigns values to bins with equal numbers of samples. "we discretize continuous features using quantile binning"
- Radius cutoff: A distance threshold used to define edges in molecular graphs. "a fixed radius cutoff"
- Readout head: The final network layer(s) that map embeddings to task-specific outputs. "We also replace the linear readout head that outputs a distribution over discrete tokens with two energy and force readout heads."
- Receptive field: The spatial extent over which a model integrates information; fixed in many graph designs. "fixed receptive field"
- Rotational equivariance: A symmetry where outputs rotate consistently with inputs under rotations. "like rotational equivariance"
- Rotational frames: Different coordinate frames related by rotations used to assess equivariance. "forces predicted in different rotational frames:"
- Rotation augmentation: Data augmentation by rotating inputs to improve robustness and learn symmetries. "We train models for 10 epochs with rotation augmentation"
- Scaling laws: Empirical relationships predicting performance as a function of compute, data, and model size. "consistent with empirical scaling laws observed in other domains."
- SMILES: A text encoding of molecular structures (Simplified Molecular Input Line Entry System). "textual molecular descriptors (e.g., SMILES)"
- Sparse operations: Computations on sparse data structures (like graphs) that can be less hardware-efficient than dense tensors. "sparse operations in GNNs complicate efficient training on modern hardware."
- Thermodynamic observables: Physical quantities (e.g., temperature, pressure) measured in simulations to characterize system behavior. "accurately estimate thermodynamic observables"
- XYZ (.xyz) format: A simple text file format for molecular structures listing atomic species and Cartesian coordinates. "We transform the standard ``.xyz'' molecular representation into a discretized input sequence for our model."
- ωB97M-V/def2-TZVPD: A specific DFT functional and basis set combination used to compute reference labels. "calculated at the B97M-V/def2-TZVPD level of theory."
Collections
Sign up for free to add this paper to one or more collections.