2000 character limit reached
Convergence and Divergence of Language Models under Different Random Seeds (2509.26643v1)
Published 30 Sep 2025 in cs.CL and cs.LG
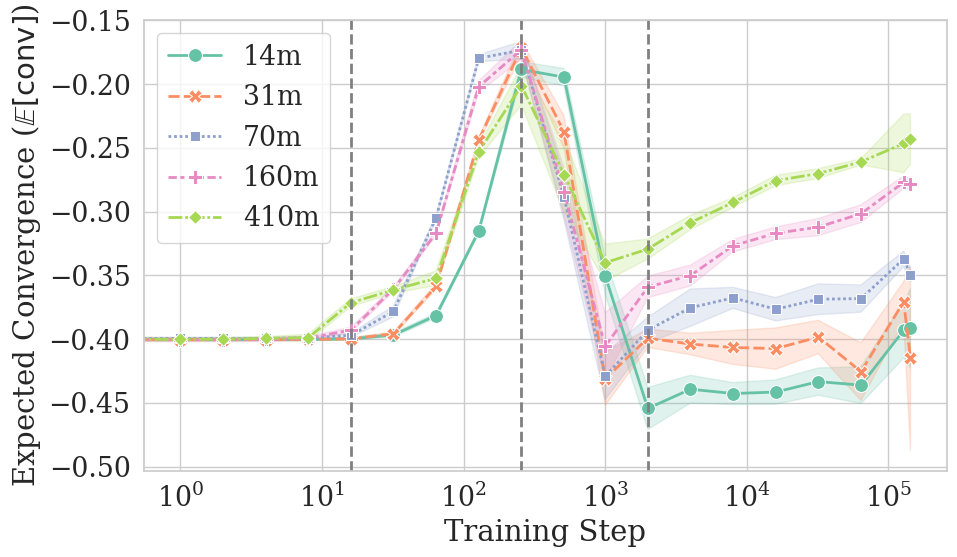
Abstract: In this paper, we investigate the convergence of LMs trained under different random seeds, measuring convergence as the expected per-token Kullback--Leibler (KL) divergence across seeds. By comparing LM convergence as a function of model size and training checkpoint, we identify a four-phase convergence pattern: (i) an initial uniform phase, (ii) a sharp-convergence phase, (iii) a sharp-divergence phase, and (iv) a slow-reconvergence phase. Further, we observe that larger models reconverge faster in later training stages, while smaller models never actually reconverge; these results suggest that a certain model size may be necessary to learn stable distributions. Restricting our analysis to specific token frequencies or part-of-speech (PoS) tags further reveals that convergence is uneven across linguistic categories: frequent tokens and function words converge faster and more reliably than their counterparts (infrequent tokens and content words). Overall, our findings highlight factors that influence the stability of the learned distributions in model training.
Summary
- The paper presents a novel analysis using expected per-token KL divergence to study language model convergence across random seeds.
- It identifies a four-phase training pattern that includes uniform, sharp-convergence, sharp-divergence, and slow-reconvergence phases using the PolyPythia suite.
- Results indicate non-uniform convergence across token frequency, PoS, and model size, highlighting challenges for reproducibility and model reliability.
Convergence and Divergence of LLMs under Different Random Seeds
Introduction
This paper presents a systematic investigation into the convergence properties of LMs trained under different random seeds, focusing on the expected per-token Kullback–Leibler (KL) divergence across seeds as a metric for convergence. The paper leverages the PolyPythia suite, which provides multiple independently trained models per size, enabling robust estimation of convergence dynamics. The analysis reveals a four-phase pattern in convergence during training and demonstrates that convergence is highly non-uniform across linguistic categories, token frequencies, and model sizes. These findings have significant implications for understanding the stability and reproducibility of LM training, as well as for the design of robust and reliable NLP systems.
Methodology
The authors define LM convergence as the negative expected KL divergence between the output distributions of two models trained with different random seeds. Formally, for a context , convergence is given by:
Expected convergence is then computed as the expectation of over contexts sampled from the data-generating distribution. Conditional convergence is introduced to analyze convergence restricted to tokens with specific properties (e.g., frequency, part-of-speech, surprisal).
Experiments are conducted on the PolyPythia models (sizes: 14M, 31M, 70M, 160M, 410M) at logarithmically spaced training steps, using a subset of the Pile validation set. Conditioning analyses are performed using token frequency, PoS tags (mapped from NLTK to subword tokens), and final surprisal.
Four Phases of Convergence
The empirical results reveal four distinct phases in the convergence dynamics of LMs:
- Uniform Phase: Early training (up to step 16) is characterized by models outputting near-uniform distributions, with minimal change in convergence across seeds. This is attributed to parameter initialization and low learning rates.
- Sharp-Convergence Phase: Between steps 16 and 256, models rapidly converge, shifting from uniform to unigram distributions. This phase aligns with the unigram-output stage previously identified in LM learning literature.
- Sharp-Divergence Phase: From steps 256 to 2k, models diverge as they begin to leverage context, resulting in decreased similarity across seeds. Notably, cross-entropy continues to decrease monotonically, indicating improved fit to the data-generating distribution despite increased divergence across seeds.
- Slow-Reconvergence Phase: After step 2k, models slowly reconverge, stabilizing predictions. Larger models reconverge more rapidly, while smaller models often fail to reconverge, suggesting a minimum model size is required for stable distribution learning. The onset of this phase coincides with induction-head formation and increased in-context learning scores.
Figure 1: Estimated convergence across training steps for different model sizes, illustrating the four-phase pattern and the relationship to cross-entropy and in-context learning.
These phases are also observed in downstream tasks (BLiMP) and in masked LLMs (MultiBERT), indicating the generality of the phenomenon.
Figure 2: Convergence dynamics on BLiMP and MultiBERT, showing similar phase transitions as in PolyPythia.
Conditional Convergence: Frequency, PoS, and Surprisal
Conditional analyses reveal substantial heterogeneity in convergence:
- Frequency: Frequent tokens exhibit rapid and stable convergence, while infrequent tokens are highly sensitive to random seed and often diverge throughout training. Final convergence for rare tokens is lower than at initialization.
- Part-of-Speech: Function words (e.g., determiners, pronouns, prepositions) converge more reliably than content words (nouns, verbs, adjectives). Content words remain volatile, with lower final convergence.
- Final Surprisal: Tokens with low final surprisal (high predictability) show strong convergence, whereas tokens with higher surprisal do not exhibit significant differences in convergence.
Figure 3: Conditional convergence for token frequency, PoS, and final surprisal, highlighting the uneven stability across linguistic categories.
Variance in convergence across contexts increases substantially during the sharp-divergence and slow-reconvergence phases, further emphasizing the non-uniformity of LM training dynamics.
Figure 4: Standard deviation of convergence across contexts, showing increased variance in later training phases.
Regression Analysis and Token-Level Insights
A linear regression analysis quantifies the impact of frequency, PoS, and model size on convergence. Frequency emerges as the dominant factor, with frequent tokens stabilizing earlier. Model size also plays a significant role, with larger models achieving higher convergence.
Figure 5: Regression coefficients for frequency and model size, demonstrating their influence on convergence.
Token-level KL divergence analysis identifies tokens with high, medium, and low divergence, providing granular insight into which tokens are most sensitive to random seed variation.
Practical and Theoretical Implications
The findings have several important implications:
- Reproducibility: LM training under different seeds can yield substantially different models, especially for rare tokens and content words. This challenges the assumption of model stability and has consequences for downstream applications requiring reproducibility.
- Model Size: Larger models are more likely to reconverge and learn stable distributions, suggesting a lower bound on model capacity for reliable training.
- Linguistic Structure: The uneven convergence across linguistic categories implies that certain aspects of language (e.g., function words) are more robustly learned, while others (e.g., content words) remain sensitive to initialization and optimization noise.
- Evaluation Metrics: Global metrics such as cross-entropy can mask significant variation in model behavior, underscoring the need for more granular evaluation methods.
- Future Directions: Extending convergence analysis to multilingual settings, alternative tokenization schemes, and other model families is necessary to generalize these findings. Addressing limitations in KL computation across different tokenizers and expanding the dataset scope are promising avenues.
Conclusion
This paper demonstrates that LLM convergence is a complex, multi-phase process, highly sensitive to model size, token frequency, and linguistic category. While global performance metrics improve monotonically, underlying convergence dynamics are non-uniform and context-dependent. These insights are critical for the development of robust, reproducible, and interpretable LLMs, and motivate further research into the mechanisms governing LM training stability.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper studies whether LLMs (computer programs that predict text) end up making the same kinds of predictions when they’re trained with different “random seeds” (different tiny starting choices). The authors measure how similar the models’ word-by-word predictions are as training goes on, and they discover a clear, four-stage pattern of becoming more similar and then less similar.
What questions are the researchers asking?
They focus on simple, practical questions:
- If you train the same model multiple times with different random seeds, do the models’ predictions become the same?
- How does this change over time during training?
- Does model size (small vs. large) matter?
- Do some kinds of words (like common words or function words) become more similar across models than others?
- Do these patterns also show up in other models and tasks?
How did they paper it? (With everyday analogies)
Think of several weather apps that all use the same method but start with different random numbers. Every day, you compare the apps to see if they give similar chances of rain. If their predictions match closely, they “converge.” If they differ a lot, they “diverge.”
Here’s what the team did, in plain terms:
- They trained several copies of the same LLM (“the same weather app”) but with different random seeds (“different starting coin flips”).
- They checked the models at many points during training (“snapshots” or “checkpoints”) to see how similar their predictions were for the next piece of text (a “token,” which is usually a word or part of a word).
- To measure similarity, they used a common score called KL divergence. You can think of KL divergence as a “difference score” between two probability predictions. A low KL means the models agree; a high KL means they disagree. They report convergence as the negative of that difference, so higher numbers mean “more similar.”
- They also looked at “conditional convergence,” which means checking similarity for specific kinds of tokens:
- By how frequent the token is (common vs. rare)
- By its part of speech (function words like “the” vs. content words like “cat” or “run”)
- By how predictable the token is at the end of training (low surprisal = easy to predict)
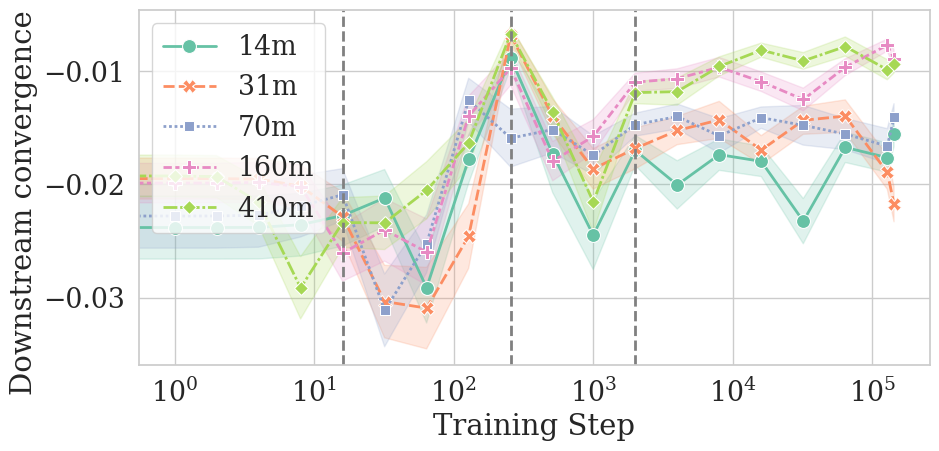
- They tested different model sizes and also looked for similar patterns in a downstream grammar task (BLiMP) and in a different kind of model (MultiBERT, which uses masked language modeling).
What did they find, and why does it matter?
They discovered four phases that happen during training. Here’s the simple version:
- Uniform phase (very early): Models act almost like they’re guessing evenly among all words (a “uniform” distribution). There isn’t much change in similarity yet.
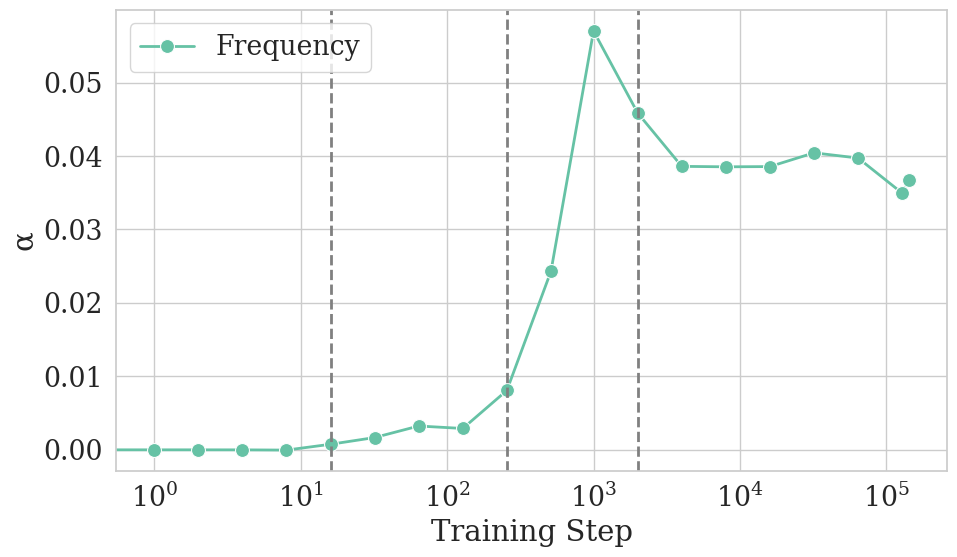
- Sharp-convergence phase: Models quickly become much more similar to each other because they learn basic word frequencies (for example, “the” appears more than “aardvark”). This matches earlier research showing that models first learn what words are common before they learn to use context.
- Sharp-divergence phase: Models start using context (the surrounding words), but they use it differently depending on their random seed. So they become less similar to each other for a while, even though they’re still getting better at the task overall.
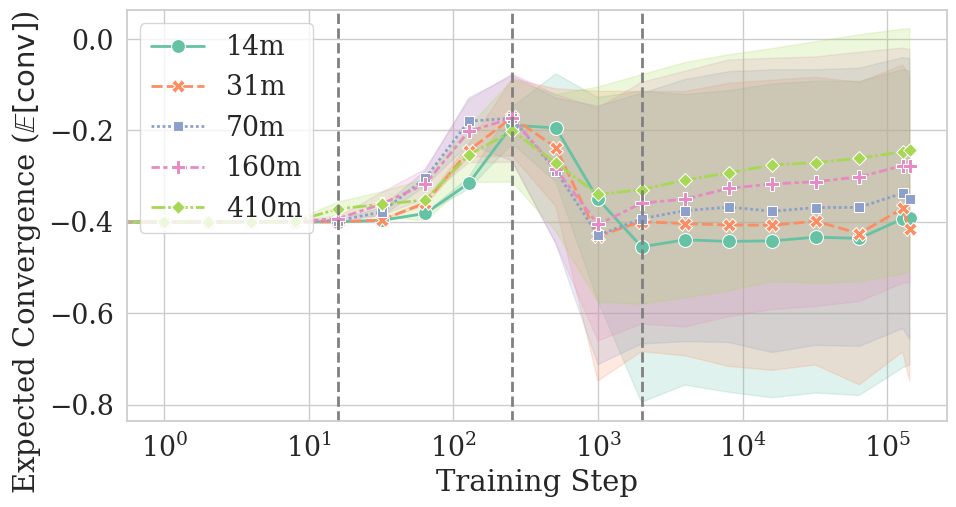
- Slow-reconvergence phase: Later on, models slowly become more similar again as their predictions stabilize. Larger models reconverge more strongly and more quickly; smaller models may never fully reconverge.
Why this matters:
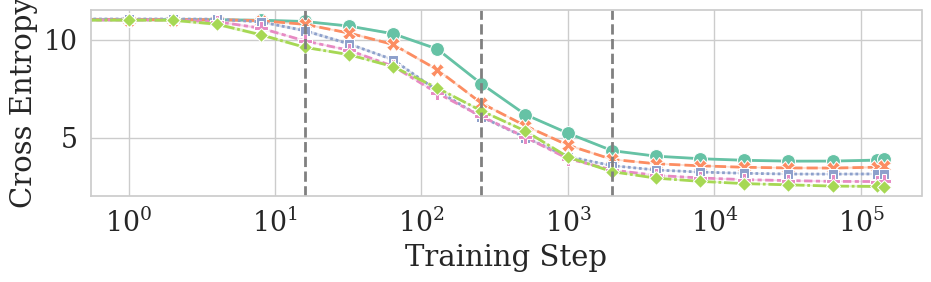
- Even when overall performance (like cross-entropy, a measure of “how surprised the model is”) keeps improving, models trained with different seeds can temporarily become less similar to each other. So “better” doesn’t always mean “more consistent across runs.”
- Bigger models tend to settle on similar solutions, which means they may be more reliable across reruns.
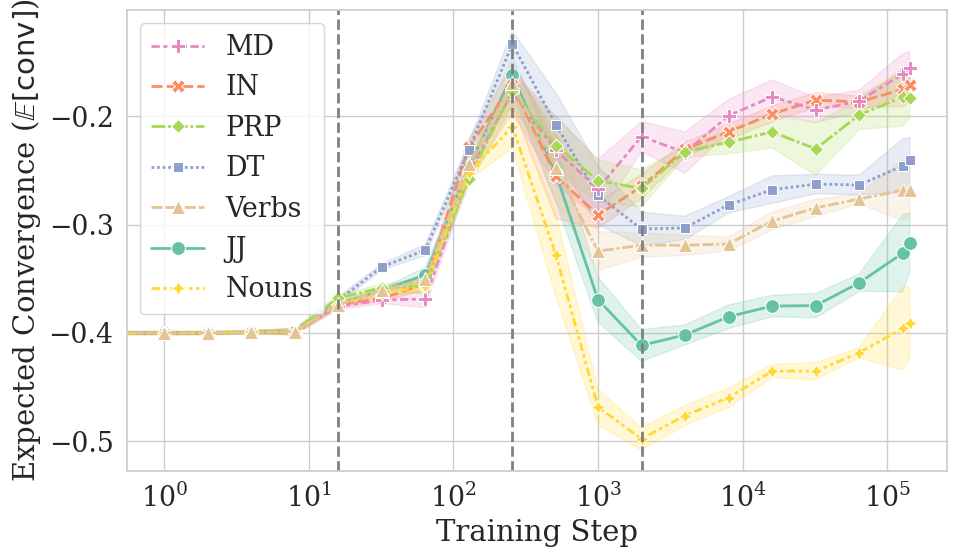
- Convergence is uneven across types of tokens:
- Frequent tokens and function words (like “the,” “of,” “and”) converge faster and more reliably.
- Rare tokens and content words (nouns, verbs, adjectives) are more variable and can end up less similar across models.
- The same general pattern appears in other tasks and in other model families, suggesting it’s a broader training behavior.
What’s the bigger picture?
This research helps us understand training stability and reliability:
- If you need consistent predictions across multiple training runs (for fairness, auditing, or scientific reproducibility), you should care about random seeds and model size. Larger models may be safer bets for stable behavior.
- Evaluations should consider not just “how good is the model?” but also “how consistent is it across different runs?” This is especially important for rare or content-heavy words, which can remain less stable.
- Training methods that stabilize how models use context (for example, techniques that help the “induction heads,” which enable in-context learning) may also improve consistency.
- For developers and researchers, relying on a single training run might hide instability, especially for rare or complex language. Checking across seeds gives a more honest picture.
In short: LLMs don’t steadily march toward being the same—they first become similar, then different, then slowly similar again. Bigger models settle down better, and simple, common words are learned in a more consistent way than rare, content-rich words. This insight can guide better training, evaluation, and deployment of LLMs.
Knowledge Gaps
Unresolved Knowledge Gaps and Open Questions
Below is a single, actionable list of knowledge gaps, limitations, and open questions that remain unresolved by the paper. Each point is phrased to guide follow-up research.
- Quantify the critical model size for “stable distributions.” The paper suggests a size threshold beyond which reconvergence occurs but does not estimate where this threshold lies or how it scales with parameters, depth, or heads.
- Formalize phase boundaries. The four phases (uniform, sharp-convergence, sharp-divergence, slow-reconvergence) are identified qualitatively and at rough step counts; a principled, reproducible criterion (e.g., change-point detection on a chosen metric) is missing.
- Causal link to induction-head formation. Reconvergence coincides with measured ICL improvements, but the paper does not test whether induction heads cause reconvergence (e.g., via targeted head ablations/interventions or causal circuit analysis).
- Isolate sources of randomness. “Seed” aggregates multiple randomness sources (weight initialization, data order/shuffling, dropout, augmentation, micro-batching); the contribution of each to divergence/reconvergence is not disentangled.
- Robustness to optimization and training schedules. The observed phases may be confounded by learning-rate warm-up and schedule choices; experiments varying LR schedule, optimizer, weight decay, gradient clipping, and curriculum are needed.
- Generalization across architectures and regimes. Beyond small autoregressive transformers (Pythia) and one masked LM suite (MultiBERT), the paper does not test MoE, LSTM/Mamba-like architectures, instruction-tuned/RLHF models, or billion-scale LMs.
- Tokenizer dependence and cross-family comparability. The KL-based metric assumes shared token supports; convergence across different tokenizers/model families is unexplored. Byte- or word-level remapping (as suggested) remains untested.
- Language and script coverage. Results are limited to English; whether the four phases and category-specific convergence (function vs content words) hold in morphologically rich languages or multilingual pretraining is unknown.
- Data-domain coverage. Analyses use 4,662 tokens from the Pile validation set; convergence dynamics across domains (code, dialogue, scientific text, long-form documents) and under domain shifts are not assessed.
- Rare-token divergence mechanisms. The finding that rare tokens diverge lacks a mechanistic explanation (data scarcity, tokenization fragmentation, context sensitivity, optimizer noise); targeted interventions (reweighting, data augmentation, smoothing) are not evaluated.
- Alternative divergence metrics. The paper focuses on negative expected KL; the sensitivity of phase detection to metric choice (e.g., JS divergence, total variation, Wasserstein distances, calibration error) is unstudied.
- Output-level vs representation-level convergence. Only output distributions are compared; representation geometry (layer-wise activations, effective rank, subspace alignment) and its relation to output convergence are not analyzed.
- Confidence interval methodology and estimator variance. The paper reports “1σ” intervals but does not specify the estimator variance decomposition (across contexts vs seed pairs), bootstrapping procedure, or independence assumptions among pairwise comparisons.
- Pairwise KL vs population structure. Using pairwise KL may miss structure across many seeds (e.g., clustering into distinct solution modes); population-level analyses (variance, clustering, mutual information) are not explored.
- Frequency and PoS confounds. Although a linear regression is provided, stronger multivariate controls (regularized or mixed-effects models) and causal tests are needed to disentangle correlated properties (e.g., function words also being frequent).
- PoS tagging reliability at subword level. The word-to-subword PoS mapping introduces potential noise and selection effects (tokens without majority labels are excluded); quantifying mapping error and testing alternative taggers/tokenization strategies is needed.
- Conditioning on “final surprisal” may be seed-dependent. Surprisal bins are derived from a single final checkpoint for a given size, potentially biasing analyses; robustness across seeds and conditioning on surprisal computed at multiple steps is not checked.
- Early-phase masked LM dynamics. MultiBERT lacks early checkpoints; whether masked LMs exhibit the initial uniform/sharp-convergence phases is unknown and requires training or acquiring early checkpoints for masked models.
- Task-level generalization beyond BLiMP. Downstream convergence is only tested on grammaticality judgments with a restricted support; convergence dynamics across diverse tasks (QA, summarization, code generation, retrieval, long-context reasoning) remain open.
- Context-length sensitivity of ICL proxy. The ICL measure compares surprisal at the 500th token under 50 vs 400 tokens of context; the dependence on position, context length, and content is not systematically varied.
- Tail behavior and numerical stability in KL. KL can be dominated by low-probability mass; the impact of numerical precision, logits clipping, or softmax temperature on measured divergence (especially for rare tokens) is not assessed.
- Dataset weighting and sampling biases. Expected convergence averages over observed contexts; the effect of frequency-weighted sampling vs stratified/balanced sampling on estimated phases and conditional convergence is untested.
- Cross-entropy vs seed divergence paradox. Models get closer to p_true while seeds diverge; a theoretical account (e.g., multiple near-optimal basins, path multiplicity) and links to loss landscape geometry (Hessian, flatness) are not developed.
- Scaling laws for convergence speed. Larger models reconverge faster, but no functional relationship (e.g., power-law exponents) is fitted; quantifying convergence speed as a function of parameters, depth, and attention heads is an open direction.
- Impact of regularization. The role of dropout, label smoothing, stochastic depth, and other regularizers on convergence/divergence phases is not studied.
- Effect of training data randomness vs fixed data order. If data order differs across seeds, it can drive divergence; experiments with fixed-order training to isolate initialization-only effects are needed.
- Phase detection under different datasets and optimizers. Whether the four-phase pattern is universal or dataset/optimizer-specific is unresolved; replicate with alternative corpora and optimizers (AdamW vs Adafactor vs SGD variants).
- Practical mitigation strategies. No strategies are tested to reduce across-seed divergence on unstable categories (e.g., rare/content words), such as targeted pretraining, curriculum learning, or loss reweighting.
Practical Applications
Immediate Applications
The following applications can be deployed now by leveraging the paper’s findings, metrics, and workflows.
- Sector: software/ML engineering (MLOps)
- Use case: training stability monitoring via expected per-token KL across seeds
- Description: integrate the paper’s convergence metric (expected KL between model outputs trained under different seeds) to detect the four-phase pattern and identify sharp-divergence windows (≈ steps 256–2k) where models start using context and seed variance spikes.
- Tools/workflows: add convergence dashboards alongside cross-entropy; alerting during divergence; checkpoint tagging; CI gates for stability thresholds.
- Assumptions/dependencies: multiple seeds of the same architecture and tokenizer; access to intermediate checkpoints; compute overhead for multi-seed training.
- Sector: software/ML engineering (model selection and QA)
- Use case: seed-stability benchmarking
- Description: benchmark candidate models by measuring cross-seed KL at key checkpoints; prefer larger models when stability is required, as they reconverge faster and more reliably.
- Tools/workflows: “seed-stability score” integrated into model cards; automated unit tests measuring stability on held-out data (e.g., subset of The Pile, BLiMP pairs).
- Assumptions/dependencies: shared tokenizer; English-centric datasets; stability may vary by domain.
- Sector: safety-critical industries (healthcare, finance, legal)
- Use case: ensemble averaging across seeds for reliable outputs
- Description: deploy inference-time ensembles by averaging probabilities across models trained with different seeds to reduce variance, especially for high-surprisal tokens and content words.
- Tools/workflows: seed-ensemble LM service; probability averaging or logit ensembling; distillation of ensemble into a single “stable student” model.
- Assumptions/dependencies: additional inference cost; model homogeneity; governance approval for ensembling.
- Sector: software/product (consumer AI writing assistants)
- Use case: reliability-aware decoding
- Description: adapt decoding strategies based on token class: lower temperature or stricter sampling for content words/rare tokens (high seed variance) and more permissive decoding for function words/frequent tokens (stable).
- Tools/workflows: dynamic temperature/top-p by PoS or token frequency; fail-safe prompts for predictable tokens when consistency is critical (e.g., email subject lines).
- Assumptions/dependencies: accurate PoS mapping to subword tokens; latency trade-offs for on-the-fly classification.
- Sector: data engineering/ML training
- Use case: targeted data augmentation and curriculum for low-frequency/content tokens
- Description: boost representation of rare tokens and content categories (nouns/verbs) to reduce divergence; reorder curriculum to stabilize these categories during sharp-divergence phases.
- Tools/workflows: frequency-aware sampling; synthetic augmentation for rare terms; curriculum scheduling around phases identified by KL monitoring.
- Assumptions/dependencies: domain-specific data availability; potential side effects on generalization if overemphasized.
- Sector: academic research/analysis
- Use case: conditional convergence audits
- Description: replicate the paper’s conditional KL analyses (by frequency, PoS, final surprisal) to paper where models remain volatile and hypothesis-test interventions (regularization, data mixtures).
- Tools/workflows: reusable analysis pipeline; PoS-to-token mapping procedure (as described in the paper) for token-level diagnostics; regression analyses to quantify factor effects.
- Assumptions/dependencies: English PoS taggers; consistent tokenization; small evaluation subsets may limit statistical power.
- Sector: MLOps governance/compliance
- Use case: documentation of seed sensitivity
- Description: include stability metrics under varied seeds in model documentation; specify operational modes (“consistent mode” using ensembles vs “creative mode” with higher variance).
- Tools/workflows: updated model cards; procurement checklists requiring seed-stability thresholds for certain use cases; audit logs capturing seed details.
- Assumptions/dependencies: policy frameworks accepting quantitative stability measures; repeatability across versions.
- Sector: education and training (AI literacy)
- Use case: pedagogical modules on training dynamics
- Description: teach the four phases (uniform → sharp convergence → sharp divergence → slow reconvergence) and how they relate to unigram outputs and induction head formation; help students understand why cross-entropy improves even as cross-seed divergence rises.
- Tools/workflows: classroom visualizations; hands-on labs with MultiBERT/Pythia checkpoints; BLiMP-based downstream stability experiments.
- Assumptions/dependencies: access to open checkpoints and compute; English-centric examples.
- Sector: prompt engineering/product operations
- Use case: reliability-aware prompt design
- Description: when predictable, consistent behavior is needed, scaffold prompts to elicit function words/frequent patterns; for diverse content generation, accept higher variance or use ensembles.
- Tools/workflows: prompt templates emphasizing stable token classes; diagnostic prompts to detect instability spikes; routing policies based on stability metrics.
- Assumptions/dependencies: adherence of decoding behavior to token-level classes; trade-off between diversity and consistency.
- Sector: robotics and embedded AI
- Use case: stability checks for language-conditioned control
- Description: run cross-seed KL checks on command-generation modules; enforce ensemble or stricter decoding for action-critical tokens; avoid deploying small models if reconvergence is required.
- Tools/workflows: stability gates before policy updates; seed ensembles for instruction parsing; fallback to deterministic patterns for safety.
- Assumptions/dependencies: inference compute budgets on-device; latency constraints for ensemble inference.
- Sector: NLP evaluation (downstream tasks)
- Use case: task-level stability assessments on BLiMP-like datasets
- Description: measure convergence on reduced-support distributions (grammatical vs. ungrammatical pairs) to test seed stability in linguistic competence tasks; prefer checkpoints and sizes showing slow reconvergence.
- Tools/workflows: task-specific KL across seeds; per-task stability badges; checkpoint selection for deployment.
- Assumptions/dependencies: relevance of BLiMP-like tasks to production; limited early-step checkpoints for some suites (e.g., MultiBERT).
- Sector: compute planning/product strategy
- Use case: ROI-driven model sizing for stability
- Description: choose model size based on need for reconvergence and stable predictions; for non-critical tasks, accept smaller models that do not fully reconverge; for critical tasks, budget for larger models.
- Tools/workflows: cost–stability trade-off analysis; phase-aware training schedules; checkpoint selection protocols.
- Assumptions/dependencies: budget constraints; diminishing returns for very large models.
Long-Term Applications
These applications require further research, standardization, scaling, or engineering beyond current capabilities.
- Sector: standards/policy/regulation
- Use case: seed-stability certification for AI systems
- Description: define minimum cross-seed KL thresholds for specific domains (e.g., healthcare, finance); require reporting of token-class stability (function vs content, frequency bins).
- Tools/workflows: standardized test suites; model-card stability sections; external audits.
- Assumptions/dependencies: consensus on metrics and thresholds; sector-specific risk frameworks.
- Sector: model evaluation across architectures/tokenizers
- Use case: tokenizer-agnostic stability metrics
- Description: extend KL-based convergence to common supports (bytes or words) to compare different families (as noted in the paper’s limitations).
- Tools/workflows: distribution projection to byte/word levels; calibration methods; shared evaluation corpora.
- Assumptions/dependencies: robust projection techniques; validated fidelity across tokenization schemes.
- Sector: training algorithms/optimization
- Use case: stability-aware training schedules
- Description: adapt learning rates, regularization, and context usage during the identified sharp-divergence window to reduce seed-induced variability without harming generalization.
- Tools/workflows: phase detectors tied to convergence metrics; curriculum reshaping; loss reweighting for volatile token classes.
- Assumptions/dependencies: careful tuning to avoid overfitting; reproducible phase detection in diverse datasets.
- Sector: architectures/mechanistic interpretability
- Use case: targeted formation and stabilization of induction heads
- Description: design architectures or regularizers that promote earlier, more stable induction-head formation to accelerate reconvergence and in-context learning stability.
- Tools/workflows: mechanistic probes; head-level constraints; interpretability-guided training.
- Assumptions/dependencies: generality of induction-head dynamics across tasks; avoiding degraded capability.
- Sector: fairness and inclusivity in LLMs
- Use case: stability parity for rare or marginalized language
- Description: ensure models are equally stable on rare tokens and minority dialects; use conditional convergence audits to detect and remedy disparities.
- Tools/workflows: targeted data collection and augmentation; fairness audits with seed-stability metrics; governance reporting.
- Assumptions/dependencies: high-quality representative datasets; definitions of stability parity; cross-lingual coverage.
- Sector: knowledge distillation and compression
- Use case: distilling seed-ensembles into stable compact models
- Description: train a student model to match ensemble-averaged distributions, aiming to inherit low cross-seed variance while reducing inference costs.
- Tools/workflows: ensemble distillation pipelines; validation against stability benchmarks.
- Assumptions/dependencies: successful transfer of stability; managing diversity loss.
- Sector: adaptive inference systems
- Use case: stability-aware routing and decoding controllers
- Description: build controllers that detect volatile token classes or contexts and route to more conservative decoders or ensembles; switch modes based on predicted final surprisal bands.
- Tools/workflows: per-token volatility predictors; policy engines; hybrid decoding strategies.
- Assumptions/dependencies: reliable volatility prediction; latency budgets.
- Sector: multilingual NLP
- Use case: cross-lingual convergence profiling
- Description: extend conditional convergence analyses to other languages and multilingual models to characterize stability differences across scripts, morphology, and syntax.
- Tools/workflows: multilingual PoS taggers; language-aware token-frequency bins; shared benchmarks.
- Assumptions/dependencies: availability of comparable datasets; robust tagging/token mapping per language.
- Sector: dataset curation and governance
- Use case: convergence-informed corpus design
- Description: curate corpora to balance frequent and rare tokens; include contexts that reduce divergence for content words (e.g., richer semantic cues).
- Tools/workflows: dataset diagnostics via conditional KL; targeted corpus augmentation; governance boards for corpus changes.
- Assumptions/dependencies: avoiding dataset-induced biases; maintaining task relevance.
- Sector: reliability-driven product modes
- Use case: “stable” vs “creative” product settings
- Description: expose user-facing modes that toggle between ensemble-backed, low-variance outputs and single-seed, high-variance outputs; educate users about stability implications.
- Tools/workflows: UX flags; stability estimators surfacing to users; A/B tests on satisfaction vs consistency.
- Assumptions/dependencies: users understanding trade-offs; cost of supporting ensembles.
- Sector: adversarial robustness and red-teaming
- Use case: using divergence spikes as vulnerability signals
- Description: treat cross-seed divergence peaks as indicators of adversarial susceptibility; design tests that probe these contexts to harden models.
- Tools/workflows: stability-aware adversarial test suites; countermeasure training focused on high-variance tokens.
- Assumptions/dependencies: correlation between divergence and attack success; careful balancing to avoid over-regularization.
- Sector: automation of phase-aware training
- Use case: closed-loop controllers for training phase transitions
- Description: automate detection of phase boundaries (e.g., end of unigram stage, onset of sharp divergence, induction-head emergence) and adjust training hyperparameters accordingly.
- Tools/workflows: online convergence trackers; hyperparameter schedulers; reinforcement learning for training control.
- Assumptions/dependencies: reliable online metrics; generalization across datasets and architectures.
Cross-cutting assumptions and dependencies
- The KL-based convergence metric requires comparable output supports (same tokenizer); extensions to byte/word-level are needed for cross-family comparisons.
- Multi-seed training/checkpointing increases compute costs; some applications rely on ensembles or repeated training runs.
- Evidence in the paper is predominantly English and based on Pythia and MultiBERT suites; dynamics may differ in other languages, domains, and architectures.
- Early-phase dynamics may be affected by learning-rate warm-up schedules; care is needed when interpreting phase boundaries.
- Conditional analyses depend on accurate mapping from word-level PoS to subword tokens; mapping quality impacts interventions.
Glossary
- Autoregressive model: A LLM that predicts the next token by conditioning on previous tokens in a sequence. "The MultiBERT model suite is composed of bidirectional transformers---as opposed to Pythia's autoregressive models---and allows us to evaluate whether convergence dynamics are similar in such masked LLMs."
- BLiMP: A benchmark dataset of minimal pairs (grammatical vs. ungrammatical sentences) used to evaluate syntactic knowledge in LLMs. "BLiMP is a dataset composed of pairs of grammatical and ungrammatical sentences, and whose task is to identify the grammatical one."
- Conditional convergence: The expected similarity of model predictions across seeds, computed only for tokens or contexts with a specified property. "We quantify a model's conditional convergence as the expectation of convergence across tokens and contexts which have this property:"
- Content words: Semantically rich words (e.g., nouns, verbs, adjectives) that carry most of the meaning in a sentence. "function words achieve higher final convergence, whereas content words are more divergent."
- Cross-entropy: A measure of the average log loss of predicted probabilities against true outcomes; lower values indicate better fit. "Notably, the cross-entropy of Pythia models decreases monotonically throughout training (see \cref{fig:seeds-no-filters}, bottom)"
- Data-generating distribution: The underlying true probability distribution that produces the observed data. "At their core, LMs are distributions over strings, $\ptheta(\subwords)$, trained to approximate a data-generating distribution $\ptrue(\subwords)$."
- Distribution over model parameters: A probability distribution induced by architecture and optimization that captures variability across random seeds. "we first assume there exists a distribution over model parameters $\ptrue(\btheta)$, induced by a choice of architecture and the optimisation process."
- Downstream tasks: Evaluation tasks (beyond next-token prediction) used to assess model capabilities, often relating to application performance. "We now assess whether model convergence dynamics are similar in: (i) downstream tasks, conducting experiments on BLiMP"
- Effective rank: A measure of the dimensionality or complexity of representation spaces (often derived from singular values), used to characterize learned representations. "\citet{li2025tracingrepresentationgeometrylanguage} shows that the effective rank of LMs' representations presents similarly distinct phases across training."
- Expected convergence: The average convergence metric across contexts, summarizing overall similarity between models trained with different seeds. "We quantify expected convergence as the expectation of convergence across contexts:"
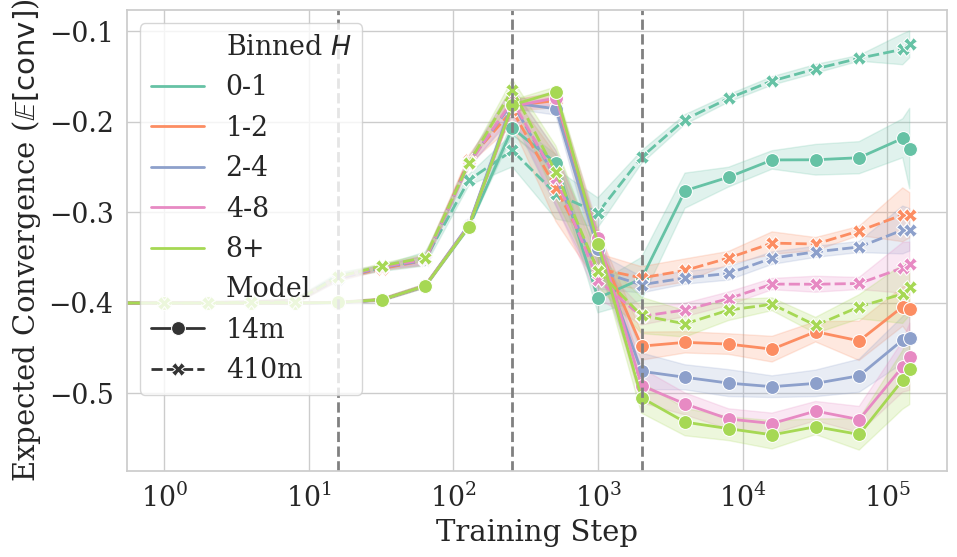
- Function words: High-frequency grammatical words (e.g., determiners, prepositions) that primarily serve syntactic roles. "Restricting our analysis to specific token frequencies or part-of-speech (PoS) tags further reveals that convergence is uneven across linguistic categories: frequent tokens and function words converge faster and more reliably than their counterparts (infrequent tokens and content words)."
- Induction head: A specific attention mechanism pattern in transformers that supports in-context learning by copying and matching tokens across positions. "This suggests that induction heads may not only enable in-context learning in large models, but also stabilise the training of transformer-based LMs."
- Induction-head formation: The emergence during training of attention heads that implement copying/matching behaviors supporting in-context learning. "Second, and also early in training, transformers go through induction-head formation, which enables in-context learning"
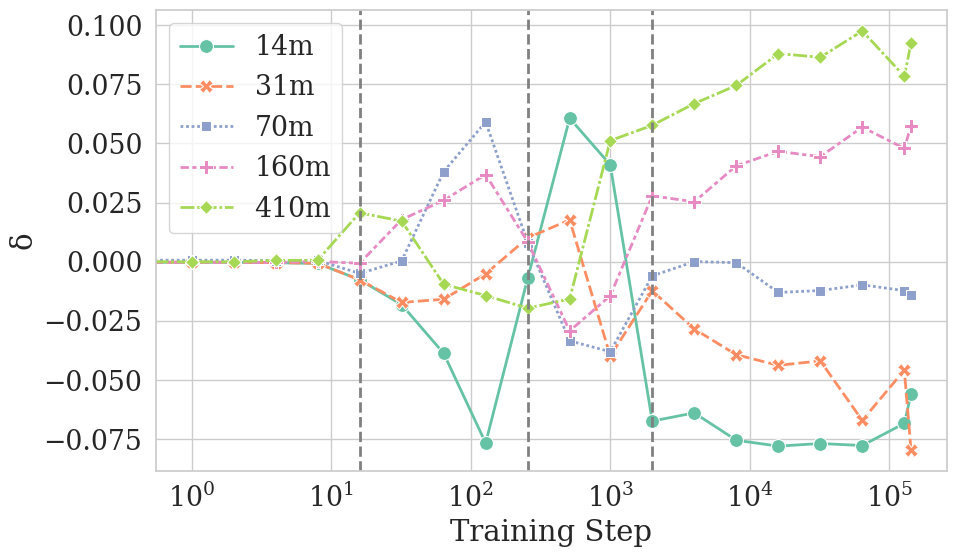
- In-context learning (ICL): The ability of a model to learn or adapt behavior from examples provided in its input context without parameter updates. "ICL scores were measured as the expected difference in surprisal of a sentence's 500 token when: conditioned on the preceding 50 tokens of context vs.\ on 400 tokens."
- Kullback–Leibler (KL) divergence: A non-symmetric measure of how one probability distribution differs from another; used here to quantify divergence across seeds. "Here, we will measure it as the Kullback-Leibler (KL) divergence:"
- Learning rate warm-up: A training schedule that gradually increases the learning rate during early steps to stabilize optimization. "the presence of learning rate warm-up phases during early training, where we observe the most rapid shifts in model behaviour, may introduce artifacts that affect our interpretation of convergence and divergence."
- Limited-support distribution: A probability distribution defined only over a restricted subset of outcomes (e.g., two candidate sentences). "We then use this limited-support distribution to compute models' convergence as in \cref{sec:convergence}"
- Masked LLM: A bidirectional model trained to predict masked tokens using both left and right context, unlike autoregressive models. "The MultiBERT model suite is composed of bidirectional transformers---as opposed to Pythia's autoregressive models---and allows us to evaluate whether convergence dynamics are similar in such masked LLMs."
- MultiBERT: A suite of BERT models trained with different seeds/configurations, enabling analyses of variability across runs. "The MultiBERT model suite is composed of bidirectional transformers"
- Part-of-speech (PoS) tags: Labels indicating the grammatical category of words (e.g., noun, verb, adjective) used to analyze convergence by linguistic class. "Restricting our analysis to specific token frequencies or part-of-speech (PoS) tags further reveals that convergence is uneven across linguistic categories"
- Platonic representations: Hypothesized idealized, modality-agnostic representations to which models may converge. "models not only converge in distribution, but all models across modalities will converge to true ``platonic representations''."
- PolyPythia: An extension of the Pythia suite providing multiple independently trained seeds per model size for variability analysis. "Luckily, \citet{wal2025polypythias} recently presented the PolyPythia model suite, an extension of the original Pythia model suite with multiple trained models---using different randomisation seeds---for each model size."
- Pythia: A family of transformer LLMs with standardized training procedures and multiple checkpoints across sizes. "The Pythia model suite includes model architectures of different sizes, and we analyse here models with parameters."
- Sharp-convergence phase: A training period characterized by a rapid increase in similarity across seeds. "there is a #1{sharp-convergence phase}"
- Sharp-divergence phase: A training period where similarity across seeds sharply decreases as models begin using context. "models follow a #1{sharp-divergence phase}, where they start learning to use context."
- Slow-reconvergence phase: A later training period marked by gradual re-alignment of predictions across seeds. "we see a #1{slow-reconvergence phase}, in which model predictions seem to stabilise and (at least for larger models) slowly reconverge to a unified solution"
- Support (of a distribution): The set of outcomes for which a probability distribution assigns non-zero probability. "In this task, we thus restrict the support of our models' distribution to these two sentences:"
- Surprisal: The information content of an event measured as the negative log probability; used to evaluate predictability. "ICL scores were measured as the expected difference in surprisal of a sentence's 500 token"
- Tokenisation: The process of splitting raw text into tokens (e.g., words or subwords) for model input. "because NLTK and Pythia employ different tokenisation methods"
- Unigram distribution: A probability distribution over tokens determined solely by their marginal frequencies, independent of context. "this phase corresponds quite clearly to a shift in LMs from mimicking a uniform to a unigram distribution."
- Unigram-output stage: An early training stage where models output distributions matching token frequencies without using context. "As discussed in \cref{sec:intro}, \citet{chang-bergen-2022-word} originally reported this unigram-output stage of LM learning."
- Uniform phase: The initial training period where outputs resemble a uniform distribution and convergence changes little. "After a short initial #1{uniform phase}, there is a #1{sharp-convergence phase}"
Collections
Sign up for free to add this paper to one or more collections.