Polychromic Objectives for Reinforcement Learning (2509.25424v1)
Abstract: Reinforcement learning fine-tuning (RLFT) is a dominant paradigm for improving pretrained policies for downstream tasks. These pretrained policies, trained on large datasets, produce generations with a broad range of promising but unrefined behaviors. Often, a critical failure mode of RLFT arises when policies lose this diversity and collapse into a handful of easily exploitable outputs. This convergence hinders exploration, which is essential for expanding the capabilities of the pretrained policy and for amplifying the benefits of test-time compute scaling. To address this, we introduce an objective for policy gradient methods that explicitly enforces the exploration and refinement of diverse generations, which we call a polychromic objective. We then show how proximal policy optimization (PPO) can be adapted to optimize this objective. Our method (1) employs vine sampling to collect on-policy rollouts and (2) modifies the advantage function to reflect the advantage under our new objective. Experiments on BabyAI, Minigrid, and Algorithmic Creativity show that our method improves success rates by reliably solving a larger set of environment configurations and generalizes better under large perturbations. Moreover, when given multiple attempts in pass@$k$ experiments, the policy achieves substantially higher coverage, demonstrating its ability to maintain and exploit a diverse repertoire of strategies.
Sponsored by Paperpile, the PDF & BibTeX manager trusted by top AI labs.
Get 30 days freePaper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about a problem in training AI using reinforcement learning: fine-tuning often makes a model “play it safe” and repeat just a few familiar solutions, instead of exploring many different ones. The authors propose a new way to fine-tune called a “polychromic objective” (polychromic means “many colors”), which encourages the AI to both succeed and keep a wide variety of strategies. They adapt a popular algorithm, PPO, to optimize this objective, and show it improves exploration, success, and generalization across several tasks.
What questions did the researchers ask?
- When we fine-tune a pretrained model with reinforcement learning (RLFT), how can we keep its broad set of skills and encourage it to discover new ones, instead of collapsing to a few repeated behaviors?
- Can we design an objective that rewards both “doing well” and “trying different” approaches at the same time?
- Will this objective lead to higher success when the model is given multiple attempts, and will it help the model handle changes or surprises in the environment?
How did they approach the problem?
First, some simple explanations of key ideas:
- Policy: The model’s strategy for choosing actions. Think of it like how a game-playing AI decides its next move.
- Trajectory: A complete “path” or sequence of moves from start to finish in a task.
- Diversity: How different those paths are from each other. More diversity means the AI tries various routes or plans.
- Entropy collapse: When a model stops exploring and only uses a few repeated tactics. It’s like always taking the same shortcut even when it doesn’t work everywhere.
The central idea is “set reinforcement learning”:
- Regular RL usually judges one trajectory at a time. Set reinforcement learning judges a set of trajectories sampled independently from the same starting state.
- The new “polychromic objective” scores a set based on two things: how successful the trajectories are and how diverse they are. In simple terms, a good set has wins and variety.
To make this practical, they modify PPO (a widely used RL method):
- Vine sampling: Imagine pausing a game at interesting checkpoints and trying many different continuations from that spot. This gives multiple trajectories from the same state so you can measure diversity and success together.
- Shared advantage signal: PPO needs a score called “advantage” that says how much better an action is than usual. Here, every action in the set from a rollout state gets the same advantage based on the whole set’s success and diversity. This pushes the policy to improve the overall quality and variety of its attempts, not just individual moves.
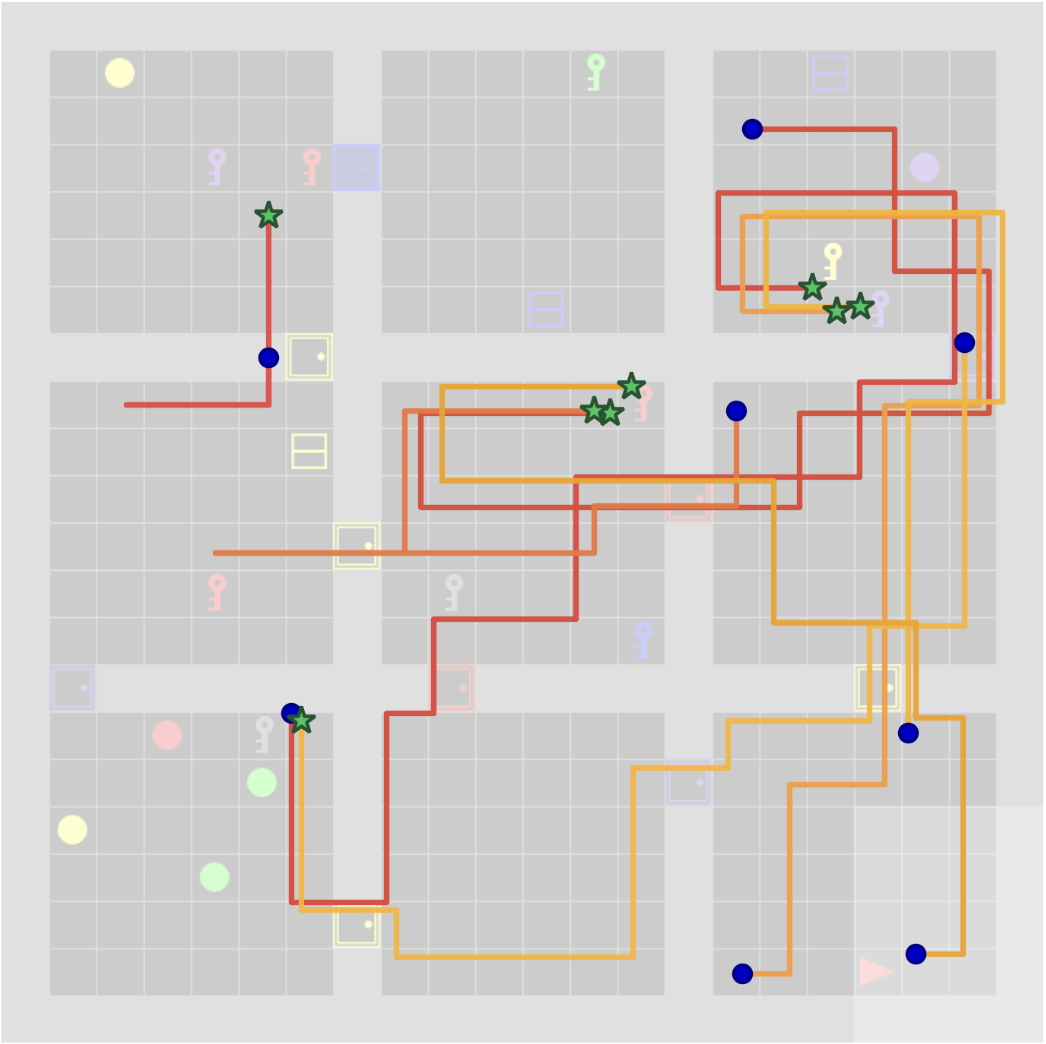
They also define a simple, plug-in diversity measure for each task, like “do these trajectories visit different rooms?” or “do they produce different triangles?” The method is flexible—you can swap in different diversity metrics.
What did they find?
Across three types of tasks—grid worlds (BabyAI, Minigrid) and a creativity task (finding triangles in graphs)—the results show strong benefits.
Key findings:
- Higher success without losing variety: The new method often matched or beat standard PPO and REINFORCE in reward and success rate on BabyAI/Minigrid tasks.
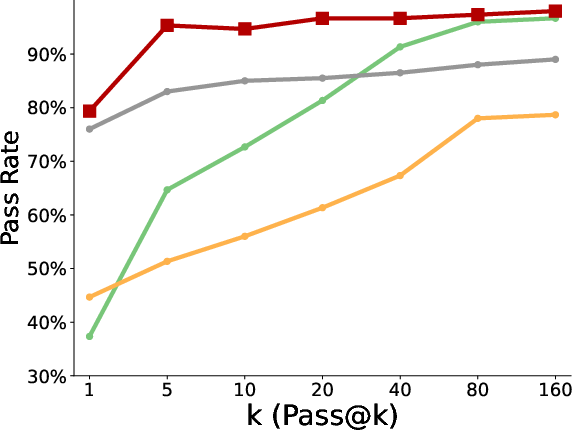
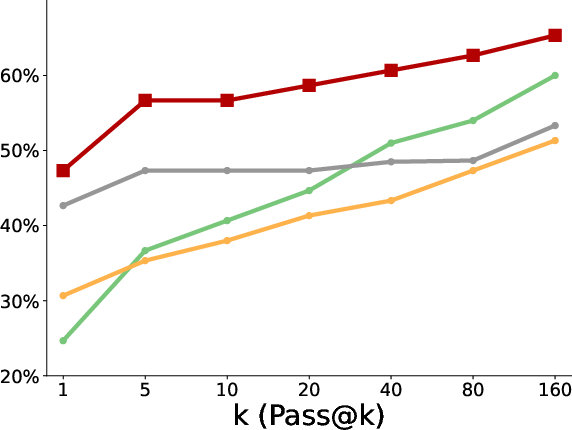
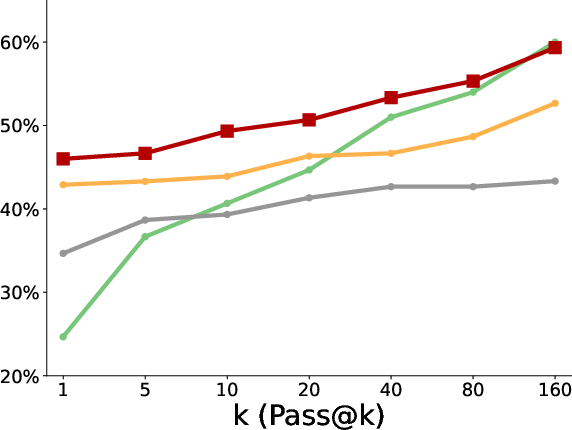
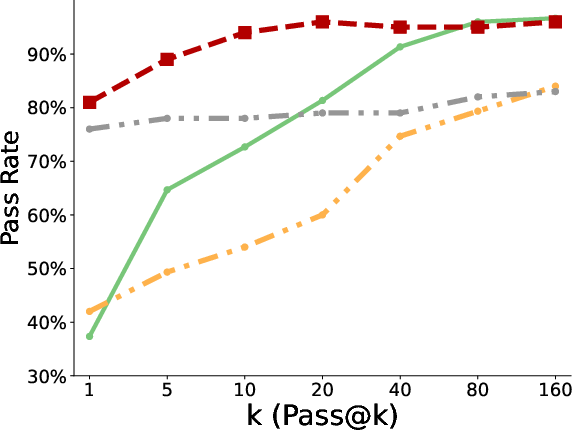
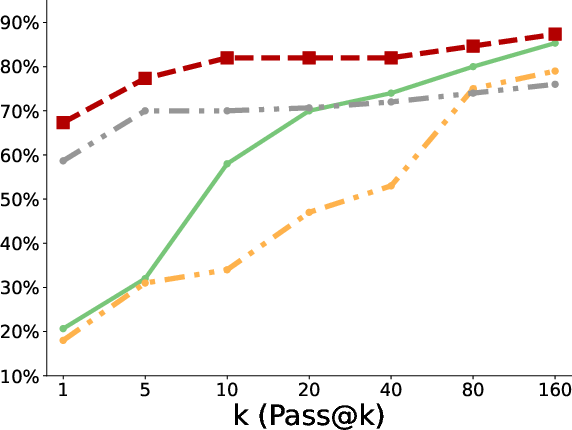
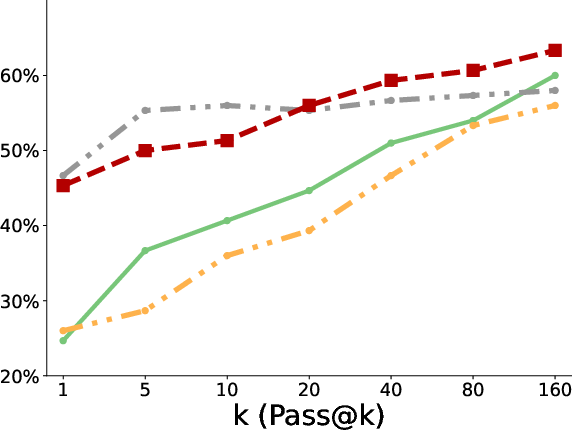
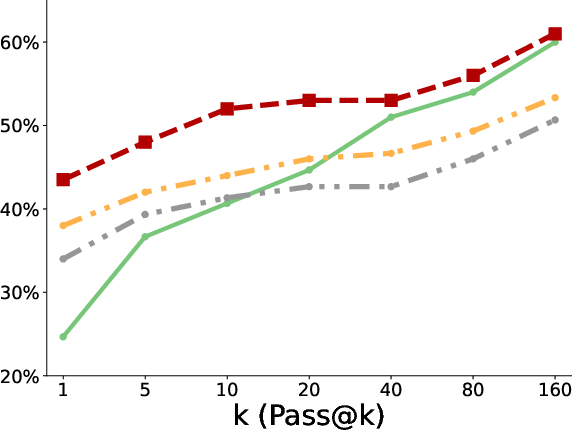
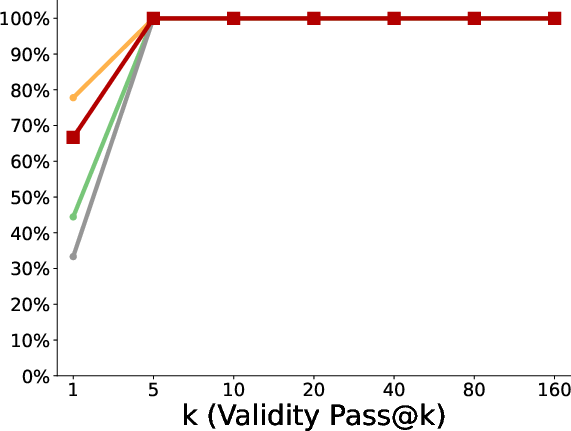
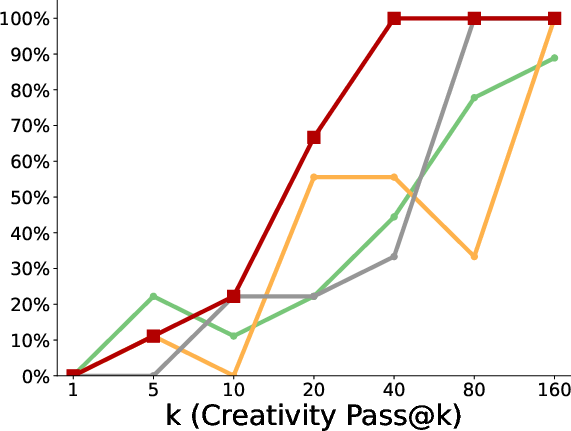
- Better pass@k coverage: “Pass@k” means the chance that at least one of k tries succeeds. With more attempts, the polychromic method kept improving, showing it maintained many different workable strategies. Standard RLFT often plateaued early or fell behind the original pretrained model at large k because it lost diversity.
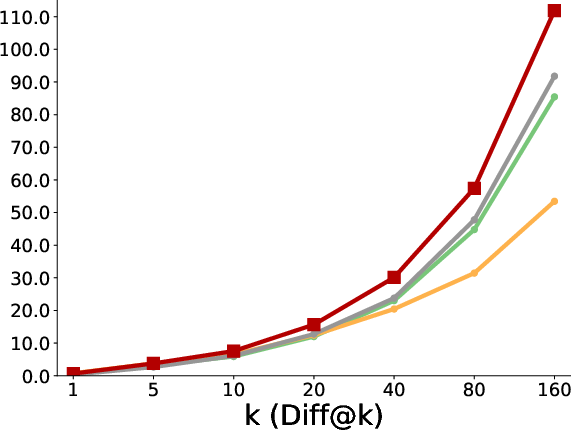
- More creativity and diversity: In the triangle discovery task, the polychromic method produced more unique, valid, and novel triangles (not seen during pretraining), demonstrating stronger exploration while still keeping good accuracy.
- Stronger generalization: When the starting state was perturbed (like starting in a different room), the polychromic method handled the change better, solving more cases than baselines. This suggests varied strategies help the model adapt to new situations.
They also provide a simple theoretical analysis:
- Under the polychromic objective, the model is less likely to collapse onto a single successful action over and over.
- Instead, it tends to favor sets that include multiple successful and different actions—exactly the balance of “win + explore” they want.
Why does this matter?
Many modern AI systems are pretrained on huge, diverse datasets and already “know” many kinds of strategies. Fine-tuning should refine these strategies, not erase them. The polychromic objective:
- Encourages exploration at the level of whole plans, not just small, random variations.
- Boosts success when you can afford multiple attempts, which is common in real-world use and test-time compute scaling.
- Improves robustness: diverse strategies help the model handle changes and unfamiliar situations.
- Is practical: it adapts PPO and works with standard environments and flexible diversity measures.
In short, this research shows a clear path to train AI that not only performs well but also keeps a rich toolbox of strategies—making it more creative, adaptable, and powerful in the long run.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single list of concrete gaps, limitations, and unresolved questions that future work could address:
- Generality of set RL: No convergence guarantees or sample complexity bounds are provided for set reinforcement learning (set RL) or polychromic PPO under realistic settings (long horizons, function approximation, PPO clipping), beyond an idealized extension of the performance difference lemma.
- Discount factor constraint: Theoretical value-function analysis imposes γ < 1/n to ensure boundedness, which is incompatible with standard practice (γ ≈ 0.99). It is unclear how to reconcile set-level returns with realistic discounting and whether alternative formulations avoid this restriction.
- Short-horizon entropy theory: Entropy analysis is limited to H = 1, discrete actions, binary rewards, softmax policies, and action-level diversity. Extending to trajectory-level, long-horizon, continuous action spaces, and non-binary rewards remains open.
- Scaffold-based collapse analysis: The covariance-based “scaffold” results are qualitative and rely on strong simplifying assumptions; empirical validation and generalization of these findings to realistic settings are missing.
- Multiplicative objective form: The chosen polychromic objective multiplies average reward by diversity, causing the signal to vanish when either component is near zero (especially under sparse rewards). Explore additive or other combinators, adaptive weighting, or gating schemes to avoid zero-gradient regions.
- Diversity metric dependence: The approach claims metric agnosticism but evaluates only domain-specific heuristics (rooms visited in gridworlds; nodes visited in graphs). Sensitivity to metric choice, robustness to noisy or mis-specified metrics, and guidelines for defining semantically meaningful diversity are not studied.
- Credit assignment within sets: Set RL enforces identical advantages for all trajectories in a set, potentially blurring credit assignment. Comparative experiments with trajectory-specific baselines (e.g., leave-one-out) and hybrid schemes are absent.
- Vine sampling requirement: The method depends on environment resets and vine sampling, limiting applicability to domains without reliable resets (e.g., real-world robotics, certain online systems). How to adapt polychromic PPO when resets are costly or impossible is unresolved.
- Vine coverage and bias: Criteria for selecting rollout states, ensuring sufficient vine coverage, and mitigating selection bias in vine sampling are unspecified. Analyze how vine design influences estimator bias/variance and performance.
- Baseline estimation validity: The value baseline at rollout states reuses the same pool of trajectories to form multiple sets; independence assumptions for unbiased estimation are unclear. Formal analysis of bias/variance trade-offs for M, N, n is missing.
- Hyperparameter sensitivity: No ablations on set size (n), number of vine rollouts (N), number of sets (M), KL penalty weight, PPO clip parameter, or learning rate. Provide scaling laws and sensitivity analyses for stability, performance, and diversity.
- Compute and sample efficiency: The additional rollouts per state and set-level updates increase training-time compute and environment interactions. Quantify the overhead and characterize compute-performance trade-offs relative to PPO and REINFORCE.
- Inference-time cost-benefit: Claims about improved pass@k and supporting test-time compute scaling are not paired with cost analyses (e.g., how many samples are needed for gains and at what inference cost). Provide utility curves relating k to coverage and cost.
- Baseline coverage: Comparisons exclude strong diversity-preserving baselines (e.g., max-entropy RL, sequence-level entropy regularization, KL to pretrained distribution, diversity-encouraging objectives, ensembles, population-based methods). A broader baseline suite is needed to isolate the unique contribution of polychromic PPO.
- RLHF/LLM applicability: Despite motivating RLFT for LLMs, no experiments on language tasks with human feedback, preferences, or verifiable reasoning are presented. Demonstrate applicability to RLHF, instruction following, and reasoning tasks at scale.
- Continuous control and robotics: Experiments are limited to discrete gridworlds and graph tasks. Applicability, stability, and data-efficiency in continuous control and real-world robotics are untested.
- Safety and reward hacking: Encouraging diversity can induce unsafe or undesirable behaviors. There is no analysis of safety constraints, robustness to adversarial exploration, or mechanisms to prevent reward hacking via artificial diversity inflation.
- Diversity-quality trade-off tuning: The observed trade-off (slightly lower validity with higher diversity) lacks principled controls. Develop methods to dynamically balance reward and diversity (e.g., adaptive weights, curriculum schedules, dual-objective optimization).
- Normalization choices: Both reward and diversity are normalized to [0,1], but the normalization scheme, its effect on learning dynamics, and cross-task comparability are not analyzed. Explore alternative scaling strategies and their impact.
- KL penalty details: The per-state KL penalty direction and weight are not justified or analyzed (e.g., D_KL(πβ||πθ) vs D_KL(πθ||πβ)). Study its role in stability and diversity preservation and compare with KL-to-pretrained regularization.
- Credit assignment vs PPO clipping: Polychromic advantages are set-level but PPO updates are action-level with clipping ratios. The theoretical implications of clipping under set-level advantages (e.g., monotonic improvement, bias) remain unexplored.
- Sparse reward regimes: The method claims to aid exploration in sparse-reward tasks, yet the multiplicative objective could suppress gradients when rewards are near zero. Evaluate performance in extreme sparsity and introduce mechanisms (e.g., exploration bonuses, optimistic value estimates) to bootstrap learning.
- Generalization evaluation design: Initial-state perturbations sample new starts from rooms the pretrained policy visited, potentially biasing the test distribution. Assess robustness under unbiased or adversarial perturbations and state distribution shifts.
- Diversity measurement validity: Distinctness defined by sets of rooms/nodes may conflate superficial and semantic diversity. Validate diversity metrics against downstream generalization and task success, or learn task-aware diversity representations.
- Statistical reporting: Results are averaged over seeds but lack error bars, confidence intervals, or significance testing. Provide statistical rigor to support claims, especially for pass@k curves and generalization under perturbations.
- Mode-collapse characterization: While pass@k improves, the method sometimes sacrifices pass@1; characterize when and why this occurs, and develop mechanisms to prevent collapse onto “broad but mediocre” behaviors.
- Negative rewards and constraints: The framework assumes nonnegative normalized rewards; handling negative rewards, constraints, and multi-objective settings (e.g., safety, cost) is not addressed.
- Adaptive or hierarchical sets: Fixed set sizes (n) and vine counts (N) may be suboptimal. Investigate adaptive set sizing, hierarchical polychromic objectives (e.g., subgoal-level diversity), and curriculum strategies to guide exploration.
- Interaction with UCB bonus: UCB regularization is treated as complementary, but its theoretical role and best practices (e.g., scaling with counts, interactions with set-level advantage) are not analyzed. Explore principled integration or alternative exploration bonuses.
Practical Applications
Overview
The paper introduces “polychromic objectives” for reinforcement learning fine-tuning (RLFT), optimized with a practical algorithm (Polychromic PPO) that:
- Treats optimization at the level of sets of trajectories (Set RL) instead of single rollouts.
- Encourages both high reward and semantic/trajectory-level diversity via a set-level diversity term.
- Uses vine sampling and a shared advantage to deliver a uniform learning signal across trajectories in a set, preserving diverse strategies and improving pass@k and robustness to state perturbations.
Below are actionable, real-world applications derived from these findings and methods, grouped by immediacy, with sector tags, potential tools/workflows, and feasibility assumptions.
Immediate Applications
These can be prototyped or deployed with today’s tooling, especially where environment reset/branching is available (e.g., simulation, text-based tasks, code-generation, offline/online RL setups with replay and controlled rollouts).
- LLM RLFT to preserve diversity without sacrificing quality
- Sectors: software, education, productivity, customer support
- Use cases:
- Code assistants and IDE copilots that train with polychromic PPO to improve pass@k (multiple attempts) while avoiding mode collapse (e.g., propose multiple compilable, semantically distinct fixes).
- Instruction following and reasoning assistants that maintain multiple solution paths; better success when given extra inference-time attempts.
- Tutoring systems that present diverse problem-solving strategies, not just a single “canonical” solution.
- Tools/workflows:
- Integrate polychromic PPO into existing RLHF/RLFT pipelines (e.g., TRL/DeepSpeed/RLlib) with a pluggable diversity metric: AST-difference or test-behavioral difference for code, embedding/Vendi Score for text, or constraint-based “distinct chain-of-thought” tags.
- Train-time objective: f_poly(s, τ1:n) = avg reward × diversity(τ1:n); inference-time: sample k solutions, rank/filter.
- Assumptions/dependencies:
- Ability to re-branch from partial generations (easy in text); availability of verifiable rewards (tests, rule-based validators, preference models).
- Compute overhead from vine sampling and multi-sample rollouts.
- Well-chosen diversity metric that reflects semantic, not just token-level, variation.
- Robust, diverse behavior for simulated robotics before deployment
- Sectors: robotics, manufacturing, logistics, home service
- Use cases:
- Sim training for manipulation or navigation with multiple viable strategies (grasp variants, navigation paths), improving robustness to initial-state perturbations and environment changes.
- Task libraries that benefit from diverse repertoires (e.g., door opening in different room layouts).
- Tools/workflows:
- Simulation (Isaac Gym/MuJoCo/Gazebo) with vine sampling; diversity metrics on state visitation (e.g., distinct room/region sets, path topology).
- Deploy best-of-k action sequences at runtime for harder tasks.
- Assumptions/dependencies:
- Resettable simulators; reward signals that approximate real-world success; sim-to-real gap still requires separate mitigation.
- Diversity-aware recommendation and ranking (top-N diversification)
- Sectors: media, retail, ads
- Use cases:
- Train contextual bandit/RL recommenders that explicitly optimize diversity within a set of suggestions while retaining click/conversion utility (higher “coverage” of user intents across top-N).
- Tools/workflows:
- Set-level objective with catalog/category/embedding diversity, calibrated with business KPIs; offline policy evaluation then gradual online rollout.
- Assumptions/dependencies:
- Mapping of diversity to business outcomes; careful counterfactual evaluation; possible adaptation from MDP to bandit with set-level return.
- Software testing and fuzzing with higher coverage
- Sectors: software, cybersecurity
- Use cases:
- RL-based test-case generators trained under polychromic objectives to maximize unique path/branch coverage across a set of test inputs per program state.
- Tools/workflows:
- Diversity = path-coverage signatures or CFG region coverage; rewards = crashes, new coverage; vine sampling by snapshotting execution states.
- Assumptions/dependencies:
- Efficient state checkpointing; reliable coverage measurement; guardrails against reward hacking.
- Creative content and design ideation
- Sectors: marketing, product design, gaming
- Use cases:
- Models that produce multiple distinct, on-brief concepts (ad copy variants, level designs) while keeping brand/constraint adherence.
- Tools/workflows:
- Reward from constraint/brand classifiers, human preference models; diversity via embedding dispersion or Vendi Score over outputs; human-in-the-loop selection.
- Assumptions/dependencies:
- Proxy rewards align with human judgment; scalable review workflow for multi-option outputs.
- Research tooling and evaluation standards
- Sectors: academia, open-source ecosystem
- Use cases:
- Reproducible baselines demonstrating pass@k and diversity metrics alongside reward/success.
- Open-source polychromic PPO modules with pluggable diversity functions and vine sampling.
- Tools/workflows:
- Add pass@k and diversity reporting to RLFT/LLM benchmarks; publish “diversity-aware RLFT” training recipes.
- Assumptions/dependencies:
- Community adoption; clear, normalized definitions of diversity per domain.
- Procurement and internal policy for AI buyers/developers
- Sectors: enterprise IT, public sector
- Use cases:
- Require reporting of pass@k, diversity metrics, and robustness-to-perturbation in evaluations for RLFT-based systems.
- Tools/workflows:
- Vendor checklists; model cards including diversity measures and perturbation stress tests.
- Assumptions/dependencies:
- Agreement on standardized metrics; availability of evaluation harnesses.
Long-Term Applications
These require additional research, scaling, safety validation, or domain approvals before broad deployment.
- Safety-critical decision support with multi-plan proposals
- Sectors: healthcare, autonomous driving, energy/grid control
- Use cases:
- Systems that generate several clinically/plausibly valid treatment or routing plans and surface trade-offs to human operators.
- Tools/workflows:
- Polychromic objectives with domain-specific diversity (e.g., mechanism-of-action or pathway diversity for treatments; route topology diversity for AV planning).
- Assumptions/dependencies:
- Regulatory approval, rigorous validation, causal safety analyses, robust human-in-the-loop oversight; strong guarantees against unsafe “exploration.”
- Drug and materials discovery with constrained diversity
- Sectors: biotech, materials
- Use cases:
- RL over generative chemistry that maximizes activity/ADMET reward and scaffold/chemotype diversity to avoid local optima and mode collapse.
- Tools/workflows:
- Diversity via Bemis–Murcko scaffolds, Tanimoto distances; rewards from predictive models + wet-lab feedback.
- Assumptions/dependencies:
- Reliable property predictors, high-fidelity assays, closed-loop lab automation; heavy compute and sample costs.
- Formal reasoning and theorem proving with diverse proof strategies
- Sectors: software verification, mathematics, safety certification
- Use cases:
- Agents that explore multiple distinct proof paths, improving pass@k on hard theorems/specifications.
- Tools/workflows:
- Branching from proof states (vine sampling in ITPs), diversity via proof-state embeddings or tactic-sequence uniqueness.
- Assumptions/dependencies:
- Tight integration with proof assistants; scalable reward signals; robust evaluation datasets.
- Multi-agent systems and self-play that avoid strategy collapse
- Sectors: cybersecurity (red/blue teaming), game AI, market simulations
- Use cases:
- Training regimes that maintain a repertoire of qualitatively different policies, improving robustness and meta-game coverage.
- Tools/workflows:
- Set-level objectives over joint policies/episodes; diversity across counter-strategies or exploitability metrics.
- Assumptions/dependencies:
- Computational scaling, stable training with many agents, new diversity metrics for interactions.
- Finance: portfolios of trading/logging policies with controlled diversification
- Sectors: finance
- Use cases:
- RL strategies that avoid collapsing onto a single regime, balancing PnL with portfolio-level diversity to reduce overfitting.
- Tools/workflows:
- Diversity via correlation structure or regime clustering of trajectories; cautious offline evaluation and guardrailed online rollout.
- Assumptions/dependencies:
- Strong risk controls, compliance review, extensive backtesting/live-sim; adversarial robustness.
- Real-world robotics with on-device multi-try inference and training
- Sectors: logistics, warehousing, manufacturing, home robotics
- Use cases:
- Robots that retain multiple strategies and pick the best of k at runtime in novel settings; training that minimizes catastrophic forgetting of viable alternatives.
- Tools/workflows:
- Sim-first training with polychromic PPO, then sim-to-real transfer; runtime selector to choose among diverse candidate plans.
- Assumptions/dependencies:
- Safety certification, latency constraints for k-sampling, robust sim-to-real transfer.
- Standards and governance for diversity-aware RLFT
- Sectors: policy, standards bodies
- Use cases:
- Best-practice guidelines mandating diversity/pass@k reporting for RLFT systems; audits to detect entropy collapse and brittle over-optimization.
- Tools/workflows:
- Compliance test suites, stress tests with initial-state perturbations, standardized diversity metrics by task.
- Assumptions/dependencies:
- Community consensus; impact assessments linking diversity to safety and fairness outcomes.
Cross-Cutting Dependencies and Assumptions
- Environment control: Vine sampling requires the ability to reset/branch from intermediate states (available in simulators, text/code generation, and many planning environments; harder in live, real-time systems).
- Diversity metrics: Must be domain-appropriate, normalized (0–1), and tied to semantic variation (examples: AST/behavioral difference for code; path/room coverage for robotics; embedding/Vendi Score for text; scaffold/Tanimoto for chemistry).
- Reward reliability: Needs verifiable or robust proxy rewards; guard against reward hacking and unintended shortcuts.
- Compute and data costs: Multi-sample rollouts and set-level training increase compute; careful batching, parallelization, and budget management required.
- Hyperparameters: Set size n and per-state samples N materially affect behavior; need tuning and monitoring of KL/clip penalties for stability.
- Complementary exploration: UCB-style bonuses can be combined with polychromic PPO; benefits are task-dependent.
- Organizational readiness: Teams must adapt evaluation to include pass@k, diversity, and robustness-to-perturbation reporting; may require product UX changes to surface multiple options to users.
Glossary
- Advantage function: In policy gradient methods, a quantity A(s,a) indicating how much better an action is compared to a baseline at a state; it guides the update direction. "modifies the advantage function to reflect the advantage under our new objective."
- Entropy collapse: A failure mode where a fine-tuned policy concentrates probability on a few behaviors, reducing diversity and exploration. "entropy collapse: instead of expanding their repertoire, fine-tuned policies concentrate probability mass on a narrow set of high-reward behaviors"
- Generalized Advantage Estimation (GAE): A variance-reduction technique that estimates advantages by exponentially weighting multi-step temporal-difference residuals. "using generalized advantage estimation (GAE)"
- Importance sampling: A technique to reweight samples collected from one distribution (policy) to estimate expectations under another. "Here, we use importance sampling to use actions sampled from ."
- Kullback–Leibler (KL) penalty: A regularization term using KL divergence to constrain how much the updated policy deviates from the behavior policy. "per-state KL penalty "
- Markov decision process (MDP): A formal framework for sequential decision-making defined by states, actions, transitions, rewards, and a discount factor. "We consider a Markov decision process defined by state space , action space , transition dynamics distribution , reward function ..."
- Multi-sample objective: An objective defined over sets of multiple sampled trajectories, rather than a single trajectory, to shape policies at the set level. "evaluated by a multi-sample objective"
- Pass@: A metric measuring the probability that at least one of k independently sampled rollouts succeeds. "the pass@ metric, which measures the probability that at least one out of independently sampled rollouts succeeds."
- Performance difference lemma: A result expressing the difference in value between two policies in terms of expected advantages under the new policy’s state visitation. "The following, known as the performance difference lemma, is a useful result"
- Polychromic objective: A set-level RL objective that jointly rewards success and diversity across a set of trajectories to encourage exploration. "we introduce an objective for policy gradient methods that explicitly enforces the exploration and refinement of diverse generations, which we call a polychromic objective."
- Polychromic PPO: A modified PPO algorithm that optimizes the polychromic objective using vine sampling and a set-based advantage. "Polychromic PPO"
- Proximal Policy Optimization (PPO): An on-policy policy-gradient algorithm that uses a clipped surrogate objective to constrain policy updates. "proximal policy optimization (PPO)~\citep{schulman2017proximalpolicyoptimizationalgorithms}"
- Reinforcement learning fine-tuning (RLFT): Applying reinforcement learning to further adapt pretrained models or policies to downstream tasks. "Reinforcement learning fine-tuning (RLFT) is a dominant paradigm for improving pretrained policies for downstream tasks."
- Scaffold value: A covariance-based quantity introduced to analyze where a policy is prone to concentrate probability mass over action sets under a set objective. "The scaffold value of a set of actions, , under a policy and a set-RL objective is defined to be"
- Set Q-function: In set RL, the expected return of the subtree starting from a state when a particular set of actions is taken at that state. "the set -function"
- Set reinforcement learning (set RL): A variant of RL where the objective is defined over sets of trajectories, providing a shared learning signal to all trajectories in the set. "We call this framework set reinforcement learning (set RL)"
- Set value function: In set RL, the expected discounted return of the entire state tree rooted at a state under a set objective. "the set value function"
- Softmax parameterization: A policy representation where action probabilities are given by a softmax over learnable logits. "We assume that our policy has a softmax parameterization."
- State-visitation distribution: The distribution over states induced by following a policy; often the stationary distribution used for expectations. "the stationary state-visitation distribution under policy ."
- State-visitation tree: The branching tree of states produced when multiple actions are sampled from each visited state in set RL analysis. "the data collection process naturally generates a state-visitation tree."
- TRPO: Trust Region Policy Optimization; a policy-gradient method that constrains updates via a trust region defined by KL divergence. "vine TRPO~\citep{schulman2017trustregionpolicyoptimization}"
- Upper Confidence Bound (UCB): An exploration strategy or bonus that encourages choosing less-sampled actions based on confidence intervals. "we compare with a UCB-style regularization"
- Vendi Score: A quantitative metric for diversity that measures the spread or evenness of a set of outputs. "the Vendi Score"
- Vine sampling: A rollout technique that spawns multiple independent trajectories from selected “rollout states” to form sets for on-policy updates. "we instead rely on vine sampling for on-policy data collection."
Collections
Sign up for free to add this paper to one or more collections.