Random Policy Valuation is Enough for LLM Reasoning with Verifiable Rewards (2509.24981v1)
Abstract: RL with Verifiable Rewards (RLVR) has emerged as a promising paradigm for improving the reasoning abilities of LLMs. Current methods rely primarily on policy optimization frameworks like PPO and GRPO, which follow generalized policy iteration that alternates between evaluating the current policy's value and improving the policy based on evaluation. While effective, they often suffer from training instability and diversity collapse, requiring complex heuristic tricks and careful tuning. We observe that standard RLVR in math reasoning can be formalized as a specialized finite-horizon Markov Decision Process with deterministic state transitions, tree-structured dynamics, and binary terminal rewards. Though large in scale, the underlying structure is simpler than general-purpose control settings for which popular RL algorithms (e.g., PPO) were developed, suggesting that several sophisticated techniques in existing methods may be reduced or even omitted. Based on this insight, we prove a surprising result: the optimal action can be recovered from the Q-function of a fixed uniformly random policy, thereby bypassing the generalized policy iteration loop and its associated heuristics. We introduce Random Policy Valuation for Diverse Reasoning (ROVER) to translate this principle into a practical and scalable algorithm for LLM math reasoning, a minimalist yet highly effective RL method that samples actions from a softmax over these uniform-policy Q-values. ROVER preserves diversity throughout training, allowing sustained exploration of multiple valid pathways. Across multiple base models and standard math reasoning benchmarks, ROVER demonstrates superior performance in both \textbf{quality} (\textbf{+8.2} on pass@1, \textbf{+16.8} on pass@256) and \textbf{diversity} (\textbf{+17.6\%}), despite its radical simplification compared to strong, complicated existing methods.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper looks at a simple way to train LLMs to solve math problems by using reinforcement learning (RL) with “verifiable rewards.” A verifiable reward means you can automatically check if the model’s final answer is correct or not (like grading a math problem). The authors propose a new, minimalist method called ROVER that is both easier to train and better at keeping diverse ways of reasoning, while still improving accuracy.
What question are the authors trying to answer?
They ask: “Are we using overly complicated RL tools for math reasoning when the problem’s structure is actually simpler? Can a much simpler method achieve high accuracy and still keep diverse thinking paths?”
In other words, they want a training method that:
- Improves the model’s reasoning quality (more correct answers),
- Avoids collapsing to one way of solving problems (keeps multiple valid solution paths),
- Is simpler and more stable than popular methods like PPO and GRPO.
How does their method work? (Explained with everyday analogies)
The setting: math problems as step-by-step decisions
Think of solving a math problem like walking down a tree of choices:
- Each step adds a word or symbol to the solution.
- Each choice leads to a new branch.
- There are no loops; you’re always moving forward.
- At the end, you get a simple reward: 1 if the final answer is correct, 0 if it’s wrong.
This structure is much simpler than typical RL tasks (like video games or robots), which often have loops, random changes, and rewards sprinkled along the way.
The key idea: value of a random policy
A “policy” is a rule for choosing actions. A “uniform random policy” just picks the next token completely at random, like rolling a fair die each time.
The surprising insight is this: if you measure, for each action, “what is the chance I’ll end up with a correct answer if I pick this action now and then continue randomly,” that number actually guides you to the best next step. This number is called a Q-value. So, even though the random policy itself is bad at solving problems, its Q-values give you a map of which branches are promising.
- Analogy: Imagine standing at a fork in a maze. For each path, ask, “If I choose this path and then wander randomly, what’s the chance I find the treasure?” Pick the path with the highest chance. That choice is, in this special kind of maze, the optimal move.
Greedy vs. diverse choices
- Greedy choice: Always pick the action with the highest Q-value. It’s optimal but can become too narrow, always following one solution style.
- Diverse choice: Use a “softmax” over Q-values. This means you still prefer better actions, but you sometimes try others. Think of it like weighted dice: actions with higher Q-values get more sides on the die, so they’re more likely to be chosen, but not guaranteed. A “temperature” knob controls how adventurous you are:
- Low temperature: very focused, almost greedy.
- High temperature: more exploratory, more diverse.
The authors prove that this softmax approach stays close to optimal while keeping diversity.
Making it practical for LLMs
Training Q-values from scratch is expensive. The trick:
- They reuse the LLM’s own scores (logits/probabilities) to represent Q-values “relatively,” comparing the current policy to the previous one. This stabilizes training.
- They reduce noise using “group reward centering”: sample several answers per question, compute the average reward, and center each answer’s reward around that average. Then they “broadcast” this signal to every token in the answer, so long solutions still learn effectively.
All of this forms ROVER: Random Policy Valuation for Diverse Reasoning.
What did they find, and why is it important?
Theory
- They prove that in math reasoning tasks (which form a deterministic tree with a correct/incorrect final check), you can find the optimal next action just by evaluating the Q-values of a fixed, uniform random policy and choosing the best. This avoids the usual complex loop of “evaluate, then improve” used by PPO/GRPO.
- Using softmax over these Q-values keeps solutions diverse while remaining near-optimal.
Experiments
They tested on:
- A “Countdown” puzzle task that has many correct paths,
- Competition-level math benchmarks (AIME 2024, AIME 2025, HMMT 2025, OlympiadBench, AMC 2023, MATH 500),
- An out-of-distribution test (GPQA diamond).
Main takeaways:
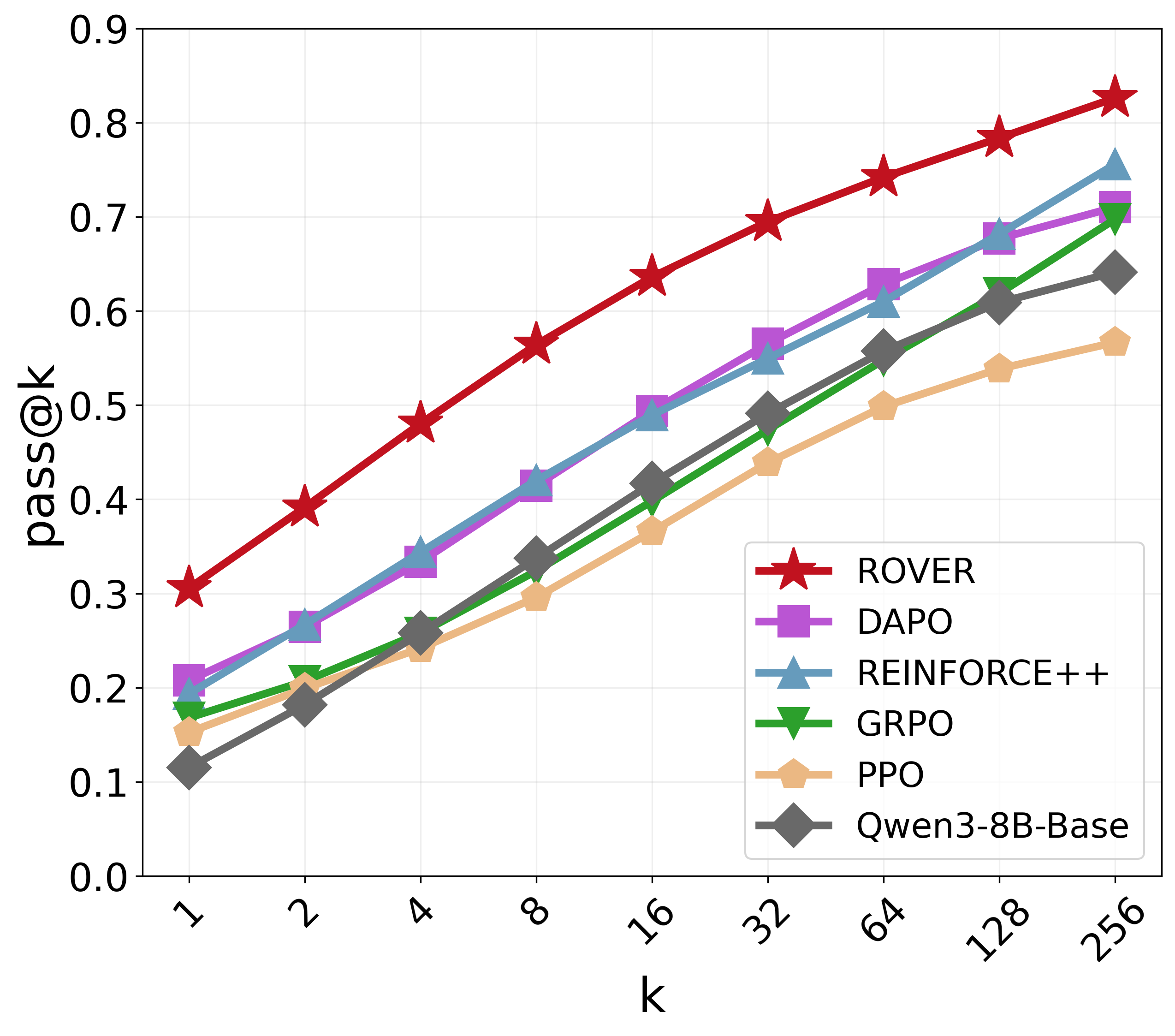
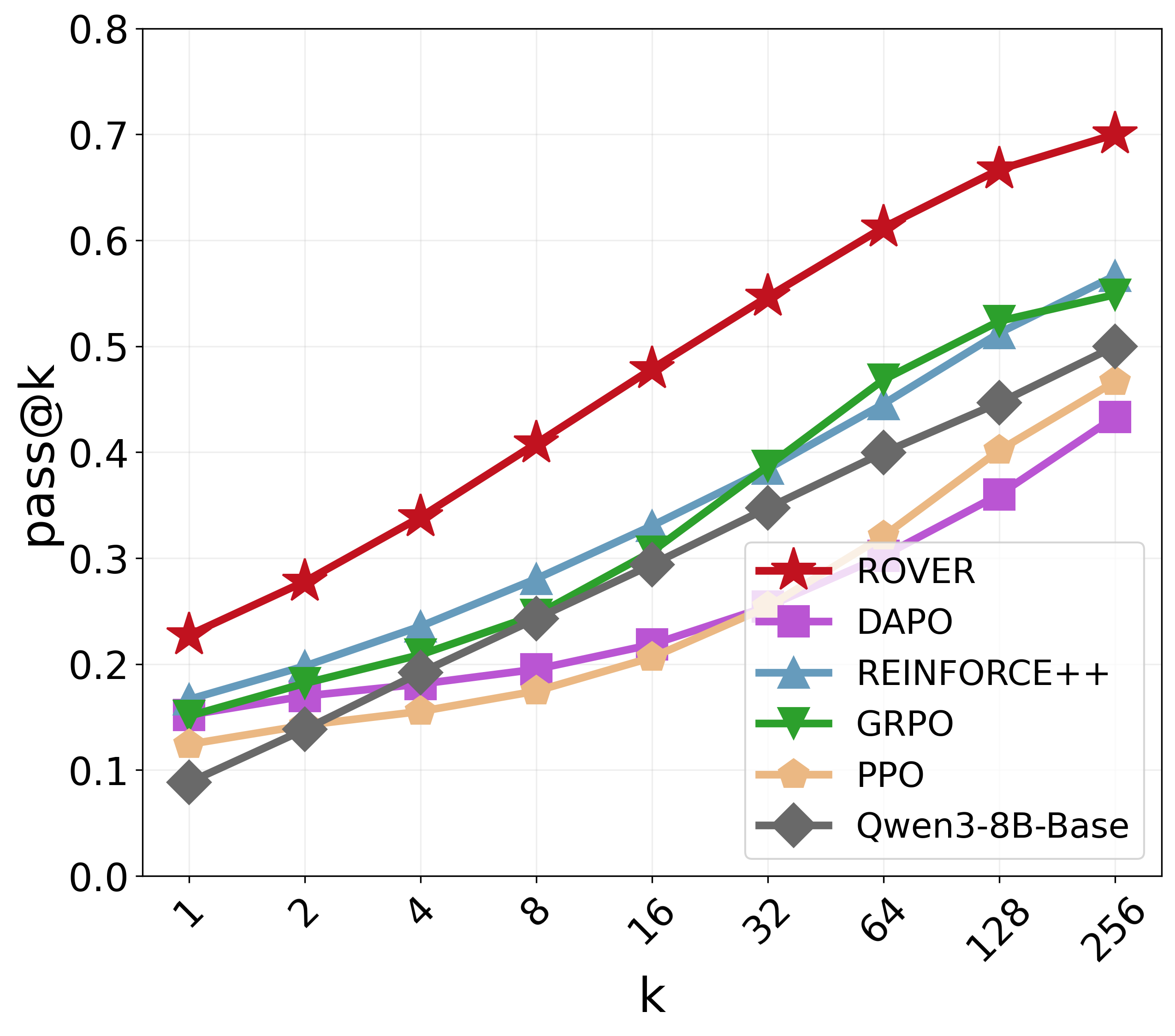
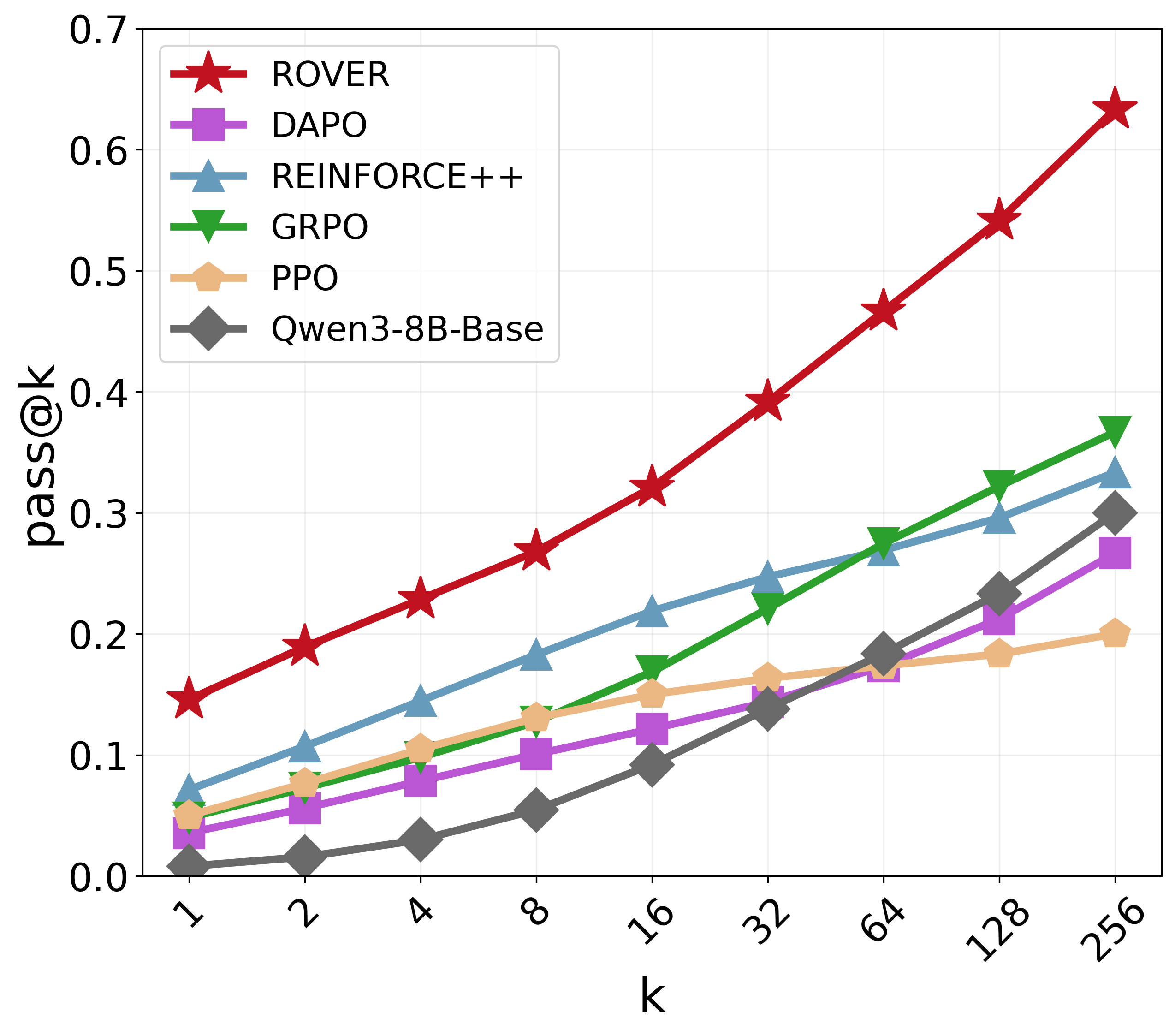
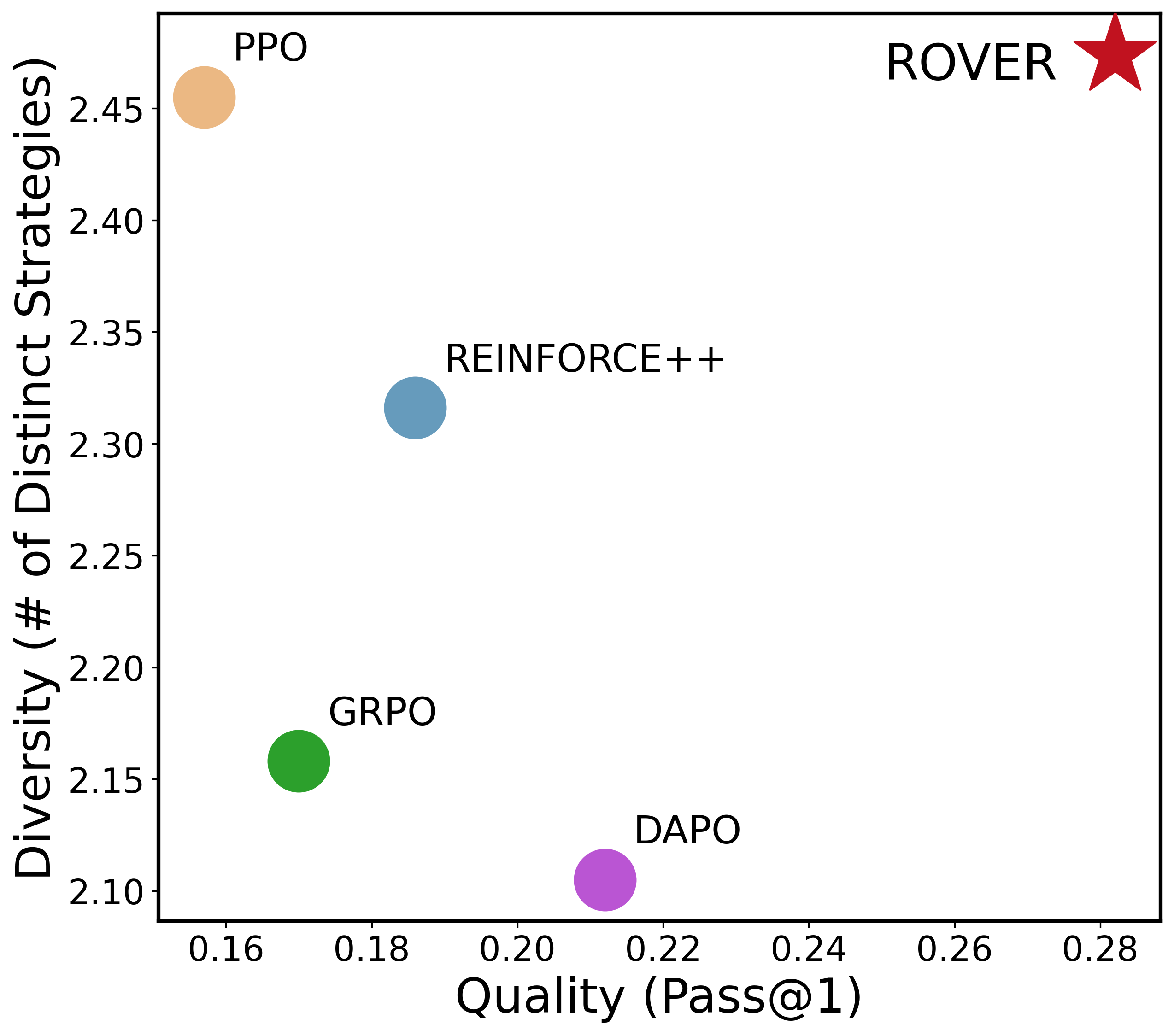
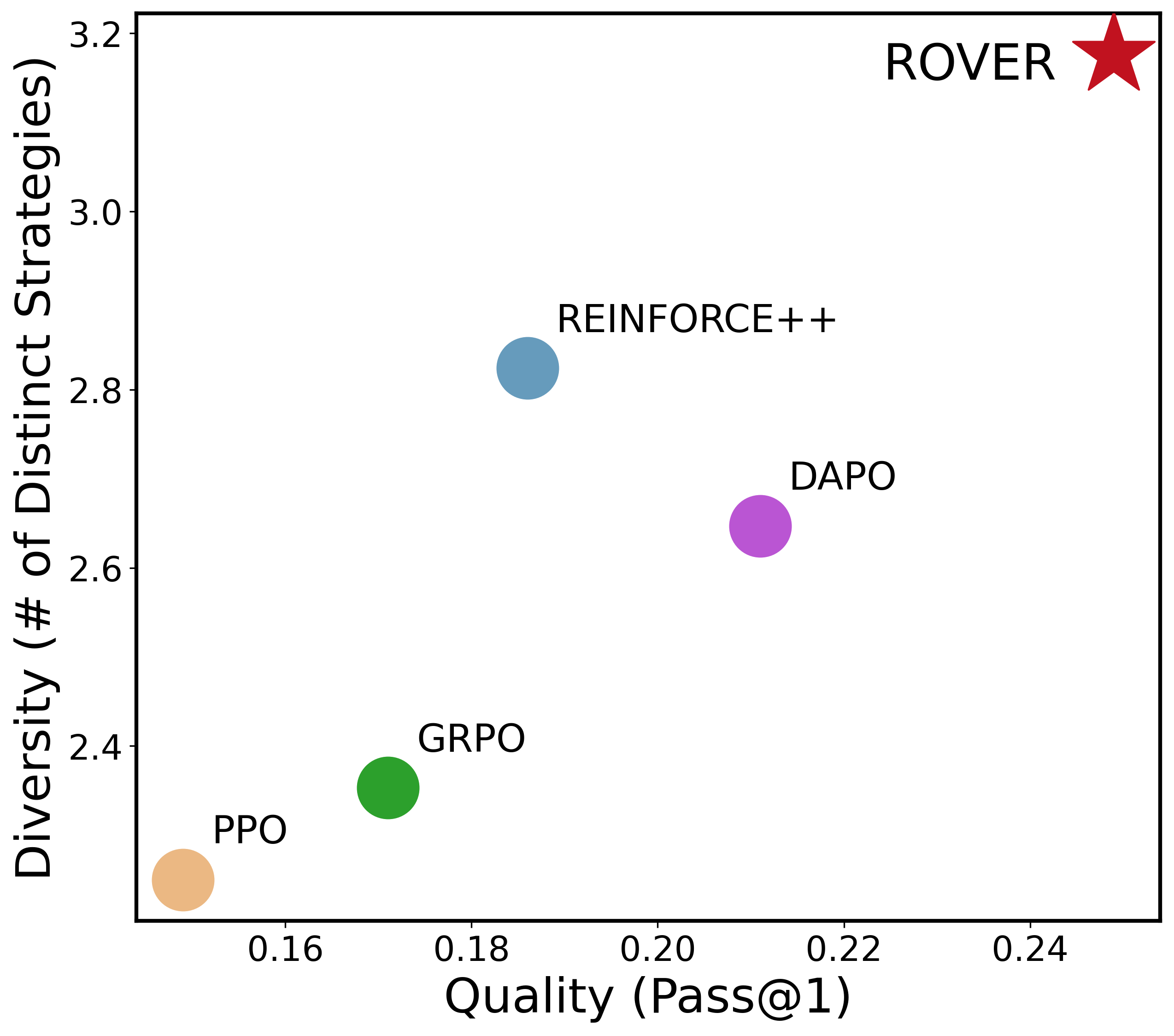
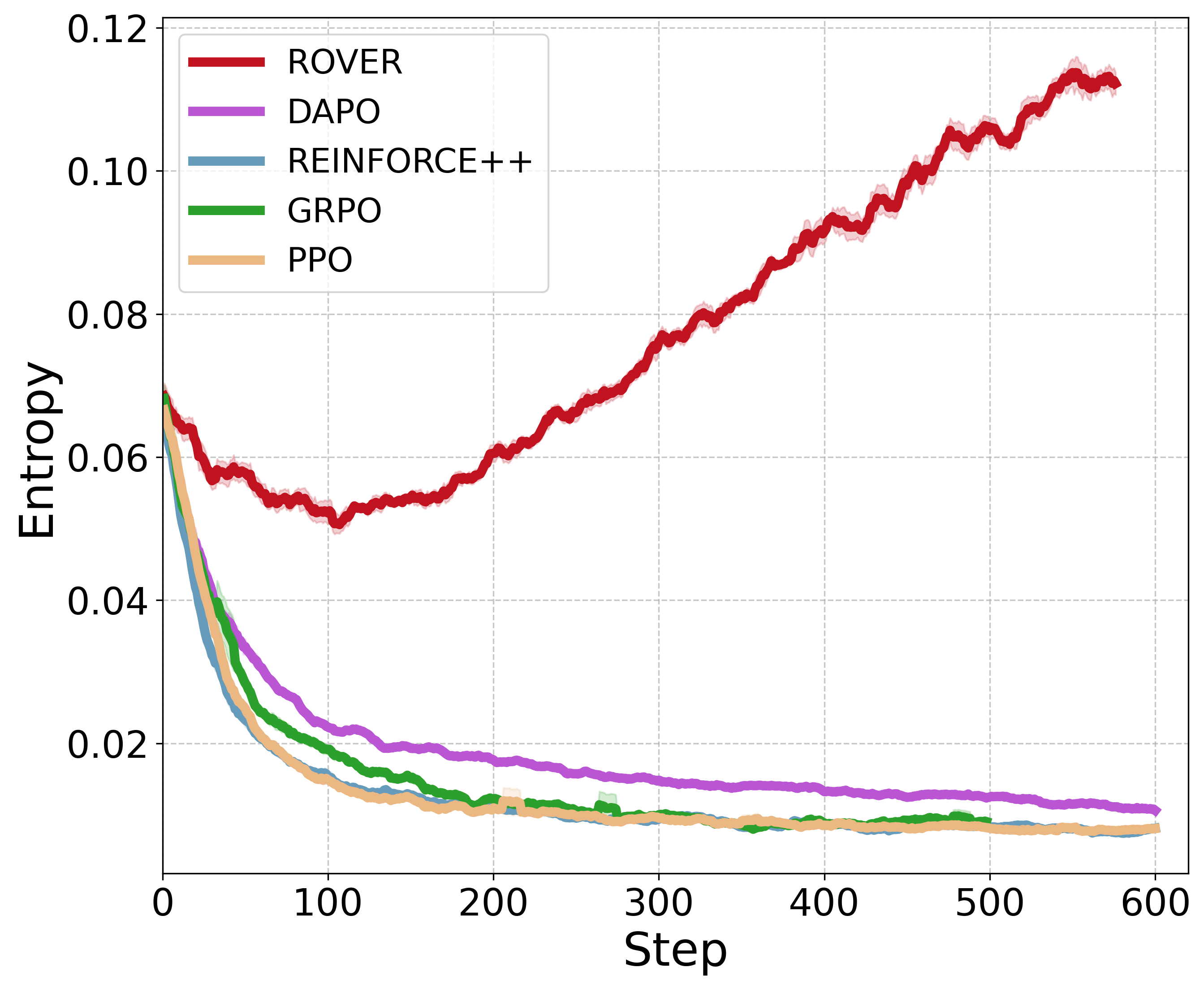
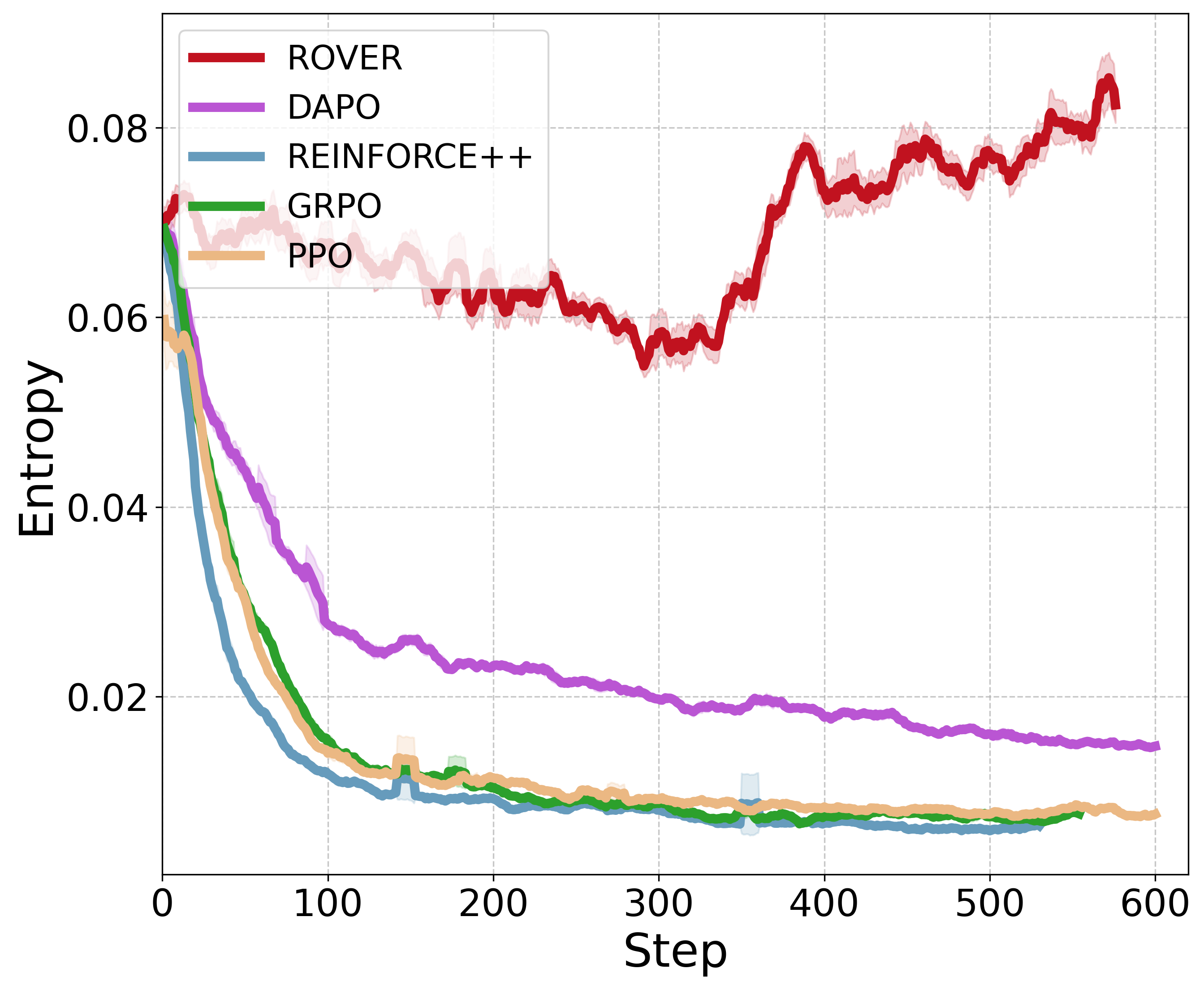
- ROVER consistently beats strong RL baselines like PPO, GRPO, REINFORCE++, and DAPO.
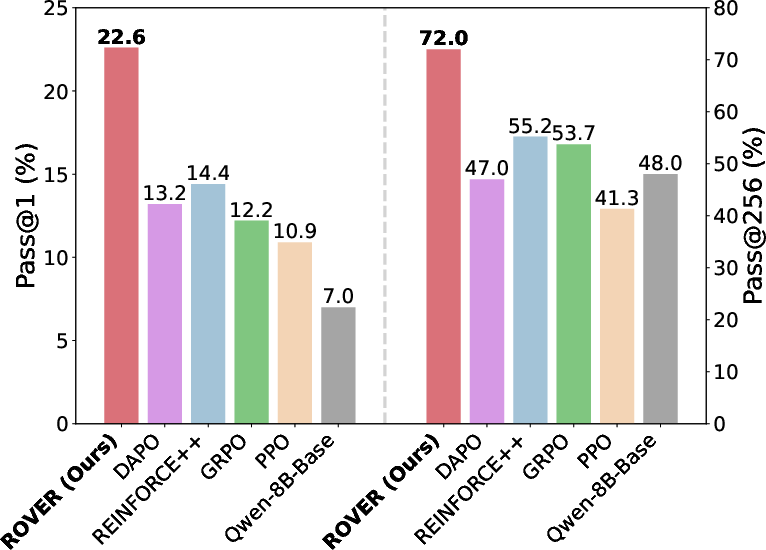
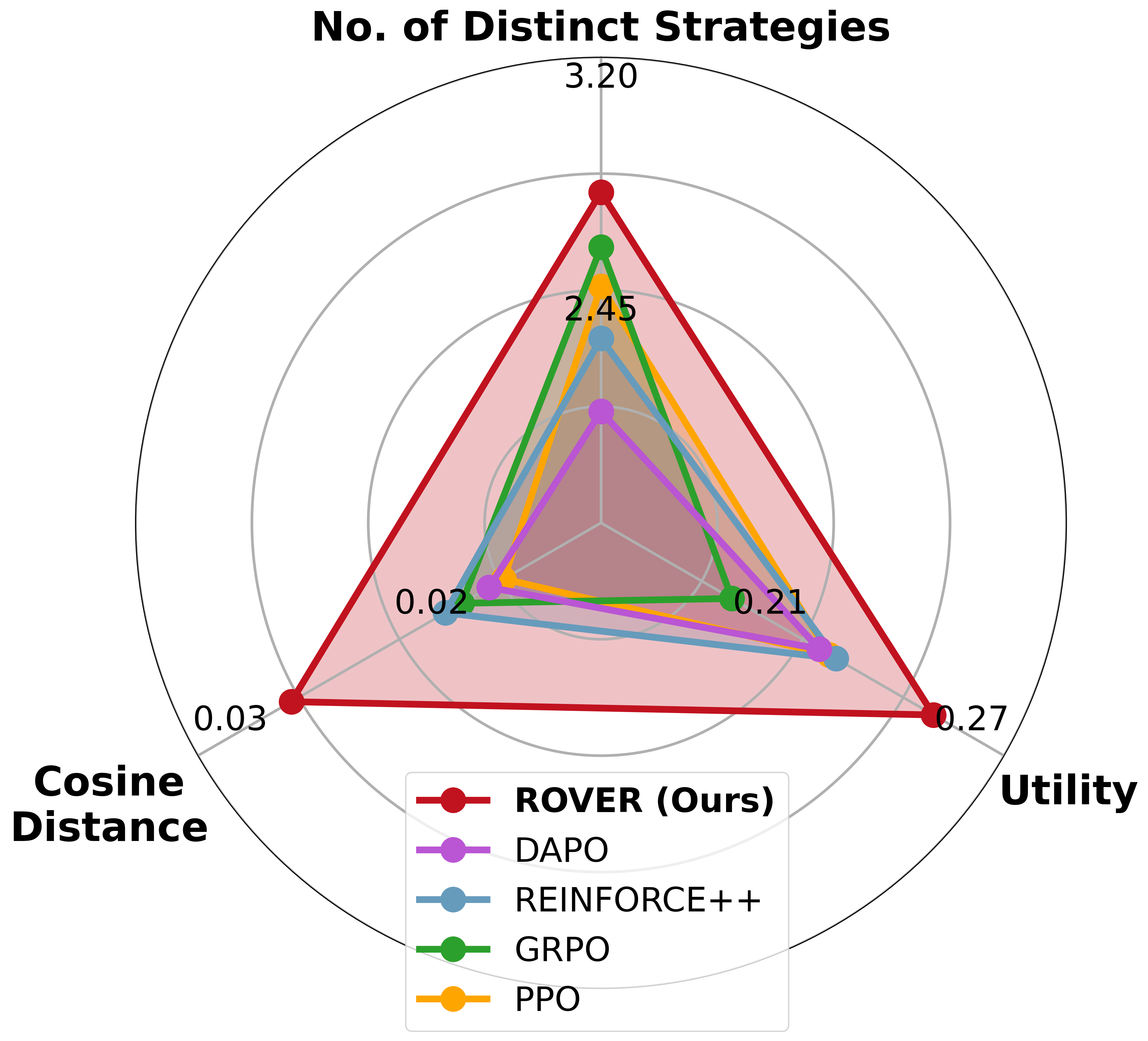
- On tough math benchmarks, it improves pass@1 by about +8.2 on average and pass@256 by +16.8, and increases diversity by about +17.6%.
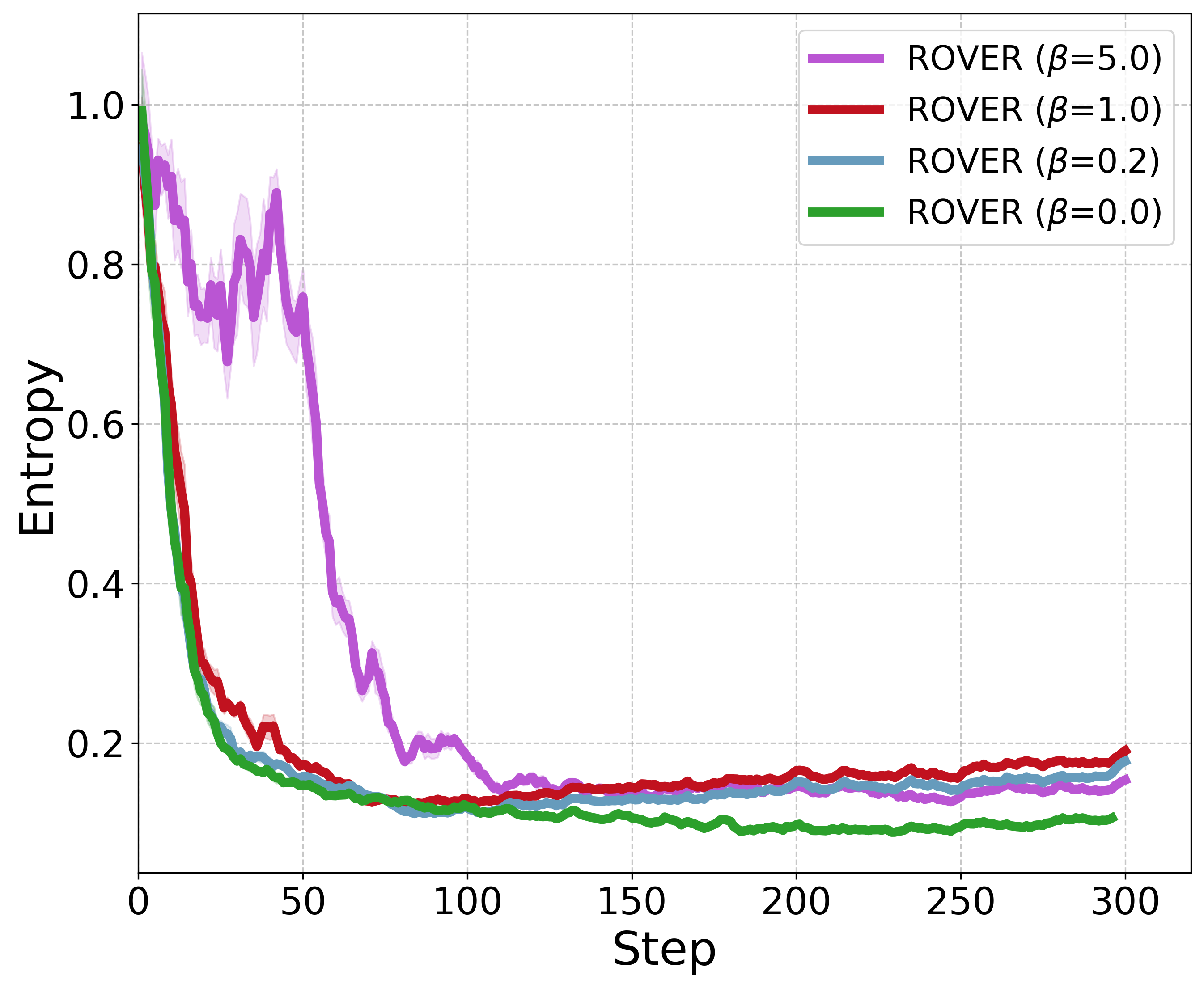
- On the Countdown task, it finds far more distinct correct solutions and keeps higher “entropy” (meaning the model explores and doesn’t get stuck in one pattern).
- It’s simpler to implement and avoids many tricky tuning steps used by existing methods.
Why this matters:
- Accuracy goes up,
- Diversity stays high,
- Training becomes simpler and more stable,
- The model discovers new reasoning strategies rather than memorizing one way.
What’s the broader impact?
If your task has a clear check at the end (like math answers, code tests, or puzzles), you can use ROVER to train LLMs:
- With fewer complicated tricks,
- With more stable training,
- With both better accuracy and richer solution styles.
This could make future AI systems more reliable at problem-solving and more creative, especially in areas where you can verify the result automatically. It’s a step toward simpler, stronger learning methods tailored to the structure of reasoning tasks.
Limitations to keep in mind:
- The theory relies on the task having a specific tree-like structure and binary “correct/incorrect” rewards. For more general RL settings (like messy, looping worlds), this exact approach may not apply.
Knowledge Gaps
Unresolved Gaps, Limitations, and Open Questions
Below is a concise, actionable list of what remains missing, uncertain, or unexplored in the paper.
- Theoretical scope is restricted to deterministic, tree-structured MDPs with binary terminal rewards; it is unknown whether the core result (optimality from uniform-policy Q-values) holds under:
- Stochastic transitions, cyclic or graph-structured state spaces, or shared/merged subtrees.
- Intermediate or shaped rewards, multi-valued rewards, partial credit, or delayed/non-terminal rewards.
- Task regimes beyond math reasoning (e.g., code generation, planning, tool-use) where verifiability or dynamics differ.
- Practical estimation of uniform-policy Q-values in large vocabularies is approximated by a mean operator and LLM log-prob differences; the paper does not quantify:
- Bias introduced by using samples from the current policy rather than a true uniform policy (no importance sampling or off-policy correction).
- The computational cost and feasibility of averaging over the full vocabulary at each step (whether top-k subsets or other approximations are used, and their impact on accuracy).
- The effect of function approximation error on the optimality guarantee and on the proposed softmax bound.
- The Q-parameterization as a relative log-prob difference drops state-dependent constants and relies on a moving baseline (θ_old); missing:
- A formal convergence analysis for this training objective under function approximation.
- Calibration/consistency guarantees (e.g., whether Q-values learned this way are properly scaled and comparable across states).
- Empirical or theoretical characterization of when this parameterization becomes unstable or biased.
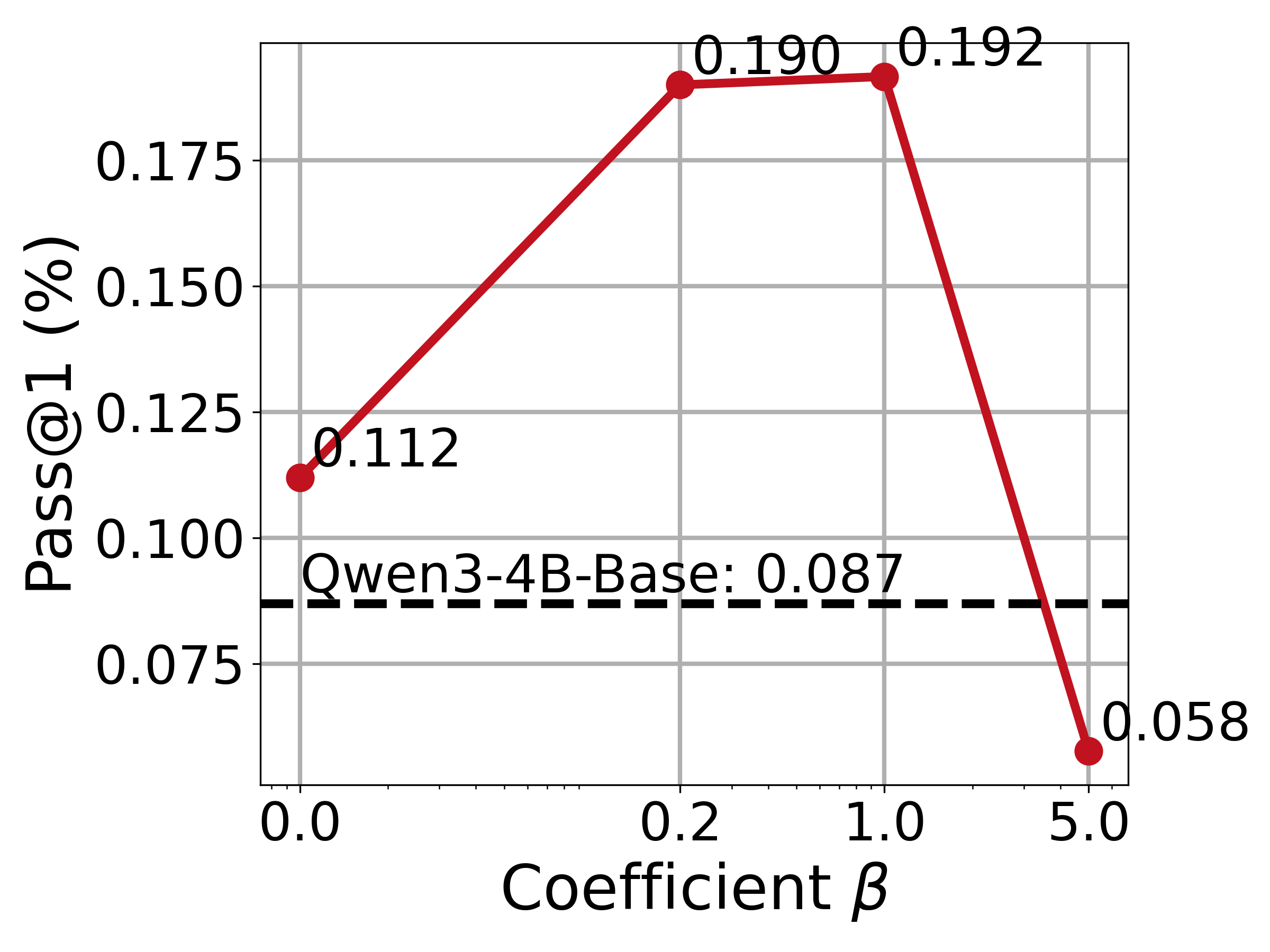
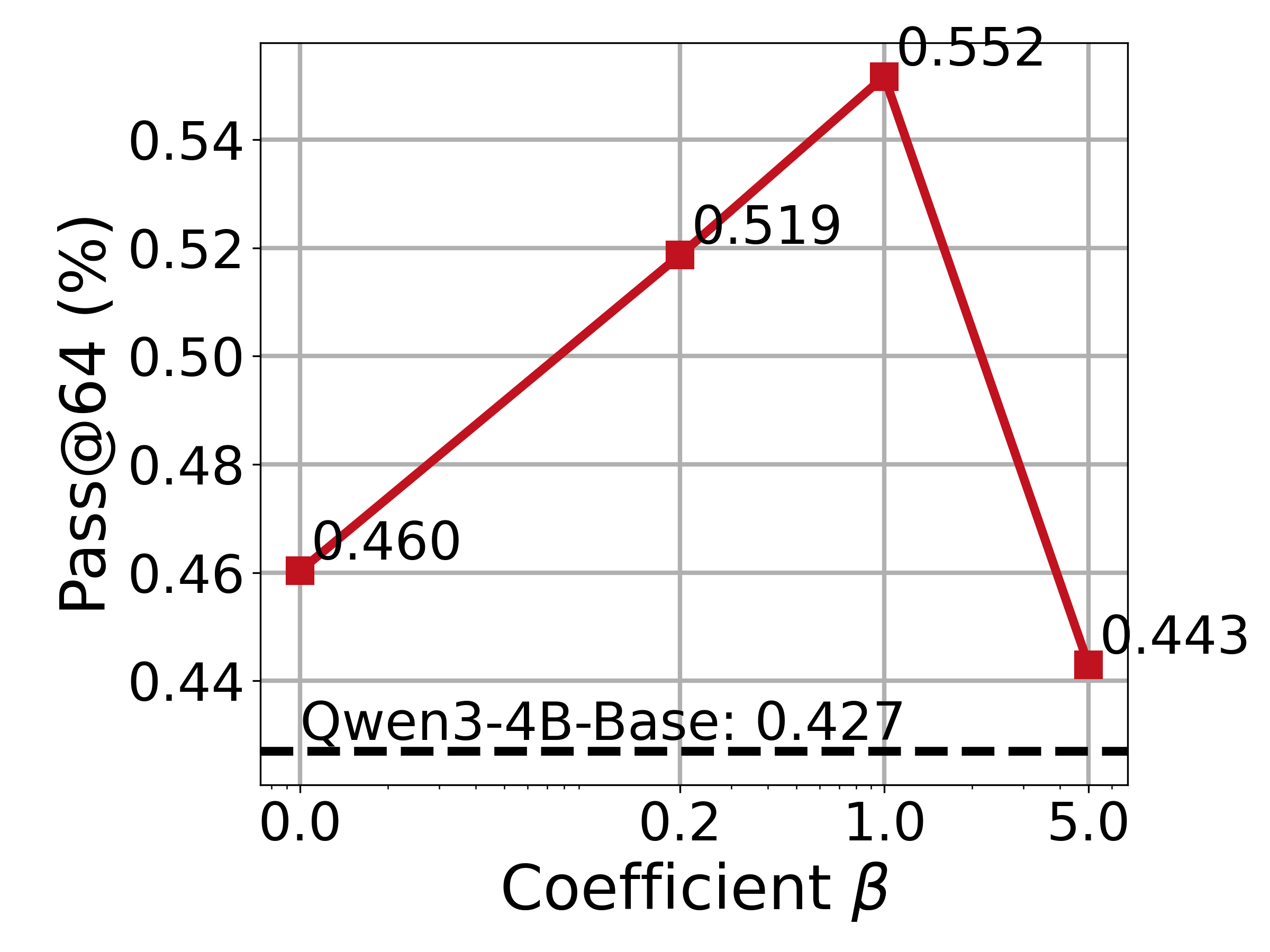
- The softmax temperature ρ is fixed (typically ρ=1) without a principled selection rule; open questions include:
- How to choose or adapt ρ per task, per state, or over training to optimize the quality–diversity trade-off.
- How to operationalize Theorem 2’s bound, which depends on unknown quantities (e.g., Pr{π_s}(s|s₀), N(s)); no practical estimator is provided.
- Decoding policy at inference is not fully specified or contrasted with standard LLM sampling:
- Whether actions are sampled from the learned Q-softmax or from the LLM’s logits, and how conflicts are resolved.
- How to integrate Q-softmax with common decoding controls (temperature, nucleus sampling, repetition penalties) without degrading guarantees.
- Diversity evaluation is task-specific and partly qualitative; gaps include:
- A standardized, reproducible way to measure “distinct solutions” across tasks (canonicalization of math expressions, equivalence checking, deduplication criteria).
- Evidence that increased diversity improves robustness and generalization beyond pass@k (e.g., against adversarial or OOD prompts).
- Reward modeling relies on a binary verifier (math_verify) and broadcasted rewards; unexplored aspects:
- Robustness to verifier noise, false positives/negatives, and imperfect parsing of solutions.
- Impact of reward broadcasting on credit assignment for long chains (potential over-attribution to early tokens).
- Extensions to richer, partially verifiable or heuristic rewards, and their effect on training stability.
- Training stability and fairness claims are not comprehensively substantiated:
- No convergence diagnostics (loss landscapes, gradient norms, variance) or multi-seed statistical tests are reported.
- Baseline tuning appears limited; controlled comparisons with equalized compute, batch sizes, and careful hyperparameter sweeps are missing.
- Ablations on key design choices (group size n, reward centering, vocabulary averaging strategy) are sparse.
- Sample efficiency and compute costs are not reported:
- No wall-clock, GPU-hours, or memory footprint comparisons versus PPO/GRPO/REINFORCE++.
- Scalability to larger models (>8B), longer horizons, and larger vocabularies remains unquantified.
- Generalization beyond math reasoning and RLVR is largely untested:
- Performance on diverse domains (e.g., programming, scientific reasoning, planning with tools/APIs) where rewards may be partial or non-verifiable remains unknown.
- Impact on non-reasoning capabilities and overall alignment/safety (catastrophic forgetting, hallucinations, harmful content) is not evaluated.
- The theoretical results rely on assumptions not guaranteed in practice:
- Availability of a well-defined action set per state (grammar constraints, special tokens, invalid actions) is not discussed.
- Deterministic transitions assume token concatenation only; tasks involving external tools, stochastic simulators, or environment feedback may violate this.
- Mode coverage analyses are limited to toy MDPs and countdown; missing:
- Rigorous, large-scale mode coverage studies on math datasets with formal equivalence checking and statistical significance.
- Analysis of whether coverage scales with model size and training length, and whether there are diminishing returns.
- Safety and undesirable-output risks from increased diversity are not assessed:
- No metrics or filters to ensure that diversification does not amplify irrelevant, misleading, or unsafe generations.
- Dataset and verifier dependencies are not stress-tested:
- Sensitivity to dataset composition (e.g., contamination, difficulty mix, prompt styles) and verifier changes is unreported.
- Transferability to different math verifiers or alternative benchmarks is not demonstrated.
- Extensions and connections to broader RL theory are underexplored:
- Relationship to maximum-entropy RL, soft Q-learning, and generalized policy iteration with alternative operators beyond mean/softmax.
- Conditions under which uniform-policy valuation remains near-optimal with partial observability or hierarchical policies.
Practical Applications
Immediate Applications
The following applications can be deployed now, leveraging the paper’s core findings: (1) optimal action selection from uniform-policy Q-values in tree-structured, deterministic, binary-reward MDPs; (2) the ROVER training algorithm that replaces complex PPO/GRPO loops with random policy valuation; and (3) practical techniques such as Q-parameterization via log-prob deltas, group reward centering, and reward broadcasting.
- LLM post-training for verifiable reasoning tasks
- Sector: software, education, research
- Use case: Replace PPO/GRPO in RLVR pipelines to fine-tune LLMs for math reasoning, code generation with unit tests, and SQL synthesis with schema/test constraints. Achieve higher pass@1 and pass@k while maintaining diversity and reducing training instability and implementation overhead.
- Tools/products/workflows: “ROVER Trainer” module integrated into existing RL frameworks (e.g., TRL/DeepSpeed), KL-free RL loops, group reward centering and reward broadcasting in token-level training, temperature-controlled softmax sampling over uniform-policy Q-values.
- Assumptions/dependencies: Availability of deterministic verifiers (e.g., math_verify, unit tests, SQL test suites), finite-horizon tree-structured generation (typical for autoregressive text), binary terminal rewards, pre-trained LLMs, and modest engineering to integrate ROVER into training pipelines.
- Math tutoring systems that present multiple valid solution paths
- Sector: education, edtech
- Use case: Train math assistants to produce diverse, correct solutions (step-by-step) for problems with unique or multiple answers, improving student understanding and pass@k outcomes (e.g., AIME/HMMT-style tasks, Countdown).
- Tools/products/workflows: Interactive tutoring apps that surface several reasoning strategies; classroom authoring tools for teachers that generate varied worked examples and hints; diversity-aware generation settings (temperature ρ≈1) to balance correctness and variety.
- Assumptions/dependencies: Problem sets with automatic graders/verifiers, institutional acceptance of AI-generated solutions, monitoring for pedagogical quality and explanation clarity beyond mere correctness.
- CI-driven code assistants that learn from tests
- Sector: software engineering
- Use case: Fine-tune code LLMs with ROVER to maximize test pass rates while preserving solution diversity (alternative implementations and patches). Useful for bug fixing, refactoring, and synthesis tasks where unit tests define binary success.
- Tools/products/workflows: “ROVER+CI” plugin that samples multiple candidate patches using softmaxed Q-values and ranks by test pass; a training loop that uses group reward centering over batch test outcomes.
- Assumptions/dependencies: Deterministic unit tests (pass/fail), scaffolding to run tests in training and inference, guardrails for code safety and licensing.
- Query and data-transformation synthesis with tests
- Sector: data engineering, analytics
- Use case: Train models to generate SQL queries, spreadsheet formulas, and ETL transformations verified by executable tests (expected outputs), achieving robust correctness and diverse alternative queries/plans.
- Tools/products/workflows: “Verified Query Synthesis” service that couples a ROVER-trained model with schema-aware test harnesses; diversity-preserving sampling to discover multiple correct queries for performance or interpretability trade-offs.
- Assumptions/dependencies: Well-specified test suites and expected outputs; deterministic evaluation environment; policies to select among diverse but equally correct outputs (e.g., performance or readability).
- Reproducible, audit-friendly RL baselines for academic labs
- Sector: academia
- Use case: Adopt ROVER to reduce complexity in RLVR studies, eliminate brittleness from KL clipping and heuristic scheduling, and improve experiment stability and reproducibility in math/code reasoning research.
- Tools/products/workflows: Minimal RLVR pipelines using uniform-policy evaluation; public benchmarks (AIME, HMMT, MATH500) and open-source verifiers; systematic ablations on temperature and group size; clearer training logs due to fixed-evaluation policy.
- Assumptions/dependencies: Access to verifiable benchmarks; willingness to prioritize tasks where binary rewards and deterministic transitions hold.
- Diversity-preserving inference settings for reasoning products
- Sector: software, education
- Use case: Deploy ROVER-trained models with softmax over uniform-policy Q-values to produce diverse solution attempts within pass@k inference workflows, increasing the chance of a correct solution on first try or within a small sample budget.
- Tools/products/workflows: “Pass@k Booster” decoding mode; ρ tuning defaults around 1; dashboards to measure solution diversity coverage and success probability.
- Assumptions/dependencies: Pre-trained ROVER models; tasks with verifiable success criteria; organizational acceptance of returning multiple candidates to users.
- Cost and energy reductions via simpler RL training
- Sector: industry, sustainability
- Use case: Reduce training cycles, tuning effort, and instability by replacing PPO/GRPO with ROVER for verifiable tasks, lowering compute costs and improving environmental footprint.
- Tools/products/workflows: KL-free, value-network-free pipelines; policy-evaluation-only training loop; standardized reward broadcasting and group centering.
- Assumptions/dependencies: Task fit (verifiable, deterministic, tree-structured), internal buy-in to simplify RL stacks.
Long-Term Applications
These opportunities will likely require further research, broader verifier coverage, scaling, domain adaptation, or policy/safety frameworks.
- Formal theorem proving and symbolic mathematics assistants
- Sector: software, academia
- Use case: Train models to produce formal proofs (e.g., Lean/Isabelle) where proof checkers serve as deterministic verifiers; leverage ROVER to discover multiple proof strategies and improve pass@k rates.
- Tools/products/workflows: “Formal Proof Coach” integrating proof checkers and ROVER; curriculum datasets of theorems with verified proofs; temperature schedules tailored to proof-space exploration.
- Assumptions/dependencies: High-quality formal datasets; robust, fast proof verifiers; careful handling of longer horizons and richer reward structures beyond binary correctness.
- Planning and scheduling with constraint solvers
- Sector: operations, logistics, energy
- Use case: Use constraint solvers (SAT/ILP) as verifiers to train planning agents for task assignments, routing, and grid scheduling; maintain diversity to surface multiple feasible plans (e.g., trade-offs in cost, risk, latency).
- Tools/products/workflows: “Verifier-First Planners” that couple LLM planning with formal verification; dashboards to compare diverse feasible plans; ROVER-based training on simulated planning datasets.
- Assumptions/dependencies: Reliable, deterministic solvers; mapping plans to binary feasibility checks; scaling to larger combinatorial spaces; domain-specific safety and regulatory constraints.
- High-level robotics task planning with formal verification
- Sector: robotics
- Use case: Apply ROVER to high-level plan synthesis (task graphs) with deterministic simulators or formal task validators; retain diverse plans for robustness and fallback strategies.
- Tools/products/workflows: “Plan+Verify” robotics pipelines; simulated environments with deterministic transitions; hybrid neuro-symbolic verification modules.
- Assumptions/dependencies: Deterministic or well-approximated simulators; verifiers capturing task constraints; bridging from symbolic correctness to physical execution under uncertainty (likely breaking strict determinism).
- Safety-constrained clinical or compliance assistants
- Sector: healthcare, finance, governance
- Use case: Where verifiers exist (e.g., guideline rule engines, compliance checkers), train assistants that propose diverse but compliant plans (care pathways, audit workflows), then filter via deterministic checks.
- Tools/products/workflows: “Compliance-First Reasoners” trained with ROVER; rule engines as binary reward signals; multi-strategy generation for human review.
- Assumptions/dependencies: Strong, trusted verifiers; clinical/financial safety approvals; rigorous human-in-the-loop oversight; careful handling of non-deterministic real-world factors.
- Multi-modal reasoning with simulators and verifiers
- Sector: education, engineering
- Use case: Extend ROVER to physics/chemistry problems using simulators to verify outcomes; encourage diverse solution paths (different modeling assumptions or derivations).
- Tools/products/workflows: “Simulator-Verified Tutors” for STEM; curated multimodal datasets; ROVER training adapted to longer horizons and graded rewards.
- Assumptions/dependencies: Fast, reliable simulators; mapping outcomes to binary/graded rewards; careful calibration for non-binary signals.
- General-purpose “Verifier API” ecosystem for RLVR training
- Sector: software platforms
- Use case: Build standardized APIs for plugging domain verifiers (tests, solvers, proof checkers) into ROVER-style training at scale, lowering barriers to building verifiable-reward tasks across industries.
- Tools/products/workflows: Hosted verifiers, sandboxed execution, telemetry on success probabilities, temperature management utilities, diversity metrics tracking.
- Assumptions/dependencies: Community and vendor support; security and sandboxing for test execution; cost-effective infrastructure.
- Policy and governance for reproducible, energy-efficient AI training
- Sector: policy, public sector
- Use case: Encourage “verifier-first” RL training for public models and education tools, emphasizing simpler, audit-friendly methods (like ROVER) that reduce complexity and compute load.
- Tools/products/workflows: Procurement guidelines, reproducibility standards, sustainability reporting frameworks that recognize verifier-backed training loops and diversity-preserving decoders.
- Assumptions/dependencies: Policy consensus, standardized benchmarks and reporting, attention to equity and academic integrity.
- Research directions to generalize beyond binary, deterministic trees
- Sector: academia
- Use case: Extend theory and algorithms to stochastic transitions, non-tree graphs, and non-binary rewards; develop temperature schedules with performance guarantees; combine ROVER with search (e.g., MCTS) for large reasoning spaces.
- Tools/products/workflows: New operators that preserve diversity and stability; hybrid verifiers (graded scoring); open-source libraries and benchmarks.
- Assumptions/dependencies: Novel theoretical results, robust empirical validation in diverse domains, community adoption.
Glossary
- AdamW optimizer: A variant of Adam that decouples weight decay from gradient-based updates for better regularization. "by an AdamW optimizer"
- Advantage function: A quantity estimating how much better an action is than the average at a state, used to reduce variance in policy gradients. "A_t is the advantage of current action."
- Autoregressive generation: Token-by-token sequence generation where each token depends on previous tokens. "This autoregressive generation continues until forming an entire response y={a0,a1,···,a|y|−1}, and finally receives a verifiable reward r(x,y)∈{0,1}."
- Behavior policy: The policy used to generate data for training or evaluation. "where $\pi_{\theta_{\rm old}$ is the behavior policy used to sample data in each epoch, serving as a stable anchor that reduces fluctuations."
- Binary terminal rewards: Rewards given only at episode termination that take on one of two values (e.g., correct/incorrect). "binary terminal rewards (correct or incorrect)"
- Broadcast the reward: Assigning the same reward to all tokens or steps of a trajectory to improve learning efficiency. "and broadcast the reward to improve training efficiency."
- Catastrophic forgetting: Rapid loss of previously learned knowledge when training continues on new data or objectives. "to prevent catastrophic forgetting and maintain exploration during continual learning"
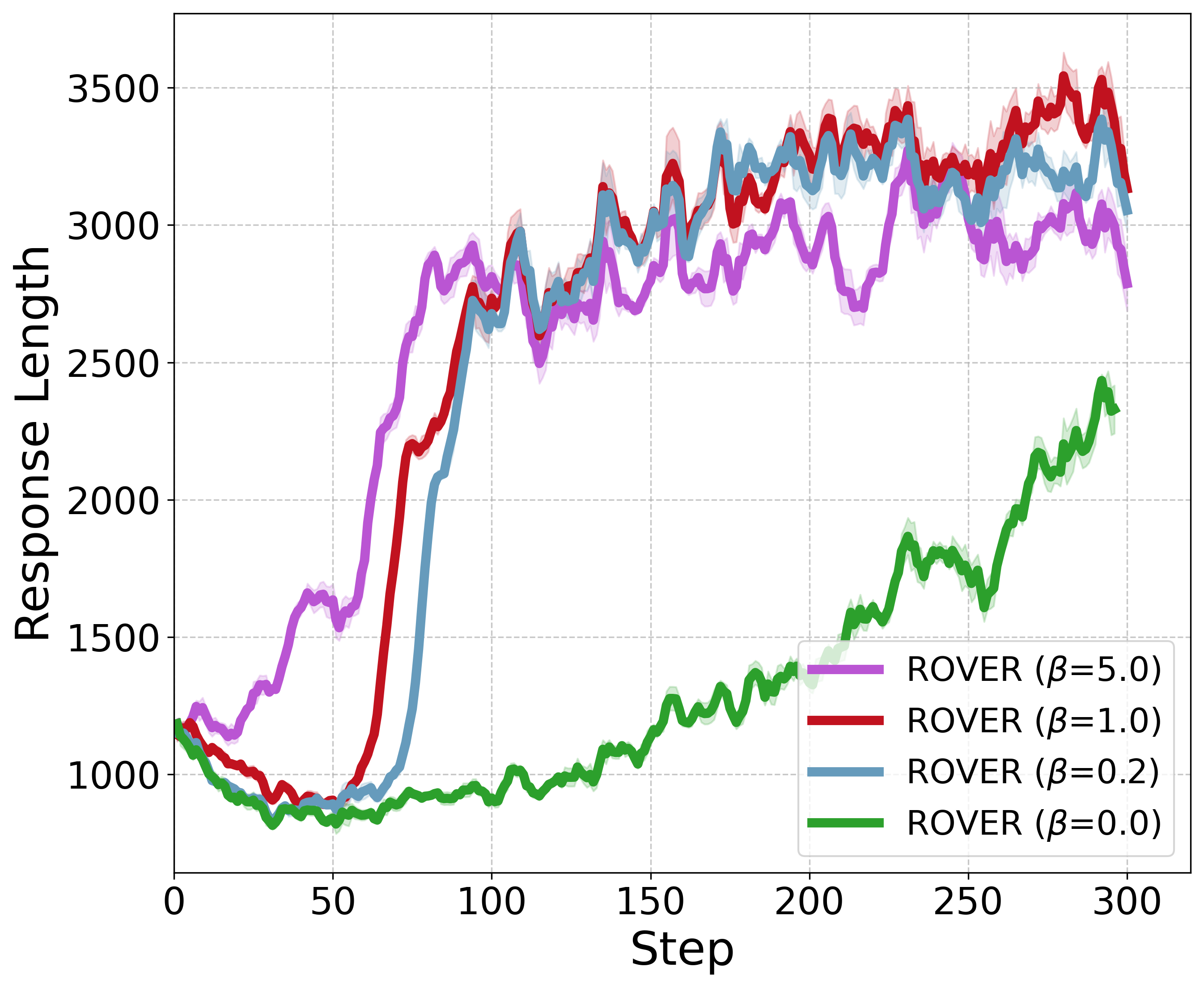
- Credit assignment: Determining which actions or tokens are responsible for observed outcomes. "to ensure efficient credit assignment, especially for long reasoning chains, we broadcast this centered reward to every token in the generation"
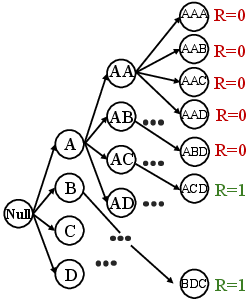
- Deterministic transitions: State transitions that are fully determined by the current state and action. "deterministic state transitions, tree-structured dynamics, and binary terminal rewards."
- Discount factor: A parameter (γ) controlling how future rewards are weighted relative to immediate rewards. "We set the discount factor γ=1 in practice."
- Diversity collapse: Loss of variability in generated outputs or explored actions during training. "they often suffer from training instability and diversity collapse"
- Entropy collapse: Reduction of policy entropy (randomness) during training, hindering exploration. "they suffer from unstable learning dynamics and entropy collapse induced by the reward-maximizing nature within the iterative policy evaluation-improvement cycle."
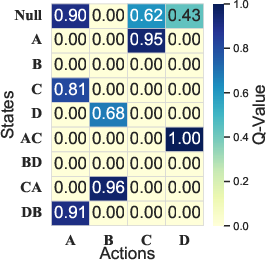
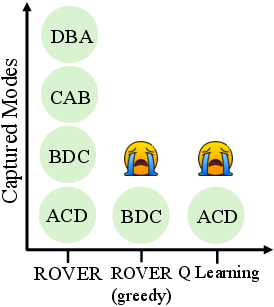
- ε-greedy exploration: A strategy that mostly chooses the best-known action but occasionally samples random actions to explore. "According to the Q-values, standard Q-learning with ε-greedy exploration converges to the mode ACD."
- Generalized BeLLMan update: A value update rule that replaces the max operator with a chosen aggregation operator (e.g., mean). "The corresponding Q-value for πu can be estimated using the generalized BeLLMan update"
- Generalized Policy Iteration (GPI): The alternating process of policy evaluation and policy improvement underlying many RL algorithms. "GPI~\citep{sutton1998reinforcement} is a unifying view that describes many RL algorithms (e.g., PPO) as illustrated in Fig.~\ref{fig:gpi}."
- Group-Relative Policy Optimization (GRPO): A policy optimization method that normalizes rewards within sampled groups to reduce variance. "specialized derivatives like Group-Relative Policy Optimization (GRPO)"
- Group reward centering: Subtracting the group mean reward from individual rewards to reduce variance and stabilize learning. "we leverage group reward centering inspired by \citet{naik2024reward}"
- Importance sampling ratio: The likelihood ratio used to correct for differences between the current policy and the behavior policy. "where ${\rm IS}_t={\pi_{\theta}(a_t|s_t)}/{\pi_{\theta_{\rm old}(a_t|s_t)}$ is the importance sampling ratio,"
- KL regularization: Penalizing divergence from a reference policy to stabilize training and maintain exploration. "KL regularization~\citep{liu2025prorl}"
- KL-divergence penalty: A regularization term that discourages large deviations from a reference distribution. "rely on a KL-divergence penalty () to prevent catastrophic forgetting and maintain exploration during continual learning"
- Markov Decision Process (MDP): A formal framework for sequential decision-making with states, actions, rewards, and transitions. "We formulate the problem as a Markov Decision Process (MDP), defined by a tuple ."
- Mean operator: An aggregation that averages action values, here used to evaluate a uniform policy. "The mean operator corresponds to evaluating a uniform policy"
- Mode collapse: Converging to a single solution or pathway despite multiple valid options. "this deterministic approach often leads to mode collapse and sacrifices diversity"
- Off-policy corrections: Adjustments in learning to account for data collected under a different policy than the one being optimized. "without off-policy corrections or the implementation complexity of popular methods like PPO and GRPO."
- Out-of-distribution (O.O.D): Data or tasks that differ significantly from the distribution seen during training. "along with the O.O.D benchmark GPQA-diamond"
- Pass@k: The probability of producing at least one correct solution within k sampled attempts. "We report pass@1 and pass@ for comprehensive analysis, where pass@ measures diversity and the reasoning boundary"
- Policy entropy: A measure of randomness in action selection; higher entropy supports exploration. "two GRPO variants designed for policy entropy preservation"
- Policy evaluation: Estimating how good a policy is (e.g., via value/Q-functions) without changing it. "our proposed method relies solely on policy evaluation to derive the Q-values of a fixed, uniform random policy"
- Policy improvement: Updating a policy to favor actions with higher estimated value. "policy improvement that updates the policy to prefer actions scored better by the current estimates"
- Proximal Policy Optimization (PPO): A widely used on-policy RL algorithm employing clipped objectives for stable updates. "Proximal Policy Optimization (PPO), a powerful algorithm originally designed for standard deep RL benchmarks"
- Q-function: The expected return from a state-action pair under a given policy. "the optimal action can be recovered from the Q-function of a fixed uniformly random policy"
- Q-learning: An off-policy RL algorithm that learns action values via bootstrapped updates and greedy improvement. "According to the Q-values, standard Q-learning with ε-greedy exploration converges to the mode ACD."
- Softmax: A function converting values into a probability distribution that emphasizes larger inputs. "samples actions from a softmax over these uniform-policy Q-values."
- Temperature parameter: A scaling factor in softmax sampling that controls the trade-off between exploration and exploitation. "where is a temperature parameter."
- Tree-structured state space: A state space where each state has a unique parent and actions lead to disjoint subtrees. "tree-structured state space"
- Uniform random policy: A policy that selects among available actions uniformly at random. "the uniform random policy "
- Value network: A model that estimates state or action values to guide policy learning. "which eliminates the need for a separate value network"
- Verifiable rewards: Rewards determinable by an external checker (e.g., mathematical correctness). "reinforcement learning (RL) for post-training LLMs with verifiable rewards, such as mathematical reasoning tasks."
Collections
Sign up for free to add this paper to one or more collections.