SLA: Beyond Sparsity in Diffusion Transformers via Fine-Tunable Sparse-Linear Attention (2509.24006v1)

Abstract: In Diffusion Transformer (DiT) models, particularly for video generation, attention latency is a major bottleneck due to the long sequence length and the quadratic complexity. We find that attention weights can be separated into two parts: a small fraction of large weights with high rank and the remaining weights with very low rank. This naturally suggests applying sparse acceleration to the first part and low-rank acceleration to the second. Based on this finding, we propose SLA (Sparse-Linear Attention), a trainable attention method that fuses sparse and linear attention to accelerate diffusion models. SLA classifies attention weights into critical, marginal, and negligible categories, applying O(N^2) attention to critical weights, O(N) attention to marginal weights, and skipping negligible ones. SLA combines these computations into a single GPU kernel and supports both forward and backward passes. With only a few fine-tuning steps using SLA, DiT models achieve a 20x reduction in attention computation, resulting in significant acceleration without loss of generation quality. Experiments show that SLA reduces attention computation by 95% without degrading end-to-end generation quality, outperforming baseline methods. In addition, we implement an efficient GPU kernel for SLA, which yields a 13.7x speedup in attention computation and a 2.2x end-to-end speedup in video generation on Wan2.1-1.3B.

• The paper introduces SLA, a mechanism that combines block-sparse and linear attention to cut computation by 95% without quality loss.
• It partitions attention weights into critical, marginal, and negligible groups, achieving 13.7× kernel and 2.2× end-to-end speedups.
• The method leverages fused GPU kernels and dynamic block partitioning, making it practical for large-scale video and image diffusion models.

SLA: Fine-Tunable Sparse-Linear Attention for Efficient Diffusion Transformers

Introduction and Motivation

Diffusion Transformers (DiTs) have become the de facto architecture for high-fidelity video and image generation, but their scalability is fundamentally constrained by the quadratic complexity of the attention mechanism, especially as sequence lengths reach tens or hundreds of thousands. Existing approaches to efficient attention fall into two categories: sparse attention, which masks out most attention scores, and linear attention, which reformulates the computation to achieve $\mathcal{O}(N)$ complexity. However, both approaches have critical limitations in the context of video diffusion: linear attention alone leads to severe quality degradation, while sparse attention cannot achieve high enough sparsity without significant loss in fidelity.

A key empirical observation in this work is that attention weights in DiTs are highly skewed: a small fraction of weights are large and high-rank, while the vast majority are extremely small and low-rank. This motivates a hybrid approach that applies full (sparse) attention to the critical weights and linear attention to the marginal ones, skipping the negligible entries entirely.

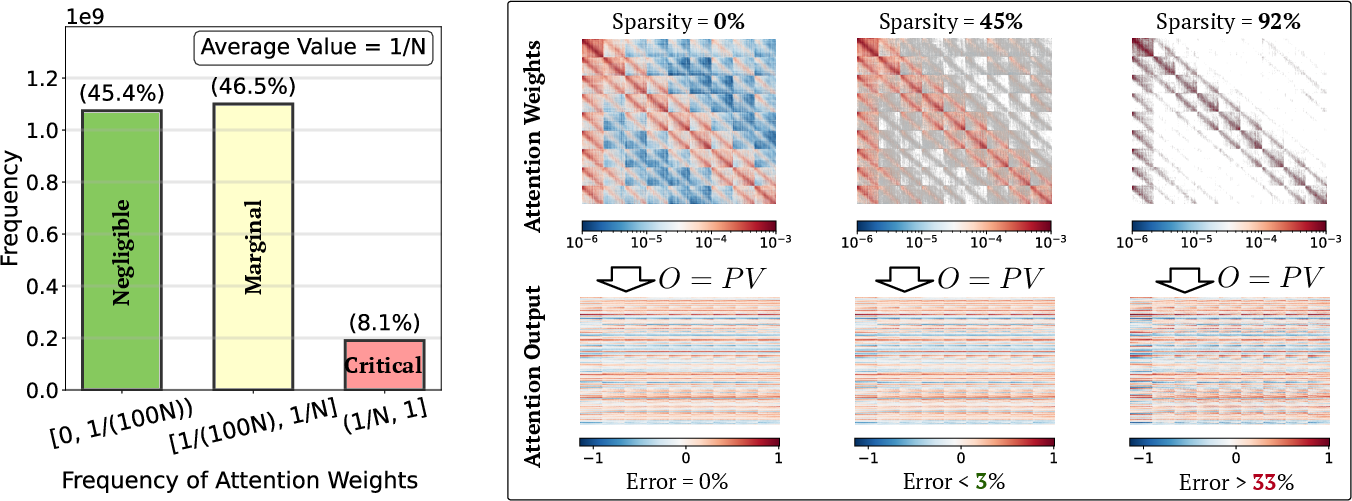
Figure 1: The left figure shows a typical distribution of attention weights sampled from the Wan2.1 model. The right figure shows the accuracy of sparse attention with different sparsity.

SLA: Sparse-Linear Attention Mechanism

SLA (Sparse-Linear Attention) is a trainable hybrid attention mechanism that partitions the attention weight matrix into three categories:

• Critical: Top $k_h\%$ of attention blocks, computed exactly using block-sparse FlashAttention.
• Marginal: Middle $k_m\%$ of blocks, approximated using linear attention.
• Negligible: Bottom $k_l\%$ of blocks, skipped entirely.

This partitioning is performed dynamically using a compressed attention matrix $P_c$ obtained via mean pooling and softmax over block representations. The mask $M_c$ encodes the assignment of each block to one of the three categories.

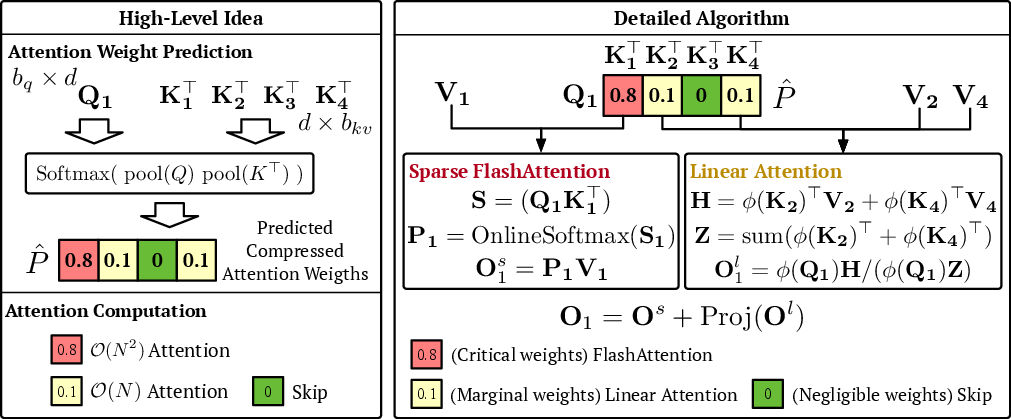
Figure 2: Overview of SLA. The left figure illustrates the high-level idea: attention weights are classified into three categories and assigned to computations of different complexity. The right figure shows the detailed forward algorithm of SLA using the predicted compressed attention weights.

Sparse and Linear Components

• Sparse Attention: For blocks marked as critical, standard block-sparse attention is computed using FlashAttention, ensuring high-rank structure is preserved where it matters most.
• Linear Attention: For marginal blocks, a linear attention variant is applied, leveraging the low-rank structure of these entries. The output is projected via a learnable linear transformation to mitigate distribution mismatch.
• Fusion: The outputs of the sparse and linear components are summed, with the linear component acting as a learnable compensation rather than a direct approximation.

This design enables SLA to achieve extremely high sparsity (up to 95%) while maintaining generation quality, as the computationally expensive $\mathcal{O}(N^2)$ operations are reserved only for the most important attention blocks.

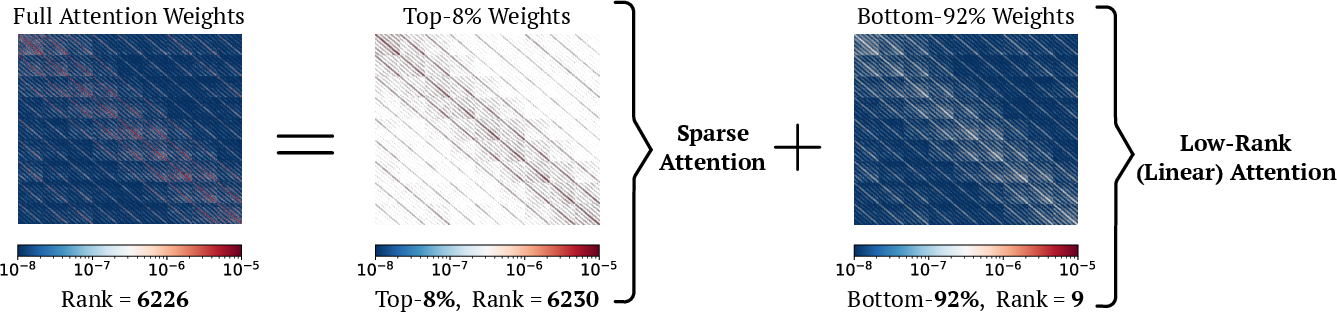
Figure 3: Decomposition of attention weights. The left shows the full weights, the middle the top 8%, and the right the bottom 92% (low-rank structure).

Implementation and Optimization

SLA is implemented as a fused GPU kernel supporting both forward and backward passes, with several optimizations:

• Lookup Tables: For high sparsity, nonzero block indices are precomputed to minimize memory access overhead.
• Pre-aggregation: For linear attention, row/column sums are precomputed to reduce redundant additions.
• Method of Four Russians: For intermediate sparsity, subset sums are precomputed for efficient block aggregation.

The forward pass involves block-wise computation of sparse and linear attention, with precomputation of intermediate results for the linear component. The backward pass fuses gradient computation for both components, following the chain rule and leveraging block structure for efficiency.

Empirical Results

SLA is evaluated on the Wan2.1-1.3B video diffusion model and LightningDiT for image generation. Key results include:

• Attention Computation Reduction: SLA achieves a 95% reduction in attention computation (FLOPs) at 95% sparsity, with no degradation in video or image quality.
• Kernel and End-to-End Speedup: SLA delivers a 13.7× speedup in the attention kernel and a 2.2× end-to-end speedup in video generation latency on RTX5090 GPUs.
• Quality Preservation: SLA matches or exceeds the quality of full attention and outperforms all sparse and linear baselines, even at much higher sparsity.

  Figure 4: Video generation examples on Wan2.1 fine-tuned with full attention, linear attention, sparse attention, and SLA. SLA achieves 95% sparsity with lossless video quality.

  

  Figure 5: Video examples using Wan2.1 fine-tuned with SLA and baselines. Only SLA and full attention produce high-quality, temporally consistent videos.

  

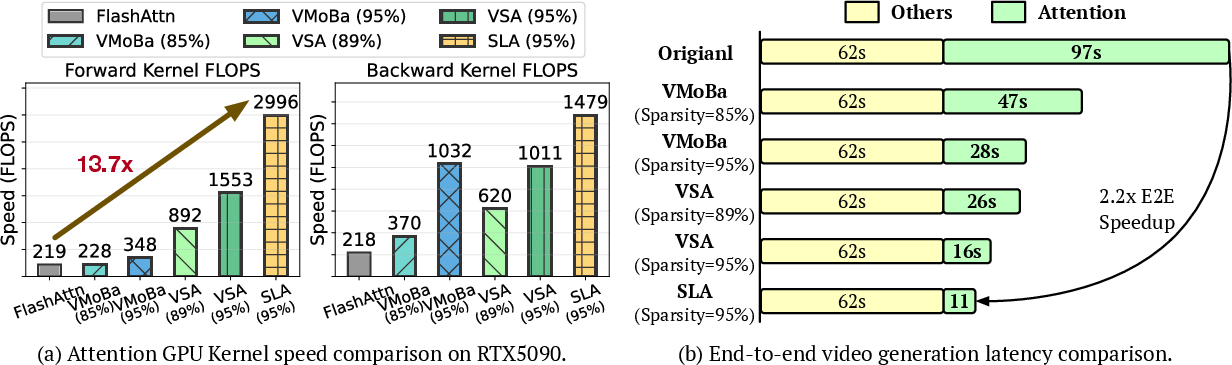
  Figure 6: Attention kernel speed and end-to-end generation latency of SLA and baselines on Wan2.1-1.3B with RTX5090.

Ablation studies confirm that neither sparse nor linear attention alone can achieve the same trade-off between efficiency and quality. The fusion strategy and the use of softmax as the activation function in the linear component are both critical for optimal performance.

Theoretical and Practical Implications

The decomposition of attention weights into high-rank and low-rank components provides a principled explanation for the failure of pure linear or sparse attention in high-fidelity generative models. SLA's hybrid approach leverages this structure, enabling aggressive sparsification without sacrificing expressivity or quality.

Practically, SLA enables the deployment of large-scale video and image diffusion models on commodity hardware, reducing both inference and fine-tuning costs. The method is compatible with existing DiT architectures and requires only a few thousand fine-tuning steps to adapt pretrained models.

Theoretically, this work suggests that future efficient attention mechanisms should exploit the heterogeneous structure of attention weights, rather than relying on uniform approximations. The block-wise, dynamic partitioning strategy of SLA is likely to be extensible to other domains, including long-context LLMing and multimodal generative models.

Future Directions

Potential avenues for further research include:

• Adaptive Block Partitioning: Learning or dynamically adjusting block sizes and thresholds for critical/marginal/negotiable categories.
• Integration with Quantization: Combining SLA with low-precision attention kernels for further efficiency gains.
• Application to Other Modalities: Extending SLA to long-context LLMs, audio, and multimodal transformers.
• Theoretical Analysis: Formalizing the relationship between attention weight distribution, rank, and generative quality.

Conclusion

SLA introduces a fine-tunable, hybrid sparse-linear attention mechanism that achieves substantial acceleration of diffusion transformers without compromising generation quality. By partitioning attention computation according to empirical importance and leveraging both sparse and linear approximations, SLA sets a new standard for efficient, scalable generative modeling in high-dimensional domains.