Taxonomy-aware Dynamic Motion Generation on Hyperbolic Manifolds (2509.21281v1)

Abstract: Human-like motion generation for robots often draws inspiration from biomechanical studies, which often categorize complex human motions into hierarchical taxonomies. While these taxonomies provide rich structural information about how movements relate to one another, this information is frequently overlooked in motion generation models, leading to a disconnect between the generated motions and their underlying hierarchical structure. This paper introduces the \ac{gphdm}, a novel approach that learns latent representations preserving both the hierarchical structure of motions and their temporal dynamics to ensure physical consistency. Our model achieves this by extending the dynamics prior of the Gaussian Process Dynamical Model (GPDM) to the hyperbolic manifold and integrating it with taxonomy-aware inductive biases. Building on this geometry- and taxonomy-aware frameworks, we propose three novel mechanisms for generating motions that are both taxonomically-structured and physically-consistent: two probabilistic recursive approaches and a method based on pullback-metric geodesics. Experiments on generating realistic motion sequences on the hand grasping taxonomy show that the proposed GPHDM faithfully encodes the underlying taxonomy and temporal dynamics, and generates novel physically-consistent trajectories.

• The paper presents GPHDM, a model extending GPDM to hyperbolic manifolds to generate taxonomy-aware, physically consistent motions.
• It integrates a hyperbolic dynamics prior with a taxonomy regularization loss using Riemannian optimization to preserve hierarchical structure.
• Empirical results show GPHDM achieves smoother latent trajectories and lower mean squared jerk on human hand grasp motions compared to Euclidean baselines.

Taxonomy-aware Dynamic Motion Generation on Hyperbolic Manifolds

Introduction and Motivation

The paper introduces the Gaussian Process Hyperbolic Dynamical Model (GPHDM), a probabilistic latent variable model designed to generate physically consistent, taxonomy-aware motion trajectories by leveraging hyperbolic geometry. The motivation stems from the observation that many human motion taxonomies—such as hand grasp types—are inherently hierarchical and tree-structured. Traditional motion generation models, particularly those based on Euclidean latent spaces, fail to explicitly encode this hierarchical structure, leading to generated motions that may not respect the taxonomy or exhibit physically implausible transitions.

The GPHDM extends the Gaussian Process Dynamical Model (GPDM) to hyperbolic manifolds, integrating taxonomy-aware inductive biases and temporal dynamics. This approach enables the generation of novel motion sequences that are both consistent with the underlying taxonomy and physically plausible.

Background: Hyperbolic Geometry and Latent Variable Models

Hyperbolic manifolds, characterized by constant negative curvature, are well-suited for embedding tree-like structures due to their exponential volume growth and ability to represent hierarchical relationships with low distortion. The Lorentz and Poincaré models are commonly used representations, with the Lorentz model preferred here for numerical stability.

The Gaussian Process Latent Variable Model (GPLVM) provides a probabilistic mapping from a low-dimensional latent space to high-dimensional observations. The GPDM augments the GPLVM with a temporal dynamics prior, encouraging smooth latent trajectories. The Gaussian Process Hyperbolic Latent Variable Model (GPHLVM) further adapts this framework to hyperbolic spaces, enabling the preservation of hierarchical relationships in the latent space.

However, prior work with GPHLVMs demonstrated that while taxonomy structure can be preserved, generated motions along latent geodesics often traverse data-sparse regions, resulting in physically implausible or high-uncertainty predictions.

The Gaussian Process Hyperbolic Dynamical Model (GPHDM)

The GPHDM addresses the limitations of previous models by introducing a hyperbolic dynamics prior that enforces temporal consistency in the latent space. The model is defined as follows:

• Latent Variables: $\bm{x}_t \in \mathbb{H}^{D_x}$, where $\mathbb{H}^{D_x}$ is a $D_x$-dimensional hyperbolic space.
• Observation Model: A GP maps latent variables to high-dimensional observations, with a hyperbolic kernel capturing the geometry.
• Dynamics Prior: A first-order Markov process in the hyperbolic space, with transitions modeled as wrapped Gaussians in the tangent space at each latent point.
• Taxonomy Regularization: A stress loss penalizes discrepancies between taxonomy graph distances and hyperbolic geodesic distances among latent variables, anchoring start and end points of trajectories to taxonomy nodes.

The model is trained via Riemannian optimization (Riemannian Adam), jointly optimizing latent variables and hyperparameters to maximize the posterior likelihood, balancing reconstruction, dynamics, and taxonomy preservation.

Motion Generation Mechanisms

The paper proposes three strategies for generating new motion trajectories in the hyperbolic latent space:

1. Recursive Mean Prediction: Sequentially predicts the next latent point by maximizing the likelihood under the hyperbolic dynamics prior. This approach is analogous to mean prediction in Euclidean GPDMs but requires Riemannian optimization due to the lack of closed-form solutions for the mean of wrapped Gaussian distributions on manifolds.
2. Conditional Optimization: Allows specification of start, goal, and intermediate points, optimizing the full conditional distribution of the latent trajectory under the dynamics prior. This enables interpolation between arbitrary taxonomy nodes but is subject to the directionality imposed by the Markov prior.
3. Pullback-metric Geodesics: Computes geodesics with respect to the pullback metric induced by the GP mapping, rather than the intrinsic hyperbolic metric. This confines generated trajectories to regions of high data density, reducing uncertainty and improving physical plausibility.

Empirical Evaluation

The GPHDM is evaluated on a dataset of human hand grasp motions, structured according to a hierarchical taxonomy. The experiments compare Euclidean and hyperbolic variants of GPLVM and GPDM, with and without dynamics priors, in both 2D and 3D latent spaces.

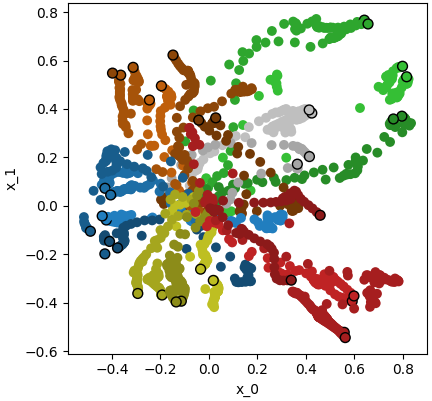
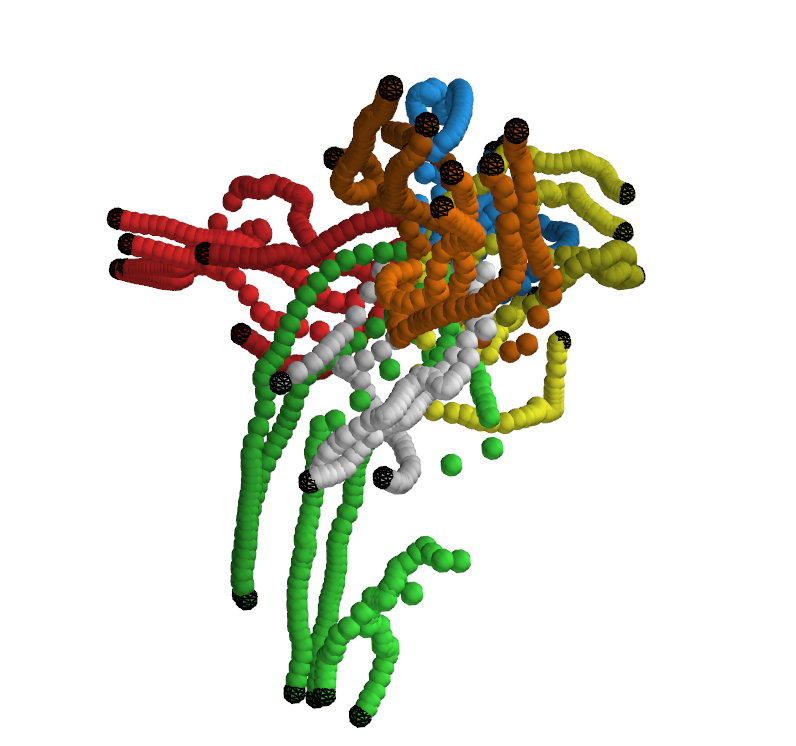
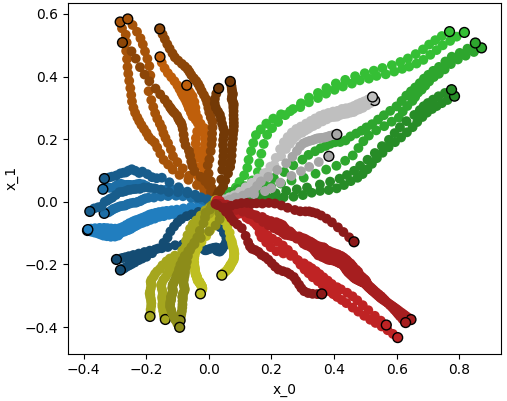
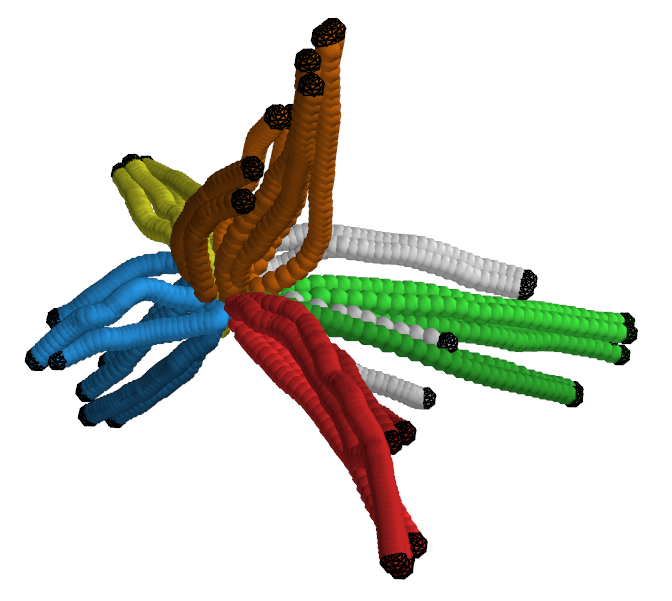
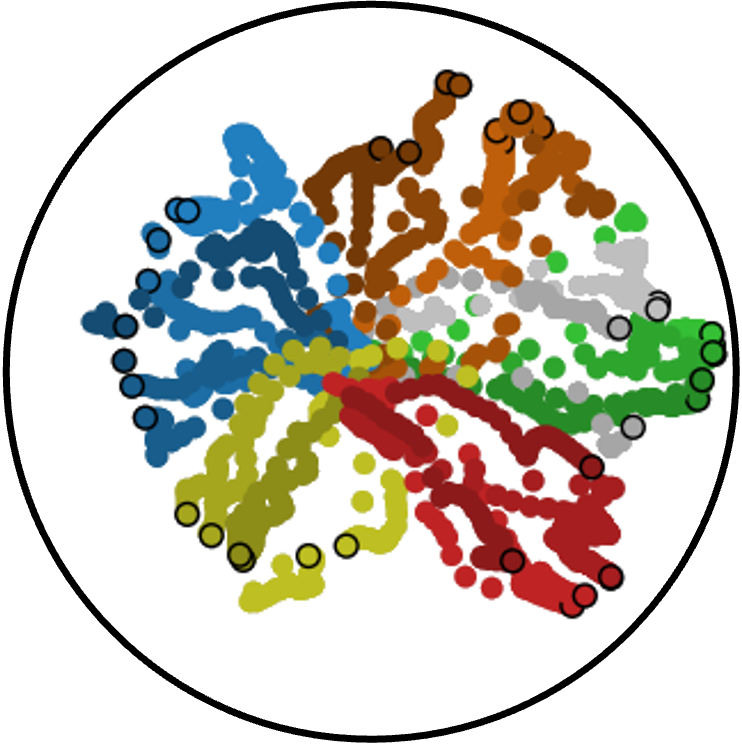
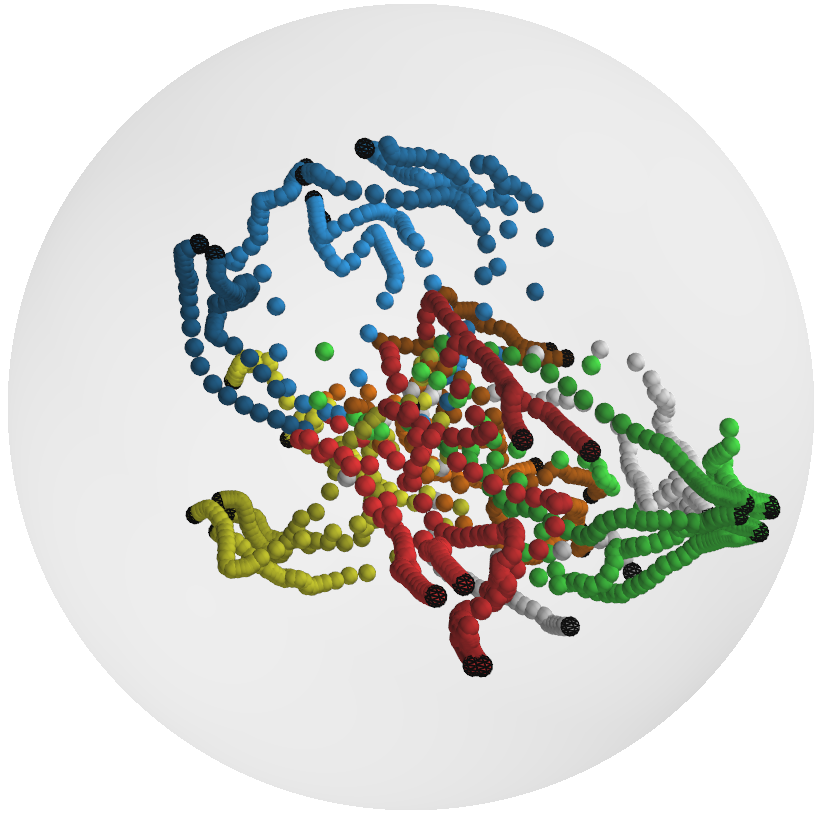
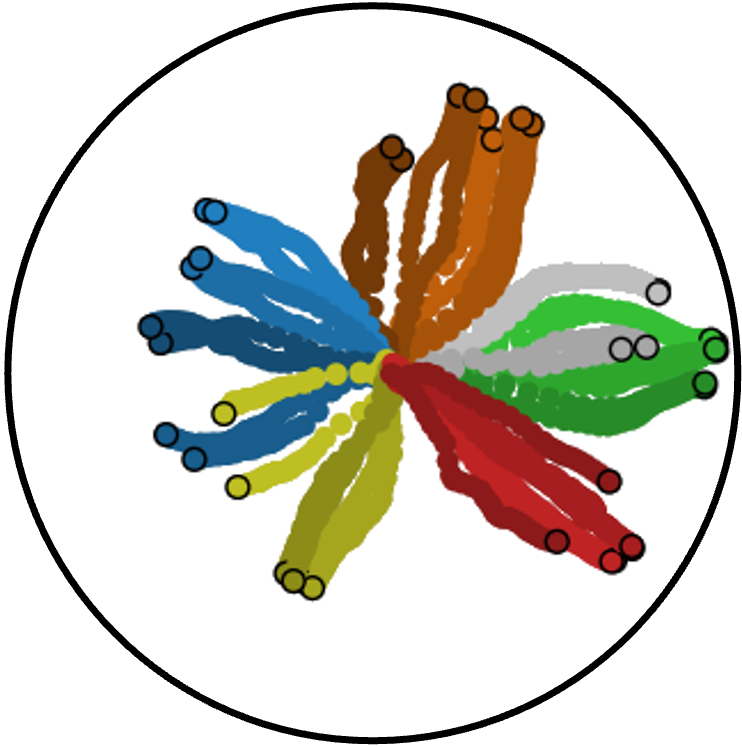
Figure 1: Embeddings of hand grasps in 2D and 3D latent spaces for GPLVM, GPDM, GPHLVM, and GPHDM, colored by grasp class.

The results demonstrate that:

• Hyperbolic models (GPHLVM, GPHDM) more accurately preserve the taxonomy structure, especially in low-dimensional latent spaces.
• Dynamics priors (GPDM, GPHDM) yield significantly smoother latent trajectories, as quantified by mean squared jerk (MSJ).
• The GPHDM achieves the lowest MSJ and best taxonomy preservation in 3D, indicating effective integration of hierarchical and temporal structure.

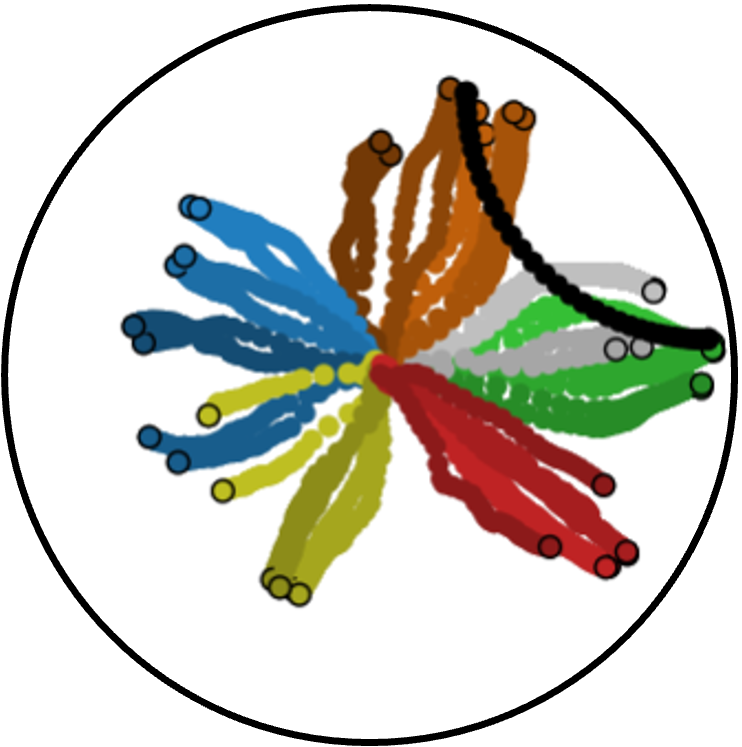
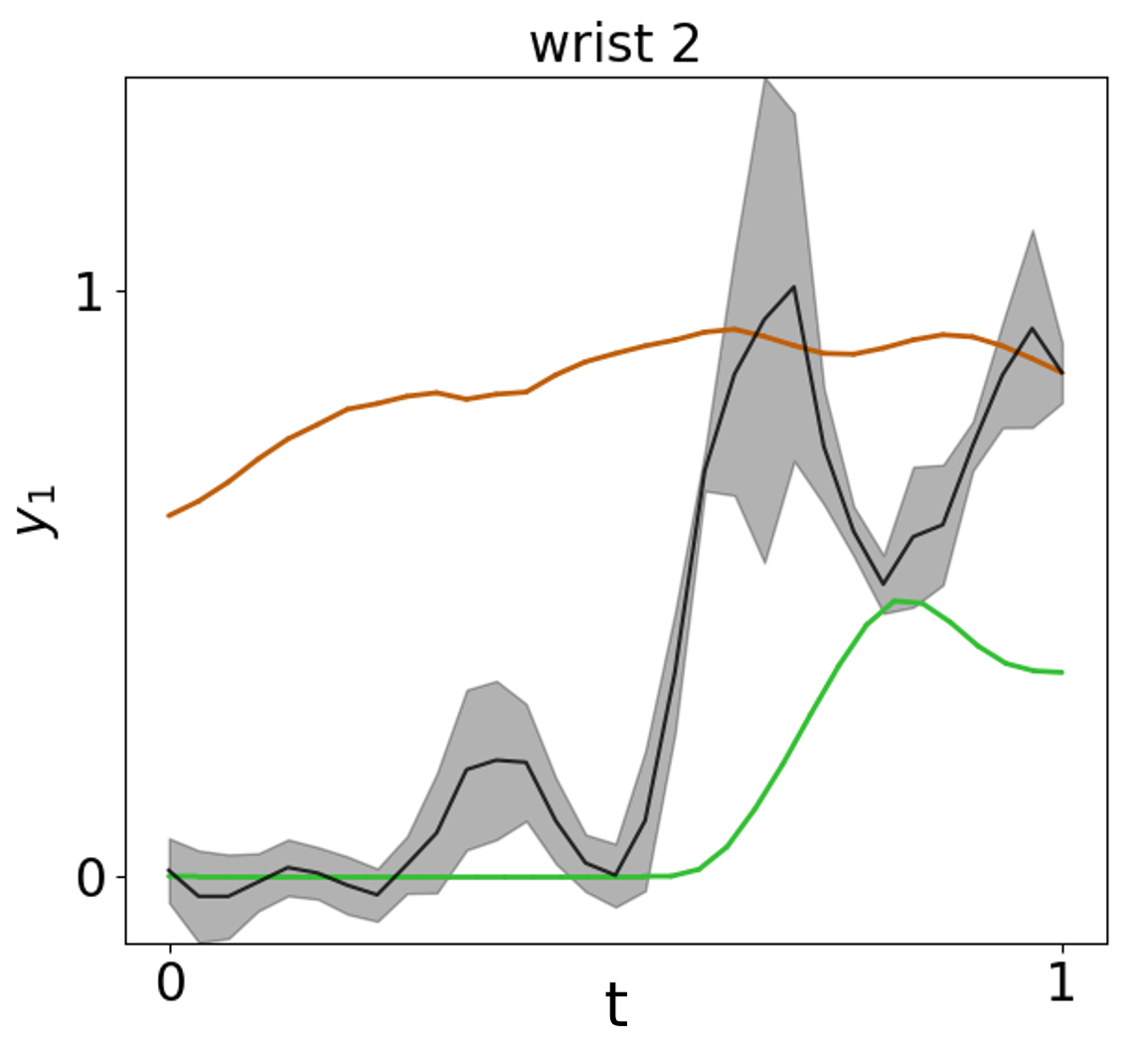
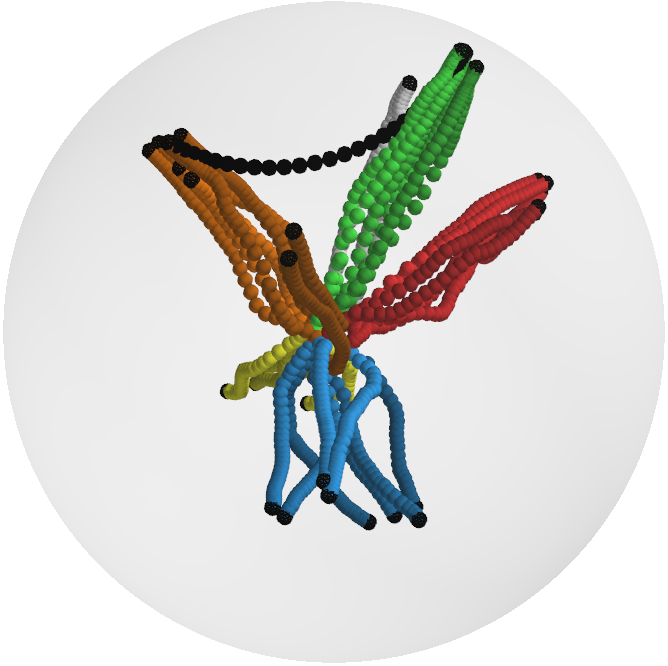
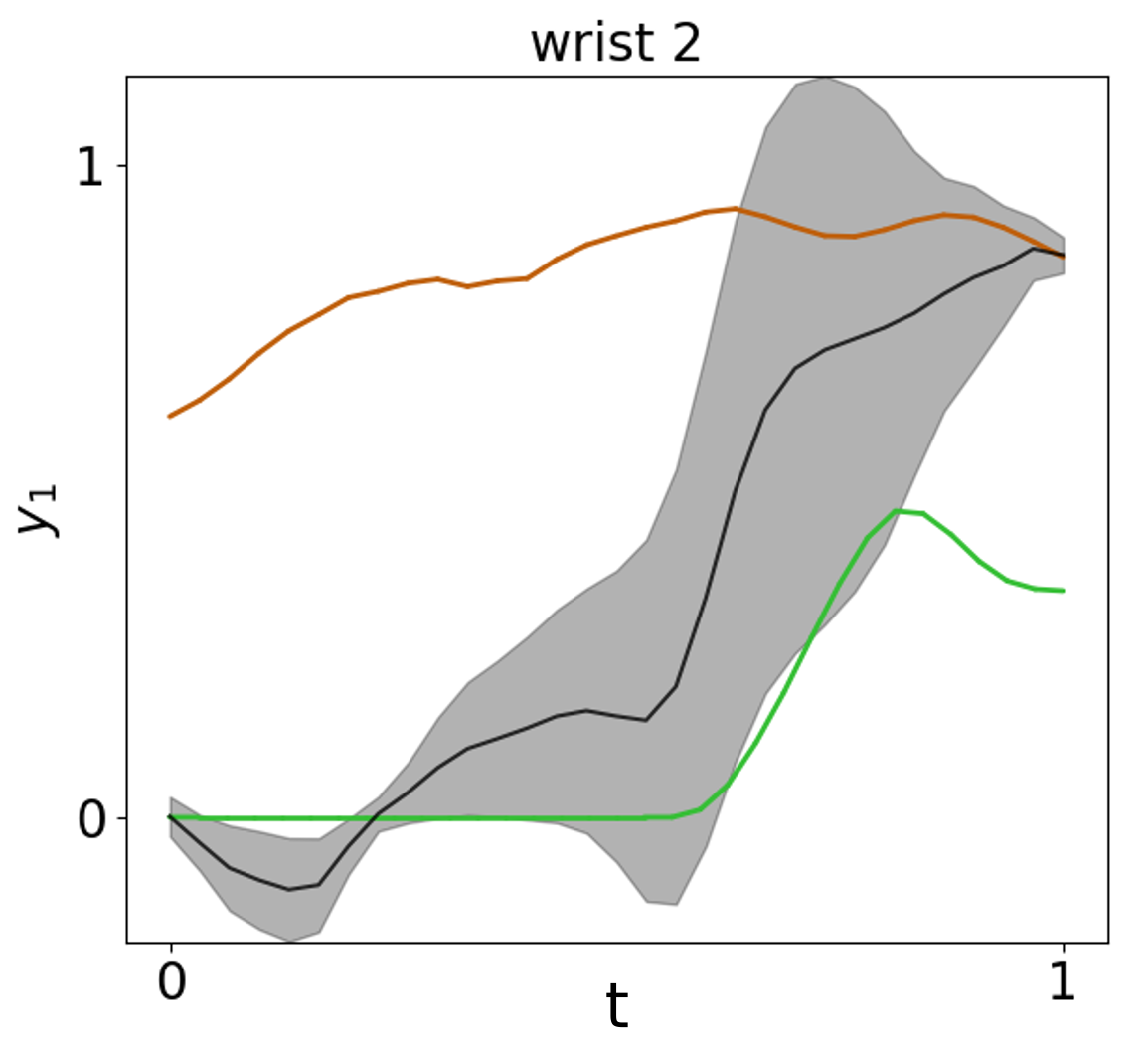
Figure 2: Left: Hyperbolic geodesics between grasp classes in latent space. Right: Decoded motion predictions along geodesics, with uncertainty bands and training trajectories.

The analysis of motion generation strategies reveals that:

• Hyperbolic geodesics between taxonomy nodes often traverse data-sparse regions, resulting in high-uncertainty, physically implausible motions.
• Recursive and conditional predictions follow the learned dynamics but may be limited by the directionality of the Markov prior and can still enter low-density regions.
• Pullback-metric geodesics closely adhere to the data manifold, producing low-uncertainty, physically consistent motions that respect both taxonomy and dynamics.

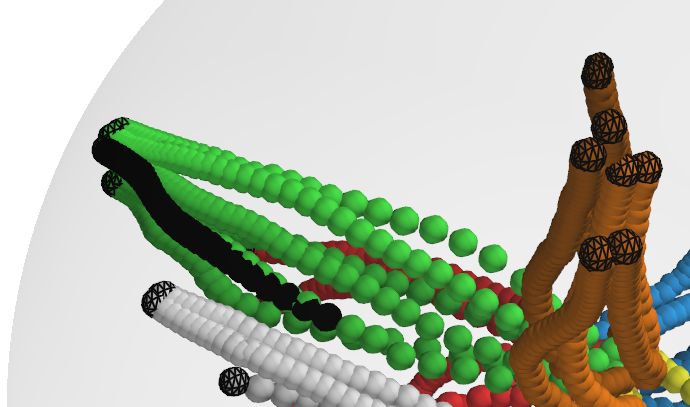
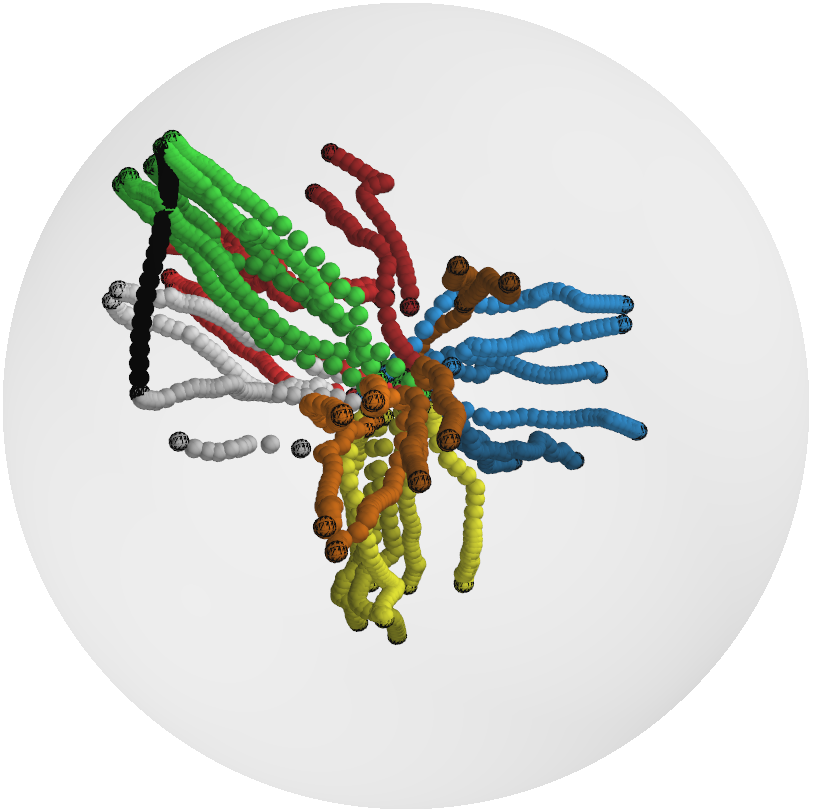
Figure 3: Latent trajectories generated via recursive motion generation in 3D GPHDM.

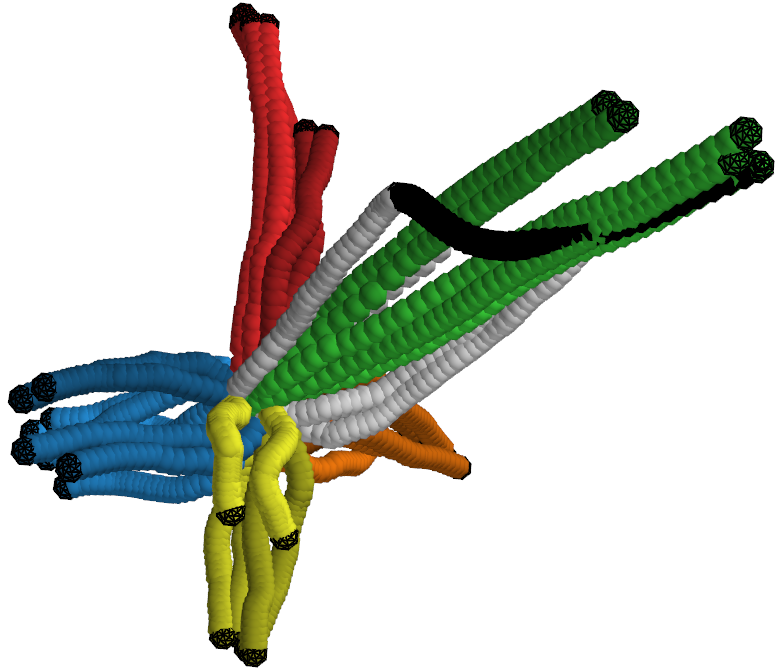
Figure 4: Illustration of directionality induced by the GPDM's Markov prior in conditional predictions.

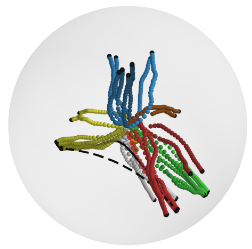
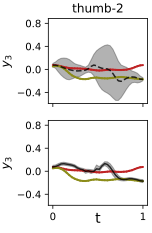
Figure 5: Top left: 3D embeddings with hyperbolic and pullback geodesics from ring to spherical grasp. Top right: Decoded motion predictions. Bottom: Generated hand motions from decoded geodesics.

Implications and Future Directions

The GPHDM framework demonstrates that integrating hyperbolic geometry, taxonomy-aware regularization, and temporal dynamics yields latent spaces that are both structurally faithful and dynamically consistent. The use of pullback-metric geodesics for motion generation is particularly effective in producing physically plausible, low-uncertainty trajectories.

This approach has direct implications for robotics, where generating human-like, taxonomy-consistent motions is critical for dexterous manipulation and safe human-robot interaction. The methodology is extensible to other domains with hierarchical structure, such as full-body pose generation, manipulation primitives, and even non-robotic hierarchical data.

Future research directions include:

• Scaling to larger, more complex taxonomies and higher-dimensional motion data.
• Incorporating richer dynamics models (e.g., higher-order Markov processes, control inputs).
• Extending to mixed-curvature or product manifolds for representing more general hierarchical and non-hierarchical relationships.
• Integrating with reinforcement learning or imitation learning frameworks for end-to-end policy learning on structured manifolds.

Conclusion

The GPHDM provides a principled, geometry-aware framework for dynamic motion generation that respects both the hierarchical structure of motion taxonomies and the temporal consistency of physical trajectories. The combination of hyperbolic latent spaces, dynamics priors, and pullback-metric geodesics enables the synthesis of novel, physically consistent motions that are aligned with human-designed taxonomies, with clear benefits for robotics and structured generative modeling.