Geometric Autoencoder Priors for Bayesian Inversion: Learn First Observe Later (2509.19929v1)

Abstract: Uncertainty Quantification (UQ) is paramount for inference in engineering applications. A common inference task is to recover full-field information of physical systems from a small number of noisy observations, a usually highly ill-posed problem. Critically, engineering systems often have complicated and variable geometries prohibiting the use of standard Bayesian UQ. In this work, we introduce Geometric Autoencoders for Bayesian Inversion (GABI), a framework for learning geometry-aware generative models of physical responses that serve as highly informative geometry-conditioned priors for Bayesian inversion. Following a ''learn first, observe later'' paradigm, GABI distills information from large datasets of systems with varying geometries, without requiring knowledge of governing PDEs, boundary conditions, or observation processes, into a rich latent prior. At inference time, this prior is seamlessly combined with the likelihood of the specific observation process, yielding a geometry-adapted posterior distribution. Our proposed framework is architecture agnostic. A creative use of Approximate Bayesian Computation (ABC) sampling yields an efficient implementation that utilizes modern GPU hardware. We test our method on: steady-state heat over rectangular domains; Reynold-Averaged Navier-Stokes (RANS) flow around airfoils; Helmholtz resonance and source localization on 3D car bodies; RANS airflow over terrain. We find: the predictive accuracy to be comparable to deterministic supervised learning approaches in the restricted setting where supervised learning is applicable; UQ to be well calibrated and robust on challenging problems with complex geometries. The method provides a flexible geometry-aware train-once-use-anywhere foundation model which is independent of any particular observation process.

• The paper introduces the GABI framework, leveraging geometry-conditioned autoencoders to learn generative priors without requiring fixed observation processes.
• It employs ABC sampling and latent space pushforward inversion to accurately reconstruct full-field solutions and quantify uncertainty across diverse applications.
• The method outperforms Gaussian Process baselines and direct map approaches in tasks from steady-state heat problems to airfoil flow and car body acoustics.

Geometric Autoencoder Priors for Bayesian Inversion: Learn First Observe Later

Introduction and Motivation

This paper introduces the Geometric Autoencoder for Bayesian Inversion (GABI) framework, which addresses the challenge of Bayesian inversion in engineering systems with complex and variable geometries. The central problem is the recovery of full-field physical states from sparse, noisy observations—a highly ill-posed inverse problem, especially when the underlying geometry varies across instances. Traditional Bayesian approaches suffer from vague priors and poor posterior concentration in such settings, while supervised learning methods require the observation process to be fixed at training time, limiting their flexibility.

GABI proposes a "learn first, observe later" paradigm: a geometry-aware generative model is trained on a large dataset of full-field solutions over diverse geometries, without requiring knowledge of governing PDEs, boundary conditions, or observation processes. At inference, this learned prior is combined with the likelihood induced by the specific observation process, yielding a geometry-adapted posterior. The framework is architecture-agnostic and leverages Approximate Bayesian Computation (ABC) for efficient posterior sampling.

Methodological Framework

Geometry-Conditioned Generative Priors

GABI employs graph-based autoencoders to encode both geometry and physical fields into a latent space. The encoder $E^\theta_n$ maps a solution field on a geometry to a latent vector, while the decoder $D^\psi_n$ reconstructs the field from the latent vector and geometry. The autoencoder is trained to minimize reconstruction error and regularize the latent distribution (typically via MMD to a standard normal), resulting in a geometry-conditioned generative prior.

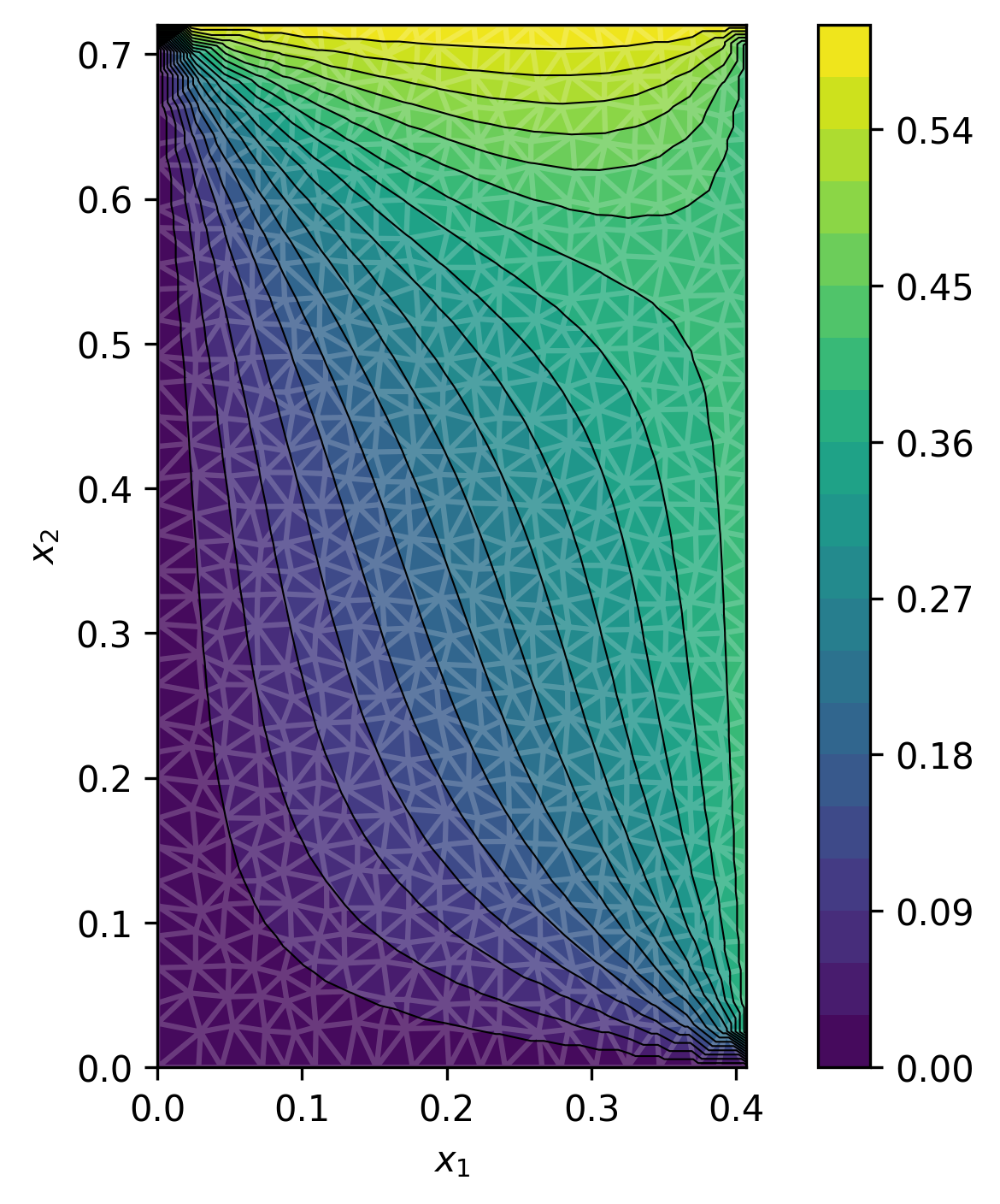
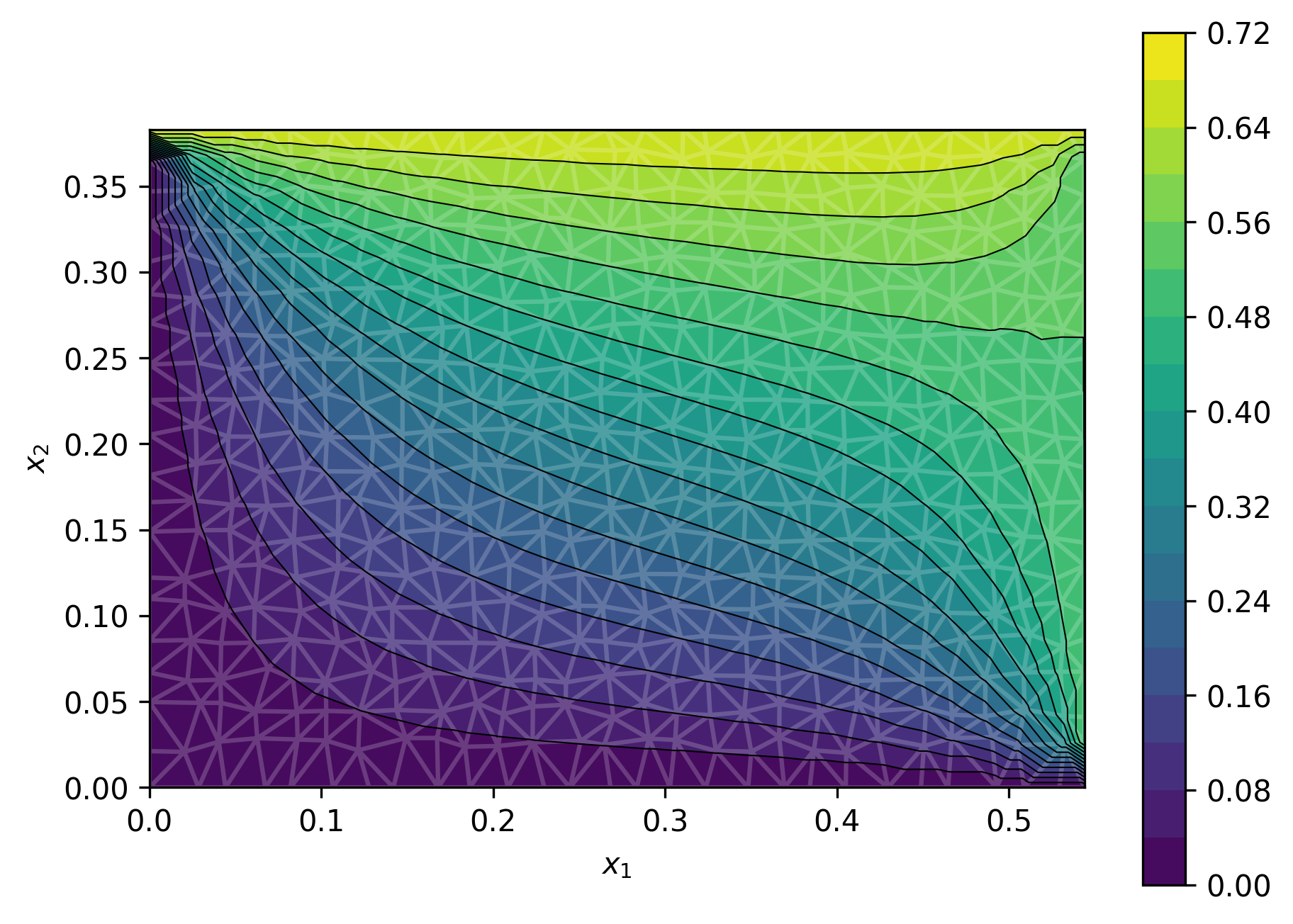
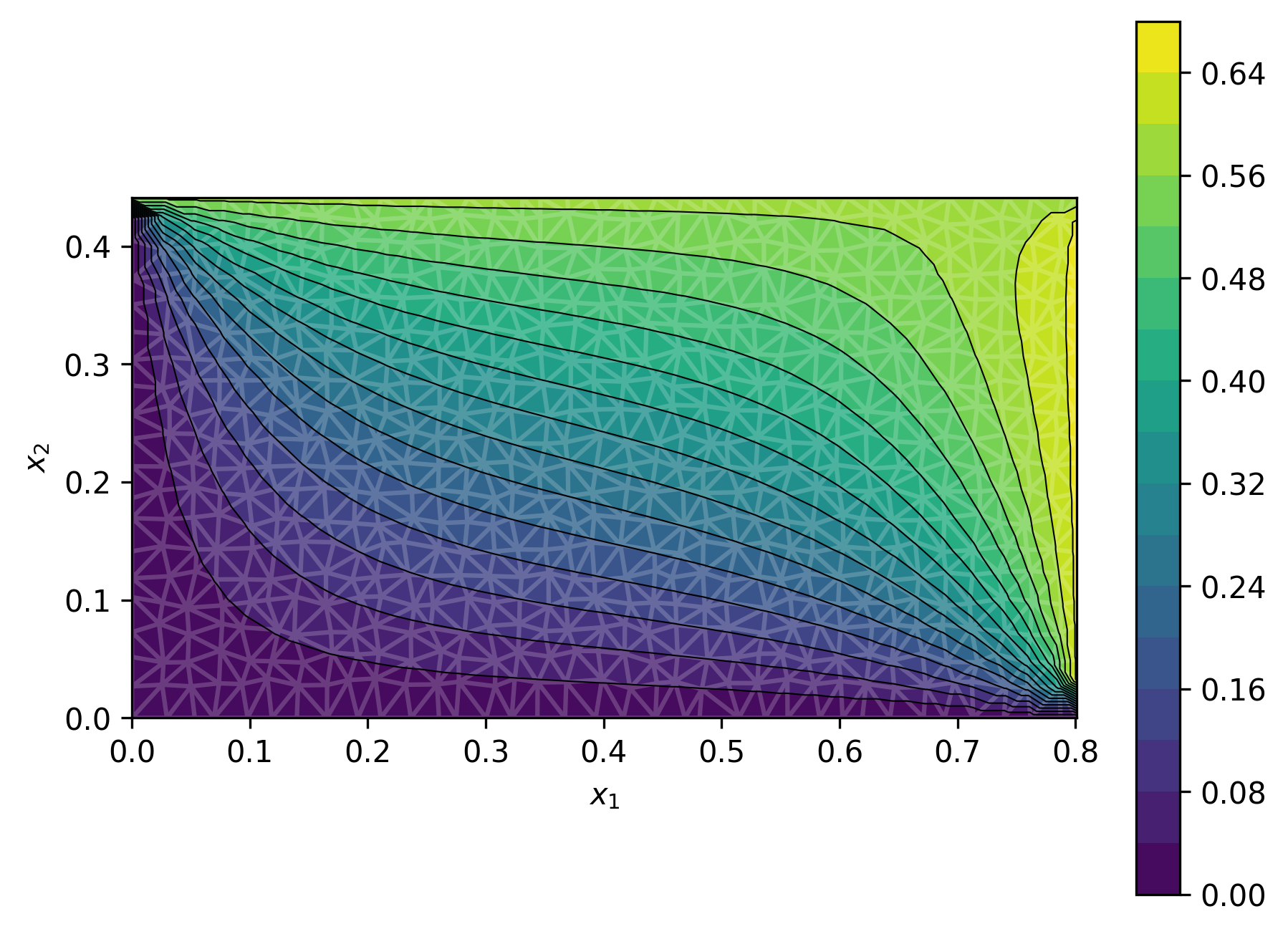
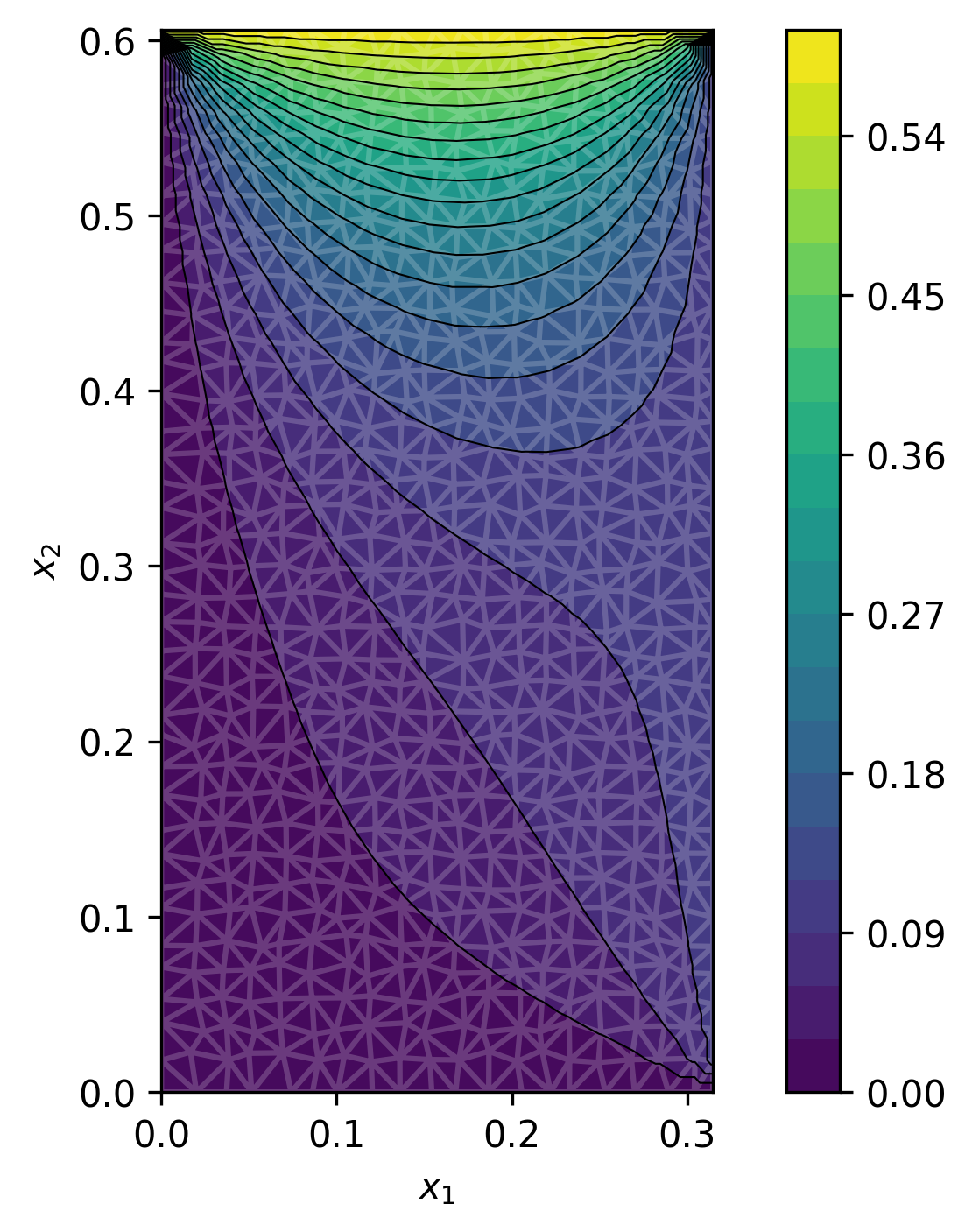
Figure 1: Four out of 1k geometries and solutions in dataset for the steady-state heat problem.

Bayesian Inversion via Pushforward Priors

The key theoretical result is the equivalence between Bayesian inversion with a pushforward prior and inversion in the latent space. Given a new geometry and sparse observations, the likelihood is defined in terms of the decoded latent variable. The posterior over the latent space is sampled (via ABC or MCMC), and decoded to yield posterior samples of the full-field solution.

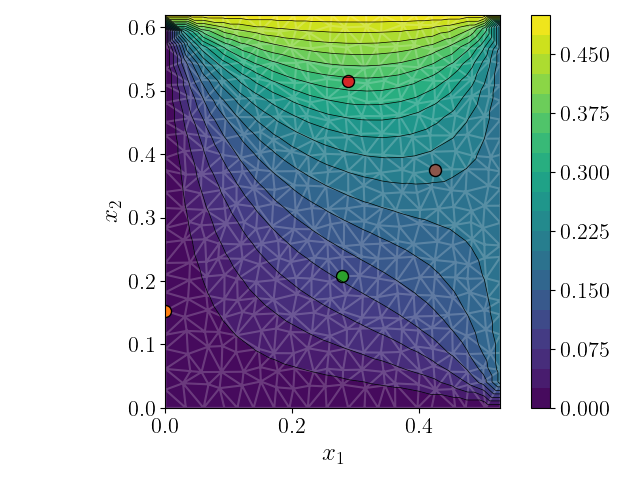
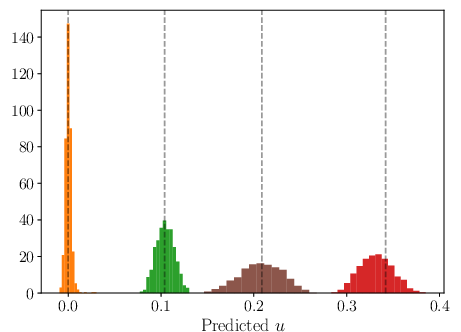
Figure 2: (a) Four selected query locations for the sampled predictive solutions given data, the full field estimations are in Figure 3.

Observational Noise Estimation

GABI extends naturally to joint estimation of observational noise parameters. The latent posterior is augmented to include noise variables, and the pushforward theorem ensures correct posterior sampling in the solution-noise space.

Implementation Details

The framework is agnostic to neural architecture, but requires geometry-aware encoders/decoders, fixed-dimensional latent mappings, and non-locality. Graph Convolutional Networks (GCNs), Generalized Aggregation Networks (GENs), and Transformers are all tested. ABC sampling is preferred for posterior inference due to its parallelizability and efficiency in low-dimensional observation spaces.

Numerical Experiments

Steady-State Heat on Rectangles

GABI is trained on 1k solutions of the heat equation over rectangles with varying dimensions and boundary conditions. At inference, it reconstructs the full field from sparse observations, achieving predictive accuracy comparable to supervised direct map methods and outperforming Gaussian Process (GP) baselines in uncertainty calibration.

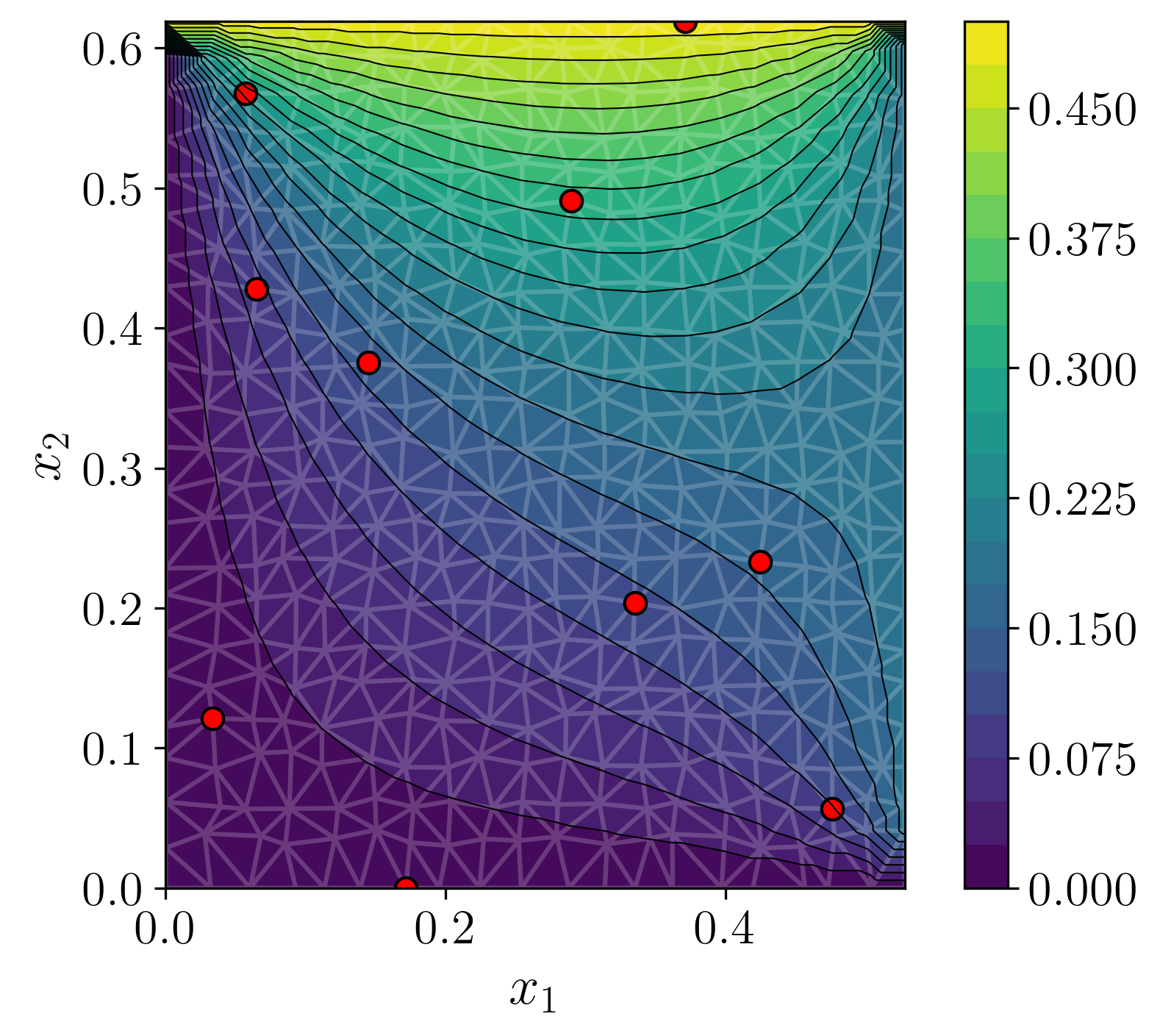
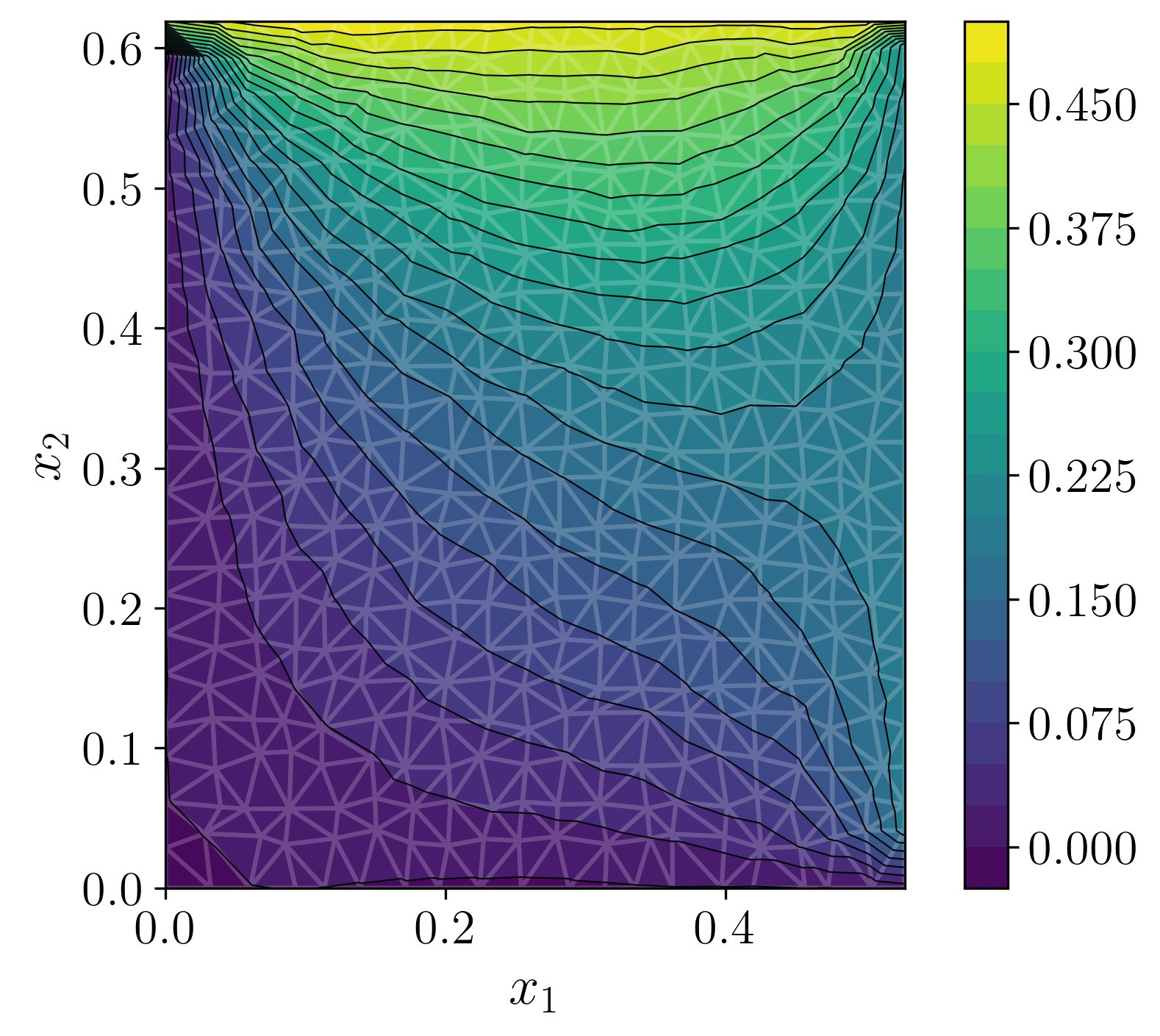
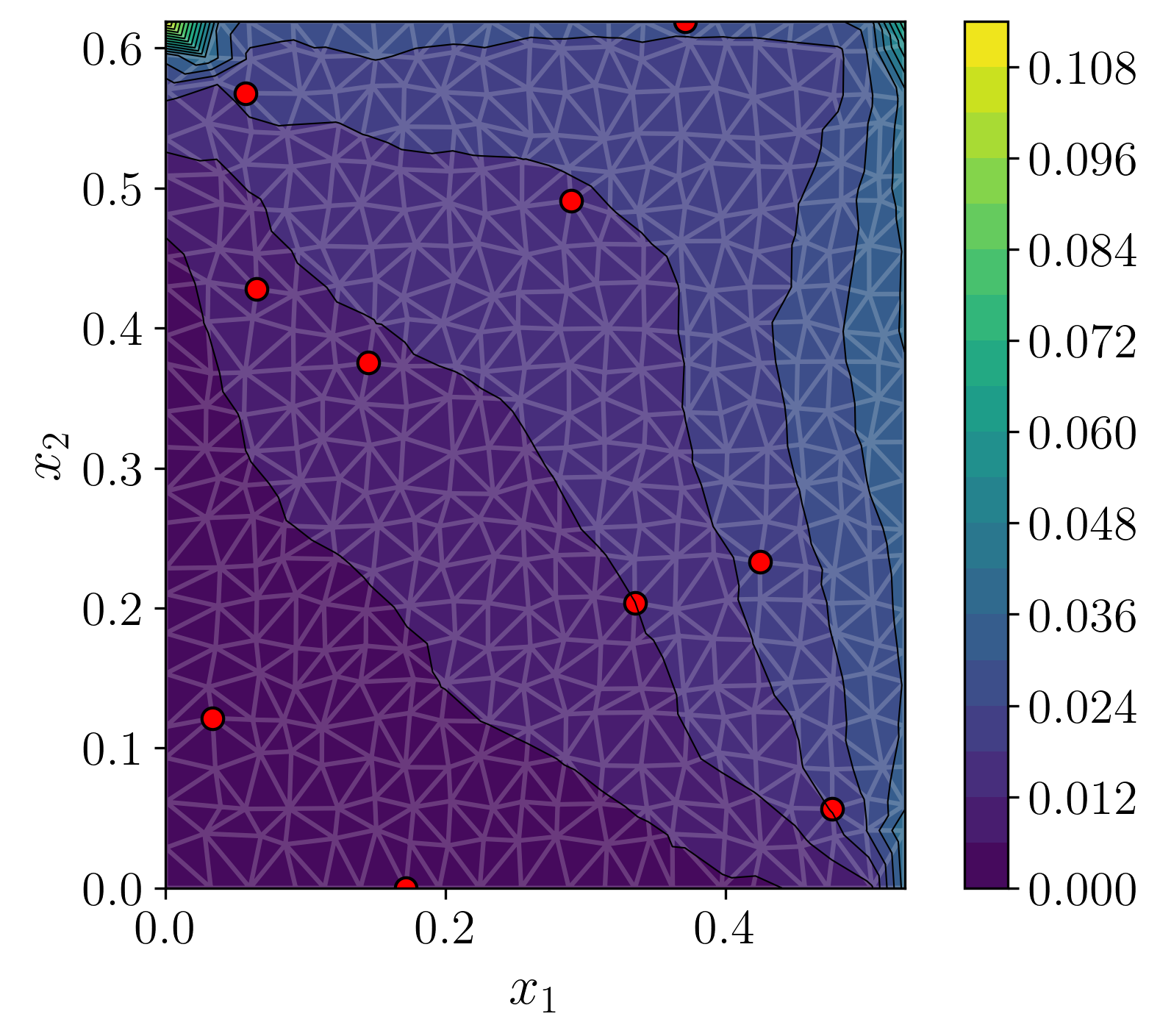
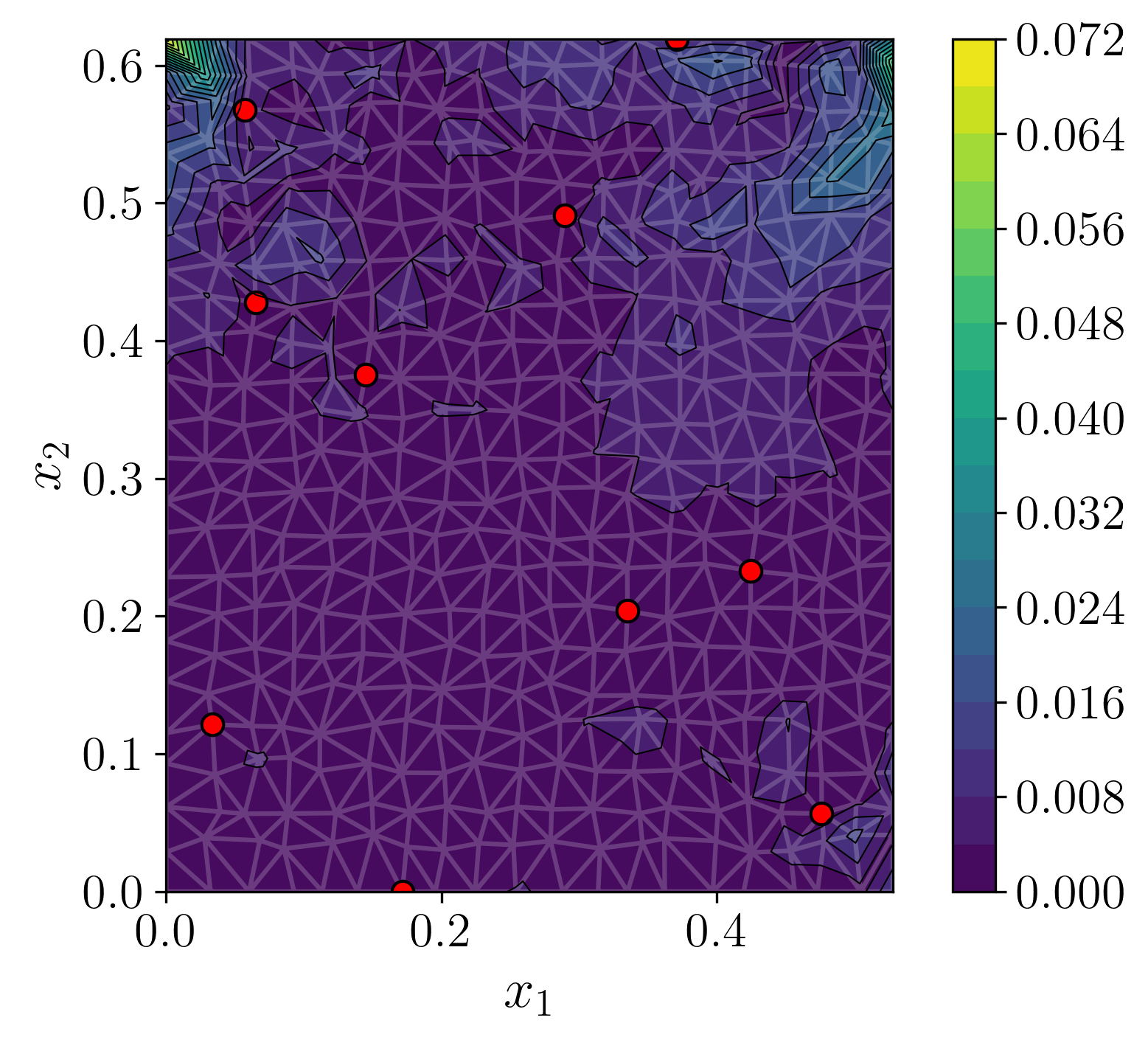
Figure 3: For the heat setup, we overlay in red the observation locations. (a) ground truth (b) decoded mode of predictive posterior. (c) empirical standard deviation of decoded posterior samples. (d) error between decoded mode and ground truth.

Airfoil Flow Field Reconstruction

GABI is trained on RANS simulations of flow around 1k airfoil geometries. From sparse pressure observations on the airfoil surface, it reconstructs pressure and velocity fields. The method achieves similar MAE to direct map methods, with well-calibrated uncertainty quantification.

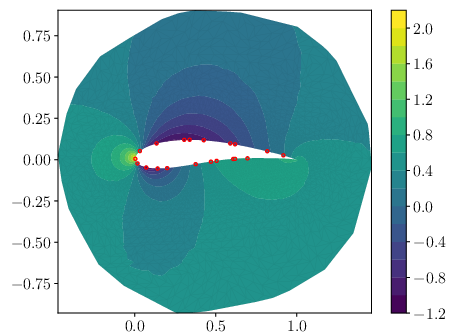
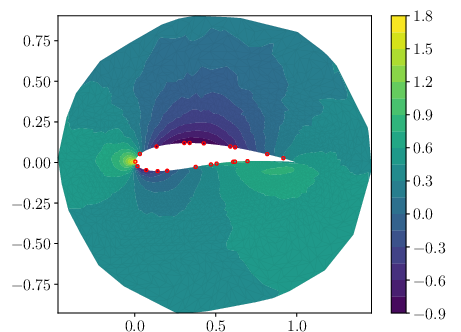
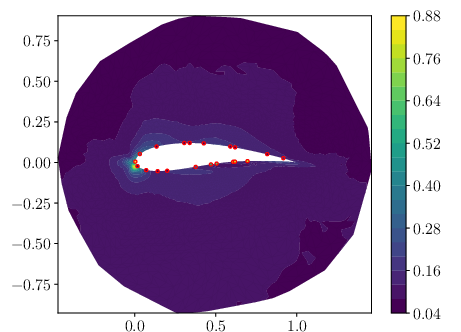
Figure 4: Comparison of ground truth (GT), inferred mean, error, and standard deviation for pressure (p). The red dots correspond to the observation location for the pressure.

Car Body Acoustic Resonance and Source Localization

GABI reconstructs both vibration amplitude and source localization on 3D car bodies from sparse measurements. It significantly outperforms direct map methods in both field and source recovery, demonstrating the advantage of geometry-aware priors.

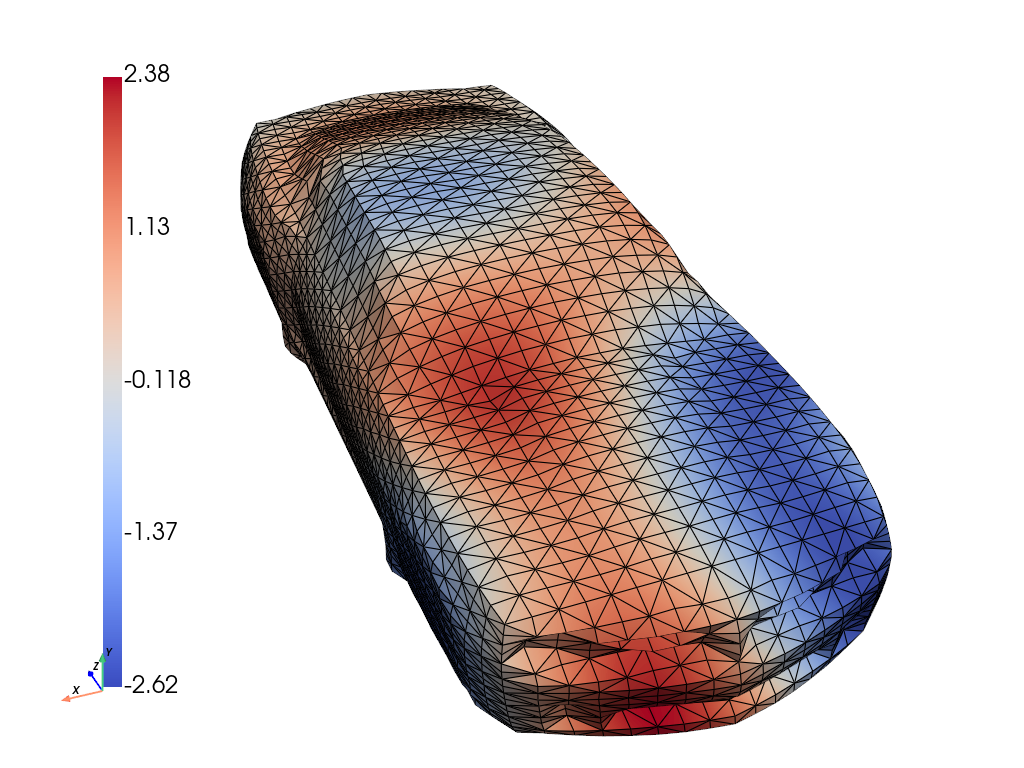
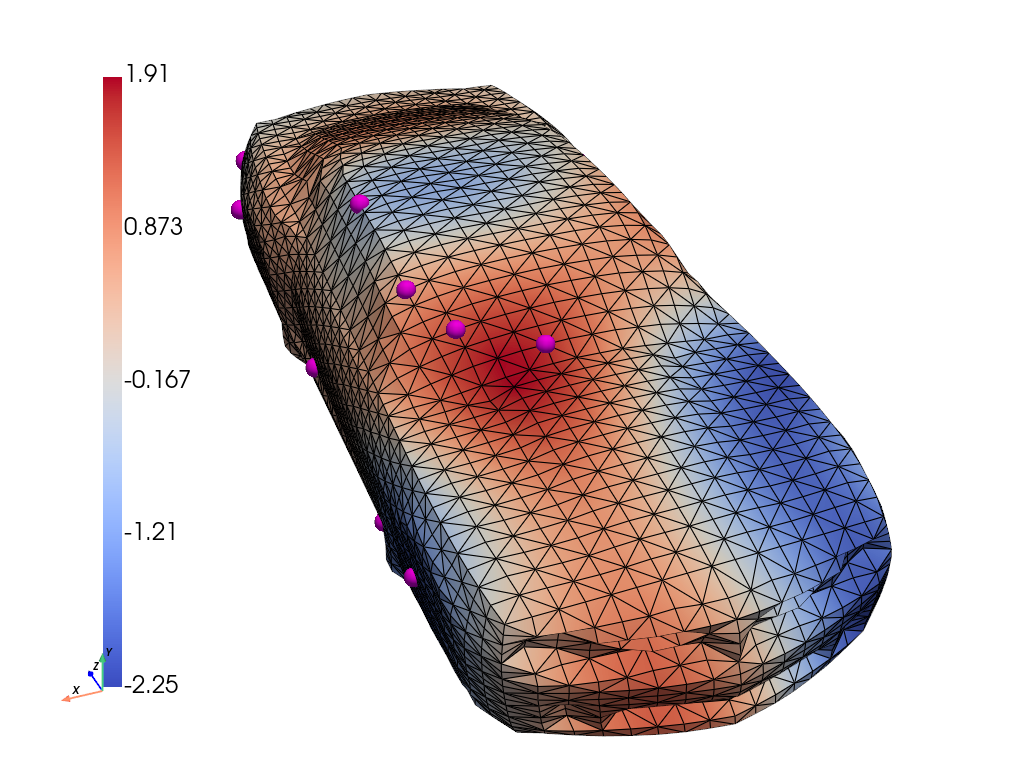
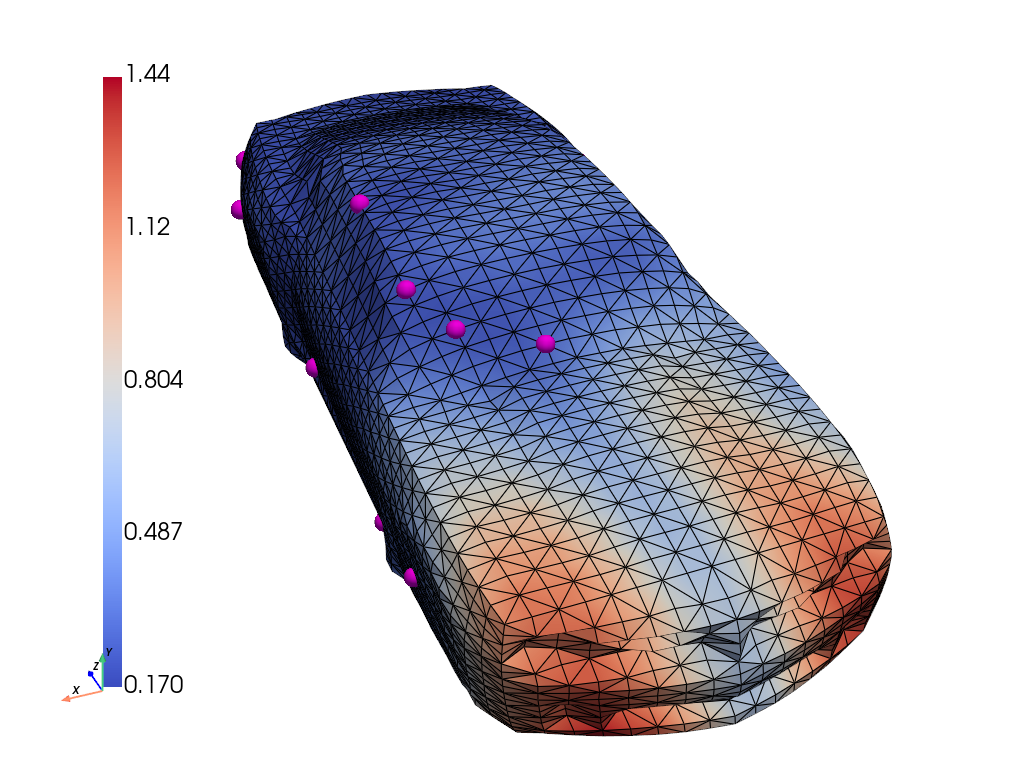
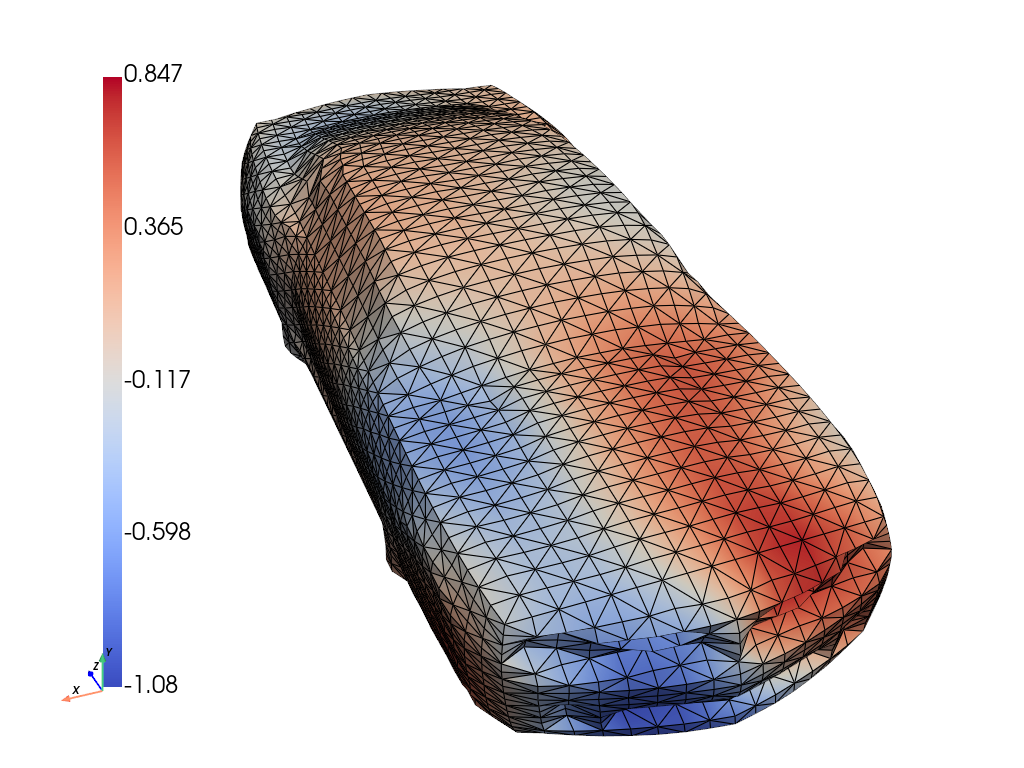
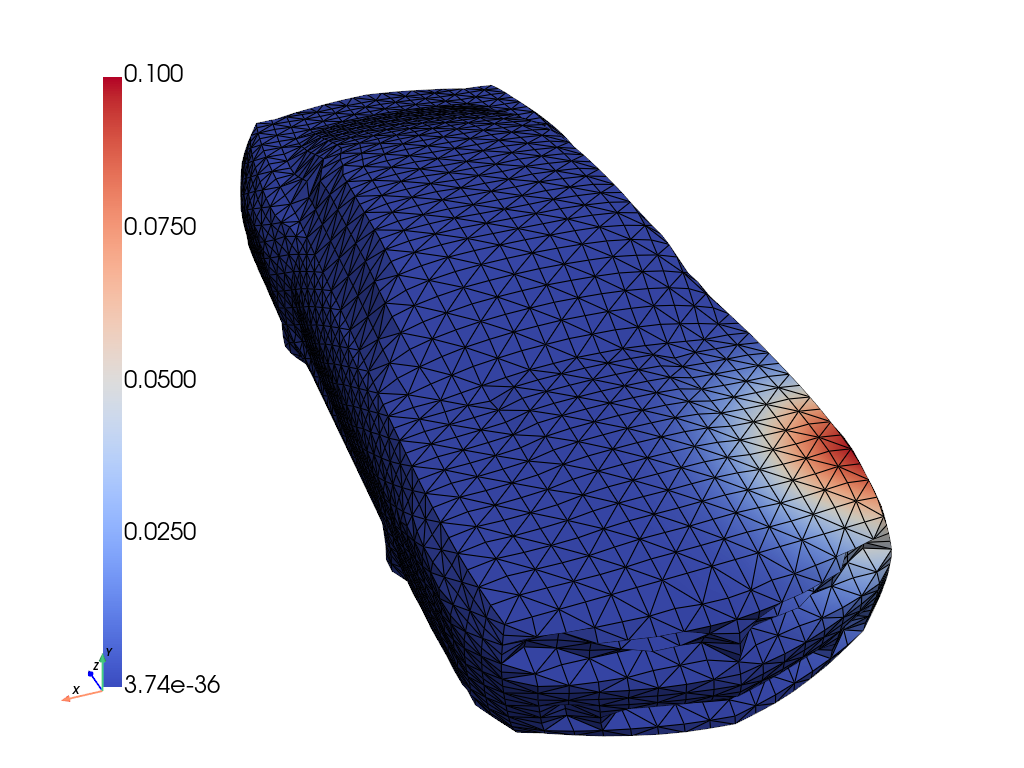
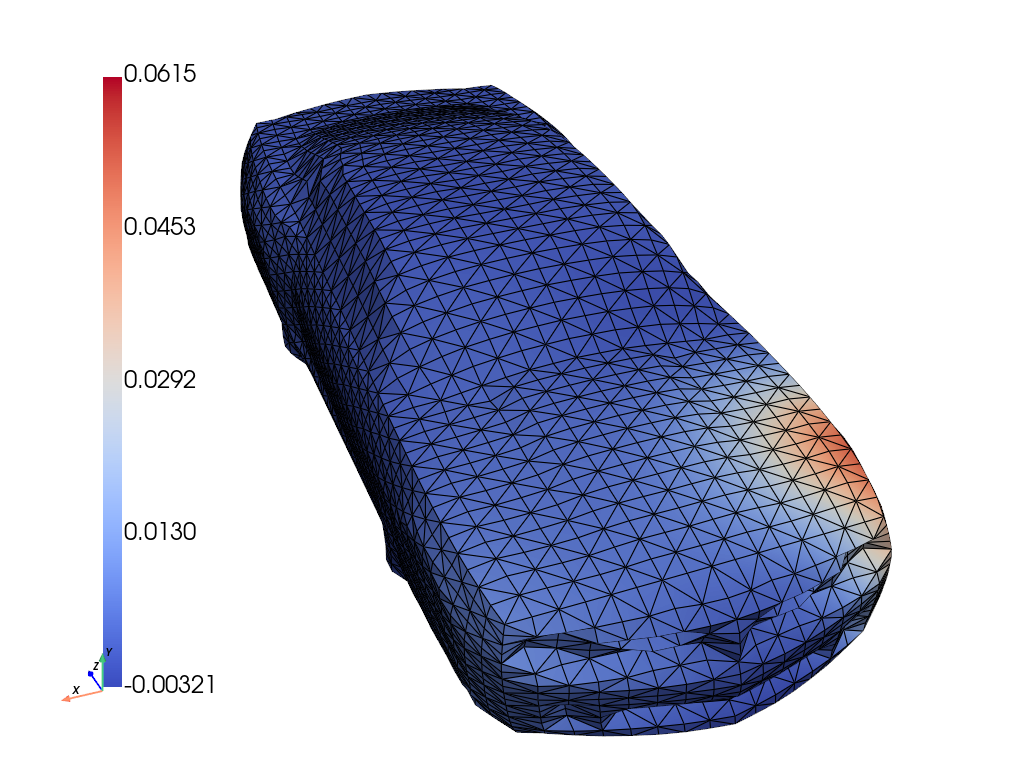
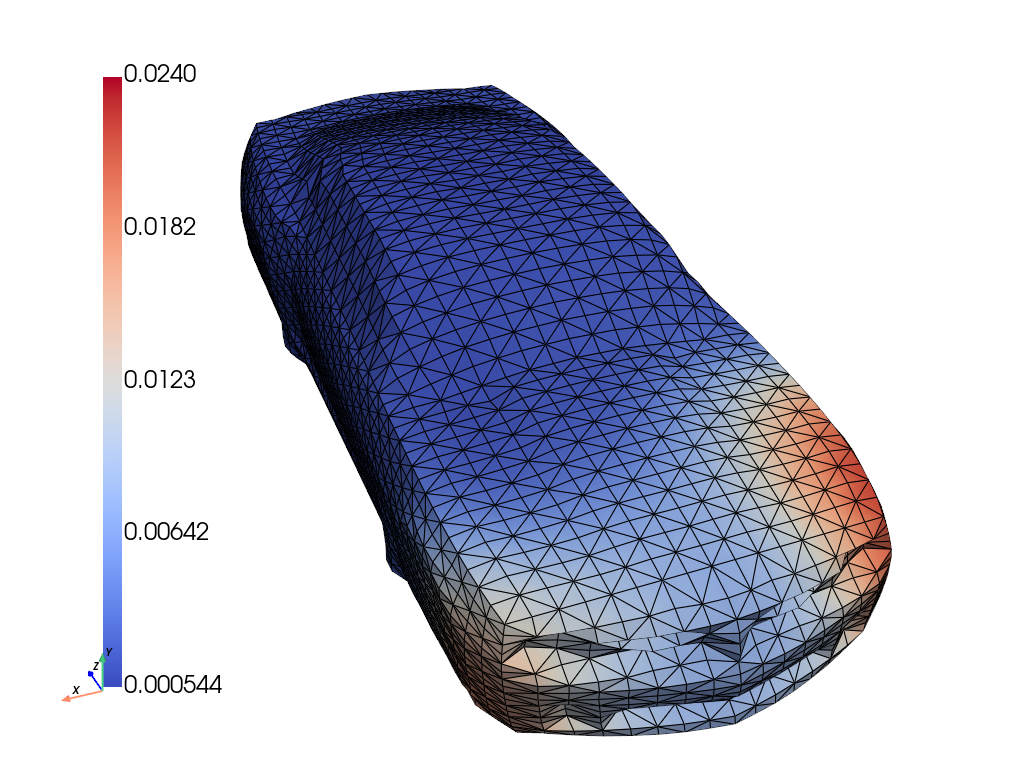
Figure 5: Ground truth, inferred mean, stddev., and error for amplitude u, and forcing f. In magenta are the observation locations.

Large-Scale Terrain Flow

GABI is scaled to 5k+ RANS simulations over complex terrain, using multi-GPU training and inference. It reconstructs pressure and velocity fields from sparse observations, demonstrating scalability and generalization to highly variable geometries.

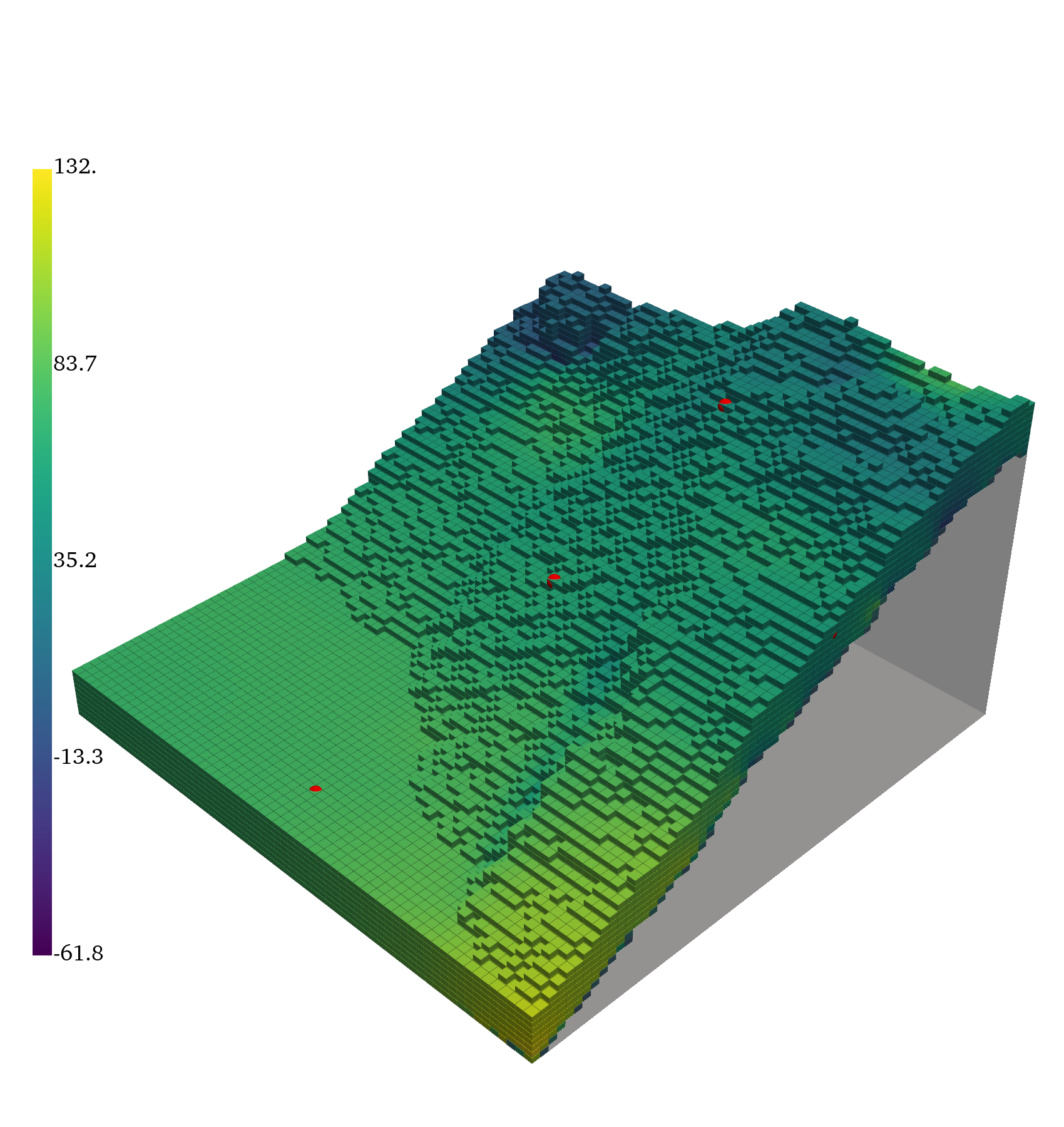
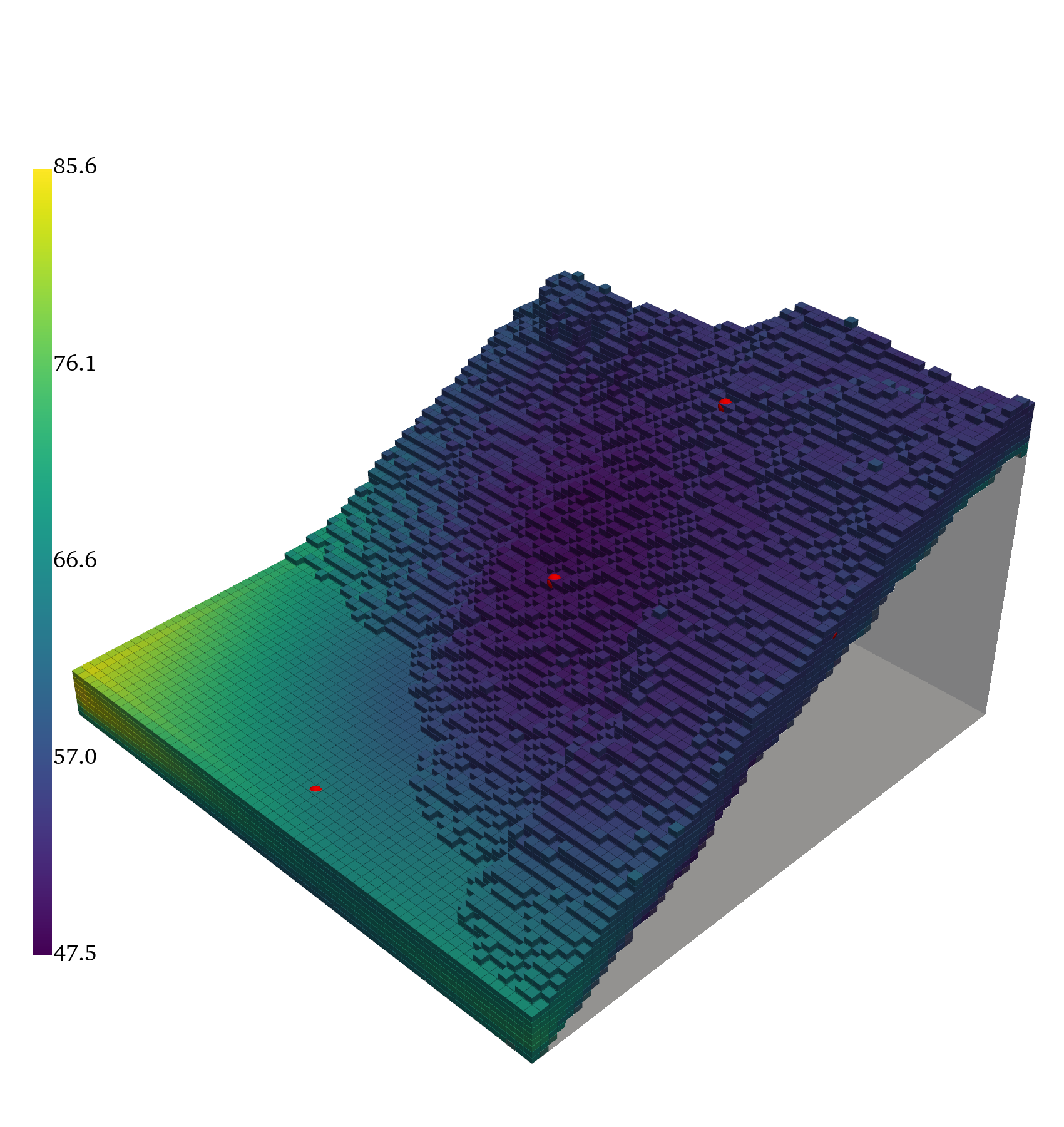
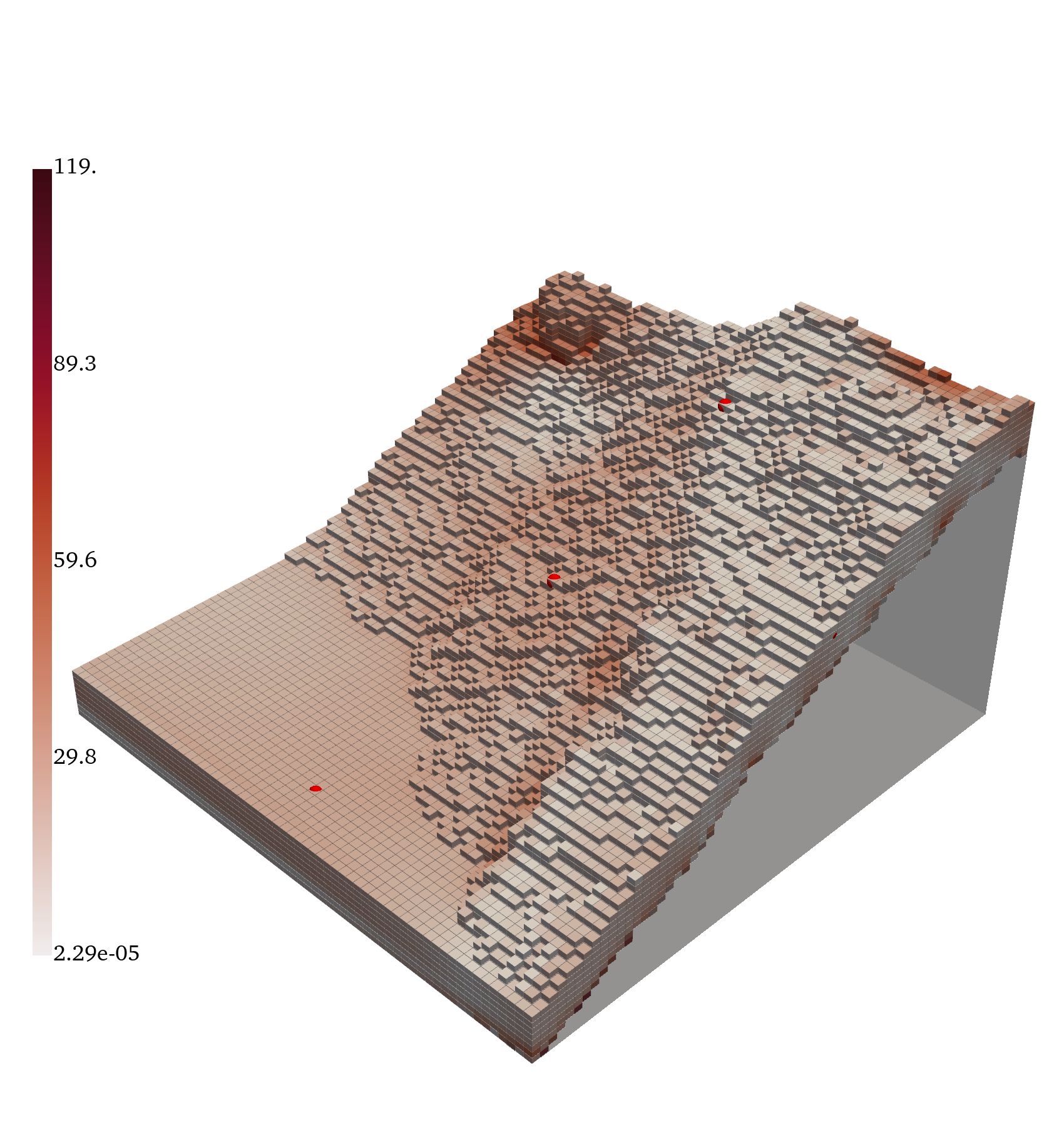
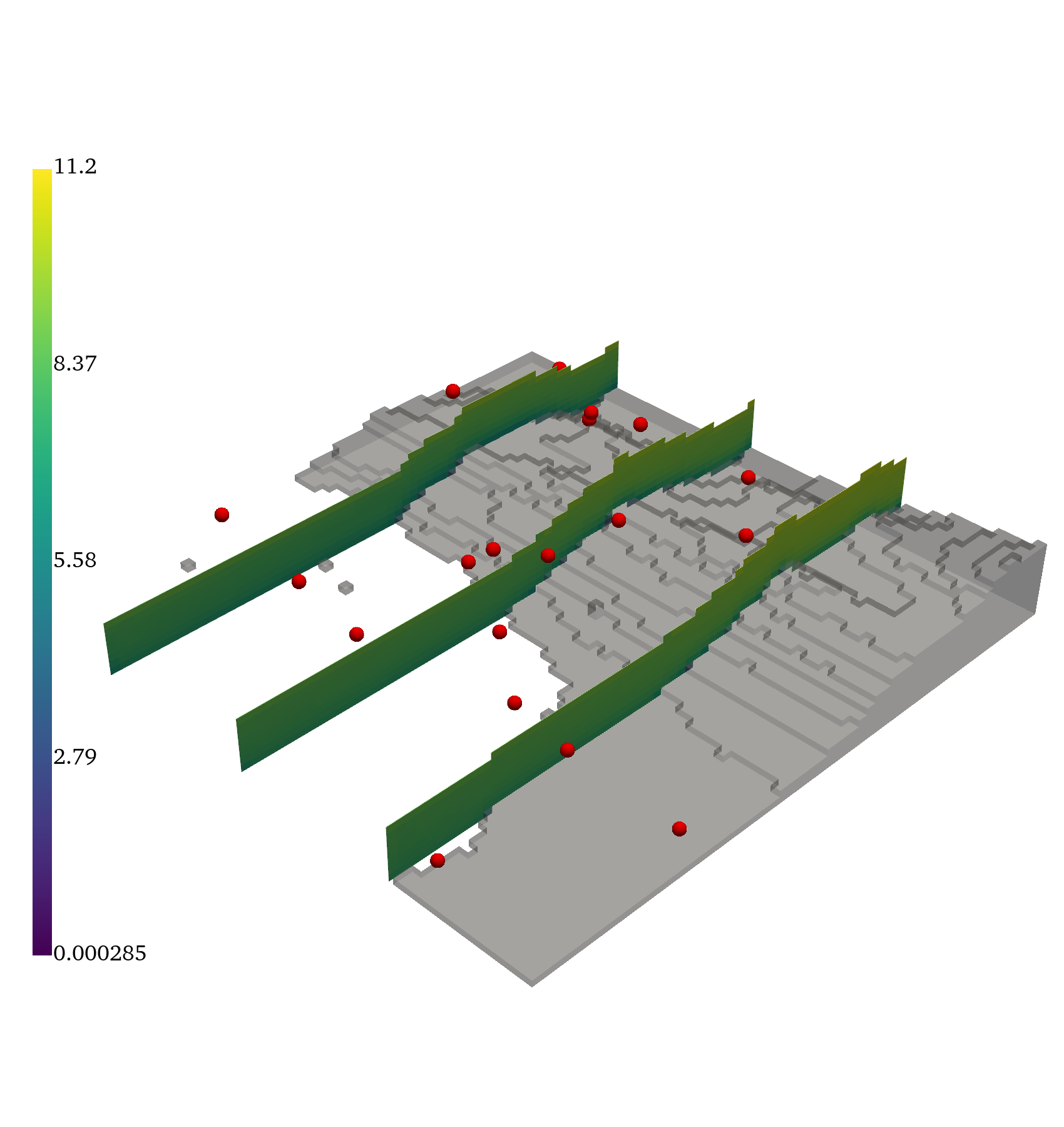
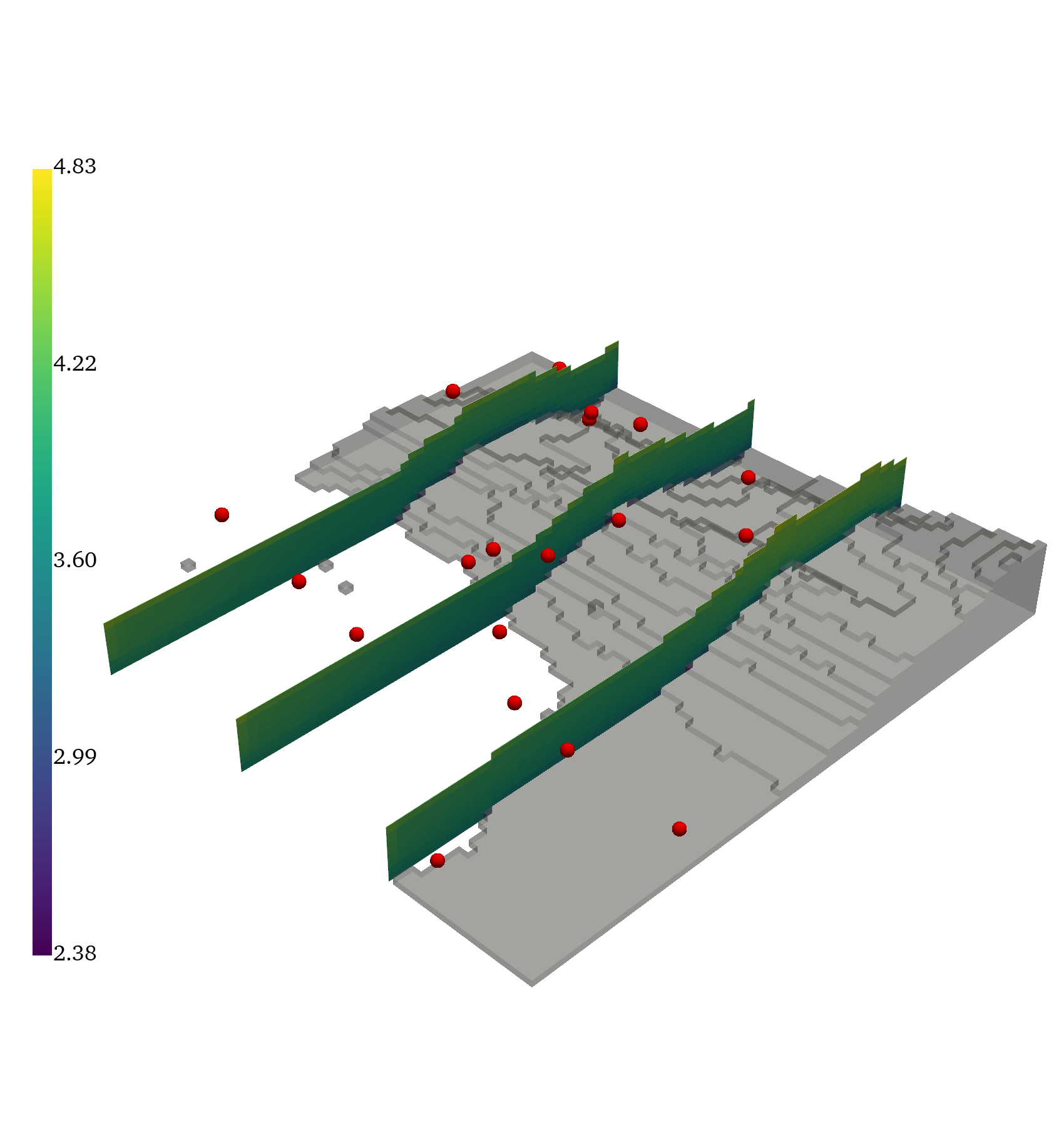
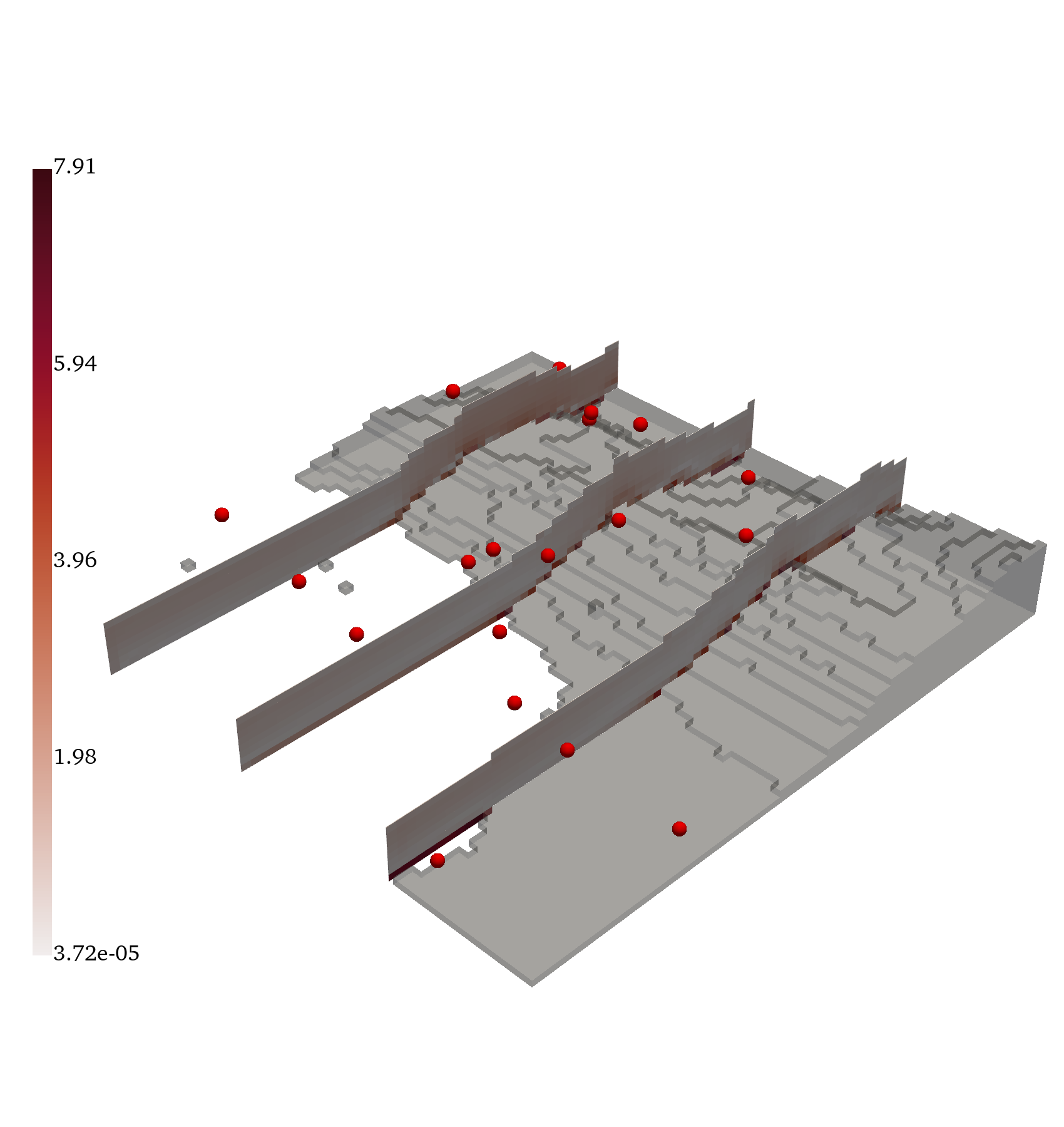
Figure 6: Ground truth, inferred mean, error, and standard deviation for pressure and the magnitude of the velocity vector, ($\|{v}\|$).

Comparative Analysis

Across all tasks, GABI matches or exceeds the predictive accuracy of supervised direct map methods, with the added benefit of robust uncertainty quantification. Unlike direct map or Bayesian neural network approaches, GABI's prior is independent of the observation process, enabling train-once-use-anywhere deployment. GP baselines are consistently outperformed in both accuracy and uncertainty calibration, especially as geometric complexity increases.

Theoretical and Practical Implications

The pushforward prior theorem provides a rigorous foundation for geometry-conditioned Bayesian inversion, enabling the use of learned generative models as priors in arbitrary geometries. The decoupling of prior learning from observation process specification is a major practical advantage, facilitating flexible deployment in engineering and scientific applications where measurement modalities vary.

The architecture-agnostic nature of GABI allows integration with state-of-the-art geometric deep learning models, and the ABC sampling strategy leverages modern GPU hardware for scalable inference. The framework is extensible to joint estimation of nuisance parameters (e.g., noise), and can be adapted to other inverse problems with complex data-generating processes.

Future Directions

Potential future developments include:

• Extension to time-dependent and multi-physics problems.
• Integration with physics-informed neural operators for hybrid data/model-driven priors.
• Exploration of more expressive latent distributions and advanced divergence measures.
• Application to experimental datasets with real measurement noise and missing data.
• Development of foundation models for engineering inversion tasks, leveraging large-scale simulation and experimental data.

Conclusion

GABI provides a principled, flexible, and scalable framework for Bayesian inversion in systems with complex and variable geometries. By learning geometry-aware generative priors and decoupling prior specification from observation process, it enables robust full-field reconstruction and uncertainty quantification from sparse data. The method is validated across diverse physical systems and demonstrates strong performance relative to both supervised and probabilistic baselines. Its theoretical foundation and practical advantages position it as a promising approach for real-world engineering and scientific inference tasks.