GeoSVR: Taming Sparse Voxels for Geometrically Accurate Surface Reconstruction (2509.18090v1)

Abstract: Reconstructing accurate surfaces with radiance fields has achieved remarkable progress in recent years. However, prevailing approaches, primarily based on Gaussian Splatting, are increasingly constrained by representational bottlenecks. In this paper, we introduce GeoSVR, an explicit voxel-based framework that explores and extends the under-investigated potential of sparse voxels for achieving accurate, detailed, and complete surface reconstruction. As strengths, sparse voxels support preserving the coverage completeness and geometric clarity, while corresponding challenges also arise from absent scene constraints and locality in surface refinement. To ensure correct scene convergence, we first propose a Voxel-Uncertainty Depth Constraint that maximizes the effect of monocular depth cues while presenting a voxel-oriented uncertainty to avoid quality degradation, enabling effective and robust scene constraints yet preserving highly accurate geometries. Subsequently, Sparse Voxel Surface Regularization is designed to enhance geometric consistency for tiny voxels and facilitate the voxel-based formation of sharp and accurate surfaces. Extensive experiments demonstrate our superior performance compared to existing methods across diverse challenging scenarios, excelling in geometric accuracy, detail preservation, and reconstruction completeness while maintaining high efficiency. Code is available at https://github.com/Fictionarry/GeoSVR.

• The paper presents an explicit sparse voxel framework that overcomes Gaussian Splatting limitations by leveraging adaptive uncertainty constraints for precise geometry.
• The method integrates voxel dropout and surface rectification techniques to enhance detail preservation and ensure global consistency in reconstruction.
• Experiments on DTU, Tanks and Temples, and Mip-NeRF 360 datasets show state-of-the-art performance with improvements in Chamfer distance, F1-score, and other key metrics.

GeoSVR: Explicit Sparse Voxel Framework for Geometrically Accurate Surface Reconstruction

Introduction and Motivation

GeoSVR introduces an explicit sparse voxel-based framework for surface reconstruction, addressing representational bottlenecks inherent in Gaussian Splatting (3DGS) approaches. While 3DGS methods have achieved efficiency and quality in radiance field-based reconstruction, they suffer from initialization dependencies and ambiguous geometry representation, particularly in regions with poor point cloud coverage or weak texture. GeoSVR leverages the SVRaster paradigm, initializing scenes with fully covered sparse voxels, thus ensuring geometric completeness and clarity. The method is designed to overcome two principal challenges: lack of native scene constraints and the locality of voxel-based surface refinement.

Figure 1: GeoSVR achieves high-quality surface reconstruction for complex real-world scenes, outperforming Gaussian Splatting-based methods in detail, completeness, and efficiency.

Methodology

Sparse Voxel Representation and Rendering

GeoSVR builds upon SVRaster, representing scenes as an octree of sparse voxels, each parameterized by SH coefficients for color and trilinear densities at voxel corners for geometry. Rendering is performed via $\alpha$-blending, with trilinear interpolation of densities and colors along sampled ray segments. Adaptive octree control is employed, pruning voxels with low blending weights and subdividing those with high gradient priorities to capture finer details.

Voxel-Uncertainty Depth Constraint

To enforce robust scene constraints, GeoSVR introduces a Voxel-Uncertainty Depth Constraint. Unlike prior works relying on SDF or point cloud priors, GeoSVR utilizes monocular depth cues from foundation models (e.g., DepthAnythingV2), modulated by a level-aware geometric uncertainty metric. This uncertainty is computed as a function of voxel octree level and local density, adaptively weighting the influence of external depth supervision. The constraint is applied via a patch-wise depth loss, ensuring that high-uncertainty regions rely more on external cues, while confident regions are governed by photometric consistency.

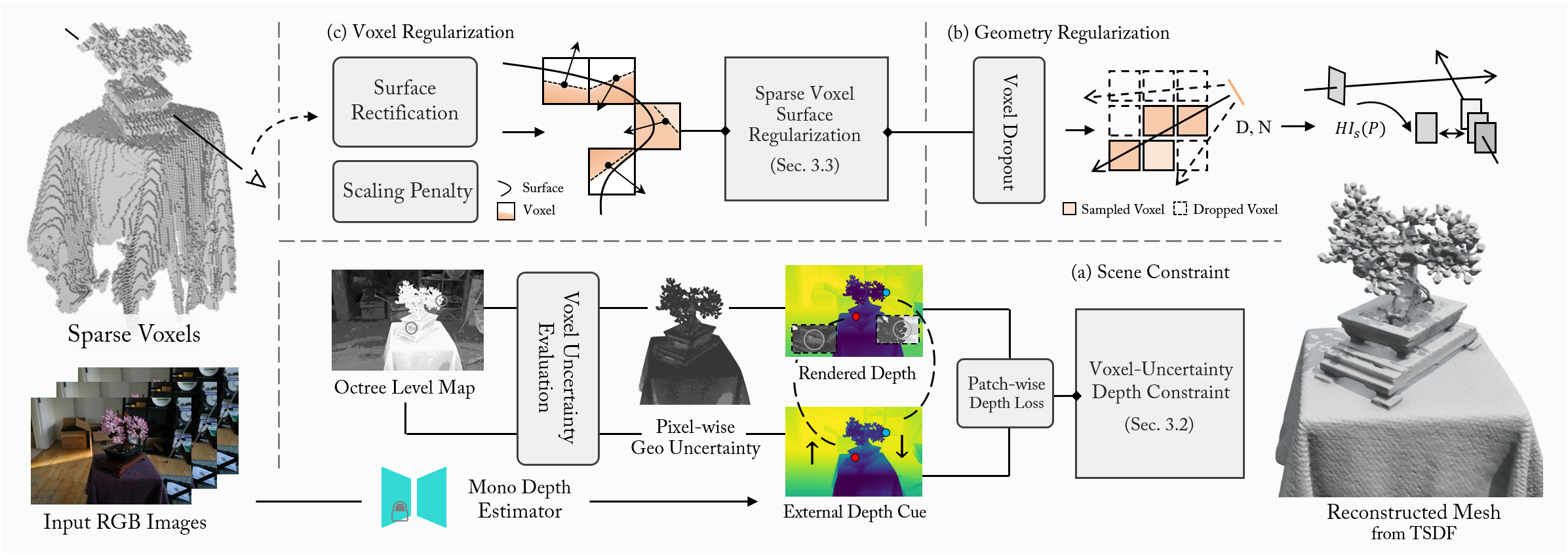
Figure 2: GeoSVR pipeline: (a) Voxel-Uncertainty Depth Constraint for adaptive scene convergence, (b) Voxel Dropout for global geometry consistency, (c) Voxel Regularization for sharp surface formation.

Sparse Voxel Surface Regularization

GeoSVR introduces several regularization strategies to refine geometric accuracy:

• Multi-view Regularization with Voxel Dropout: Homography-based patch warping is applied for explicit geometric consistency, but its effectiveness is limited by voxel locality. GeoSVR randomly drops out voxels during regularization, forcing each voxel to maintain global consistency and mitigating local minima.
• Surface Rectification: To align rendered surfaces with voxel densities, GeoSVR penalizes density discrepancies at voxel entry/exit points along rays, ensuring sharp segmentation between surfaces and empty space.
• Scaling Penalty: Large voxels, which are less accurate in geometry modeling, are penalized based on their size relative to the minimal voxel size, further promoting surface sharpness.

Experimental Results

Quantitative and Qualitative Evaluation

GeoSVR is evaluated on DTU, Tanks and Temples (TnT), and Mip-NeRF 360 datasets. It consistently outperforms state-of-the-art implicit (NeuS, Neuralangelo, Geo-NeuS) and explicit (2DGS, GOF, PGSR) methods in geometric accuracy, detail preservation, and completeness, while maintaining competitive training and inference efficiency.

• DTU: GeoSVR achieves the lowest Chamfer distance (0.47), surpassing all baselines, including those leveraging external geometry cues.
• TnT: GeoSVR attains the highest F1-score (0.56), demonstrating robustness across diverse real-world scenarios.
• Mip-NeRF 360: GeoSVR matches or exceeds the best surface reconstruction methods in PSNR, SSIM, and LPIPS metrics for novel view synthesis.

  Figure 3: Mesh reconstructions on DTU show GeoSVR's superior accuracy and completeness, especially in challenging regions.

  

  Figure 4: Mesh reconstructions on Tanks and Temples highlight GeoSVR's ability to recover intricate details and precise flats.

Ablation Studies

Ablation experiments confirm the effectiveness of each component:

• Patch-wise depth loss significantly improves geometry over sparse depth or inverse depth constraints.
• Voxel-Uncertainty Depth Constraint further refines uncertain regions without degrading well-reconstructed areas.
• Voxel Dropout enhances multi-view regularization, breaking local traps and improving global consistency.
• Surface Rectification and Scaling Penalty facilitate sharp, accurate surface formation.

  Figure 5: Reconstruction comparison in challenging regions, demonstrating the impact of scene constraint.

  

  Figure 6: Qualitative comparison on Mip-NeRF 360, showing GeoSVR's detailed and complete surface recovery.

Implementation Considerations

GeoSVR is implemented in PyTorch with CUDA kernels, leveraging efficient octree management and rasterization. Training is performed with Adam optimizer, using 20,000 iterations and learning rates tailored for density and SH coefficients. Depth cues are provided by DepthAnythingV2, and mesh extraction utilizes TSDF. The method achieves high inference speed (up to 143.8 FPS on DTU) and moderate GPU memory consumption (11.2 GB peak), with mesh extraction times within minutes.

Trade-offs and Limitations

• Globality vs. Locality: While voxel dropout and regularization mitigate local minima, further enhancement of voxel globality is needed for textureless or reflective regions.
• Photometric Consistency: Accurate geometry may conflict with appearance rendering in regions with photometric inconsistency (e.g., reflections, transparency).
• Initialization Independence: GeoSVR's prior-free initialization enables recovery in regions where 3DGS fails due to poor point cloud coverage, but may require more sophisticated constraints for highly ambiguous scenes.

Implications and Future Directions

GeoSVR demonstrates that explicit sparse voxel representations, when combined with adaptive uncertainty-driven constraints and targeted regularization, can surpass Gaussian Splatting-based methods in surface reconstruction. The approach is well-suited for integration with geometric foundation models, enabling robust reconstruction in previously challenging scenarios. Future work should focus on enhancing voxel globality, incorporating efficient ray tracing for complex materials, and addressing transparency and photometric inconsistency.

Figure 7: Visualization of reconstructed meshes on TnT, illustrating GeoSVR's performance in complex scenes.

Figure 8: Visualization of reconstructed meshes on Mip-NeRF 360, showing completeness and detail.

Figure 9: Visualization of reconstructed meshes on DTU, highlighting fine-grained surface recovery.

Figure 10: Vertex-colored mesh visualization on DTU, demonstrating vivid and accurate object reconstruction.

Conclusion

GeoSVR establishes a new paradigm for explicit sparse voxel-based surface reconstruction, achieving state-of-the-art accuracy, completeness, and detail preservation. Its uncertainty-driven constraints and regularization strategies enable robust geometry recovery, even in regions where prior methods fail. The framework is efficient and scalable, with practical implications for real-world 3D reconstruction tasks. Future research should address remaining challenges in global consistency, photometric ambiguity, and material complexity to further advance the field.