Variation in Verification: Understanding Verification Dynamics in Large Language Models (2509.17995v1)

Abstract: Recent advances have shown that scaling test-time computation enables LLMs to solve increasingly complex problems across diverse domains. One effective paradigm for test-time scaling (TTS) involves LLM generators producing multiple solution candidates, with LLM verifiers assessing the correctness of these candidates without reference answers. In this paper, we study generative verifiers, which perform verification by generating chain-of-thought (CoT) reasoning followed by a binary verdict. We systematically analyze verification dynamics across three dimensions - problem difficulty, generator capability, and verifier generation capability - with empirical studies on 12 benchmarks across mathematical reasoning, knowledge, and natural language reasoning tasks using 14 open-source models (2B to 72B parameter range) and GPT-4o. Our experiments reveal three key findings about verification effectiveness: (1) Easy problems allow verifiers to more reliably certify correct responses; (2) Weak generators produce errors that are easier to detect than strong generators; (3) Verification ability is generally correlated with the verifier's own problem-solving capability, but this relationship varies with problem difficulty. These findings reveal opportunities to optimize basic verification strategies in TTS applications. First, given the same verifier, some weak generators can nearly match stronger ones in post-verification TTS performance (e.g., the Gemma2-9B to Gemma2-27B performance gap shrinks by 75.5%). Second, we identify cases where strong verifiers offer limited advantage over weak ones, as both fail to provide meaningful verification gains, suggesting that verifier scaling alone cannot overcome fundamental verification challenges.

• The paper demonstrates that easier problems boost true positive rates, highlighting problem difficulty as a key factor in verification performance.
• The paper shows that generator capability modulates error detection, with stronger generators producing subtler errors that lower true negative rates.
• The paper finds that verifier performance is regime-dependent, revealing diminishing returns when scaling verifier capacity for very easy or hard problems.

Variation in Verification: Systematic Analysis of Verification Dynamics in LLMs

Introduction and Motivation

The paper "Variation in Verification: Understanding Verification Dynamics in LLMs" (2509.17995) presents a comprehensive empirical paper of generative verification in LLMs, focusing on the interplay between problem difficulty, generator capability, and verifier generation capability. The motivation stems from the increasing reliance on LLM-based verifiers for scalable, reference-free evaluation in test-time scaling (TTS) scenarios, where candidate solutions are filtered by LLM verifiers without access to ground-truth answers. The work addresses a critical gap: while prior research has established that verifier capability correlates with verification performance, the nuanced effects of problem difficulty and generator capability have not been systematically characterized.

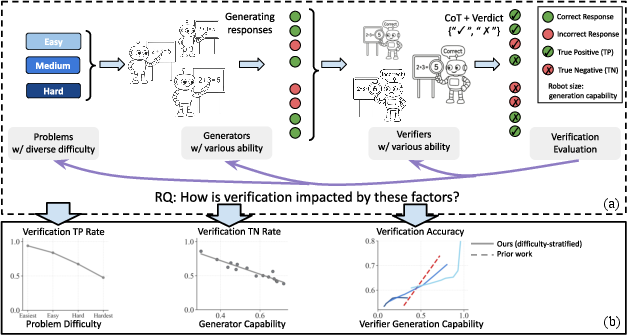
Figure 1: Overview of the paper design, illustrating the generative verification pipeline and the three key factors analyzed: problem difficulty, generator capability, and verifier capability.

Experimental Setup and Methodology

The paper evaluates 14 open-source models (2B–72B parameters) and GPT-4o across 12 benchmarks spanning mathematical reasoning, knowledge QA, and natural language reasoning. Verification is operationalized as a generative process: the verifier produces a chain-of-thought (CoT) trace followed by a binary verdict ("Correct"/"Incorrect"). Metrics include true positive rate (TPR), true negative rate (TNR), and balanced accuracy. Problem difficulty is defined as the average pass rate across diverse generators, providing a model-agnostic measure. Each generator produces 64 responses per problem, and verifiers evaluate balanced subsets of correct and incorrect responses.

Key Findings: Verification Dynamics

1. Problem Difficulty Governs Correctness Recognition

Empirical results demonstrate that TPR increases monotonically with problem easiness, indicating that verifiers are more reliable at certifying correct responses on easy problems. In contrast, TNR exhibits no systematic dependence on problem difficulty, suggesting that error detection is not directly modulated by problem complexity.

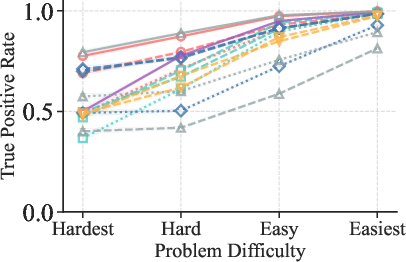
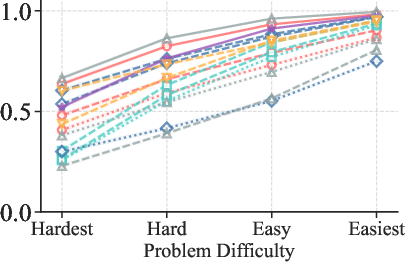
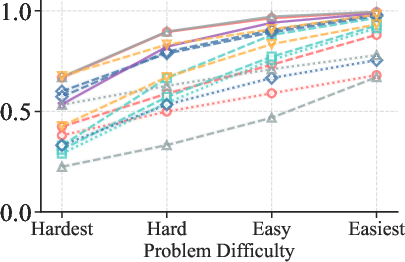
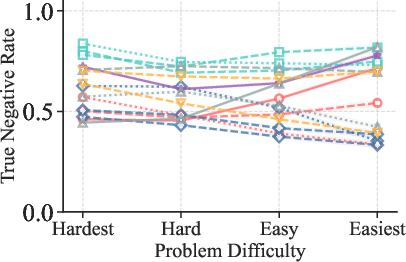
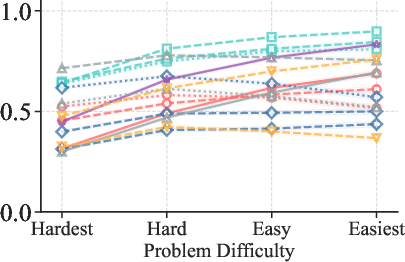
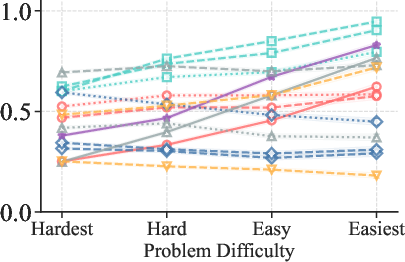
Figure 2: TPR (Mathematics) increases with problem easiness, confirming the strong dependence of correctness recognition on problem difficulty.

2. Generator Capability Modulates Error Detectability

Verification performance is strongly influenced by the generator's capability. Weak generators produce errors that are more easily detected (high TNR), while strong generators generate errors that are more subtle and harder for verifiers to identify (low TNR). TPR remains high across generator strengths, but TNR drops sharply as generator capability increases.

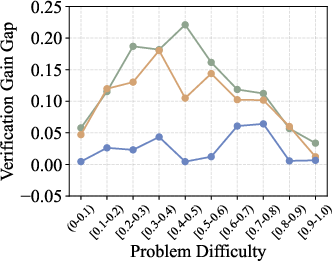
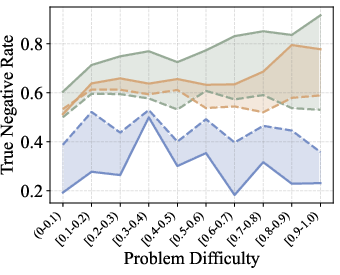
Figure 3: Verif. Gain Gap (Mathematics) illustrates the narrowing gap in verification gain between strong and weak verifiers as generator capability increases.

3. Verifier Capability: Regime-Dependent Correlation

While verifier generation capability is generally correlated with verification performance, the relationship is highly regime-dependent. For medium-difficulty problems, the correlation is linear and strong. For easy problems, a threshold effect emerges: above a certain capability, verification performance saturates. For hard problems, verification accuracy plateaus, and further scaling of verifier capability yields diminishing returns.

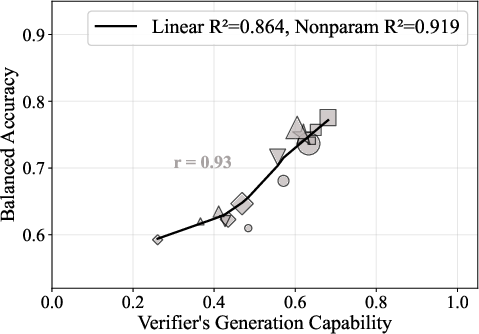
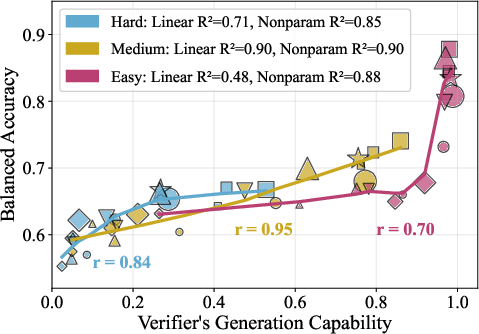
Figure 4: All data (Mathematics) shows the overall correlation between verifier capability and balanced accuracy, with regime-dependent nonlinearity.

Implications for Test-Time Scaling (TTS)

Weak Generators Can Match Strong Generators Post-Verification

In TTS settings, verification enables weak generators to approach the post-verification performance of strong generators. For example, Gemma2-9B narrows its performance gap with Gemma2-27B by 75.5% after verification with a fixed verifier. The largest verification gains are observed for weak-to-medium generators, where high TNR enables effective error filtering.

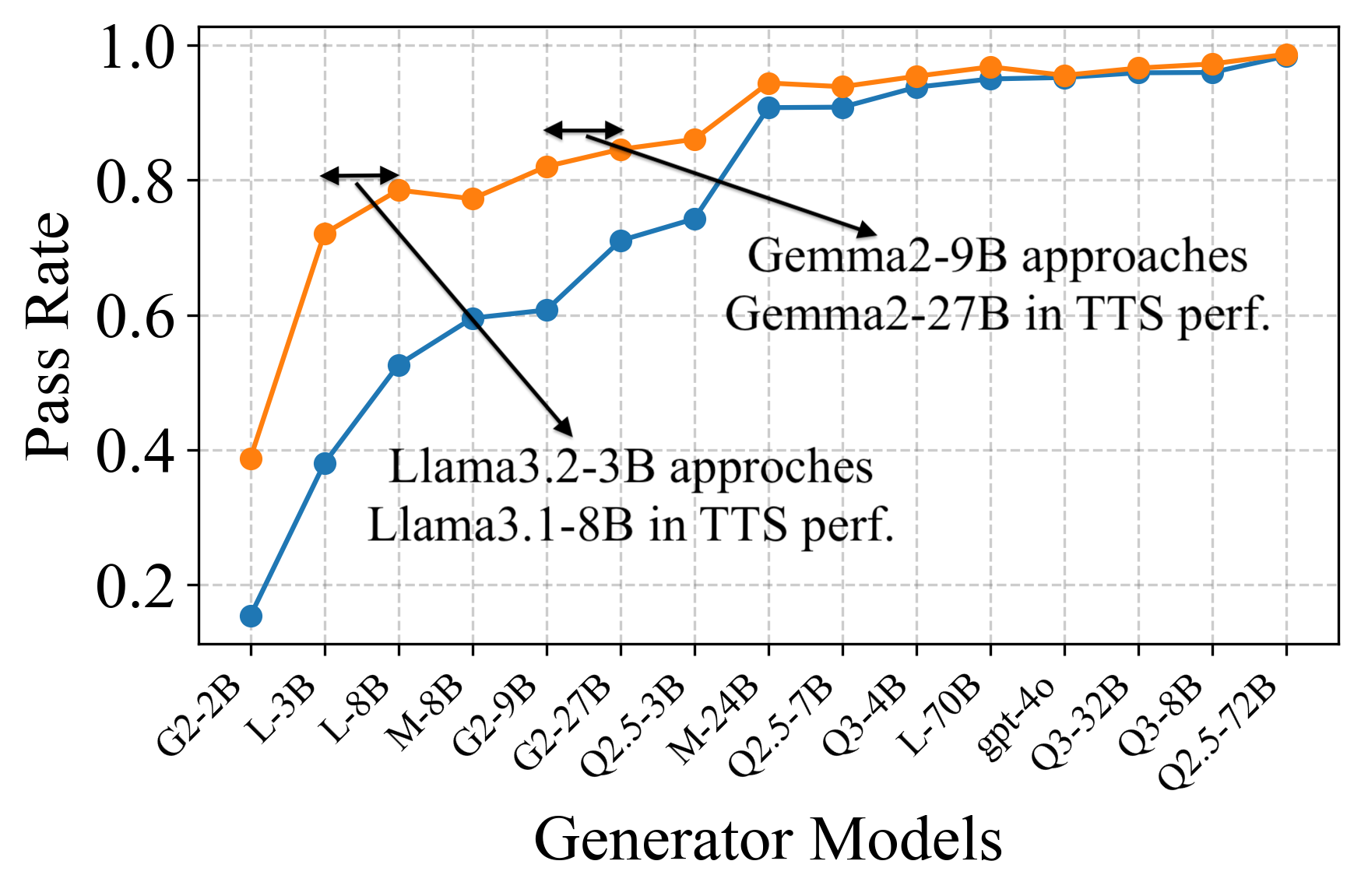
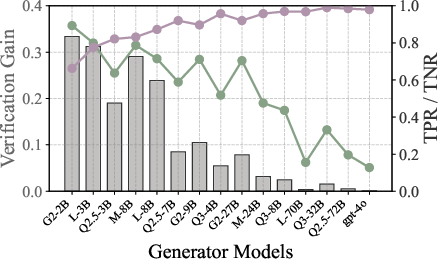
Figure 5: Pass rate (Mathematics) before and after verification, demonstrating substantial gap closure for weak generators.

Weak Verifiers Can Substitute for Strong Verifiers in Specific Regimes

The verification gain gap between strong and weak verifiers narrows in three regimes: easy problems (high TPR for both), strong generators (low TNR for both), and very hard problems (verification accuracy plateaus). In these regimes, scaling verifier capacity does not yield meaningful improvements, indicating that computational resources can be conserved without sacrificing verification quality.

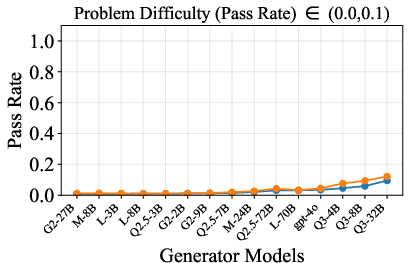
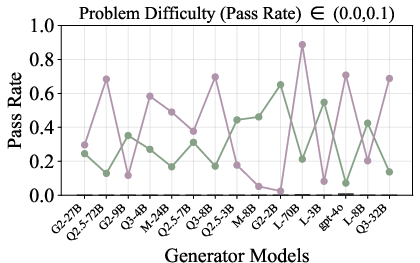
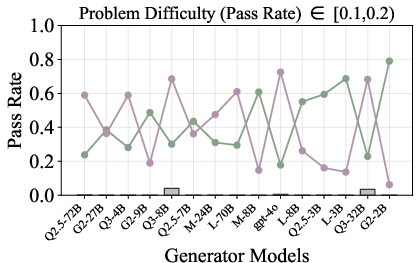
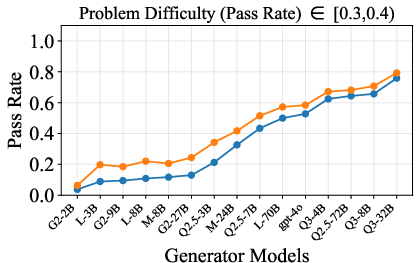
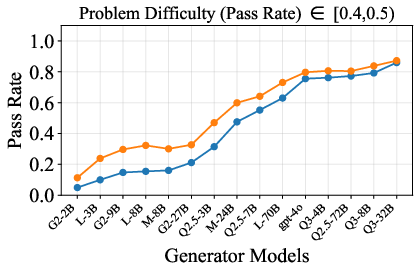
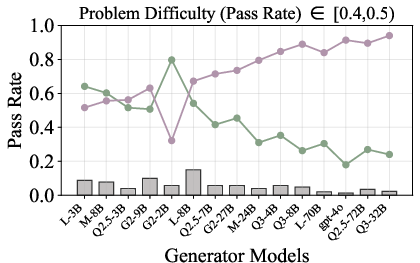
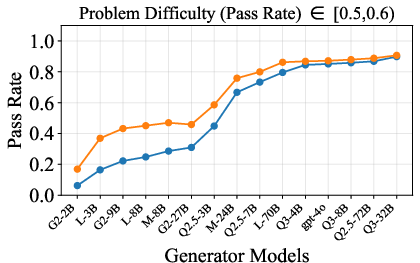
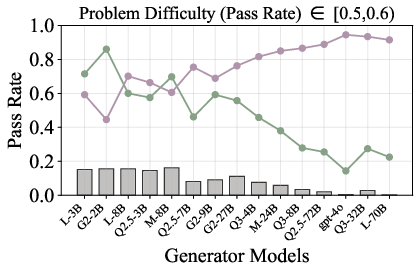
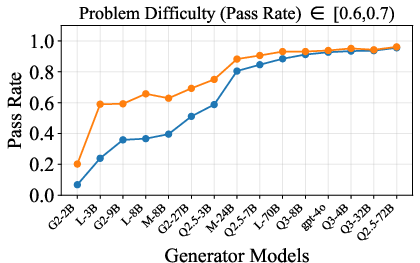
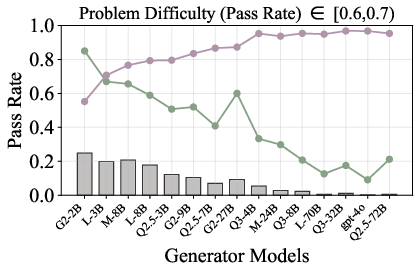
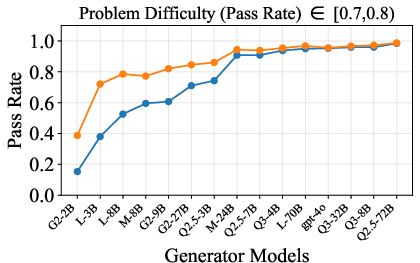
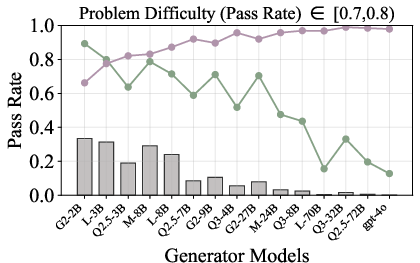
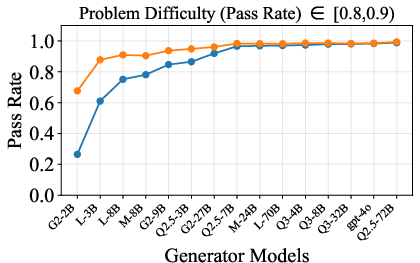
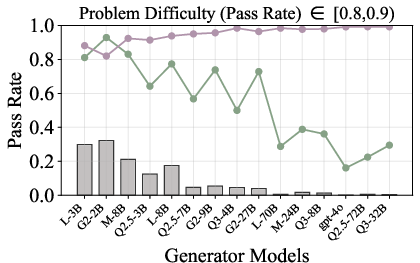
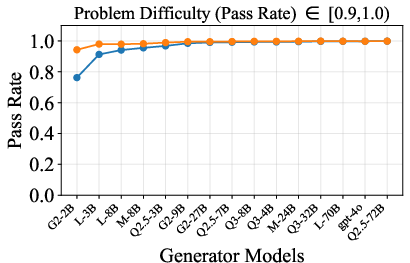
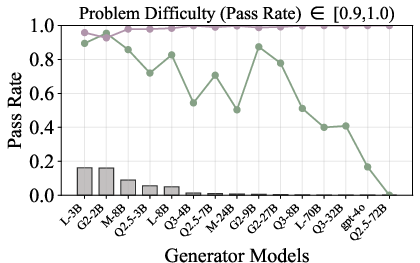
Figure 6: Verification-augmented TTS performance across problem difficulty intervals, showing pass rates and verification gains for Mathematics.

Mechanistic Insights and Case Studies

Case studies reveal that verifiers often employ a "solve-and-match" strategy, generating their own reference solutions for comparison. On hard problems, verifiers frequently fail to solve the problem correctly, leading to false negatives (rejecting correct generator responses). For strong generators, errors are internally consistent and propagate through the reasoning chain, making them difficult for verifiers to detect. Weak generators, in contrast, produce self-contradictory solutions that are more readily rejected.

Theoretical and Practical Implications

The findings challenge the prevailing assumption that scaling verifier capability is universally beneficial. Verification asymmetry—where verifying is easier than generating—does not hold uniformly across all regimes. The results suggest that strategic pairing of generators and verifiers, informed by problem difficulty and generator capability, can optimize computational efficiency in TTS applications. Furthermore, the observed limitations in error detection for strong generators and hard problems highlight fundamental bottlenecks in current generative verification paradigms.

Future Directions

The paper opens several avenues for future research:

• Verifier Architecture: Development of specialized verifier architectures or training objectives that enhance error detection for strong generators.
• Adaptive TTS Strategies: Dynamic allocation of verifier resources based on real-time estimates of problem difficulty and generator capability.
• Benchmarking and Evaluation: Design of new benchmarks that stress-test verification in adversarial and high-difficulty regimes.
• Multi-Agent Verification: Exploration of collaborative or debate-style verification systems to overcome individual verifier limitations.

Conclusion

This work provides a rigorous, multi-dimensional analysis of verification dynamics in LLMs, establishing that verification success is governed by the interaction of problem difficulty, generator capability, and verifier generation capability. The results have direct implications for the deployment of verification in TTS, enabling more cost-effective and reliable model evaluation. The identification of regimes where scaling verifier capacity is ineffective underscores the need for principled, context-aware verification strategies and motivates further research into overcoming the fundamental limitations of current approaches.