Accurate and Efficient Low-Rank Model Merging in Core Space (2509.17786v1)

Abstract: In this paper, we address the challenges associated with merging low-rank adaptations of large neural networks. With the rise of parameter-efficient adaptation techniques, such as Low-Rank Adaptation (LoRA), model fine-tuning has become more accessible. While fine-tuning models with LoRA is highly efficient, existing merging methods often sacrifice this efficiency by merging fully-sized weight matrices. We propose the Core Space merging framework, which enables the merging of LoRA-adapted models within a common alignment basis, thereby preserving the efficiency of low-rank adaptation while substantially improving accuracy across tasks. We further provide a formal proof that projection into Core Space ensures no loss of information and provide a complexity analysis showing the efficiency gains. Extensive empirical results demonstrate that Core Space significantly improves existing merging techniques and achieves state-of-the-art results on both vision and language tasks while utilizing a fraction of the computational resources. Codebase is available at https://github.com/apanariello4/core-space-merging.

• The paper proposes Core Space Merging, an approach that projects LoRA updates into a shared low-rank subspace for efficient, lossless integration.
• It uses SVD on stacked adaptation matrices to create reference bases, ensuring zero alignment error for linear merging functions.
• Empirical results show up to 600× speedup and superior accuracy across vision and language tasks compared to full-space and KnOTS methods.

Accurate and Efficient Low-Rank Model Merging in Core Space

Introduction and Motivation

The proliferation of large-scale neural architectures has driven the adoption of parameter-efficient fine-tuning (PEFT) methods, such as Low-Rank Adaptation (LoRA), to mitigate the prohibitive costs of full-model adaptation. While LoRA enables efficient specialization of large models for diverse tasks, the challenge of merging multiple LoRA-adapted experts into a single, multi-task model remains unresolved. Existing merging strategies either operate in the full parameter space—negating the efficiency of LoRA—or in alignment spaces that require expensive decompositions, such as KnOTS, which scale poorly with model size. This work introduces Core Space Merging, a framework that enables accurate and efficient merging of LoRA-adapted models by projecting updates into a shared, information-preserving low-rank subspace.

Core Space Merging: Theoretical Framework

The central contribution is the definition and construction of the Core Space, a compact subspace that supports arbitrary merging strategies while retaining the low-rank structure of LoRA. For each task $t$, LoRA updates are parameterized as $\Delta W^{(t)} = B^{(t)}A^{(t)}$, with $A^{(t)} \in \mathbb{R}^{r \times n}$ and $B^{(t)} \in \mathbb{R}^{m \times r}$, $r \ll \min(m, n)$. The key insight is to perform SVD on the stacked $A^{(t)}$ and $B^{(t)}$ matrices across all tasks, yielding reference bases $A$ and $B$ that span the union of all task subspaces.

Each task's update is then projected into this shared basis, resulting in a core matrix $M^{(t)}$ of size $r \times r$. Alignment between task-specific and reference bases is achieved via least-squares solutions, ensuring that the projection and reconstruction are lossless. Merging is performed in the core space, and the merged update is mapped back to the original parameter space via the reference bases.

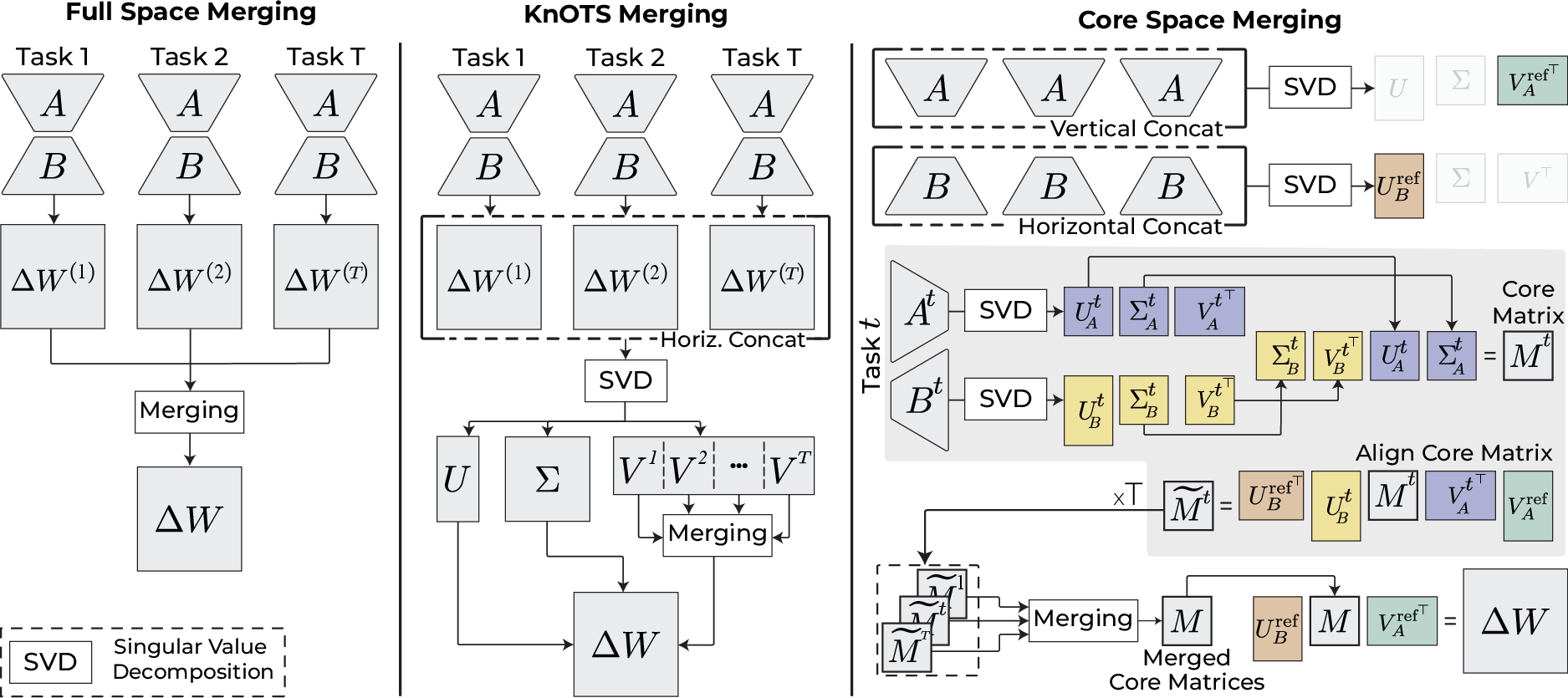
Figure 1: Full Space Merging reconstructs full matrices for merging, KnOTS merges in a costly alignment space, while Core Space Merging operates efficiently in a compact, shared subspace.

Theoretical analysis demonstrates that this procedure incurs zero alignment error: the transformation to and from core space is exactly invertible, and the merged model is identical to that obtained by merging in the full space for linear merging functions (e.g., Task Arithmetic). For non-linear merging strategies, empirical results show that core space merging yields superior performance.

Computational Efficiency

A critical advantage of Core Space Merging is its computational scalability. The dimensionality of the core space depends only on the number of tasks $T$ and the LoRA rank $r$, not on the base model size. Complexity analysis reveals that, for $T, r \ll n$, the dominant cost is $\mathcal{O}(n^2 T r)$, which is orders of magnitude lower than the cubic or super-cubic costs of KnOTS and full-space SVD-based methods.

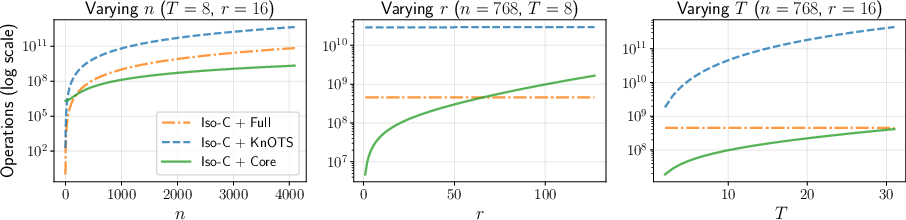
Figure 2: Core Space merging achieves efficiency comparable to full space merging, but with much higher accuracy, and is dramatically more efficient than KnOTS as the number of tasks increases.

This efficiency enables the application of sophisticated merging strategies, such as Iso-C and TSV, to large models (e.g., Llama 3 8B) that would otherwise be computationally infeasible.

Empirical Results

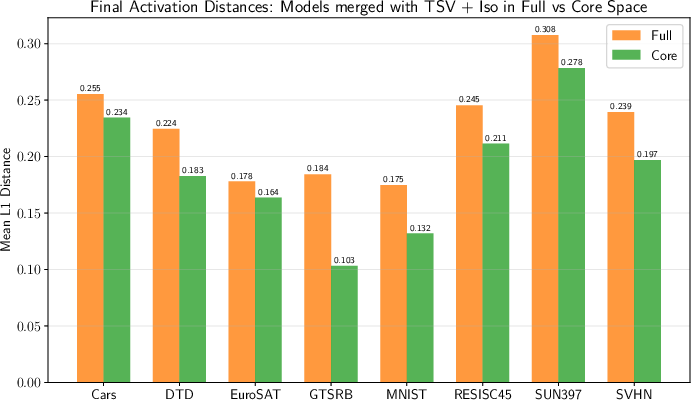
Extensive experiments are conducted on both vision (ViT-B/32, ViT-L/14) and language (Llama 3 8B) backbones, using LoRA-adapted models fine-tuned on multiple tasks. Core Space Merging is evaluated against full space and KnOTS merging, using a suite of merging strategies: Task Arithmetic (TA), TIES, DARE, TSV, CART, and Iso-C.

Key empirical findings:

• State-of-the-art accuracy: Core Space Merging consistently achieves the highest normalized accuracy across all tested merging strategies and tasks, outperforming both full space and KnOTS.
• Dramatic speedup: For Llama 3 8B, Core Space Merging provides up to $600\times$ speedup over KnOTS for Iso-C, with no loss in accuracy.
• Robustness to heterogeneous ranks: The method seamlessly supports merging LoRA modules with different ranks, maintaining performance advantages.
• Generalization to other PEFT methods: The framework extends to VeRA and other low-rank adaptation schemes by absorbing scaling vectors into the low-rank matrices.

Analysis of Core Space Properties

The information density and alignment properties of the core space are analyzed:

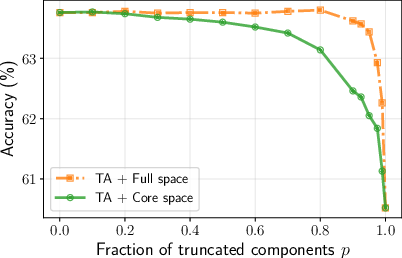
Figure 3: Truncation of components in full space has little effect, but any truncation in core space causes a sharp performance drop, indicating that core space is information-dense.

• Information density: Truncation experiments show that the core space is highly information-dense; removing any component leads to a significant drop in performance, unlike the full space, which contains many redundant directions.
• Subspace alignment: The Subspace Alignment Ratio (SAR) between task updates is significantly higher in core space, indicating that the shared basis enforces better alignment and reduces destructive interference during merging.

  Figure 4: Mean L1 distance between task-specific and merged model embeddings is lower in core space, indicating reduced interference and better knowledge integration.

Implementation and Practical Considerations

The core space merging algorithm is straightforward to implement and is compatible with any merging strategy that operates on weight matrices. The optimized implementation avoids explicit SVDs of each LoRA matrix, instead projecting directly via the reference bases. The method is robust to overcomplete settings ($T \cdot r > m, n$), and the theoretical guarantees of lossless reconstruction hold in all cases.

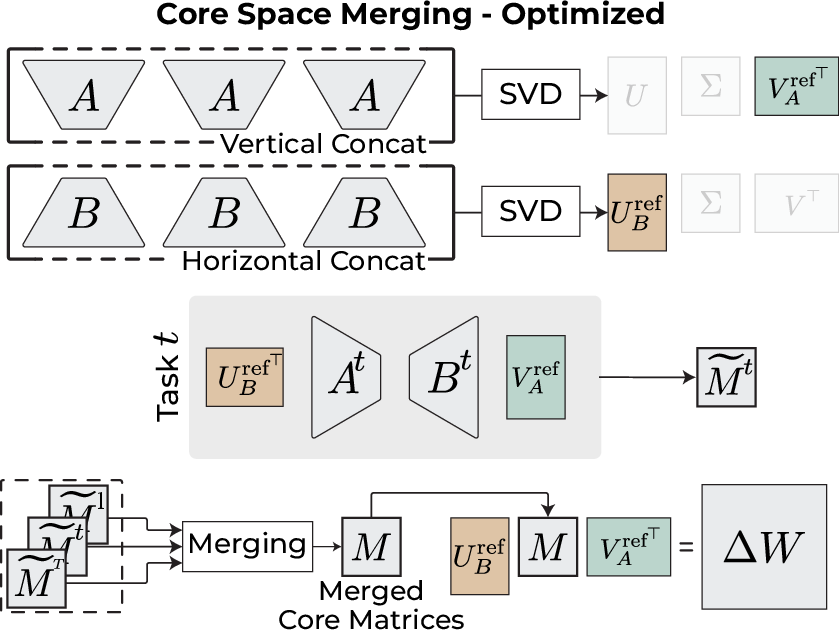
Figure 5: The optimized Core Space Merging pipeline: SVD on stacked low-dimensional matrices yields reference bases, followed by direct computation of aligned core matrices and efficient merging.

Implications and Future Directions

The Core Space Merging framework addresses a critical bottleneck in scalable multi-task adaptation of large models. By enabling efficient, accurate, and information-preserving merging of LoRA-adapted experts, it facilitates collaborative model development, federated learning, and rapid composition of specialized capabilities. The method's generality suggests applicability to a broad class of low-rank adaptation techniques and opens avenues for further research in:

• Dynamic subspace selection: Adapting the core space dimensionality based on task similarity or data-driven criteria.
• Federated and continual learning: Efficiently aggregating updates from distributed or sequentially arriving tasks.
• Extension to structured and sparse adaptation methods: Generalizing the framework to other forms of parameter-efficient adaptation.

Conclusion

Core Space Merging provides a theoretically sound and practically efficient solution for merging LoRA-adapted models. By projecting updates into a shared, information-dense subspace, it achieves state-of-the-art accuracy and scalability across vision and language domains. The framework's efficiency and extensibility position it as a foundational tool for multi-task adaptation and collaborative model development in large-scale neural architectures.