Hierarchical Retrieval: The Geometry and a Pretrain-Finetune Recipe (2509.16411v1)
Abstract: Dual encoder (DE) models, where a pair of matching query and document are embedded into similar vector representations, are widely used in information retrieval due to their simplicity and scalability. However, the Euclidean geometry of the embedding space limits the expressive power of DEs, which may compromise their quality. This paper investigates such limitations in the context of hierarchical retrieval (HR), where the document set has a hierarchical structure and the matching documents for a query are all of its ancestors. We first prove that DEs are feasible for HR as long as the embedding dimension is linear in the depth of the hierarchy and logarithmic in the number of documents. Then we study the problem of learning such embeddings in a standard retrieval setup where DEs are trained on samples of matching query and document pairs. Our experiments reveal a lost-in-the-long-distance phenomenon, where retrieval accuracy degrades for documents further away in the hierarchy. To address this, we introduce a pretrain-finetune recipe that significantly improves long-distance retrieval without sacrificing performance on closer documents. We experiment on a realistic hierarchy from WordNet for retrieving documents at various levels of abstraction, and show that pretrain-finetune boosts the recall on long-distance pairs from 19% to 76%. Finally, we demonstrate that our method improves retrieval of relevant products on a shopping queries dataset.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about making search systems smarter when the things you search for are organized in levels, like a family tree or a set of categories. The authors paper “Hierarchical Retrieval,” where the goal isn’t just to find the exact item that matches a query, but also to find all more general items above it in a hierarchy (its “ancestors”). They show that a simple, fast kind of search model called a Dual Encoder can handle this kind of task, explain the math behind why it works, and provide a practical training recipe that fixes a common problem: the model struggles to find items that are far up the hierarchy (the “lost-in-the-long-distance” issue). They test their ideas on WordNet (a big dictionary of word relationships) and a shopping search dataset, and see strong improvements.
Key Objectives and Questions
- Can Dual Encoders (DEs) even solve hierarchical retrieval? In other words, is it mathematically possible to embed queries and documents so that ancestors are correctly retrieved?
- If it’s possible, can we actually learn those embeddings from normal training data?
- Why do DEs tend to miss far-away ancestors, and how can we fix that without harming performance on close (nearby) matches?
Methods and Approach
What is a Dual Encoder (DE)?
- A Dual Encoder turns queries (like “kid’s sandals”) and documents (like product titles or word concepts) into numbers (vectors) in the same space.
- If a query and a document are similar, their vectors should point in similar directions or sit close together.
- The model learns two encoders: one for queries and one for documents. This is useful when relevance is one-way. For example, “Sandals” is relevant to “Kid’s sandals,” but “Kid’s sandals” is not relevant to “Sandals” (too specific). Having two encoders helps capture this asymmetry.
What is Hierarchical Retrieval?
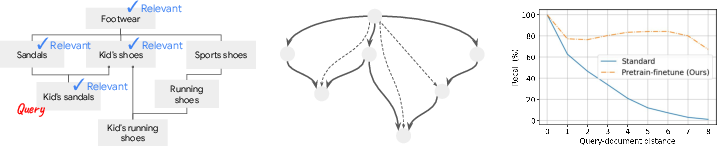
- Imagine a tree of concepts: “Footwear” at the top, then “Shoes,” then “Sandals,” then “Kid’s sandals” near the bottom.
- Given a query for “Kid’s sandals,” the system should retrieve its ancestors: “Sandals,” “Shoes,” and “Footwear.”
- The hierarchy can be represented by a directed acyclic graph (DAG), which is just a graph with arrows pointing from a child to its parent and no loops.
Geometry: Is DE feasible for hierarchies?
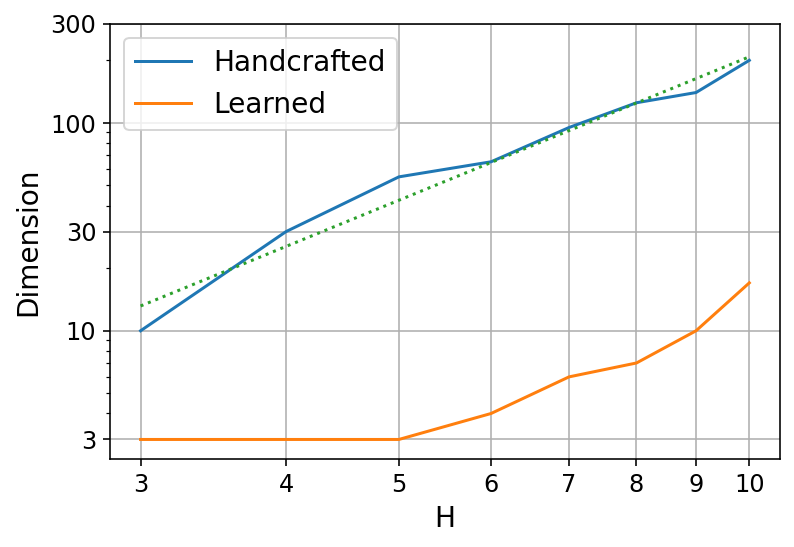
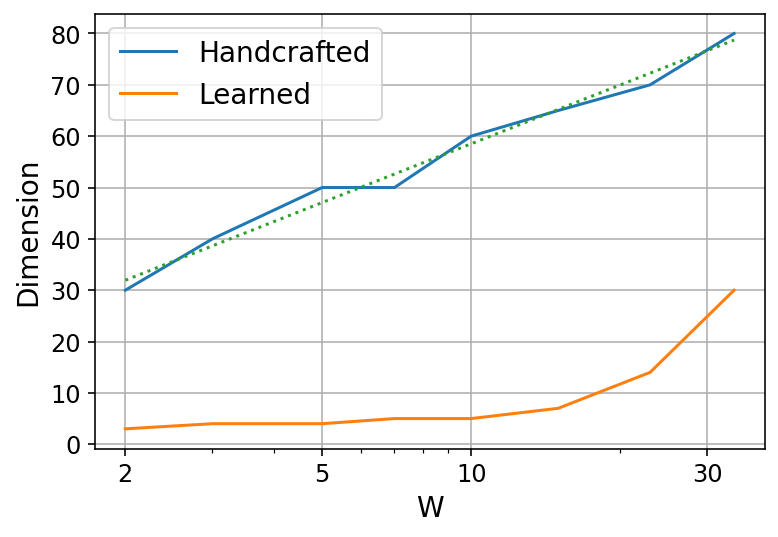
- The authors prove that it is possible to place all query and document vectors so that relevant (ancestor) documents have higher similarity than irrelevant ones.
- You need enough “space” (embedding dimension) to do this. The required dimension grows:
- Linearly with the depth of the hierarchy (how many levels up you need to retrieve).
- Only logarithmically with the number of documents (so even millions of documents can fit into a fairly small dimension).
- They give a constructive method: randomly place document vectors, then build each query vector as a combination of its matching documents’ vectors. With enough dimensions, this reliably separates relevant from irrelevant documents.
Learning from data: Does standard training work?
- In practice, you don’t know the full hierarchy. You train on examples of query-document pairs that should match.
- They train DEs using a typical loss (softmax + cross-entropy) that encourages correct pairs to have higher similarity than others.
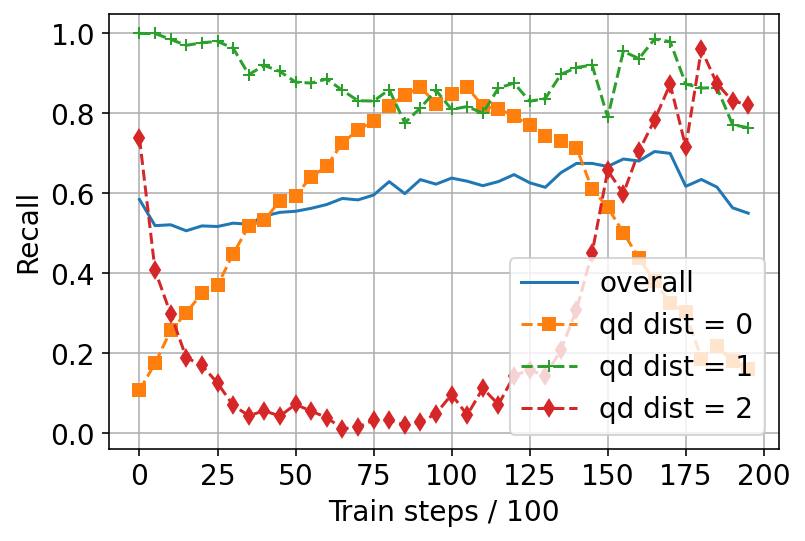
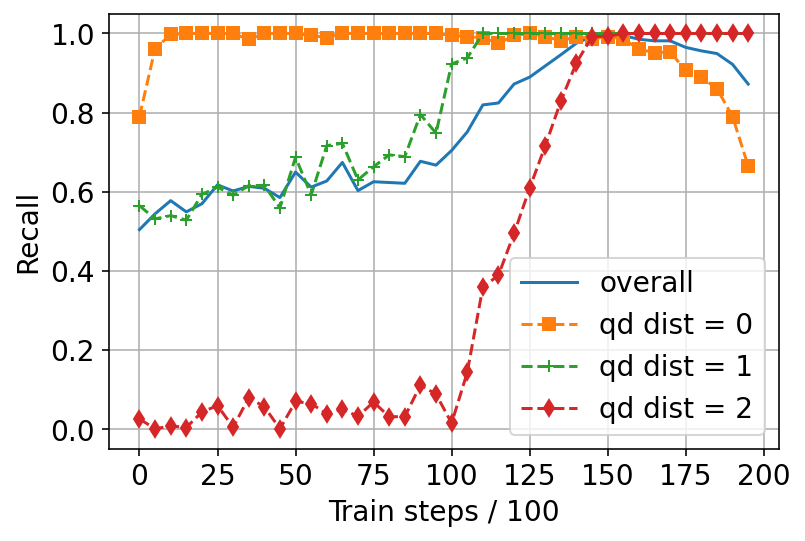
A common problem: “Lost-in-the-long-distance”
- When embeddings are small (few dimensions), DEs tend to do great on close matches (like exact matches or direct parents) but miss far ancestors (higher levels in the hierarchy).
- A naive fix is to oversample long-distance pairs during training. This helps those long-distance cases but hurts performance on short-distance ones—so it just shifts the problem.
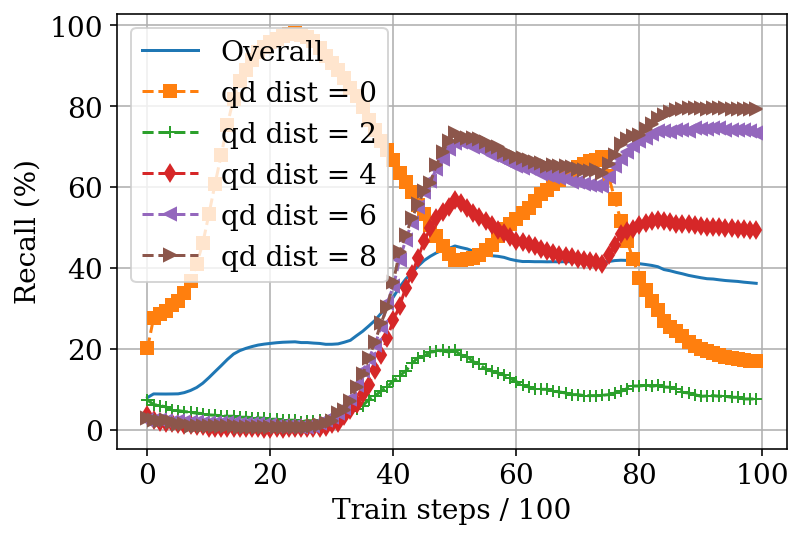
The fix: Pretrain–Finetune Recipe
- Pretrain: Train the DE on regular data (which mostly includes close matches). This establishes a strong base.
- Finetune: Then continue training only on long-distance matches. This boosts the model’s ability to retrieve far ancestors without erasing what it learned about close ones.
- In practice, they also adjust training settings (like learning rate and temperature) during finetuning to stabilize learning.
Main Findings and Why They Matter
- DEs are theoretically capable of hierarchical retrieval. The math shows you can separate relevant ancestors from others with modest embedding sizes, even for very large document sets.
- DEs can be learned from normal training data. In synthetic (simulated) hierarchies, standard training finds good solutions when the embedding dimension is large enough.
- In low dimensions, models miss far-away ancestors. This is the “lost-in-the-long-distance” phenomenon: accuracy drops for documents several steps up the hierarchy.
- Pretrain–Finetune dramatically improves long-distance retrieval:
- On WordNet (a hierarchy of English word concepts), the recall for very long-distance matches jumps from about 19% to about 76% with the recipe (while keeping near distances strong).
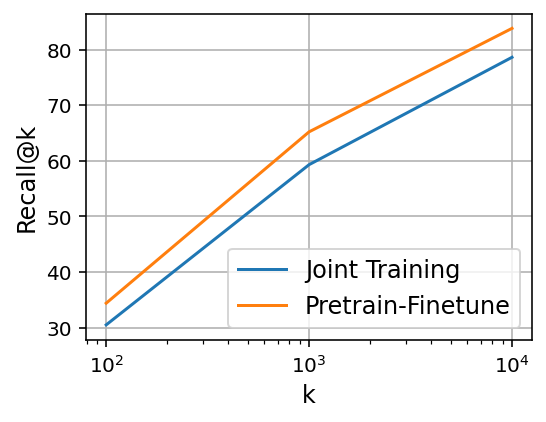
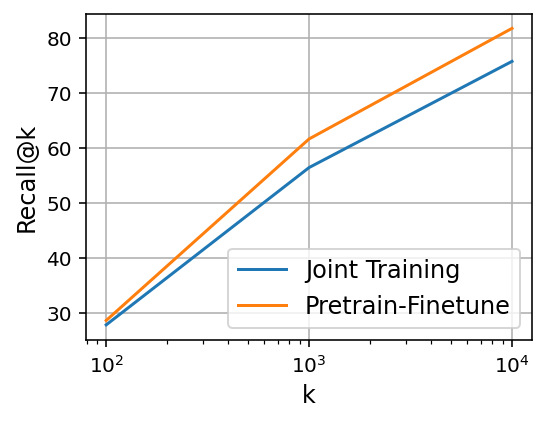
- On a shopping search dataset (ESCI), a single DE trained with the recipe retrieves both exact matches and more general “substitute” matches better than training them jointly from scratch.
Why it’s important:
- Real-world search often involves hierarchies: categories in online stores, topic trees in knowledge bases, and word relationships in language.
- Fast, scalable models like DEs are widely used in industry. Proving they can handle hierarchies and showing a simple training trick to fix their blind spots helps make practical systems better without expensive changes.
Implications and Impact
- Better ad and product search: The model can retrieve not only the exact target but also appropriate, more general options (ancestors), which supports features like “phrase match” or broader category targeting.
- Stronger language understanding: Improved retrieval of hypernyms (more general word concepts) helps tasks that rely on understanding abstraction and hierarchy.
- Practical recipe: Pretrain–Finetune is easy to apply. You don’t need the full hierarchy; you only need a way to identify or approximate “long-distance” pairs (e.g., substitute matches vs exact matches).
- Efficiency: The required embedding dimension scales gently (logarithmically) with the number of documents, making it feasible for very large databases.
In short, the paper shows that Dual Encoders can handle hierarchical retrieval both in theory and practice, identifies a key failure mode, and offers a simple, effective training recipe to fix it—leading to better search across many real-world, hierarchical settings.
Knowledge Gaps
Knowledge Gaps, Limitations, and Open Questions
Below is a focused list of concrete gaps and open problems that remain unresolved, intended to guide actionable follow-up research.
- Tightness of the embedding-dimension bounds
- No lower bounds: The paper proves feasibility with but provides no matching lower bounds; it is unknown whether these rates (and constants) are tight for general DAGs or specific families (trees, lattices, DAGs with high in-degree).
- Dependence beyond s: The bound depends only on the maximum number of relevant documents per query (). It remains unclear how other graph properties (e.g., width/profile, maximum in/out-degree, longest antichain, number of parents per node, local curvature of partial order) affect the necessary dimension.
- Worst-case DAGs: For DAGs where approaches , the bound becomes vacuous; characterizing which realistic hierarchies yield favorable vs. unfavorable dimensional requirements is open.
- From existence to learnability guarantees
- Sample complexity: No theoretical guarantees on the number of training pairs needed (as a function of , , depth, noise) for the batch-softmax objective to learn HR-capable embeddings.
- Optimization theory: No analysis of convergence or implicit bias of the softmax/in-batch negative objective for asymmetric HR, nor conditions under which gradient-based training recovers the geometric separation promised by the construction.
- Generalization to arbitrary DAGs: Learning results are demonstrated on trees and WordNet; learning behavior and guarantees for general DAGs with multiple parents and cycles eliminated remain unexplored.
- Formal understanding of the lost-in-the-long-distance phenomenon
- Mechanistic cause: The paper documents the effect empirically but does not explain its cause (e.g., gradient signal dilution with increasing path length, bias induced by negative sampling, temperature/normalization effects, embedding curvature limits).
- Predictive diagnostics: No metrics or training-time signals (e.g., margin statistics by distance, per-level gradient norms) to detect the onset or severity of long-distance failures.
- Theoretical model: No formal model linking distance distribution, objective temperature, and sampling strategy to expected recall by distance.
- Pretrain-finetune recipe: scope, robustness, and theory
- Theoretical justification: Why does two-stage optimization avoid the trade-off observed with single-stage rebalancing? A formal argument (e.g., loss landscape smoothing, basin hopping, or representation anchoring) is missing.
- Scheduling sensitivity: The approach relies on early stopping and a large temperature during finetuning; there is no principled method to choose schedule length, temperature, and learning rates or to guarantee no catastrophic forgetting.
- Proxy definition of “long distance”: The method presumes access to a proxy partition of pairs into short vs. long distance; systematic procedures to construct such proxies (without a DAG) and quantify their quality and bias are lacking.
- Sample efficiency: Minimum amount and quality of long-distance data required for effective finetuning—and sensitivity to label noise—are not characterized.
- Unification with curriculum or multi-task training: It remains open whether adaptive curricula, dynamic sampling, or multi-task objectives can match or surpass two-stage training without forgetting.
- Practical retrieval and deployment considerations
- Unknown k at inference: Evaluation uses Recall@|S(q)|; in practice |S(q)| is unknown. Methods for thresholding, calibrating scores, or predicting cutoffs per query are not studied.
- Precision–recall trade-offs: The work emphasizes recall; precision, PR/AUC, and downstream business metrics (e.g., CTR for advertising) by distance slice are not assessed.
- ANN indexing effects: Impact of approximate nearest neighbor search (quantization, HNSW parameters), index-time compression, and latency/memory constraints on long-distance recall is not evaluated.
- Stability under finetuning: How much do document embeddings move during finetuning (index drift), and what are the operational costs (re-indexing frequency, cache invalidation)?
- Modeling choices and alternatives left unexplored
- Baselines with non-Euclidean/structured embeddings: No side-by-side retrieval evaluation against Poincaré, box/ball/order embeddings, probabilistic embeddings, or graph neural approaches that explicitly encode asymmetry/transitivity.
- Alternative losses and samplers: The paper uses batch-softmax with in-batch negatives; the effects of margin/circle/listwise losses, hard negative mining, temperature schedules, class-balanced/focal losses, and hierarchical-aware negatives are unexplored.
- Encoder asymmetry and sharing: The impact of tying vs. separating query/document encoders, normalization (cosine vs. dot product), and architectural choices (e.g., biaffine heads) on long-distance retrieval is unstudied.
- Multi-positive/listwise training: HR has multiple positives per query; dedicated multi-positive or listwise objectives could be beneficial but were not evaluated.
- Data and labeling assumptions
- Exact-match assumption: The HR definition assumes each query has an exact document match; in real systems many queries lack exact matches or are out-of-distribution. Methods to handle such cases (e.g., abstention, generative query expansion) are not considered.
- Uniform relevance across ancestors: All ancestors are treated as equally relevant; in practice, relevance may decay with distance. Distance-aware weighting or gains for ranking are not incorporated or evaluated.
- Noisy/partial hierarchies: Robustness to noisy relevance labels, partial DAGs, or conflicting parentage is not analyzed; the constructive theory assumes correct S(q) sets.
- Scope and external validity of experiments
- Beyond WordNet/ESCI: Generalization to other domains (e.g., legal, medical ontologies), languages, and deeper/wider or denser DAGs remains untested.
- Textual generalization: WordNet experiments use lookup-table embeddings; transfer to natural-language encoders on unseen queries and long-tail terminology is not demonstrated.
- Scale and dimension regimes: Industrial DEs often use higher dimensions (e.g., 128–768); the trade-offs between dimension, recall by distance, and index cost at realistic scales (108–109) are not profiled.
- Evaluation methodology and diagnostics
- Slice-aware monitoring: No standardized suite to monitor recall/precision by distance during training/finetuning; actionable diagnostics for early stopping or schedule adaptation are absent.
- Error analysis: Limited qualitative analysis; no taxonomy of failure types (e.g., sibling confusions vs. skipping multiple levels) to guide targeted improvements.
- Extensions of the theory to noisy or approximate HR
- Noise-tolerant guarantees: The constructive result is exact; conditions under which approximate separation (with bounded false negatives/positives) is guaranteed under label noise or missing pairs are not studied.
- Per-query thresholds: The theorem uses a universal threshold r; whether per-query thresholds reduce dimension requirements or improve robustness is an open question.
- Combining DE with structured or re-ranking components
- Hybrid pipelines: Potential gains from adding a cross-encoder re-ranker or a lightweight graph-aware post-processor to recover long-distance misses are not investigated.
- Semi-supervised graph augmentation: Using partial hierarchy knowledge, self-training, or random-walk pretraining to improve long-distance recall is not explored.
- Operational risks and maintenance
- Continual learning: How to maintain long-distance recall under distribution shift or incremental index changes (add/delete documents) without repeated two-stage training is unclear.
- Catastrophic forgetting controls: Mechanisms such as regularization, EWC, or rehearsal during finetuning to prevent short-distance degradation beyond early stopping are not examined.
Each of these points suggests concrete follow-up work, ranging from theoretical analyses (lower bounds, noise tolerance, optimization dynamics) to practical algorithmic exploration (alternative objectives, baselines, curriculum design), evaluation expansions (distance-sliced precision/recall, ANN effects), and deployment-focused studies (thresholding, stability, continual learning).
Glossary
- approximate nearest neighbor search: Algorithms that quickly retrieve items with vectors near a query vector in large-scale embedding spaces. "approximate nearest neighbor search"
- asymmetric DEs: Dual encoder setups where query and document embeddings are produced by different encoders, allowing non-symmetric relevance. "asymmetric DEs"
- cross-entropy loss: A standard loss function measuring the difference between predicted probabilities and true labels in classification. "cross-entropy loss"
- directed acyclic graph (DAG): A directed graph with no cycles, used here to represent hierarchical relations among documents. "directed acyclic graph (DAG)"
- document encoder: The component of a dual encoder that maps documents into vectors in an embedding space. "document encoder"
- Dual Encoder (DE): A retrieval architecture with separate encoders for queries and documents whose embeddings are compared via a similarity measure. "Dual Encoder (DE)"
- embedding dimension: The number of coordinates in the vector representation produced by an encoder. "embedding dimension"
- ESCI: A public shopping queries dataset with labeled query–product relevance categories used for retrieval evaluation. "ESCI"
- Exact: In ESCI, a relevance label indicating the product fully satisfies the query’s specifications. "Exact"
- Euclidean geometry: The standard geometric structure of vector spaces where distances and angles follow Euclidean rules, impacting how embeddings can represent hierarchy. "Euclidean geometry"
- finetuning: A training stage where a pretrained model is further trained on a targeted dataset to improve performance on a specific aspect. "finetuning"
- Heavy-Tail sampling: A data sampling scheme that up-samples long-distance or rarer pairs to rebalance training data. "Heavy-Tail sampling"
- Hierarchical Retrieval (HR): Retrieval where documents are organized in a hierarchy and relevant items include ancestors of a query’s exact match. "Hierarchical Retrieval (HR)"
- HyperLex: A benchmark for evaluating models on hyponymy–hypernymy relations between concept pairs. "HyperLex"
- hypernym: A word denoting a more general concept in a hierarchy (e.g., animal is a hypernym of cat). "hypernym"
- inner product: A similarity measure between query and document embeddings computed as the dot product. "inner product"
- Lazy Adam optimizer: An optimization algorithm variant used for training large sparse models or embeddings efficiently. "Lazy Adam optimizer"
- lookup-table DE: A dual encoder where each query/document has a directly learned embedding vector stored in a table. "lookup-table DE"
- lost-in-the-long-distance phenomenon: The degradation in retrieval accuracy for matches that are farther apart in the hierarchy. "lost-in-the-long-distance phenomenon"
- Phrase Match: An ad-targeting notion where relevant keywords are semantically more general than the user’s query. "Phrase Match"
- pretrain-finetune recipe: A training approach that first learns general representations, then specializes on targeted data (e.g., long-distance pairs). "pretrain-finetune recipe"
- Query-document distance: The number of hierarchical steps between a query’s node and a matching document’s node. "Query-document distance"
- query encoder: The component of a dual encoder that maps queries into vectors in an embedding space. "query encoder"
- recall@k: The fraction of relevant items that appear among the top-k retrieved results for each query. "recall@k"
- softmax loss: A learning objective using softmax-normalized scores to train models to rank correct matches higher than negatives. "softmax loss"
- Spearman correlation: A nonparametric rank correlation metric used to evaluate how well model scores align with human judgments. "Spearman correlation score"
- temperature: A scaling parameter in softmax-based training that controls the sharpness of the probability distribution over scores. "temperature"
- Transformers: Neural network architectures based on self-attention, used here as encoders for queries and documents. "Transformers"
- WordNet: A large lexical database organizing English words into synsets with semantic relations such as hypernymy. "WordNet"
Collections
Sign up for free to add this paper to one or more collections.