DiffusionNFT: Online Diffusion Reinforcement with Forward Process (2509.16117v1)
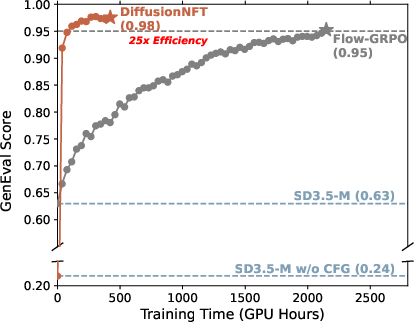
Abstract: Online reinforcement learning (RL) has been central to post-training LLMs, but its extension to diffusion models remains challenging due to intractable likelihoods. Recent works discretize the reverse sampling process to enable GRPO-style training, yet they inherit fundamental drawbacks, including solver restrictions, forward-reverse inconsistency, and complicated integration with classifier-free guidance (CFG). We introduce Diffusion Negative-aware FineTuning (DiffusionNFT), a new online RL paradigm that optimizes diffusion models directly on the forward process via flow matching. DiffusionNFT contrasts positive and negative generations to define an implicit policy improvement direction, naturally incorporating reinforcement signals into the supervised learning objective. This formulation enables training with arbitrary black-box solvers, eliminates the need for likelihood estimation, and requires only clean images rather than sampling trajectories for policy optimization. DiffusionNFT is up to $25\times$ more efficient than FlowGRPO in head-to-head comparisons, while being CFG-free. For instance, DiffusionNFT improves the GenEval score from 0.24 to 0.98 within 1k steps, while FlowGRPO achieves 0.95 with over 5k steps and additional CFG employment. By leveraging multiple reward models, DiffusionNFT significantly boosts the performance of SD3.5-Medium in every benchmark tested.
Summary
- The paper introduces DiffusionNFT, a reinforcement learning method that optimizes the forward diffusion process using negative-aware finetuning.
- The approach eliminates the need for likelihood estimation and CFG, enabling flexible integration with arbitrary black-box solvers.
- Experiments demonstrate that DiffusionNFT achieves superior performance and efficiency in both in-domain and out-of-domain tasks compared to traditional methods.
DiffusionNFT: Online Diffusion Reinforcement with Forward Process
The paper "DiffusionNFT: Online Diffusion Reinforcement with Forward Process" introduces a novel approach to reinforcement learning (RL) for diffusion models, addressing the challenges posed by intractable likelihoods in these models. The proposed method, Diffusion Negative-aware FineTuning (DiffusionNFT), optimizes diffusion models directly on the forward process, contrasting positive and negative generations to define an implicit policy improvement direction. This approach integrates reinforcement signals into the supervised learning objective, enabling efficient training without the need for likelihood estimation or Classifier-Free Guidance (CFG).
Introduction
Diffusion models have become a cornerstone in visual generation tasks, yet extending RL techniques to these models has been challenging due to the difficulty in computing exact likelihoods. Traditional RL methods, such as GRPO, discretize the reverse sampling process, treating diffusion generation as a multi-step decision-making problem. However, this approach suffers from several limitations, including forward-reverse inconsistency, solver restrictions, and complex CFG integration.
DiffusionNFT addresses these issues by focusing on the forward diffusion process, leveraging flow matching to optimize policy directly. This method contrasts positive and negative samples to define a policy improvement direction, allowing for training with arbitrary black-box solvers and eliminating the need for sampling trajectories.
Figure 1: Performance of DiffusionNFT compared to FlowGRPO, highlighting efficiency and CFG-free operation.
Methodology
Diffusion Reinforcement via Negative-aware Finetuning
DiffusionNFT introduces a new RL paradigm that operates on the forward diffusion process. The method defines an improvement direction between positive and negative policies, integrating reinforcement guidance directly into the optimized policy. This approach offers several advantages:
- Forward Consistency: By focusing on the forward process, DiffusionNFT maintains adherence to the Fokker-Planck equation, ensuring the model corresponds to a valid forward process.
- Solver Flexibility: The decoupling of policy training and data sampling allows the use of any black-box solvers, enhancing generation efficiency.
- Implicit Guidance Integration: DiffusionNFT employs an implicit parameterization technique, integrating reinforcement guidance directly into the learned policy without the need for separate guidance models.
- Likelihood-Free Formulation: The method bypasses the need for likelihood estimation, avoiding systematic estimation bias.
Figure 2: Comparison between Forward-Process RL (NFT) and Reverse-Process RL (GRPO), showcasing solver flexibility and trajectory-free optimization.
Practical Implementation
DiffusionNFT is implemented through a series of steps involving data collection, policy optimization, and soft updates. The algorithm leverages optimality rewards, adaptive loss weighting, and CFG-free optimization to enhance training stability and efficiency.
1 2 3 4 5 6 7 8 9 10 11 |
def diffusionNFT(training_policy, data_collection_policy, reward_function, prompt_dataset): for iteration in range(num_iterations): for prompt in prompt_dataset: images, rewards = collect_data(prompt, data_collection_policy) normalized_rewards = normalize_rewards(rewards) update_data_buffer(images, normalized_rewards) for batch in data_buffer: optimize_policy(batch, training_policy) update_data_collection_policy(training_policy) |
Experiments
Multi-Reward Joint Training
DiffusionNFT demonstrates strong performance across multiple rewards, surpassing CFG-based models and matching FlowGRPO in both in-domain and out-of-domain metrics. The method efficiently optimizes the base model, achieving superior visual quality.
Head-to-Head Comparison
In single-reward settings, DiffusionNFT exhibits significant efficiency improvements over FlowGRPO, achieving better scores in fewer iterations.
Figure 3: Head-to-head comparison between DiffusionNFT and FlowGRPO on single rewards.
Ablation Studies
The paper conducts ablation studies to analyze the impact of core design choices, such as negative loss, diffusion sampler, adaptive weighting, soft update strategies, and guidance strength.
Figure 4: Different diffusion samplers for data collection.
Conclusion
DiffusionNFT represents a significant advancement in the RL domain for diffusion models, offering a scalable, efficient, and theoretically principled approach. By focusing on the forward process, the method provides a unified framework for integrating supervised and reinforcement learning in diffusion models, paving the way for future developments in AI.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Explain it Like I'm 14
Easy-to-Read Summary of “DiffusionNFT: Online Diffusion Reinforcement with Forward Process”
What is this paper about?
This paper introduces a new way to improve image‑generating AI models called diffusion models. The new method is named DiffusionNFT. It helps the model learn from feedback (like a coach giving a score to each image) while it is still being used (“online” learning). The key idea is to train on the simple “forward” part of diffusion (adding noise) instead of the complicated “reverse” part (removing noise). This makes training faster, simpler, and more flexible.
What questions does the paper ask?
The paper focuses on three main questions:
- Can we do reinforcement learning (RL) for diffusion models by training on the forward process (adding noise), not the reverse process (removing noise)?
- Can we use both good and bad generations to guide the model in the right direction?
- Can we avoid tricky math like exact likelihoods and avoid extra tricks like CFG (Classifier-Free Guidance), yet still get better and faster results?
How does the method work? (Using simple analogies)
Think of image generation like sculpting a statue from a noisy block of stone:
- The “forward process” is like covering a clean statue with layers of dust (adding noise).
- The “reverse process” is like carefully brushing away the dust to reveal the statue (denoising).
Most past RL methods tried to teach the model during the reverse process. That is hard, slow, and limits the tools you can use.
DiffusionNFT does something smarter:
- It generates several images for a given text prompt.
- A “judge” (a reward model) scores each image: higher score = better match to the goal.
- It splits the images into “positives” (good) and “negatives” (bad).
- Then it learns a direction to move the model from “what made bad images” toward “what made good images.” You can think of this as a compass pointing from “don’t do this” to “do more of that.”
How is this trained?
- Instead of adjusting the model during denoising (reverse), DiffusionNFT trains during the forward process using a standard technique called “flow matching.” In simple terms, the model learns how images change as noise is added, which also teaches it how to undo the noise later.
- The method uses an “implicit” trick so it doesn’t need two separate models (one for positives and one for negatives). It blends them inside one model using a single knob called the guidance strength (β). That keeps training simple and stable.
- It’s “off-policy,” which means it can learn from images made by older versions of the model—no need to tightly sync sampling and training.
- It only needs the final clean images (and their scores) for learning, not the whole step-by-step denoising path. This saves memory and time.
- You can use any sampler (any way of stepping through the process), including fast ODE solvers—no restriction to special noisy samplers.
In everyday language: DiffusionNFT treats feedback like a push from “bad” toward “good” and bakes that push directly into normal diffusion training, on the easier side of the process.
What did they find, and why is it important?
Key results:
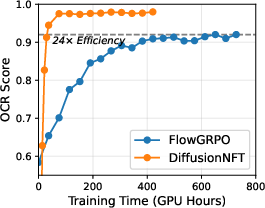
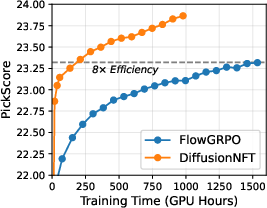
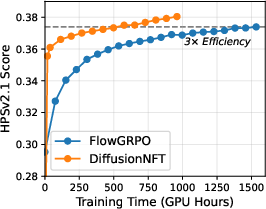
- Much faster learning: DiffusionNFT was 3× to 25× more efficient than a strong baseline called FlowGRPO.
- Big score jumps: On a test called GenEval, the score improved from 0.24 to 0.98 in about 1,000 steps. The baseline took over 5,000 steps to reach 0.95 and needed extra tricks (CFG).
- No CFG needed: DiffusionNFT trains a single model without CFG, yet still beats CFG-based baselines.
- Works with many goals at once: By combining multiple reward models (different “judges” that check different qualities like text alignment, image quality, readability of text in images, and human preference), the method significantly improved a popular base model (SD3.5-Medium) on all tested benchmarks.
- Practical tips:
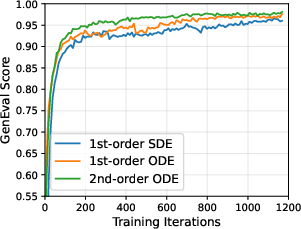
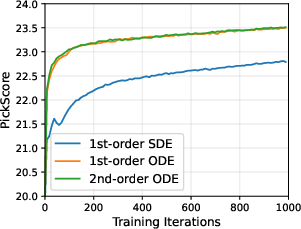
- Using ODE samplers generally gave better data for learning than SDE samplers.
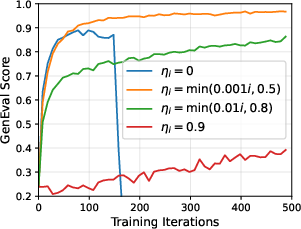
- The “negative-aware” part (penalizing bad generations) was crucial—removing it made training collapse.
- A careful schedule for updating the sampling model (soft EMA updates) and a smart loss weighting made training more stable.
- The guidance strength (β) balances speed and stability; values around 1 worked well.
Why this matters:
- Training on the forward process avoids many headaches (no need for exact likelihoods or storing long denoising chains).
- You can plug in any solver you like when generating images.
- It unifies reinforcement-style feedback with ordinary supervised training, making the system both simple and powerful.
What’s the bigger impact?
- Simpler, faster alignment: DiffusionNFT offers an easy recipe to make image generators follow instructions and human preferences better—without relying on complicated extras like CFG.
- Scales to many goals: Because it supports multiple reward models, it can make models better at a range of skills at the same time (accuracy, aesthetics, text rendering, etc.).
- Broadly useful idea: The “negative-aware” forward-training idea could inspire similar approaches in other kinds of generative models (images, video, maybe even audio).
- Practical for real systems: Being “likelihood-free,” “off-policy,” and “solver-flexible” lowers the cost and complexity of improving models online—useful for companies and labs that want fast iteration.
In short: DiffusionNFT shows that teaching diffusion models using the easy side of the process (adding noise) and learning from both good and bad examples can make training much faster, simpler, and more effective—all while removing the need for complex tricks.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a focused list of what remains missing, uncertain, or unexplored in the paper that future work could concretely address:
- Finite-sample and finite-capacity guarantees: Theorems assume unlimited data and model capacity; formal convergence and improvement guarantees under realistic data, capacity, and optimization noise are not established.
- Practical estimation of α(t) and Δ: The key guidance relation depends on intractable densities (πt+/πtold) and idealized rewards; no method is provided to estimate α(t) or Δ from finite samples, nor to adapt the guidance strength β to match α(t).
- Calibration of optimality probability r: The transformation from raw rewards to r∈[0,1] via group normalization and clipping is heuristic; the impact of miscalibration on theory and training stability, and methods to calibrate or learn r, are not analyzed.
- Sensitivity to reward normalization choices: The method relies on per-prompt grouping (K images), Z normalization, clipping bounds; sensitivity studies and principled selection strategies for K and Z are missing.
- Off-policy training without importance sampling: The paper asserts off-policy sufficiency but provides no bias bounds; conditions under which drift between πold and πθ harms learning (and how to detect/mitigate it) are open.
- EMA schedule theory: EMA updates of the sampling policy stabilize training empirically, but no theoretical guidance or adaptive schemes are provided to tune ηi for stability vs. sample-efficiency.
- Negative-aware loss side effects: While necessary to avoid collapse, potential impacts on diversity, coverage, and mode-dropping are not quantified (e.g., no FID/KID/precision-recall diversity metrics).
- Reward hacking and overoptimization: The method optimizes learned/model-based rewards; analyses of reward gaming (e.g., CLIP/PickScore artifacts), robustness to noisy/misaligned reward models, and countermeasures are absent.
- Multi-reward composition: Joint optimization uses a fixed training sequence; there is no framework for resolving conflicting rewards, learning dynamic weights, or exploring Pareto fronts for multi-objective trade-offs.
- Robustness to solver mismatch: Data are collected with arbitrary solvers while training uses the forward objective; the effect of solver choice during rollout vs. inference (including stochastic vs. deterministic, order, step count) on stability and performance is underexplored.
- Forward consistency claim: The paper argues improved adherence to the forward process but lacks formal verification or diagnostics quantifying Fokker–Planck consistency before vs. after finetuning.
- Generalization beyond images: Applicability to video, audio, 3D, or conditional tasks with longer temporal credit assignment is not validated; it is unclear whether reverse-process-free optimization suffices in temporally extended domains.
- Scaling to high resolutions and larger models: Experiments center on SD3.5-Medium at 512×512; compute, memory, and stability at 1024+ resolutions and with 8–12B+ parameter models are untested.
- Fair, apples-to-apples baselines: Head-to-head comparisons mix CFG use, solver choices, and step counts; controlled studies holding these factors constant are needed to isolate algorithmic gains from configuration differences.
- Human evaluation: Improvements are judged via automatic metrics (including in-domain reward models); human preference studies are needed to verify true perceptual and alignment gains and detect regressions.
- Safety and content constraints: Effects on safety (e.g., toxicity, NSFW leakage) and controllability under safety constraints are not examined; integration with safety rewards or constraints is an open direction.
- Hyperparameterization of β: Only global β choices are explored; the benefits of time-dependent β(t), prompt- or reward-adaptive β, and principled selection criteria remain open.
- Time-weighting w(t) design: The adaptive self-normalized weighting is heuristic; its theoretical grounding, stability region, and interactions with solver order and step counts are not characterized.
- Pairwise preference integration: The method uses scalar rewards; extending NFT-style forward training to pairwise preference data (DPO-like objectives) with theoretical backing remains to be developed.
- CFG interplay and controllability: While the approach is CFG-free, many deployments desire controllable guidance; how to reintroduce or emulate CFG-like controls post-RL (without two-model complexity) is not addressed.
- Diversity–quality trade-offs under multi-reward training: Jointly optimizing alignment and aesthetic rewards could reduce diversity; explicit measurement and mitigation strategies (e.g., entropy regularization) are not provided.
- Sample complexity and compute accounting: Absolute sampling/training costs, memory footprints, replay buffer strategies, and cost-to-reward curves versus PPO/GRPO/RWR/DSPO-style baselines are not reported.
- Robustness to reward noise and drift: How the method behaves with noisy, drifting, or adversarial reward models (and how to regularize against them) is unexplored.
- Theoretical consistency under model misspecification: When vθ cannot represent the ideal target v*, the bias induced by implicit positive/negative parameterization and its impact on policy improvement remains unquantified.
- Applicability beyond LoRA: Results rely on LoRA finetuning; whether full-parameter tuning, adapters at different layers, or alternative parameter-efficient schemes affect stability, efficiency, or final performance is unknown.
- Data reuse and replay: The algorithm clears buffers each iteration; the benefits/risks of prioritized replay, longer-horizon off-policy reuse, and distributional coverage control are not studied.
- Long-prompt and compositional generalization: Beyond GenEval/OCR, performance on complex, long, compositional prompts, negative prompts, and fine-grained attribute control is not thoroughly evaluated.
- Inference-time efficiency/quality frontier: The influence of step count, solver order, and guidance strength on the quality–latency Pareto frontier, especially post-RL, is not systematically charted.
Glossary
- Adaptive Loss Weighting: A training strategy that adjusts the loss weight over diffusion time to stabilize or emphasize certain timesteps. "Adaptive Loss Weighting. Typical diffusion loss includes a time-dependent weighting w(t) (Eq.~\eqref{eq:diffusion_loss})."
- Black-box solvers: Sampling or integration methods treated as opaque procedures without needing internal gradients or structure. "First, DiffusionNFT allows data collection with arbitrary black-box solvers, rather than just first-order SDE samplers."
- Classifier-Free Guidance (CFG): An inference-time method that improves conditional generation by combining conditional and unconditional predictions. "Recent works discretize the reverse sampling process to enable GRPO-style training, yet they inherit fundamental drawbacks, including solver restrictions, forwardâreverse inconsistency, and complicated integration with classifier-free guidance (CFG)."
- DDIM: Denoising Diffusion Implicit Models; a non-stochastic sampling method for diffusion models derived from an ODE formulation. "This formulation is known as flow matching~\citep{lipman2022flow}, where simple Euler discretization serves as an effective ODE solver, equivalent to DDIM~\citep{song2020denoising}."
- Diffusion Negative-aware FineTuning (DiffusionNFT): An online RL approach for diffusion models that contrasts positive and negative samples on the forward process via flow matching. "We propose a new online RL paradigm: Diffusion Negative-aware FineTuning (DiffusionNFT)."
- Direct Preference Optimization (DPO): A preference-learning method that optimizes models from pairwise comparisons without explicit reward models. "Diffusion-DPO~\citep{wallace2024diffusion,yang2024using,liang2024step,yuan2024self, li2025divergence} adapts DPO to diffusion for paired human preference data but requires additional likelihood and loss approximations compared to AR."
- Energy guidance: A sampling-time guidance approach that uses an energy (score) function to steer diffusion generation. "Policy Guidance. This includes energy guidance \citep{diffuser, cep} and CFG-style guidance \citep{frans2025diffusion, jin2025inference}."
- Euler discretization: A first-order numerical method to integrate ODEs during reverse diffusion sampling. "This formulation is known as flow matching~\citep{lipman2022flow}, where simple Euler discretization serves as an effective ODE solver, equivalent to DDIM~\citep{song2020denoising}."
- Exponential Moving Average (EMA): A smoothing update rule that blends parameters over time for stability. "Instead, we leverage this property to employ a ``soft" EMA update:"
- Flow matching: Training via matching a model’s velocity field to the target data transport field along the diffusion time. "This formulation is known as flow matching~\citep{lipman2022flow}"
- Flow models: Generative models formulated as deterministic flows (ODEs) transporting noise to data. "While flow models naturally admit simple and efficient sampling through ODE, the lack of stochasticity hinders the application of GRPO."
- FlowGRPO: A GRPO-based RL method adapted for flow/diffusion models using an SDE formulation to reintroduce stochasticity. "FlowGRPO~\citep{liu2025flow} addresses this by using the SDE form~\citep{song2020score} under the velocity parameterization (see Appendix~\ref{appendix:flowsde}):"
- Fokker–Planck equation: A PDE describing the time evolution of probability densities under stochastic processes. "This preserves what we term forward consistencyâthe adherence of the diffusion model's underlying probability density to the Fokker-Planck equation \citep{oksendal2003stochastic,song2020score}"
- Forward consistency: Ensuring the learned model’s density evolution matches the forward diffusion process (not just reverse-time sampling). "This preserves what we term forward consistencyâthe adherence of the diffusion model's underlying probability density to the Fokker-Planck equation"
- GRPO: Group Relative Policy Optimization; a policy-gradient-style RL algorithm variant used for post-training. "This makes transitions between adjacent steps tractable Gaussians, enabling direct application of existing RL algorithms like GRPO to the diffusion domain~\citep{xue2025dancegrpo, liu2025flow}."
- Guidance strength: A scalar that scales the added guidance direction applied to the base policy’s velocity. "We term reinforcement guidance, and guidance strength."
- Guidance-free training: Training the model to internalize guidance so no external guidance is needed at inference. "This technique, inspired by recent advances in guidance-free training \citep{gft}, allows us to perform RL continuously on a single policy model, which is crucial to online reinforcement."
- Implicit parameterization: A technique where target positive/negative policies are defined as linear functions of the old and current models, avoiding training separate models. "it adopts an implicit parameterization technique that allows integrating reinforcement guidance directly into the optimized policy."
- Importance sampling: A weighting method for off-policy corrections; here explicitly avoided. "Finally, it is a native off-policy algorithm, naturally allowing decoupled training and sampling policies without importance sampling."
- Jensen's inequality: A convexity inequality used here to derive tractable bounds for likelihood-related objectives. "Whether approximating the marginal data likelihood with variational bounds and applying Jensen's inequality to reduce loss computation cost~\citep{wallace2024diffusion}"
- Likelihood-free: An approach that does not rely on explicit or approximate likelihood computation. "In contrast, DiffusionNFT is inherently likelihood-free, bypassing such compromises."
- LoRA: Low-Rank Adaptation; a parameter-efficient finetuning method adding low-rank adapters to large models. "We finetune with LoRA (, )."
- Marginal data likelihood: The probability of observed data under a model, marginalized over latent variables; hard to compute in diffusion. "Whether approximating the marginal data likelihood with variational bounds and applying Jensen's inequality to reduce loss computation cost"
- Markov Decision Process (MDP): A formalism defining states, actions, transitions, and rewards for sequential decision-making. "recent works~\citep{black2023training,fan2023dpok, liu2025flow,xue2025dancegrpo} formulate the diffusion sampling as a multi-step Markov Decision Process (MDP)."
- Off-policy: RL training where the behavior (data-collecting) policy differs from the optimized policy. "Finally, it is a native off-policy algorithm, naturally allowing decoupled training and sampling policies without importance sampling."
- On-policy: RL training where data is collected from the current policy being optimized. "Fully on-policy () accelerates early progress but destabilizes training"
- Ordinary Differential Equation (ODE): A deterministic time-evolution equation used to model reverse diffusion flows. "Reverse sampling typically follows the ODE form~\citep{song2020score} of the diffusion model"
- Policy Gradient: A family of RL methods that optimize policies by ascending gradients of expected returns. "Policy Gradient algorithms assume that model likelihoods are exactly computable."
- Proximal Policy Optimization (PPO): A popular policy-gradient RL algorithm using clipped objectives for stability. "In order to apply Policy Gradient algorithms such as PPO \citep{schulman2017proximal} or GRPO \citep{shao2024deepseekmath} to diffusion models"
- Rectified flow: A specific flow schedule with linear paths simplifying the velocity target. "Rectified flow~\citep{liu2022flow} can be considered as a simplified special case of the above-discussed diffusion models, where "
- Rejection FineTuning (RFT): Training only on high-reward (positive) samples by rejecting low-reward ones. "previous work \citep{lee2023aligning} performs diffusion training solely on , known as Rejection FineTuning (RFT)."
- Reparameterization: Expressing a random variable as a deterministic function of parameters and noise for tractable gradients or sampling. "enabling reparameterization as \begin{equation*} _t=\alpha_t_0+\sigma_t,\sim(\bm 0,). \end{equation*}"
- Reward-Weighted Regression (RWR): An offline RL method that fits a policy to data weighted by rewards. "Reward-Weighted Regression (RWR)~\citep{lee2023aligning} is an offline finetuning method but lacks a negative policy objective to penalize low-reward generations."
- Score-based RL: Approaches that optimize directly over the score (gradient of log-density) rather than likelihoods. "Score-based RL. These methods try to perform RL directly on the score rather than the likelihood field \citep{zhu2025dspo}."
- Soft Update: Gradual parameter update of a target/behavior policy toward the online policy for stability. "Soft Update of Sampling Policy."
- Stochastic Differential Equation (SDE): A stochastic time-evolution equation modeling noisy diffusion dynamics. "FlowGRPO~\citep{liu2025flow} addresses this by using the SDE form~\citep{song2020score}"
- Stop-gradient operator: An operation that prevents gradients from flowing through a term during backpropagation. "where sg is the stop-gradient operator."
- Transition kernel: The conditional distribution specifying how states evolve over diffusion time. "The forward noising process admits a closed-form transition kernel $\pi_{t|0}(_t|_0)=(\alpha_t_0,\sigma_t^2)$"
- Variational bounds: Lower bounds (e.g., ELBO) used to approximate intractable likelihoods. "Whether approximating the marginal data likelihood with variational bounds and applying Jensen's inequality to reduce loss computation cost"
- Velocity parameterization: Modeling diffusion dynamics by predicting velocity (the tangent of the transport trajectory) instead of noise or data directly. "One way to learn diffusion models is to adopt the velocity parameterization ~\citep{zheng2023improved}, which predicts the tangent of the trajectory"
Collections
Sign up for free to add this paper to one or more collections.