Dualities in Physics (2509.15866v1)
Abstract: For more than half a century, dualities have been at the heart of modern physics. From quantum mechanics to statistical mechanics, condensed matter physics, quantum field theory and quantum gravity, dualities have proven useful in solving problems that are otherwise quite intractable. Being surprising and unexpected, dualities have been taken to raise philosophical questions about the nature and formulation of scientific theories, scientific realism, emergence, symmetries, explanation, understanding, and theory construction. This book discusses what dualities are, gives a selection of examples, explores the themes and roles that make dualities interesting, and highlights their most salient types. It aims to be an entry point into discussions of dualities in both physics and philosophy. The philosophical discussion emphasises three main topics: whether duals are theoretically equivalent, the view of scientific theories that is suggested by dualities (namely, a geometric view of theories), and the compatibility between duality and emergence.
Summary
- The paper introduces a formal schema defining dualities as structure-preserving isomorphisms between models, establishing a common core theory.
- It demonstrates the practical utility of dualities through examples like Fourier, Kramers-Wannier, and T-duality to handle complex regimes.
- The work explores philosophical implications by analyzing theoretical equivalence, emergence, and a geometric view of scientific theories.
Dualities in Physics: Structure, Examples, and Philosophical Implications
Introduction: The Centrality of Dualities
Dualities have become a foundational concept in contemporary physics, permeating quantum mechanics, statistical mechanics, condensed matter, quantum field theory (QFT), and quantum gravity. The paper "Dualities in Physics" (2509.15866) provides a systematic framework for understanding dualities as isomorphisms between physical theories, emphasizing both their technical utility and their philosophical significance. The authors introduce a Schema for dualities, formalizing them as structure-preserving bijections between models, and explore the implications for theory construction, interpretation, and equivalence.
Formal Schema for Dualities
The Schema treats a physical theory as a triple of state-space, quantities, and dynamics. A duality is defined as a pair of isomorphisms and between the state-spaces and sets of quantities of two models, equivariant with respect to the dynamics. This formalism enables precise characterization of dualities, distinguishing them from symmetries (which are automorphisms of state-spaces or quantities) and from quasi-dualities (which are approximate or regime-limited correspondences).
Interpretation is addressed via internal and external mappings: internal interpretations focus on duality-invariant structure (the common core theory), while external interpretations include model-specific features. The common core theory is the mathematical structure invariant under the duality map, analogous to the abstract group underlying its representations.
Exemplary Dualities Across Physics
Position-Momentum Duality in Quantum Mechanics
Fourier duality exemplifies the Schema: the Fourier transform provides a unitary isomorphism between position and momentum representations in Hilbert space, preserving inner products and operator algebra. The common core is Hilbert space quantum mechanics, with the duality manifest as a change of basis. This case illustrates the "hard-easy" theme: certain problems are tractable in one representation but intractable in the other.
Kramers-Wannier Duality in Statistical Mechanics
Kramers-Wannier duality relates the partition functions of the 2D Ising model at high and low temperatures via a nontrivial mapping of the inverse temperature parameter. The duality enables determination of the critical temperature and order-disorder transitions, with the magnetization and its dual serving as order and disorder parameters. This duality is paradigmatic for phase transitions and symmetry breaking, and highlights the heuristic power of dualities in connecting distinct physical regimes.
Electric-Magnetic Duality in Maxwell Theory
Electric-magnetic duality exchanges electric and magnetic fields in Maxwell's equations, both in component and Lorentz-covariant (Hodge dual) formulations. The Dirac quantization condition is invariant under the duality, and the duality maps weakly coupled electric regimes to strongly coupled magnetic ones, exemplifying the "hard-easy" and "elementary-composite" themes. The common core is a complex vector field theory, with duality corresponding to a rotation in the complex plane.
Dualities in Quantum Field Theory and Gravity
Electric-magnetic duality in QFT, especially in supersymmetric Yang-Mills theories, relates elementary particle states to solitonic monopole states. In SYM, Montonen-Olive duality conjectures a self-duality, with electric and magnetic states matched in mass and spin. In SYM, Seiberg-Witten theory exhibits quasi-duality between low-energy effective models in different regions of moduli space, motivating the geometric view of theories as differentiable manifolds with duality maps as transition functions.
T-Duality and the Web of String Theories
T-duality in string theory equates models with compact dimensions of radius and $1/R$, exchanging momentum and winding modes. This duality is central to the web of perturbative string theories and points toward the existence of M-theory as a non-perturbative unification (Figure 1).
Figure 1: Relations between the five superstring theories and 11-dimensional supergravity, with M-Theory at the center as the unifying framework.
T-duality's invariance of the mass spectrum under and demonstrates the deep equivalence of apparently distinct geometrical backgrounds, challenging naive ontological interpretations of spacetime.
AdS/CFT and Bulk Reconstruction
AdS/CFT duality posits an isomorphism between quantum gravity in -dimensional AdS spacetime and a -dimensional conformal field theory on its boundary. The duality is formalized via the equivalence of partition functions and path integrals, with the 't Hooft coupling controlling the regime of validity. Bulk reconstruction, via entanglement wedge reconstruction and quantum error-correcting codes, provides a concrete mechanism for encoding semiclassical bulk quantities in boundary CFT operators, with implications for black hole entropy and the information paradox.
Philosophical Analysis: Theory Equivalence, Geometric View, and Emergence
Theoretical Equivalence
Dualities raise nuanced questions about theoretical equivalence. The paper argues for a mixed criterion: formal equivalence (duality as isomorphism) is necessary but not sufficient; interpretative equivalence (shared domain of application) is also required. Internal interpretations support theoretical equivalence, while external interpretations may not. The analysis distinguishes cases where duals are clearly equivalent (e.g., position-momentum duality), clearly inequivalent (e.g., high vs. low temperature Ising models), and intermediate cases requiring further scrutiny.
Geometric View of Theories
Quasi-dualities and moduli space structures motivate a geometric view of theories, replacing the "flat" semantic conception (theory as a set of models) with a differentiable manifold equipped with transition functions (dualities) between local coordinatizations. This perspective is essential for understanding phase structure, order parameters, and the global organization of physical theories.
Emergence and Duality
The paper clarifies that duality, as a symmetric relation, is incompatible with emergence, which is asymmetric. However, emergence can occur beside duality, as in bulk reconstruction, where semiclassical gravity emerges from fundamental quantum gravity degrees of freedom encoded in the boundary CFT. Effective dualities, valid only in certain regimes, can also instantiate emergence, as in emergent gravity scenarios.
Implications and Future Directions
The systematic treatment of dualities has profound implications for both physics and philosophy. Practically, dualities enable tractable calculations in strongly coupled regimes, guide theory construction, and unify disparate physical phenomena. Philosophically, they challenge traditional notions of theory individuation, ontology, and fundamentality, motivating structural realist positions and geometric conceptions of scientific theories.
Future work should further develop the common core theory for diverse dualities, explore the relationship between dualities and symmetries, and refine the geometric view in connection with theoretical equivalence and emergence. The interplay between dualities and quantum gravity, especially in holographic and string-theoretic contexts, remains a fertile ground for both technical and conceptual advances.
Conclusion
"Dualities in Physics" provides a rigorous framework for understanding dualities as isomorphisms between physical theories, illustrated by canonical and advanced examples across physics. The Schema enables precise analysis of dualities' structure, interpretation, and philosophical consequences, highlighting their role in theory construction, heuristic reasoning, and the unification of physical laws. The geometric view and the nuanced treatment of theoretical equivalence and emergence open new avenues for foundational research, both in physics and in the philosophy of science.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What Is This Paper About?
This paper is about “dualities” in physics. A duality is when two very different-looking theories turn out to describe the same physical reality in perfectly matching ways. Think of it like two languages telling the same story: the words and grammar differ, but the plot, characters, and events line up one-to-one.
The authors explain what dualities are, show famous examples from many parts of physics, and explore what dualities mean for big ideas in philosophy of science, like when two theories count as “the same,” how theories should be built, and how new things (like spacetime) can “emerge” from something else.
What Questions Are They Asking?
In simple terms, the paper asks:
- What exactly is a duality, and how do we recognize one?
- When do two dual theories count as truly “the same theory,” and when are they just different but equally good descriptions?
- How can dualities help us do hard calculations by turning them into easier ones?
- What do dualities tell us about how to build and interpret scientific theories?
- Can duality fit with the idea that big things (like spacetime or phases of matter) can emerge from smaller building blocks?
How Do They Study It? (Approach and Analogies)
The authors use a clear framework (they call it a “Schema”) to make dualities precise. Here’s the everyday version of their approach:
- The “triple” idea: They say every theory has three basic parts, like a video game:
- States: all the possible situations you can be in (like all the levels or character positions).
- Quantities: what you can measure (like your score, health, or time).
- Dynamics: how things change (the game’s rules, like how you move or level up).
- A duality is a perfect matching (a one-to-one, rule-respecting “translation”) between two theories’ states, quantities, and dynamics. In math, that kind of perfect matching is called an “isomorphism,” but you can think “exact translator.”
- Common core theory: Behind two dual theories, there’s a shared “story engine” that both versions run on. The authors call this the “common core.” Each dual theory is like a different user interface for the same engine.
- Interpreting the theories:
- Internal interpretation: focus only on what both theories share (the common core). Then the two are “the same” in what they say about the world.
- External interpretation: also include each theory’s extra features that the other doesn’t have. Then the two can describe the world in slightly different ways.
- Themes they track:
- Hard–easy: a tough problem in one theory becomes an easy problem in its dual. It’s like switching from a maze view to a map view.
- Elementary–composite: “basic” objects in one theory show up as “built-from-parts” in the other, and vice versa.
- Exact–effective: some dualities are exact matches; others are “good enough” in certain conditions (like using a simplified recipe that still tastes right).
They illustrate all this with examples across physics: quantum mechanics (position–momentum), electromagnetism (electric–magnetic), statistical mechanics (the Ising model and phase changes), condensed matter (vortices and the BKT transition), quantum field theory (Yang–Mills), and quantum gravity (AdS/CFT, which links gravity to a theory without gravity on a boundary).
What Did They Find, and Why Does It Matter?
Here are the main takeaways and their importance:
- Dualities are powerful “translators” across physics.
- Importance: They connect areas that seem unrelated—like materials in the lab and theories of gravity—showing deep unity in nature, not just superficial similarities.
- Dualities often turn hard problems into easy ones.
- Example: Strong interactions in one theory (where usual tricks fail) become weak and manageable in the dual. It’s like turning down the “difficulty knob” by switching viewpoints.
- Importance: This opens doors to solving problems we couldn’t handle before, from how materials change phase to how particles get “confined.”
- Whether two dual theories are truly “the same” depends on how we interpret them.
- If we focus only on the shared core, the theories are equivalent.
- If we also care about each theory’s extra features, they can come apart.
- Importance: This gives a careful, honest answer to the question “Are duals the same theory?”—it’s not always yes or no; it depends on what counts as physically meaningful.
- Dualities suggest a “geometric view” of theories.
- Instead of thinking of a theory as just a bag of models, the authors argue a theory is more like a shaped space with structure (a smooth “landscape”), and the duals are different but equivalent coordinate maps on that landscape.
- Importance: This helps organize theories more clearly and shows why dualities are possible.
- Duality and emergence can fit together.
- In some cases, what looks like space or gravity might “emerge” from a dual description without gravity (as in AdS/CFT).
- Importance: That’s a big clue about how our familiar world could come from something more basic.
- Dualities match not just equations but mechanisms.
- They don’t only relate formulas; they also align the physical “stories” on both sides—like how defects in materials can match particle-like objects in a dual theory.
- Importance: This gives scientists new ways to model, simulate, and understand real systems.
Why This Work Could Matter Going Forward
- Better tools for tough problems: Dualities can turn impossible calculations into doable ones, helping with things like phase transitions, confinement in particle physics, and even black hole puzzles.
- Bridges between fields: They connect lab physics (like superconductors) with high-energy theory (like quantum gravity), allowing ideas to flow both ways.
- Smarter theory-building: The “geometric view” and the focus on the common core can guide how we design future theories.
- Clearer philosophy of science: The paper gives a precise way to talk about when theories are “the same,” how explanations work across dual descriptions, and how new properties might emerge.
In short, by showing how different-looking theories can be secretly the same, this work gives scientists and philosophers a common toolkit: a way to translate, compare, and learn from many corners of physics—making the hard parts easier, the strange parts clearer, and the connections deeper.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of concrete gaps and unresolved questions that arise from the paper’s framing, scope, and methodological choices—each item is formulated to guide actionable research.
- Provide a unified, mathematically precise definition of duality that applies across domains (QM, SM, CM, QFT, QG), potentially via category theory or logic, and addresses criticisms that simple “isomorphism” is too strict or ill-suited in some cases.
- Develop general, constructive procedures to identify and build the “common core theory” for a given dual pair: criteria for existence, uniqueness, minimality/augmentedness, and algorithms for extracting the change of variables and dynamical structure.
- Formalize a mixed criterion for theoretical equivalence that integrates formal duality with interpretation; supply decision procedures and case studies showing when duals are (or are not) theoretically equivalent, and how this relates to empirical equivalence.
- Clarify the internal vs external interpretation choice: methodological guidelines for selecting one over the other, implications for ontology and empirical content, and worked examples where the interpretive choice changes conclusions.
- Establish how observations in one domain (e.g., condensed matter experiments) can confirm, constrain, or undercut claims on a dual theory in a distant domain (e.g., gravity via AdS/CFT); design discriminating empirical tests and validation protocols.
- Systematize “off-shell” dualities: conditions under which on-shell state/observable maps extend to action/path-integral equivalence (including measure factors, boundary terms, and anomalies) in classical and quantum settings.
- Handle gauge constraints rigorously within the Schema: articulate how value-preservation and equivariance are ensured for gauge-invariant quantities, and what role BRST quantization or reduced phase spaces play in duality maps.
- Characterize quantum dualities with inequivalent classical precursors: necessary and sufficient conditions under which inequivalent classical theories quantize to the same quantum theory, and a taxonomy of distinct classical limits of a single quantum core.
- Clarify bulk reconstruction and emergence in AdS/CFT: state general conditions, error bounds, and limitations (subregion duality, state-dependence, gravitational dressing); address time dependence, horizons, and non-perturbative bulk locality.
- Develop a methodology for “matching of physical mechanisms” across duals (e.g., confinement, symmetry breaking): criteria for legitimate mechanism-transfer, limitations, and templates for reconstructing mechanisms in the dual model.
- Elaborate and evaluate the “geometric view of theories”: its formal articulation beyond examples, relation to (and advantages over) the semantic view, and tests in domains where geometric structure is less evident.
- Precisely define quasi-dualities/effective dualities: metrics for approximation quality, domain-of-validity diagnostics, and conditions under which quasi-dual inferences are reliable for explanation or prediction.
- Extend elementary case studies beyond idealizations:
- Electric–magnetic duality: include sources, θ-terms, monopoles, boundary conditions, nontrivial topology, and non-Abelian S-duality; address quantum anomalies and strong-coupling regimes.
- Kramers–Wannier duality: analyze order/disorder variable interpretation, finite-size and boundary effects, higher-dimensional generalizations, gauge–Ising dualities, and implications for universality and emergence.
- Particle–soliton (vortex) dualities: rigorous derivations in realistic materials, precise mapping of topological vs Noether currents, and experimental protocols testing BKT-like dual predictions.
- Distinguish dualities from symmetries and mere analogies: principled, formal criteria and diagnostics for inter-theoretic duality vs intra-theoretic automorphism or heuristic analogy.
- Quantify the “hard–easy” theme in complexity terms: classify problems by computational complexity under duality, and identify when duality yields polynomial/exponential speedups or improved numerical stability.
- Explore dualities beyond equilibrium and AdS: non-equilibrium dynamics, finite density/temperature, time-dependent backgrounds, de Sitter or non-AdS holography, and non-unitary theories.
- Relate dualities to logical equivalence frameworks: explicit mappings to definitional/Morita equivalence and categorical equivalence of model categories; limits of logical tools for capturing physical dualities.
- Systematize heuristic roles of dualities in theory construction: articulate success conditions, failure modes, and discovery heuristics; assess bottom-up holographic modeling’s epistemic status and error control.
- Clarify ontological commitments under duality: identify duality-invariant quantities/structures that warrant realist commitment and articulate how internal/external interpretations affect underdetermination.
- Specify practical selection criteria between dual formulations: guidance on when to prefer a dual for explanation, computation, or pedagogy, including trade-offs with approximation error and interpretive clarity.
- Analyze the role of global/topological data in dualities: boundary terms, edge modes, higher-form symmetries, and anomaly matching as necessary consistency checks for dual equivalence.
- Compile a standardized, cross-domain map of established dualities with shared notation and metadata (assumptions, regimes, equivalence type) to enable systematic comparison and identification of missing links.
Practical Applications
Practical Applications Derived from “Dualities in Physics”
Below are actionable applications that follow from the paper’s findings, methods, and conceptual innovations (e.g., the Duality Schema, common core theory, internal/external interpretations, and exemplar dualities such as Kramers–Wannier, particle–soliton/BKT, electric–magnetic duality, position–momentum duality, and AdS–CFT). Each item notes sector links, tools/workflows, and assumptions/dependencies that affect feasibility.
Immediate Applications
The following applications can be deployed now with existing theory, software, and practices, acknowledging domain-specific validation and scope.
- Duality-aware modeling and review in research groups (Academia, Software)
- Use case: Adopt the Schema for dualities and “common core theory” explicitly in paper-writing, code repositories, and seminars to clarify when two models are formally equivalent versus merely analogous.
- Tools/workflows: Duality checklists in lab SOPs; shared “common-core” notebooks that capture the invariant triple S–Q–D; duality maps documented as code (e.g., change-of-variable modules).
- Assumptions/dependencies: Team literacy in isomorphisms and model interpretation; availability of dual formulations for the target phenomena.
- Cross-validation of simulations via dual runs (Academia, Software/HPC)
- Use case: Verify computational results by simulating both sides of a known duality (e.g., 2D Ising under Kramers–Wannier; Fourier-domain vs spatial-domain solvers for position–momentum duality; EM duality in vacuum) and checking value-preservation and equivariance.
- Tools/workflows: “Dual-run” harnesses that compare observables across dual frames; invariant test suites; CI/CD integration for physics codes.
- Assumptions/dependencies: Known dual transforms are correct for the regime; numerical errors are controlled and comparable across frames.
- Thin-film superconductors and 2D materials analysis with BKT physics (Materials, Energy, Academia)
- Use case: Diagnose and tune vortex dynamics, critical temperatures, and phase transitions in 2D superconductors/superfluids using particle–soliton dualities and the BKT framework.
- Tools/workflows: Data pipelines that fit vortex-antivortex models; experimental workflows that probe topological vs Noether currents; dual-domain parameter inference.
- Assumptions/dependencies: Sample quality and controlled disorder; the system is in the regime where BKT applies (e.g., quasi-2D, appropriate temperature ranges).
- Holography-inspired transport calculations for strongly correlated systems (Materials, Software/HPC, Academia)
- Use case: Use AdS–CFT-inspired recipes to estimate transport coefficients (e.g., DC conductivity, viscosity) when conventional perturbation theory fails.
- Tools/workflows: Open-source holographic solvers; surrogate modeling of gravity-side solutions to infer boundary-side observables; calibration against experimental data.
- Assumptions/dependencies: The effective holographic model captures dominant physics in the material; quasi-duality suffices for predictive use; careful uncertainty quantification.
- Electromagnetics design leveraging electric–magnetic duality insights (Engineering, Metamaterials)
- Use case: Inform antenna/metamaterial designs that balance electric and magnetic responses; use duality-invariant reasoning to avoid overfitting to one modality.
- Tools/workflows: Dual-field parameter sweeps; EM solvers that monitor duality-invariant quantities; design patterns that identify symmetry breaking (e.g., presence of charges/currents).
- Assumptions/dependencies: Materials with tunable permeability; duality symmetry holds approximately in targeted configurations.
- Signal processing and imaging pedagogy grounded in position–momentum duality (Education, Software)
- Use case: Improve teaching and practice of Fourier-domain methods (filter design, denoising, compression) by framing them as dual descriptions of the same physical model.
- Tools/workflows: Dual-domain labs (time/space vs frequency); assessment of value-preservation across transforms; curriculum modules linking QM duality to DSP.
- Assumptions/dependencies: Alignment between abstract duality and practical transforms; learner familiarity with basic linear algebra.
- Model scope management via internal vs external interpretations (Software/Industry, Digital Twins)
- Use case: Prevent scope creep and misinterpretation in digital twins by distinguishing duality-invariant core features (internal interpretation) from frame-specific details (external interpretation).
- Tools/workflows: Model governance templates; metadata schemas that tag “common core” vs “specific structure”; decision logs for interpretation choices.
- Assumptions/dependencies: Organizational adoption of interpretation standards; traceable mapping from models to domains of application.
- Research governance and funding evaluation (Policy, Academia)
- Use case: Encourage interdisciplinary proposals that explicitly use dual methods to tackle non-perturbative problems; require duality or quasi-duality cross-checks in complex modeling.
- Tools/workflows: Proposal rubrics that score duality use; post-award milestones that demonstrate dual-domain validation; reproducibility audits.
- Assumptions/dependencies: Willingness to prioritize method rigor; reviewers trained in duality concepts; clear boundaries between exact dualities and quasi-dualities.
Long-Term Applications
These applications may require further research, experimental validation, scaling, tooling, or community consensus before broad deployment.
- Predictive materials design via gravity-based solvers (Materials, Energy, Software/HPC)
- Use case: Industrial workflows that use AdS–CFT-derived surrogates to design strongly correlated materials (high-temperature superconductors, strange metals).
- Tools/products: “Holographic materials studio” platforms; integrated lab–simulation loops; UQ pipelines specific to quasi-duality regimes.
- Assumptions/dependencies: Demonstrated predictive accuracy across materials classes; stable numerical methods for bulk reconstruction; robust mapping from lab observables to dual variables.
- Automated “common core” extraction and duality mapping (Software/IT, Academia)
- Use case: Software that takes multiple model formulations and automatically discovers common-core S–Q–D structure and candidate duality maps (possibly using category-theoretic tooling).
- Tools/products: Duality-aware model compilers; symbolic-algebra engines with isomorphism detection; IDE plugins for duality checks.
- Assumptions/dependencies: Formalization of models in machine-readable languages; scalable algorithms for equivalence discovery; community standards for representations.
- Duality-informed AI/ML architectures (Software/AI, Academia)
- Use case: Equivariance-aware neural networks that enforce invariances under dual transformations (e.g., frequency–space duals, EM dual rotations) to improve generalization and data efficiency.
- Tools/products: Physics-informed ML libraries with dual constraints; benchmark suites comparing dual-equivariant vs standard models.
- Assumptions/dependencies: Mapped duals are exact or sufficiently tight; reliable training datasets including paired dual-domain examples; performance gains justify complexity.
- Quantum technologies leveraging topological dualities (Quantum Computing, Materials)
- Use case: Error-correcting codes and qubit architectures exploiting particle–soliton dualities and topological order for robustness against local noise.
- Tools/products: Topological qubit platforms; duality-guided code design workflows; simulation stacks for vortex-based protection.
- Assumptions/dependencies: Viable materials with long coherence times; scalable fabrication; proven fault-tolerance thresholds.
- Energy infrastructure with next-gen superconductors (Energy, Materials)
- Use case: Grid components utilizing materials engineered with insights from BKT transitions and dualities to minimize losses in realistic operating conditions.
- Tools/products: Duality-informed materials screening; pilot deployments; monitoring systems that track topological-defect dynamics.
- Assumptions/dependencies: Stable supply chains and manufacturability; environmental tolerance; regulation and safety certification.
- Metamaterials with tunable EM dual behavior (Engineering, Defense, Sensing)
- Use case: Devices that approximate EM dual symmetry for advanced stealth, sensing, or communications, and that can be reconfigured across operating regimes.
- Tools/products: Metamaterial libraries with duality metrics; adaptive control systems adjusting electric/magnetic responses; integrated design simulators.
- Assumptions/dependencies: Practical materials achieving target permeability/permittivity; reliability across temperature/frequency ranges; cost-effective manufacturing.
- Standards for duality metadata in scientific publishing and software (Policy, Academia, Software)
- Use case: Community standards that require duality statements (exact/quasi, maps, common core) to enhance reproducibility and model governance.
- Tools/products: Duality metadata schemas; journal and repository compliance tooling; reviewer training packages.
- Assumptions/dependencies: Broad community buy-in; interoperability across publishers and code platforms; incentives for compliance.
- Immersive education and virtual labs across dual frames (Education)
- Use case: Learning environments where students solve problems in both duals (e.g., Ising vs dual spins; boundary vs bulk) to internalize hard–easy and elementary–composite themes.
- Tools/products: Interactive simulators; scaffolded exercises enforcing value-preservation; cross-domain assessments.
- Assumptions/dependencies: Institutional support; platform integration; validated pedagogy.
- Cross-domain analog simulation frameworks via dualities (Academia, R&D)
- Use case: Systematic use of lab-realizable systems (condensed matter) to paper inaccessible regimes (high-energy/gravity) via dual mappings, beyond informal analogies.
- Tools/products: Registry of admissible dual analogs; experimental–theoretical workflow templates; shared datasets for mechanism matching.
- Assumptions/dependencies: Verified isomorphisms or strong quasi-duality; instrumentation capable of resolving the relevant observables; agreed protocols for mechanism reconstruction.
- Duality-informed solutions to inverse problems and bulk reconstruction (Software/HPC, Imaging)
- Use case: Translate bulk–boundary reconstruction ideas into general inverse-problem solvers (e.g., tomography, complex network inference) that exploit dual-domain constraints.
- Tools/products: Reconstruction libraries enforcing dual constraints; performance benchmarks on imaging and PDE inverse problems.
- Assumptions/dependencies: Mathematical translation from AdS–CFT techniques to target inverse problems; demonstrable advantage over classical regularization methods.
Notes common to several applications:
- Many benefits hinge on the hard–easy theme (strong–weak coupling inversion), enabling non-perturbative insights via dual frames.
- The distinction between internal vs external interpretations is crucial for model governance: misinterpretation of frame-specific structure can invalidate conclusions.
- Where dualities are quasi-dualities, rigorous uncertainty quantification and domain-of-validity documentation are essential before high-stakes deployment.
Glossary
- AdS: Anti-de Sitter space; a spacetime of constant negative curvature used in holography and quantum gravity. "in AdS"
- AdS-CFT: A duality relating a gravity theory in AdS to a conformal field theory on its boundary. "under the umbrella of AdS-CFT"
- algebraic-geometric structures: Structures from algebraic geometry used to endow model spaces with geometric features beyond set-theoretic structure. "algebraic-geometric structures"
- automorphism: A structure-preserving map from a mathematical object to itself. "an automorphism of state-spaces and quantities"
- bare theory: The uninterpreted common-core triple of states, quantities, and dynamics that underlies dual models. "the bare theory"
- Berezinskii-Kosterlitz-Thouless phase transition: A topological phase transition in two-dimensional systems driven by vortex unbinding. "Berezinskii-Kosterlitz-Thouless phase transition"
- black hole entropy counting: Microstate-counting methods (often in string theory) accounting for black hole entropy. "black hole entropy counting"
- bulk reconstruction: Recovering bulk gravitational data/observables from boundary CFT data in holography. "bulk reconstruction in AdS-CFT"
- category theory: A mathematical framework centered on objects and morphisms, used to reformulate equivalences. "category theory or other mathematical tools"
- colour charge confinement: The QCD phenomenon that color-charged particles (quarks, gluons) cannot be isolated. "colour charge confinement"
- commutative diagram: A diagram of maps that encodes equations via path-independence of composition. "the commutative diagram"
- common core theory: The theory capturing duality-invariant structure of dual models, from which they can be represented. "common core theory"
- conformal quantum field theory: A quantum field theory invariant under conformal (angle-preserving) transformations. "a conformal quantum field theory"
- correlation functions: Expectation values of products of fields/operators that encode dynamics and observables in QFT. "complete sets of correlation functions"
- coupling constant: A parameter controlling the strength of interactions in a theory. "coupling constants characterise the strength of interactions"
- D-branes: Extended objects in string theory on which open strings end and which carry gauge dynamics. "D-branes"
- differentiable manifold: A smooth space allowing calculus, often used to model the structure of a theory’s state/configuration space. "a theory is best formulated as a differentiable manifold"
- electric-magnetic duality: A symmetry/duality exchanging electric and magnetic fields or charges (and couplings). "electric-magnetic duality of the Maxwell theory in vacuum"
- empirical equivalence: When two theories agree on all observable predictions for relevant phenomena. "empirical equivalence"
- equivariance: The property of a map commuting with dynamics or symmetry actions. "Equivariance of duality and dynamics, for states and quantities."
- ferromagnetic: A magnetically ordered phase with spontaneous magnetization. "ferromagnetic"
- geometric view of theories: The stance that theories are best represented by geometrically structured spaces (e.g., manifolds) rather than mere sets of models. "geometric view of theories"
- Hilbert space: A complete inner-product space serving as the state space for quantum theories. "Hilbert spaces"
- isomorphism: A bijective, structure-preserving map between mathematical structures. "a duality is an isomorphism between physical theories"
- Kramers-Wannier duality: A duality of the 2D Ising model relating low- and high-temperature regimes. "Kramers-Wannier duality"
- Lagrangian: A function whose action principle yields the equations of motion of a system. "the Lagrangians or actions"
- Lorentz-invariant: Invariant under Lorentz transformations of special relativity. "Lorentz-invariant theory"
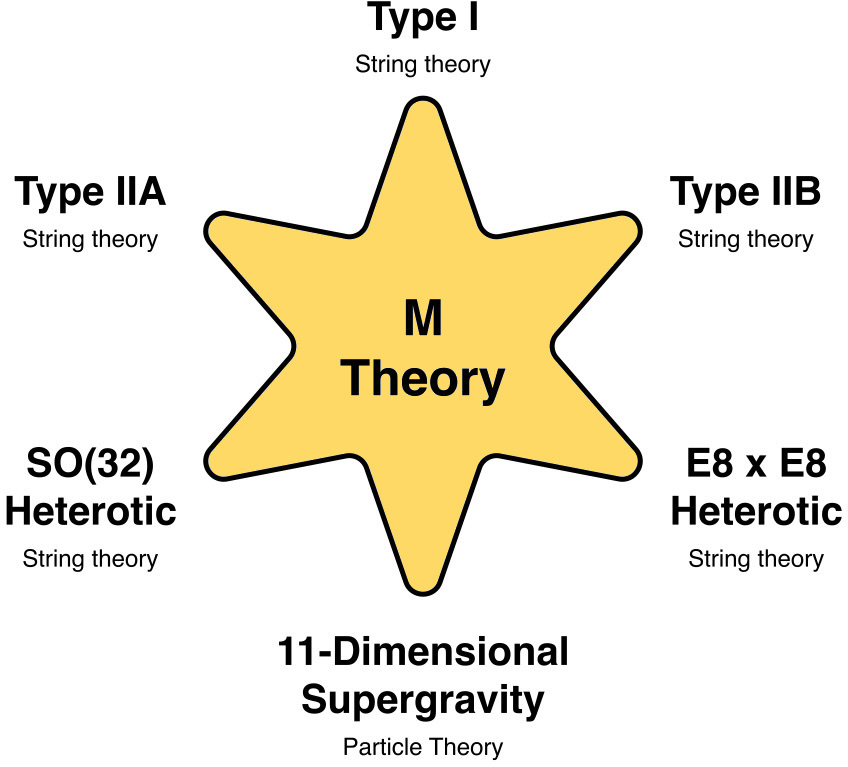
- M-theory: A proposed unifying theory underlying the various string theories. "M-theory"
- Maxwell theory: Classical electrodynamics governed by Maxwell’s equations. "Maxwell theory in vacuum"
- matrix mechanics: Heisenberg’s operator/matrix formulation of quantum mechanics. "matrix mechanics"
- monopoles: Hypothetical magnetic charges or solitonic excitations in gauge theories. "monopoles"
- Noether current: A conserved current associated with a continuous symmetry via Noether’s theorem. "a Noether current"
- non-perturbative: Refers to phenomena or methods not captured by expansions in a small parameter. "non-perturbative regime"
- off-shell: Configurations that do not satisfy the equations of motion. "off-shell"
- paramagnetic: A magnetically disordered phase that aligns only in an external field. "paramagnetic"
- perturbation theory: An approximation method expanding around a solvable limit in powers of a small parameter. "Perturbation theory is a method to approximate"
- phase transition: A qualitative change in the macroscopic state of a system as parameters (e.g., temperature) vary. "phase transition"
- position-momentum duality: The Fourier-transform duality in QM exchanging position and momentum representations. "position-momentum duality"
- quasi-dualities: Relations resembling dualities but falling short of exact isomorphism (e.g., effective or approximate). "quasi-dualities"
- quantization: The procedure of constructing a quantum theory from a classical one. "the quantization of two classical theories"
- quantum chromodynamics: The gauge theory of the strong interaction between quarks and gluons. "quantum chromodynamics"
- quantum duality: A duality where inequivalent classical theories yield equivalent quantum theories. "quantum duality"
- quantum field theory: A framework combining quantum mechanics and special relativity for fields and particles. "quantum field theory"
- quantum gravity: Approaches to quantizing gravity or describing spacetime at the quantum level. "quantum gravity"
- SO(2): The group of 2D rotations; a compact Lie group. "SO(2) and U(1)"
- solitons: Stable, localized, non-linear excitations behaving like particles. "solitons"
- state-space: The set or manifold of all possible states of a system. "state-space"
- symmetry breaking: When the ground state has less symmetry than the governing laws. "symmetry breaking"
- T-duality: A string-theoretic duality relating physics at radius R to 1/R compactifications. "T-duality"
- theoretical equivalence: Roughly, when two theories “say the same thing” under appropriate interpretation. "theoretical equivalence"
- topological current: A conserved current whose conservation follows from topology rather than a symmetry. "topological current"
- topological order: A kind of order characterized by global/topological features rather than local order parameters. "topological order"
- U(1): The group of complex phase rotations; an Abelian Lie group. "SO(2) and U(1)"
- unitary transformation: A norm-preserving linear map on a Hilbert space implementing symmetry/equivalence in quantum theory. "a unitary transformation"
- wave mechanics: Schrödinger’s wave-based formulation of quantum mechanics. "wave mechanics"
- Yang-Mills theory: A non-Abelian gauge theory generalizing electromagnetism, foundational to the Standard Model. "Yang-Mills theory"
Collections
Sign up for free to add this paper to one or more collections.