The Philosophy and Physics of Duality (2508.01616v1)

Abstract: This monograph discusses dualities in physics: what dualities are, their main examples--from quantum mechanics and electrodynamics to statistical mechanics, quantum field theory and string theory--and the philosophical questions they raise. Part I first conceptualises dualities and discusses their main roles and themes, including how they are related to familiar notions like symmetry and interpretation. It also discusses the main simple examples of dualities: position-momentum, wave-particle, electric-magnetic, and Kramers-Wannier dualities. Part II discusses advanced examples and their inter-relations: particle-soliton dualities, electric-magnetic dualities in quantum field theories, dualities in string theory, and gauge-gravity duality. This Part ends with discussions of the hole argument, and how string theory counts the microstates of a black hole. Part III is an in-depth discussion of general philosophical issues on which dualities bear: theoretical equivalence (two theories 'saying the same thing, in different words'), scientific realism and the under-determination of theories by data, theory succession and the M-theory programme, explanation, and scientific understanding. It proposes a view of scientific theories that it dubs 'the geometric view of theories'. The book's treatment of the examples is at the advanced undergraduate and graduate level, starting from elementary and progressing to more advanced examples. The discussions of philosophical topics, such as referential semantics, theoretical equivalence, scientific realism and scientific understanding, are both self-contained and in-depth. Thus the book is aimed at students and researchers with an interest in the physical examples and philosophical questions about dualities, and also in how physics and philosophy can fruitfully interact with each other.

• The paper presents a formal schema that rigorizes duality as isomorphisms between models, linking state spaces, quantities, and dynamics.
• It distinguishes between bare theories and models by introducing interpretation maps to differentiate formal equivalence from physical significance.
• The analysis uses examples from quantum mechanics, statistical mechanics, and string theory to highlight the heuristic and unifying roles of dualities.

The Philosophy and Physics of Duality: A Technical Analysis

Introduction and Motivation

"The Philosophy and Physics of Duality" (2508.01616) provides a comprehensive and systematic account of dualities in physics, integrating rigorous formalism with philosophical analysis. The work addresses duality as a central structural feature in modern theoretical physics, with applications ranging from statistical mechanics and quantum field theory to string theory. The authors' primary objective is to clarify the formal, interpretative, and heuristic roles of dualities, and to situate them within broader debates in the philosophy of science, particularly concerning theoretical equivalence, scientific realism, and the structure of physical theories.

Formal Schema for Duality

The core technical contribution is the articulation of a Schema for duality, which formalizes duality as an isomorphism between two models (in the sense of mathematical representations) of a common core theory. The common core is typically a triple $$T = \langle \mathcal{S}, \mathcal{Q}, \mathcal{D} \rangle$$, where $\mathcal{S}$ is a state space, $\mathcal{Q}$ a set (often an algebra) of quantities, and $\mathcal{D}$ a dynamics (e.g., a Hamiltonian or Lagrangian evolution).

A duality is then defined by a pair of isomorphisms:

• $$d_{\mathcal{S}}: \mathcal{S}_{M_1} \to \mathcal{S}_{M_2}$$
• $$d_{\mathcal{Q}}: \mathcal{Q}_{M_1} \to \mathcal{Q}_{M_2}$$

such that for all $s_1 \in \mathcal{S}_{M_1}$ and $Q_1 \in \mathcal{Q}_{M_1}$,

$$\langle Q_1, s_1 \rangle_1 = \langle d_{\mathcal{Q}}(Q_1), d_{\mathcal{S}}(s_1) \rangle_2$$

and the isomorphisms are equivariant with respect to the dynamics.

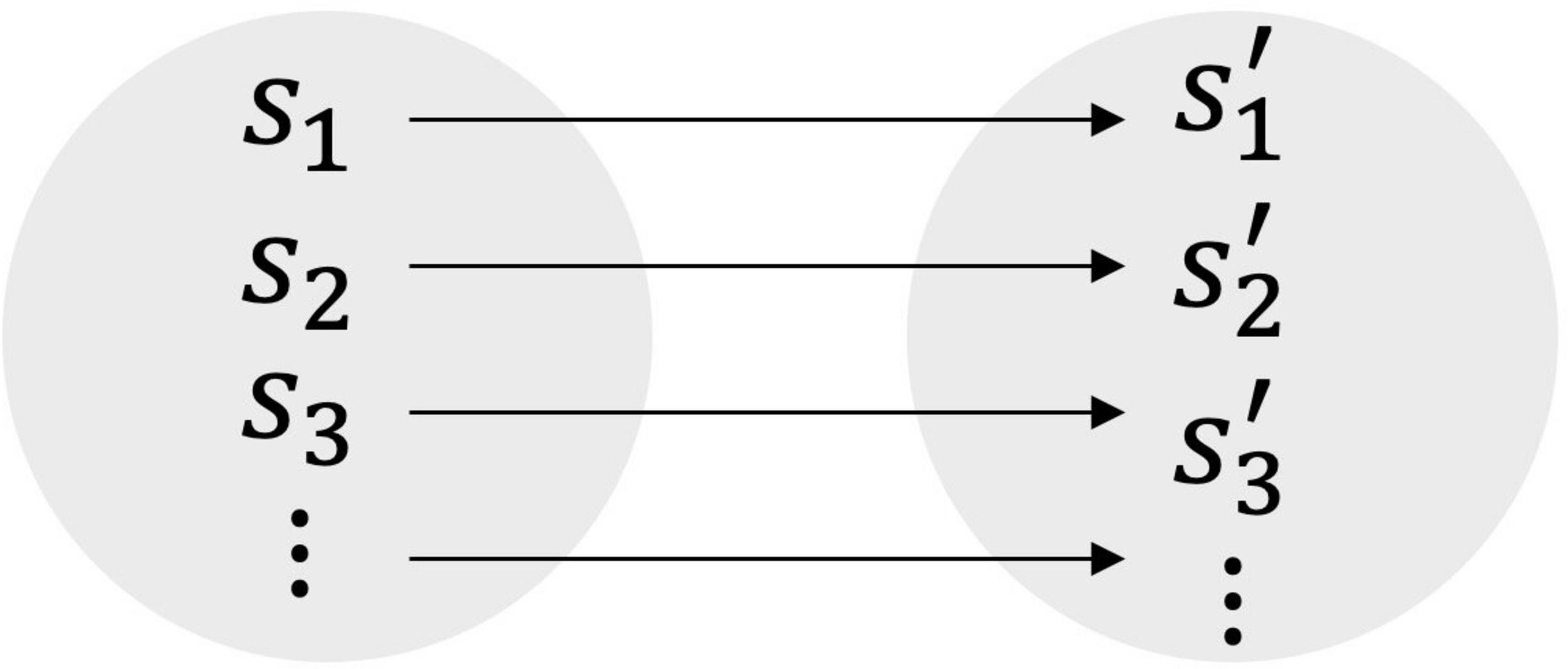
Figure 1: On the left, a theory with the set of states $s_1,s_2,s_3,\ldots$ and, on the right, a theory with the set of states $s'_1,s'_2,s'_3,\ldots$. The duality maps the states of one theory to the states of the other theory, such that the values of their respective quantities match.

This formalism is sufficiently general to encompass both classical and quantum dualities, and is robust under changes of representation (e.g., position-momentum duality in quantum mechanics, Kramers-Wannier duality in statistical mechanics, and gauge/gravity duality in string theory).

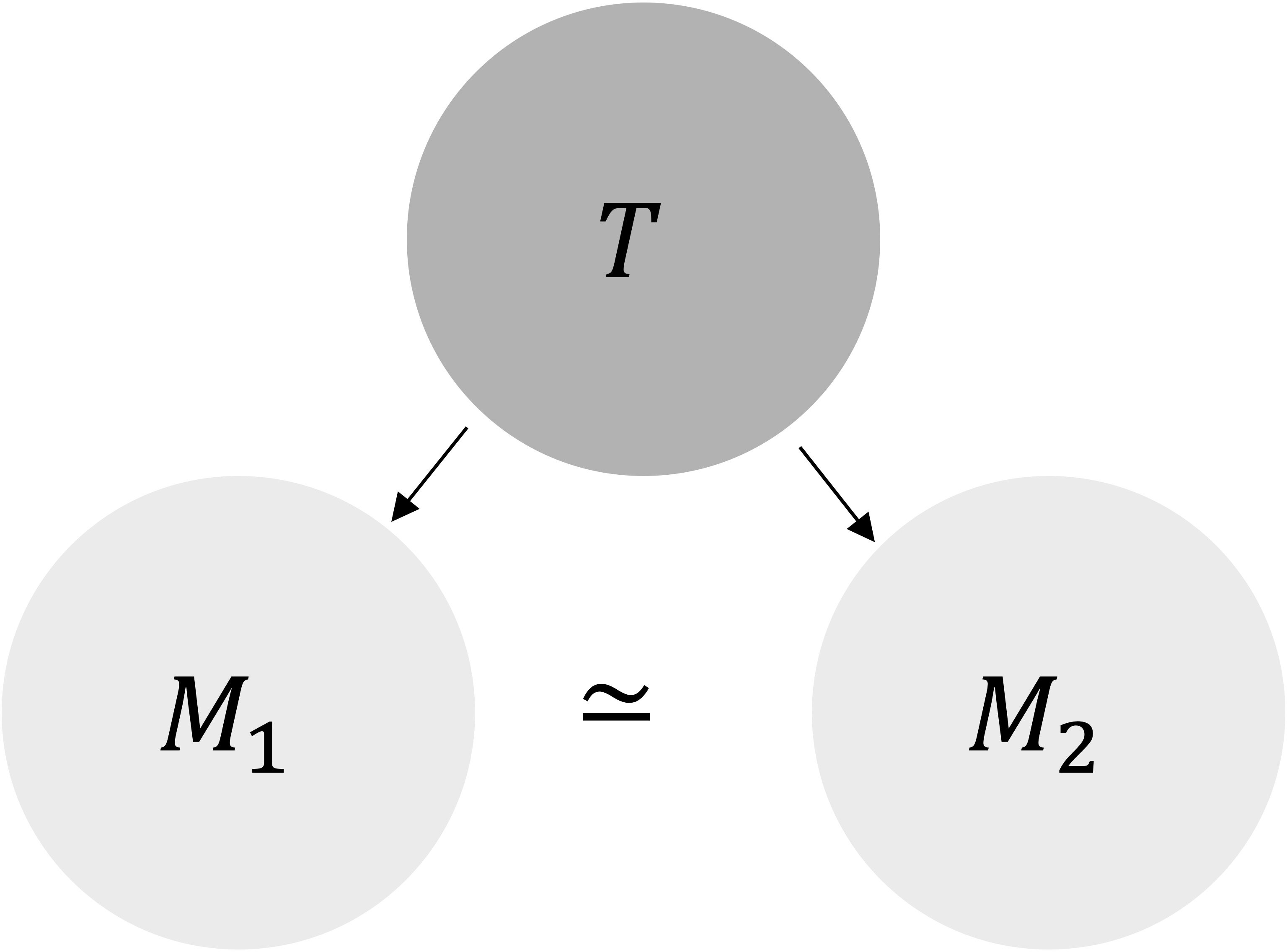
Figure 2: A common core theory, $T$, with two dual (i.e.~isomorphic) representations, $M_1$ and $M_2$.

Theories, Models, and Interpretation

A significant technical advance is the explicit distinction between bare theories (uninterpreted mathematical structures) and models (representations or realizations of the bare theory, often with additional specific structure). The authors introduce the notions of model root (the part of a model that realizes the common core) and specific structure (additional features not present in the core). This distinction is crucial for analyzing when dualities are merely formal versus when they have physical or interpretative significance.

Interpretation is formalized as a (partial) structure-preserving map from the theory or model to a domain of application. The authors distinguish internal interpretations (mapping only the model root) from external interpretations (also mapping specific structure), which is essential for analyzing theoretical equivalence and underdetermination.

Figure 3: The interpretation map $i_{\cal S}: {\cal S}\rightarrow D$ respects the additive structure of the state space. The state $s_1$ is mapped to a right-moving wave in the domain of application, and the state $s_2$ is mapped to a left-moving wave. Then $s_1+s_2$ is mapped to a standing wave.

Symmetry, Duality, and Theoretical Equivalence

The work draws a precise analogy between symmetry (automorphisms of a single model) and duality (isomorphisms between models), but emphasizes that duality is not reducible to gauge symmetry. The authors classify symmetries into stipulated, accidental, and proper symmetries of models, and analyze how these interact with duality mappings.

A central philosophical and technical issue is the relationship between duality and theoretical equivalence. The authors argue that duality, as a formal isomorphism, does not guarantee physical equivalence unless the interpretation maps commute with the duality (i.e., the duals are internally interpreted to the same domain). This is illustrated with examples such as Kramers-Wannier duality, where dual models at high and low temperature are formally dual but physically inequivalent due to external standards (e.g., temperature measurement).

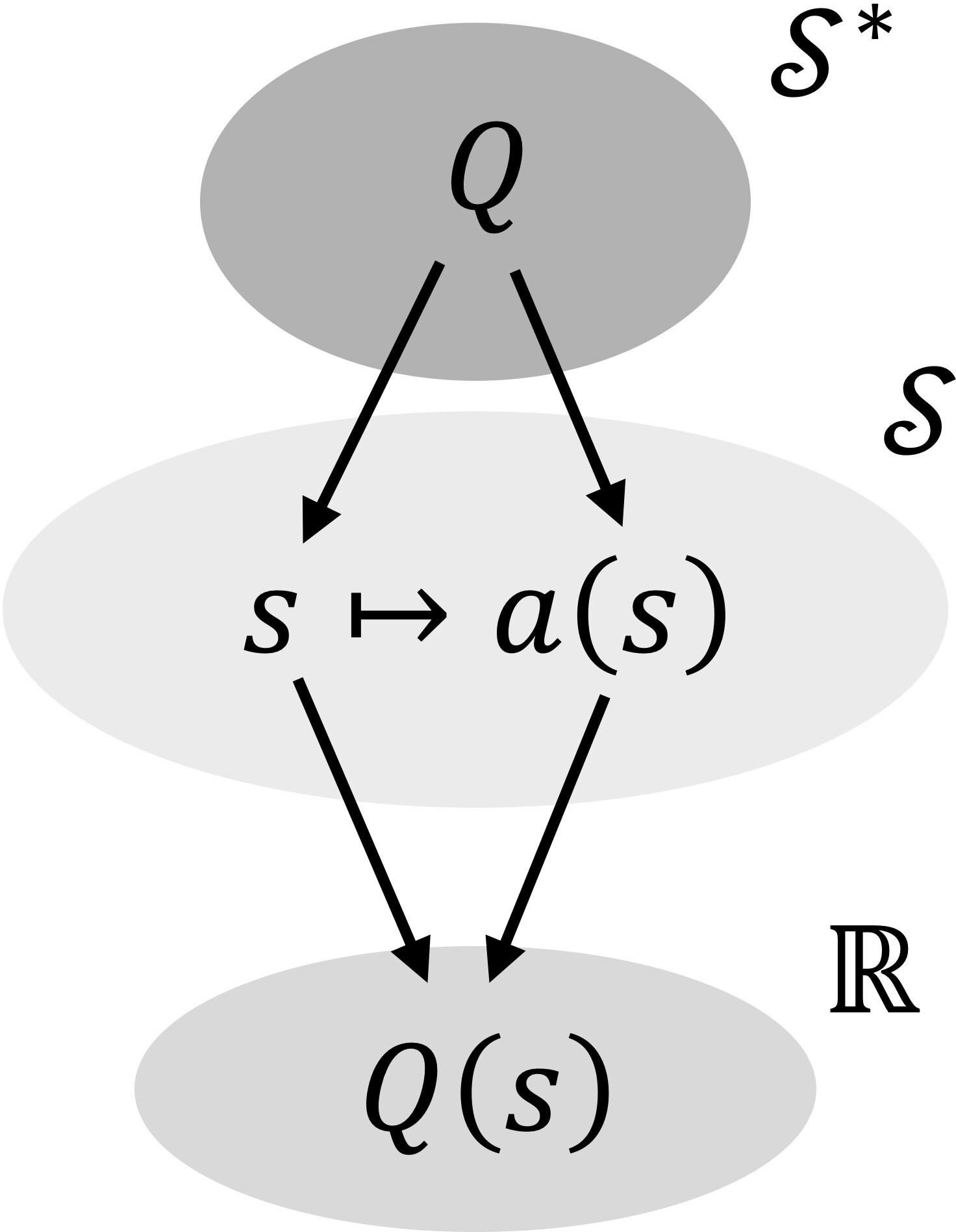
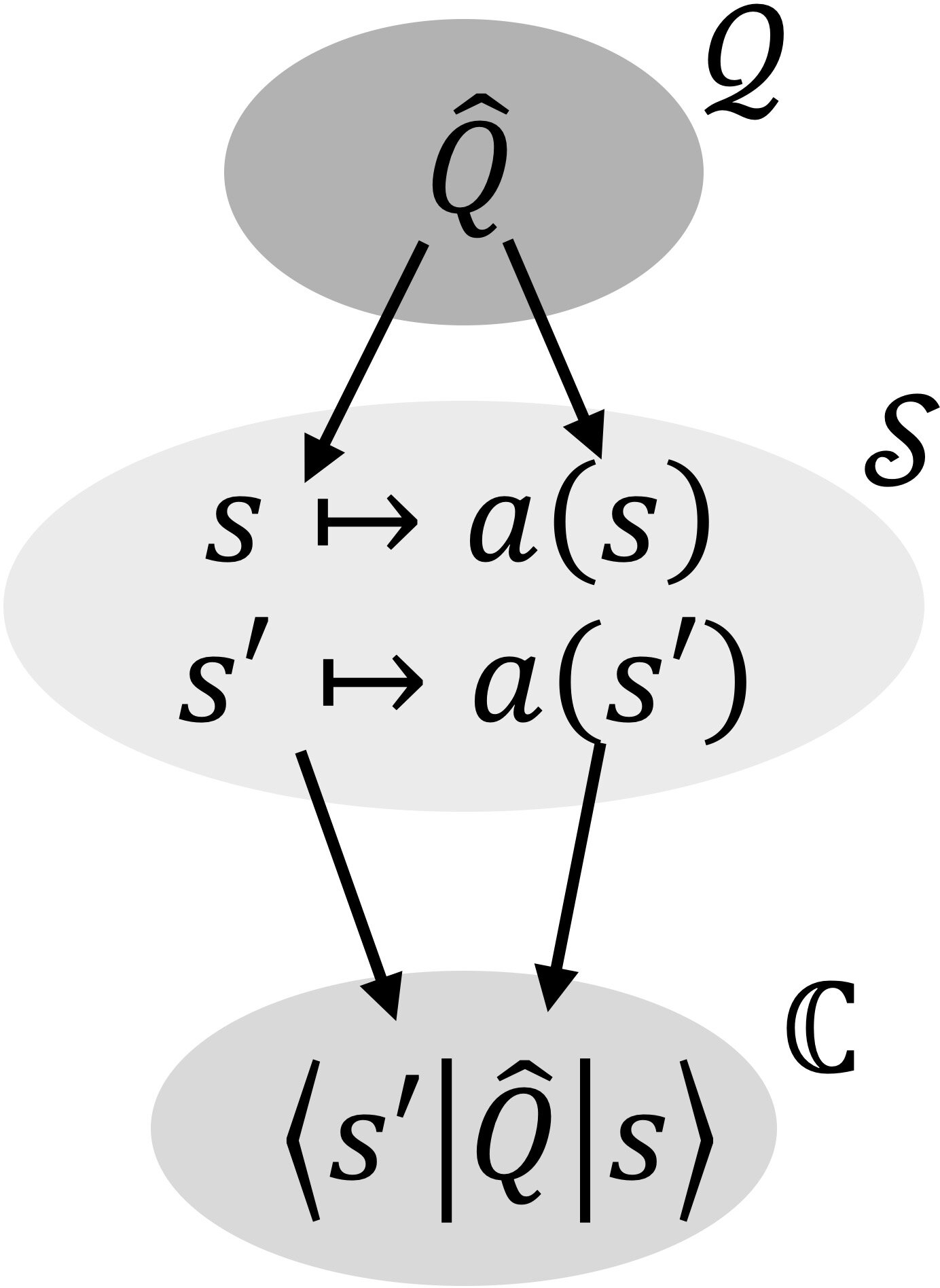
Figure 4: Preservation of values: (a) Left: classical possessed or quantum expectation value. (b) Right: matrix elements, for quantum theories.

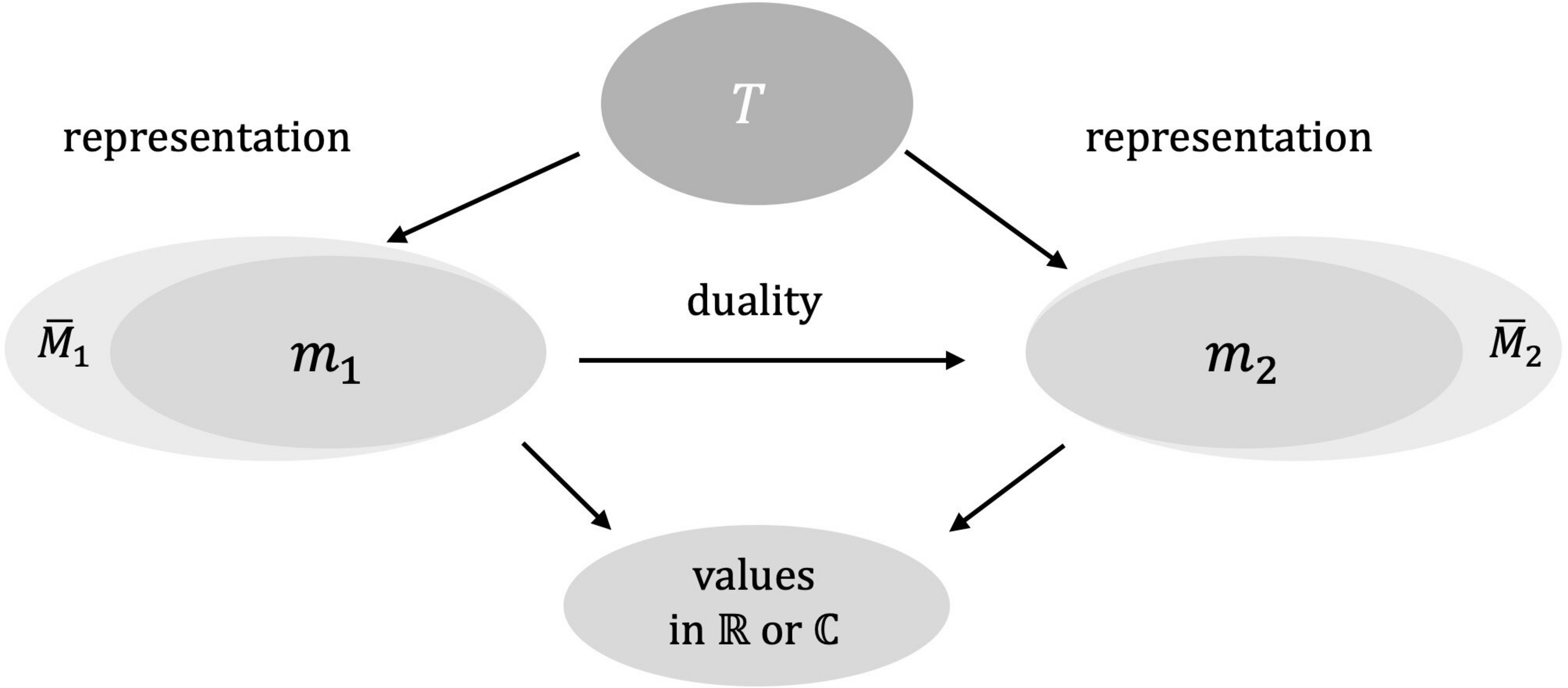
Figure 5: Relation between the bare theory "above" and its two duals, as representations, "below". The duality maps one model into the other. The isomorphism preserves the values of quantities.

Case Studies and Examples

The authors provide detailed technical analyses of canonical dualities:

• Position-Momentum Duality: The Fourier transform implements a unitary equivalence between the position and momentum representations of quantum mechanics, mapping operators and states such that all expectation values are preserved. This is a paradigmatic case of the Schema.
• Kramers-Wannier Duality: The duality between high- and low-temperature regimes in the 2D Ising model is formalized as an isomorphism of partition functions and correlation functions, but the physical inequivalence is manifest when external standards (e.g., thermometer readings) are considered.
• Gauge/Gravity Duality: The AdS/CFT correspondence is analyzed as a duality between a gravitational theory in $D$ dimensions and a conformal field theory in $D-1$ dimensions, with the duality mapping bulk fields to boundary operators and matching partition functions and correlation functions.

  Figure 6: Position and momentum operators, and their representations. Top row: representation-independent operators, ${\bf\hat X}$ and ${\bf\hat P}$. Middle row: model in the position representation, $M_x$. Bottom row: model in the momentum representation.

  

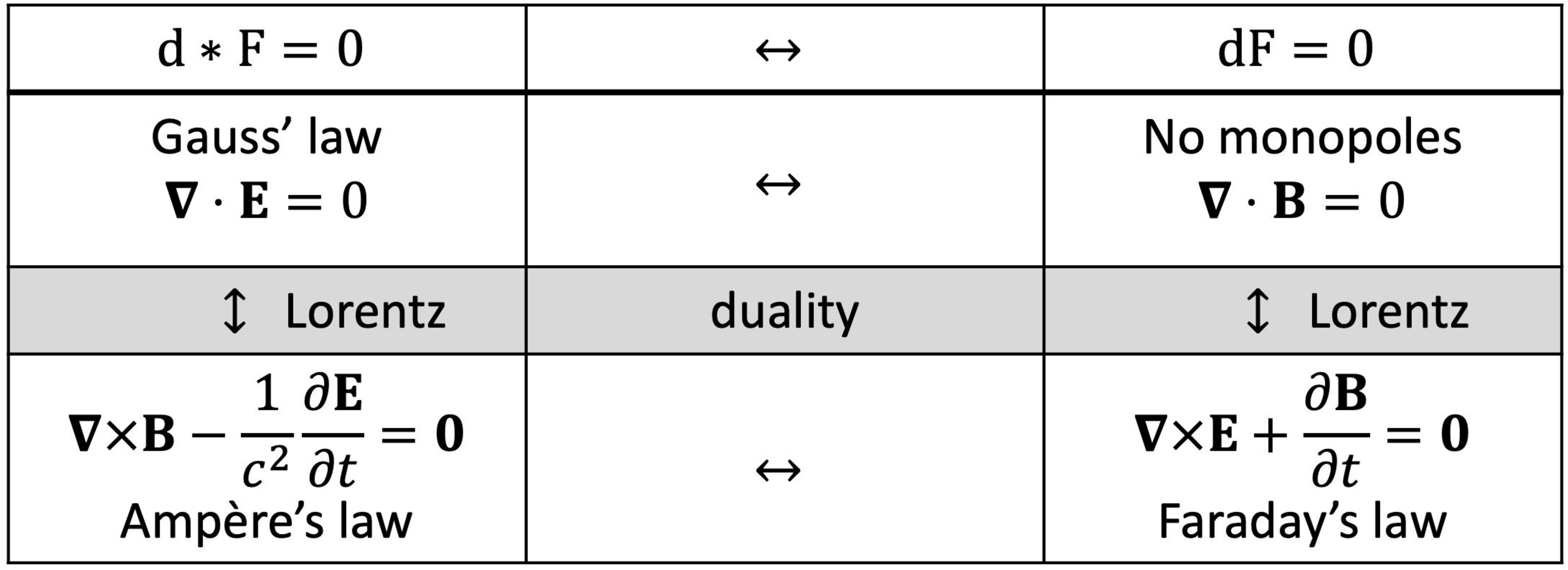
  Figure 7: Maxwell's equations and how they are mapped under Lorentz transformations (vertical arrows) and duality (horizontal arrows). Lorentz transformations generate linear transformations of equations along the vertical direction; duality transformations exchange equations along the horizontal direction. The analogy is complete if the duality group SO(2), which generates linear combinations of dual equations, acts along the horizontal direction.

Philosophical Implications and Theoretical Developments

The analysis has several important implications:

• Non-Automatic Equivalence: Duality does not entail theoretical or physical equivalence unless interpretative conditions are met. This is a strong claim, contradicting some positions in the literature that treat duality as sufficient for equivalence.
• Structured View of Theories: The Schema supports a "structured" (as opposed to "flat") conception of theories, where the common core and its models are related by explicit representation maps, and the structure to be preserved is made precise.
• Heuristic and Practical Roles: Beyond formal equivalence, dualities serve as heuristic tools for theory construction, unification, and the discovery of new physical mechanisms (e.g., the use of dualities in string theory to conjecture the existence of M-theory).
• Emergence and Theory Space: The work anticipates a geometric view of theory space, where different dual models correspond to different patches or limits, and the full theory may not be accessible from any single model.

  Figure 8: Plan of the book and its three Parts. The arrows on the left propose a reading sequence for philosophy readers, and on the right for physics readers. We expect philosophy of physics readers to be in a superposition of two "timelines". Solid lines indicate recommended Chapters. Broken lines indicate Chapters that readers may wish to skim through, depending on their interests.

Future Directions

The formal Schema and its philosophical analysis open several avenues for further research:

• Extension to Non-Triple Formulations: The Schema is generalized to models formulated via partition functions or path integrals, but further work is needed to systematize dualities in non-triple (e.g., categorical or homotopical) frameworks.
• Automated Duality Detection: The explicit formalism suggests the possibility of algorithmic or AI-assisted identification of dualities in large classes of physical theories, especially in high-dimensional or non-perturbative regimes.
• Interpretation and Realism: The distinction between internal and external interpretations provides a framework for analyzing underdetermination and scientific realism in the context of dualities, with potential applications to debates over the ontology of spacetime and quantum gravity.
• Heuristic Use in Model Building: The practical function of dualities in suggesting new theories or unifying frameworks (e.g., the M-theory program) remains a fertile area for both technical and philosophical investigation.

Conclusion

This work provides a rigorous, technically precise, and philosophically sophisticated account of duality in physics. By formalizing duality as an isomorphism of models with respect to a common core, and by distinguishing between formal, interpretative, and heuristic roles, the authors clarify both the power and the limitations of dualities in theory construction and interpretation. The Schema is robust across a wide range of physical theories and provides a foundation for future developments in both the formal and philosophical analysis of duality.