A Universal Banach--Bregman Framework for Stochastic Iterations: Unifying Stochastic Mirror Descent, Learning and LLM Training (2509.14216v1)

Abstract: Stochastic optimization powers the scalability of modern artificial intelligence, spanning machine learning, deep learning, reinforcement learning, and LLM training. Yet, existing theory remains largely confined to Hilbert spaces, relying on inner-product frameworks and orthogonality. This paradigm fails to capture non-Euclidean settings, such as mirror descent on simplices, Bregman proximal methods for sparse learning, natural gradient descent in information geometry, or Kullback--Leibler-regularized LLM training. Unlike Euclidean-based Hilbert-space methods, this approach embraces general Banach spaces. This work introduces a pioneering Banach--Bregman framework for stochastic iterations, establishing Bregman geometry as a foundation for next-generation optimization. It (i) provides a unified template via Bregman projections and Bregman--Fejer monotonicity, encompassing stochastic approximation, mirror descent, natural gradient, adaptive methods, and mirror-prox; (ii) establishes super-relaxations ($\lambda > 2$) in non-Hilbert settings, enabling flexible geometries and elucidating their acceleration effect; and (iii) delivers convergence theorems spanning almost-sure boundedness to geometric rates, validated on synthetic and real-world tasks. Empirical studies across machine learning (UCI benchmarks), deep learning (e.g., Transformer training), reinforcement learning (actor--critic), and LLMs (WikiText-2 with distilGPT-2) show up to 20% faster convergence, reduced variance, and enhanced accuracy over classical baselines. These results position Banach--Bregman geometry as a cornerstone unifying optimization theory and practice across core AI paradigms.

• The paper presents a universal framework that rigorously extends stochastic optimization to arbitrary Banach spaces using Bregman geometry and super-relaxation regimes.
• It unifies methods like stochastic mirror descent, adaptive algorithms (AdaGrad, RMSProp), and natural gradient descent under a common theoretical and algorithmic umbrella.
• Empirical results demonstrate up to 20% faster convergence, reduced variance, and improved accuracy across applications ranging from sparse learning to LLM training.

A Universal Banach–Bregman Framework for Stochastic Iterations: Unifying Stochastic Mirror Descent, Learning, and LLM Training

Motivation and Theoretical Foundations

The paper introduces a comprehensive Banach–Bregman framework for stochastic optimization, generalizing classical Hilbert-space methods to arbitrary Banach spaces via Bregman geometry. This extension is critical for modern learning paradigms where non-Euclidean geometries are intrinsic, such as mirror descent on probability simplices, Bregman proximal methods for sparse learning, natural gradient descent in information geometry, and KL-regularized training for LLMs. The framework leverages Bregman projections and Bregman–Fejér monotonicity, providing a unified template for stochastic approximation, mirror descent, natural gradient, adaptive methods (AdaGrad, RMSProp), and mirror-prox algorithms.

A central theoretical contribution is the rigorous justification of super-relaxation regimes ($\lambda_n > 2$) in non-Hilbert settings, extending the classical relaxation bounds and elucidating their acceleration effects. The analysis yields general convergence theorems, including almost-sure boundedness, weak and strong convergence, and geometric rates under minimal assumptions. The framework subsumes stochastic fixed-point iterations, monotone operator methods, and variational inequalities, with all convergence results stated in terms of Bregman distances and projections.

Algorithmic Instantiations

The abstract stochastic iteration is formalized as follows:

• Iterates $G_n$ are updated via Bregman-gradient steps in Banach spaces, with stochasticity in gradients, relaxations, and error tolerances.
• The update rule is $$\nabla \phi(G_{n+1}) = \nabla \phi(G_n) - \lambda_n U_n u_n^*$$, where $\phi$ is a Legendre potential, $u_n^*$ is a stochastic subgradient, and $U_n$ encodes step-size and feasibility information.
• The framework accommodates random relaxations, super-relaxations, and error terms, with factorization properties under independence assumptions.

Key algorithmic instantiations include:

• Stochastic Mirror Descent (SMD): Generalizes SGD to arbitrary Bregman geometries, with convergence guarantees under relative smoothness and strong convexity.
• Over-Relaxed SMD: Dual and KM-type over-relaxations ($\lambda_n \in (1,2)$) accelerate convergence and improve final loss, as shown in empirical results.

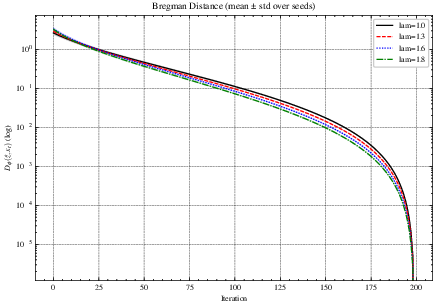
Figure 1: SMD vs. OR-SMD (mean$\pm$std over 5 seeds). Left: training loss (log-scale). Right: Bregman distance $D_\phi(\hat z, x_t)$ (log-scale). OR-SMD accelerates early progress and improves final loss.

• Adaptive Methods (AdaGrad, RMSProp): Realized as Bregman iterations in KL geometry, with adaptive step-sizes and stability guarantees. Over-relaxed variants further enhance convergence and variance reduction.

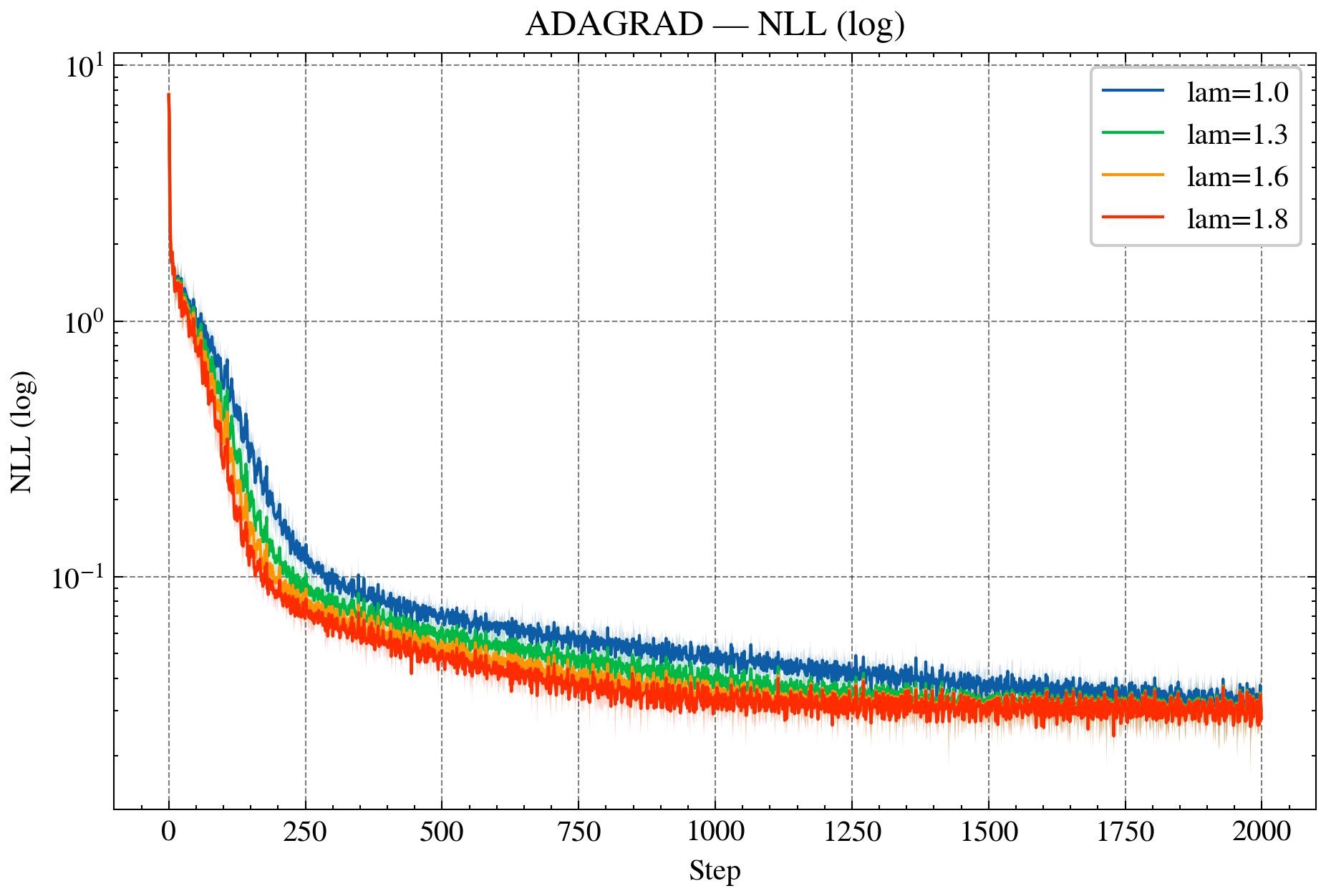
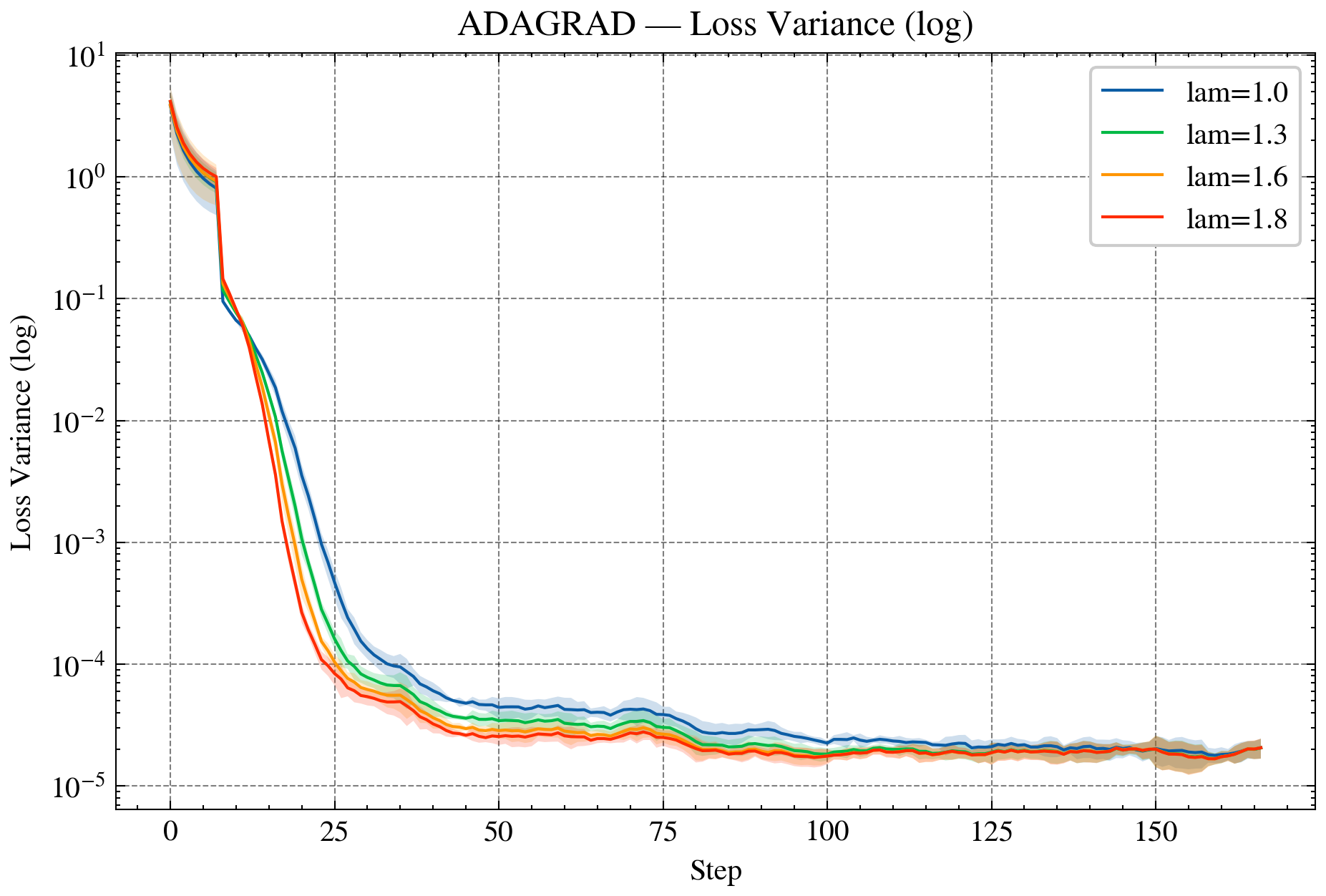
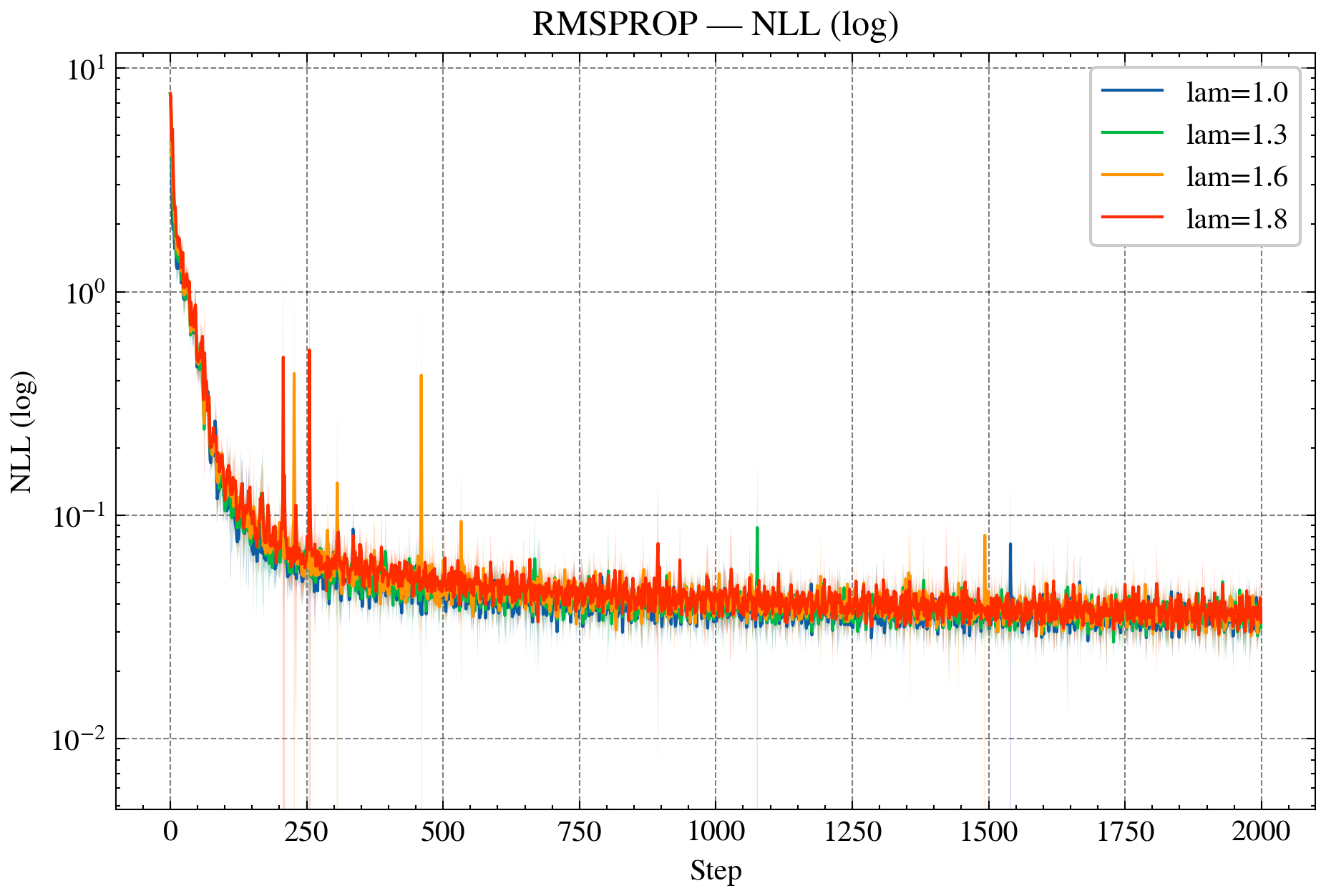
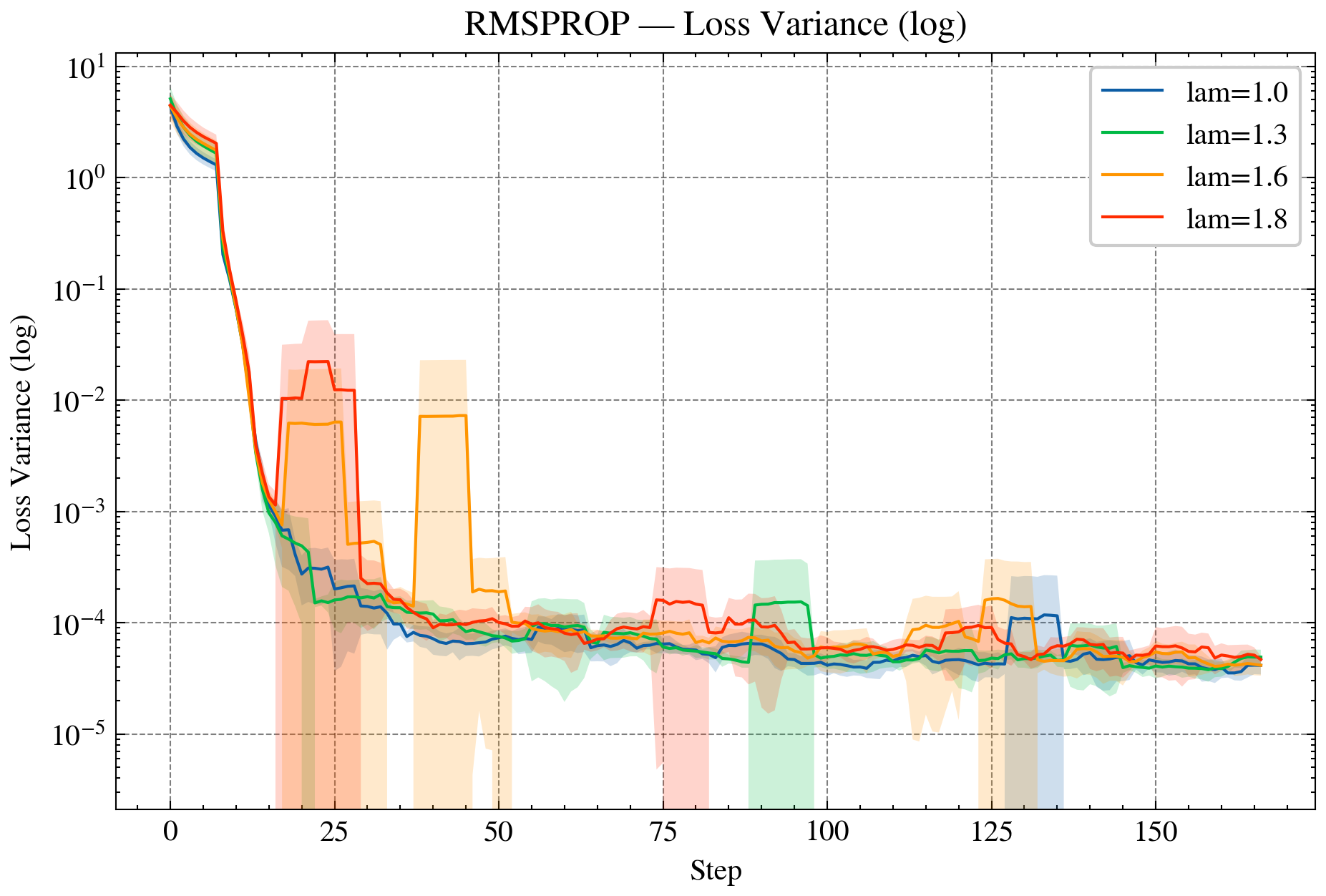
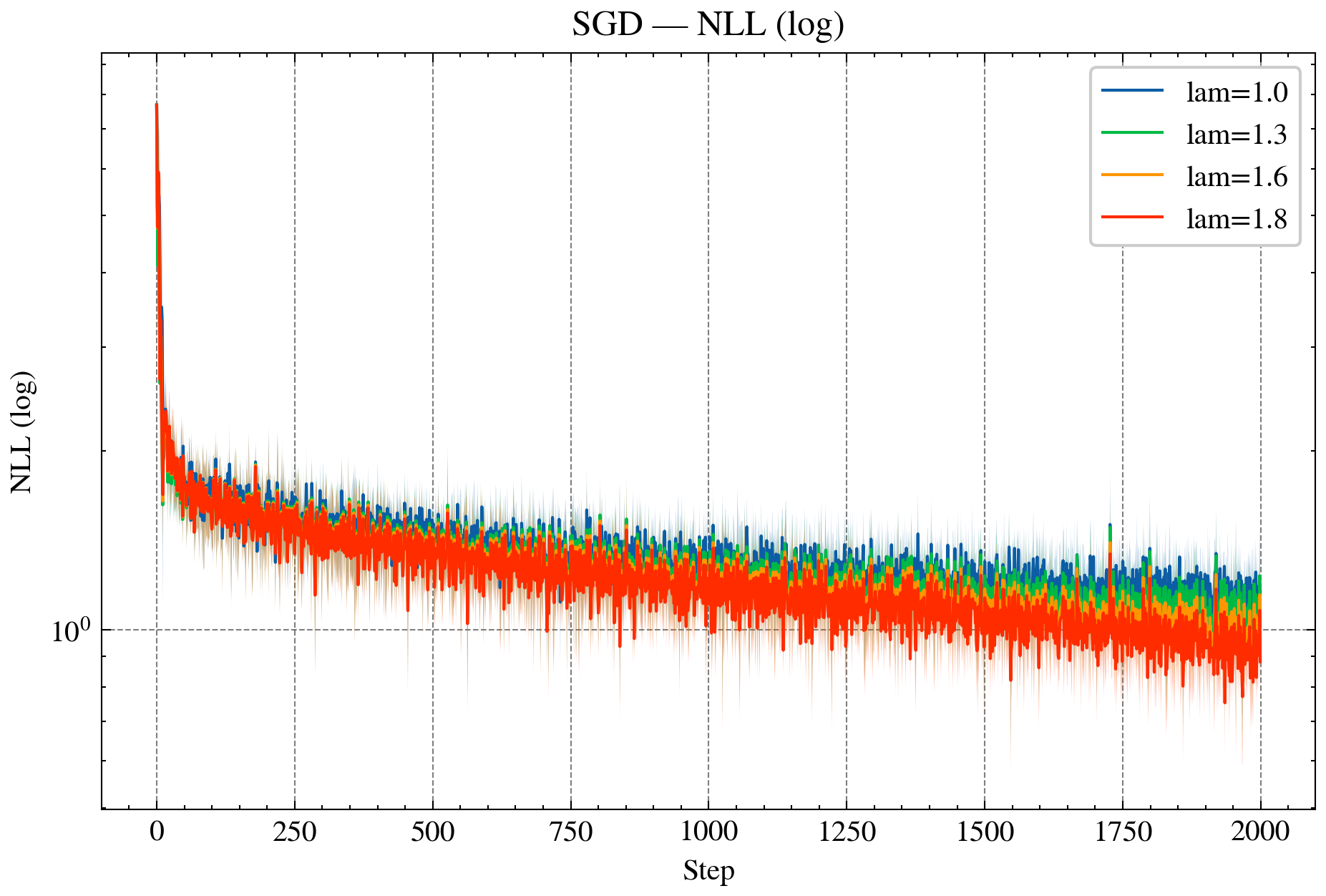
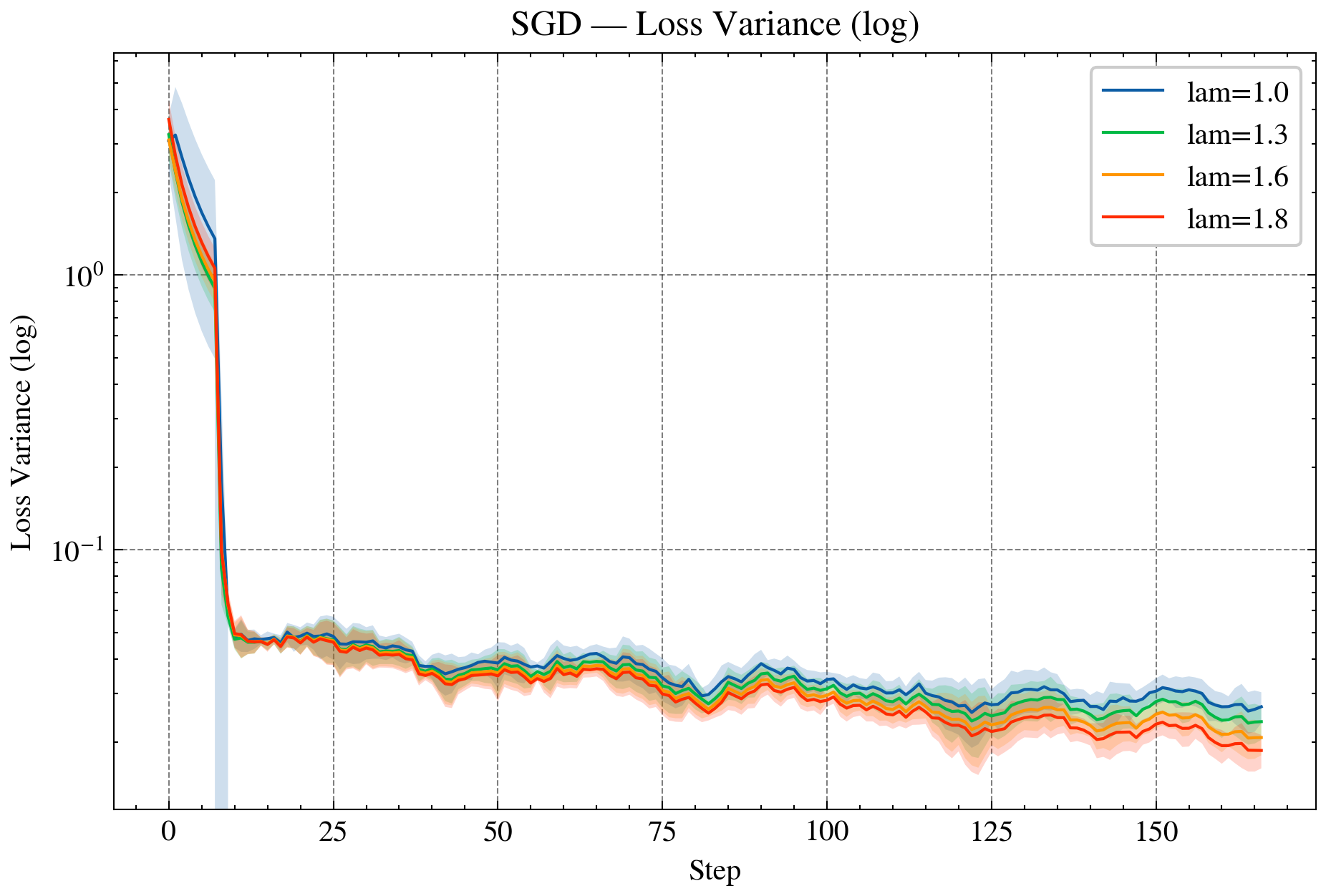
Figure 2: AdaGrad—NLL curves for standard and over-relaxed variants, demonstrating accelerated convergence and reduced variance.

• Natural Gradient Descent: Interpreted as SMD in information geometry, with Fisher-matrix preconditioning and over-relaxation for improved rates.
• Mirror-Prox: Generalizes monotone operator methods and variational inequalities to Banach–Bregman settings, supporting stochastic and over-relaxed updates.

Empirical Validation

The framework is validated across diverse learning paradigms:

• Machine Learning (Sparse Learning): Bregman–proximal SGD achieves strong convergence for regularized ERM in Banach spaces, with geometric rates under relative strong convexity.
• Deep Learning (Transformers): SMD and AdaGrad in KL geometry stabilize cross-entropy training on the probability simplex, with over-relaxation yielding faster convergence and improved accuracy.
• Reinforcement Learning: Mirror-Prox and KL-constrained policy gradient methods are unified under Bregman geometry, supporting entropy regularization and RLHF objectives.
• LLMs: SMD, AdaGrad, and RMSProp in KL geometry accelerate LLM training, with over-relaxed variants consistently reducing NLL, perplexity, and update variance.

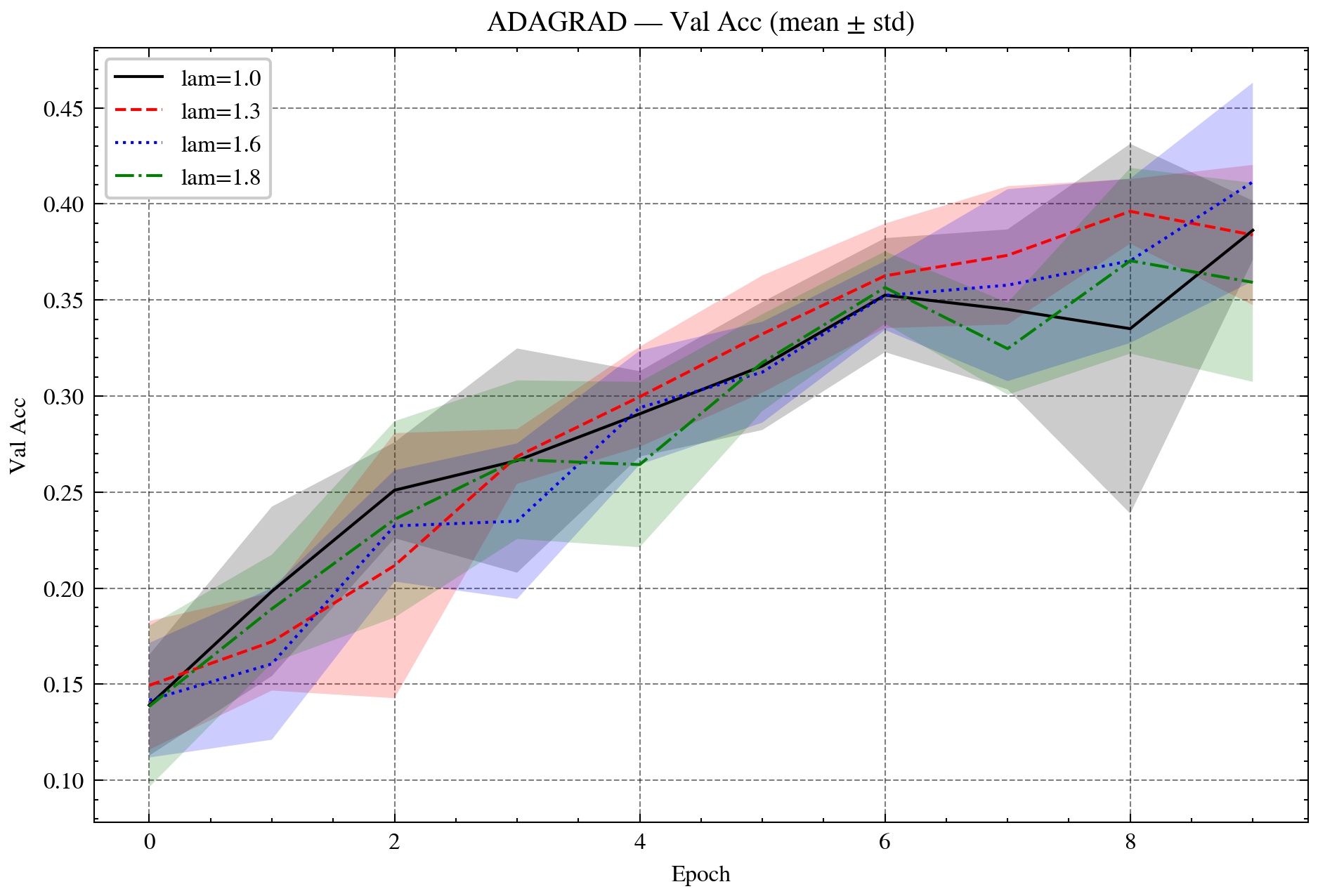
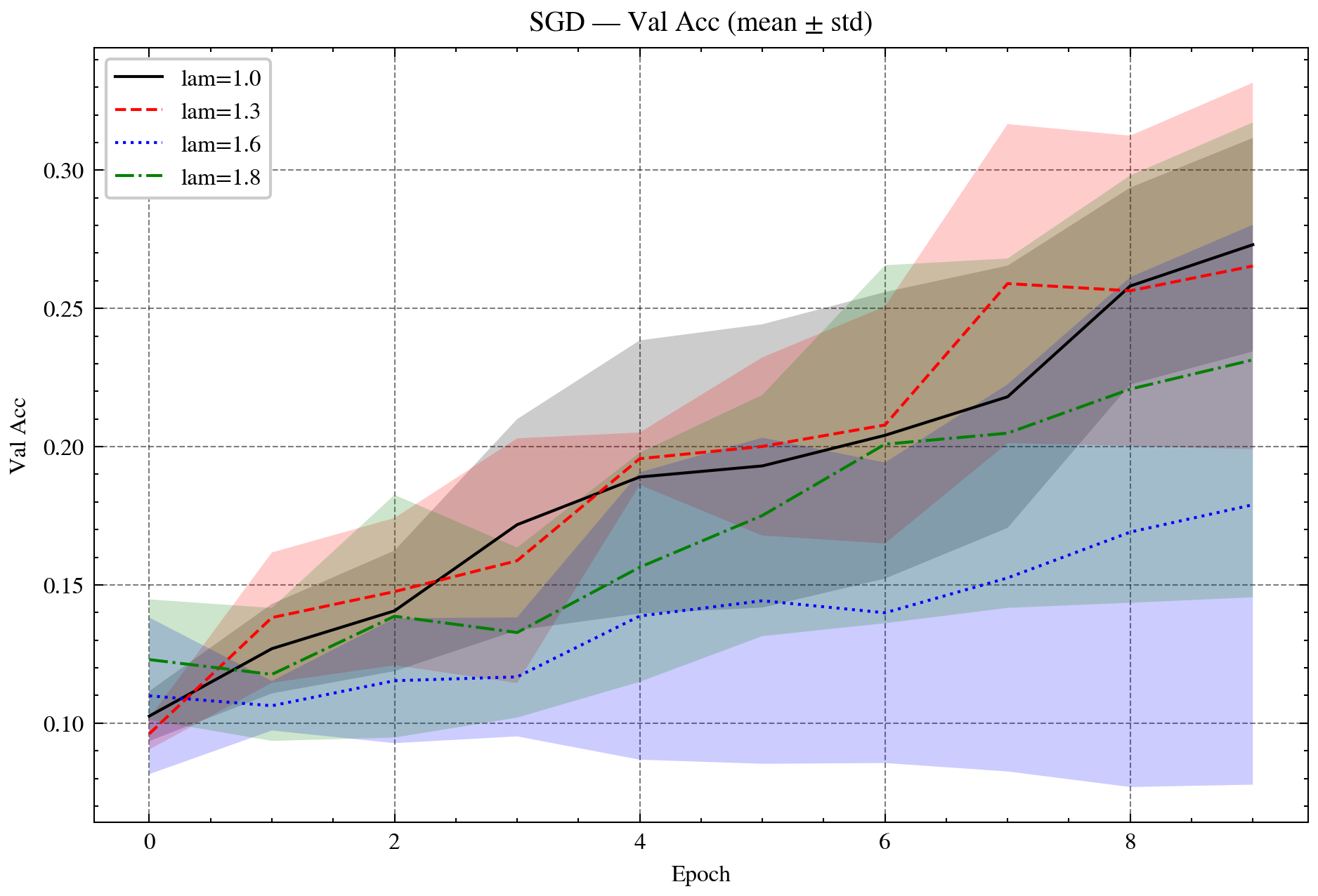
Figure 3: Validation accuracy on CIFAR-10 with ResNet-18. Left: AdaGrad vs. OR-AdaGrad. Right: SGD vs. OR-SGD. OR methods accelerate convergence and improve accuracy.

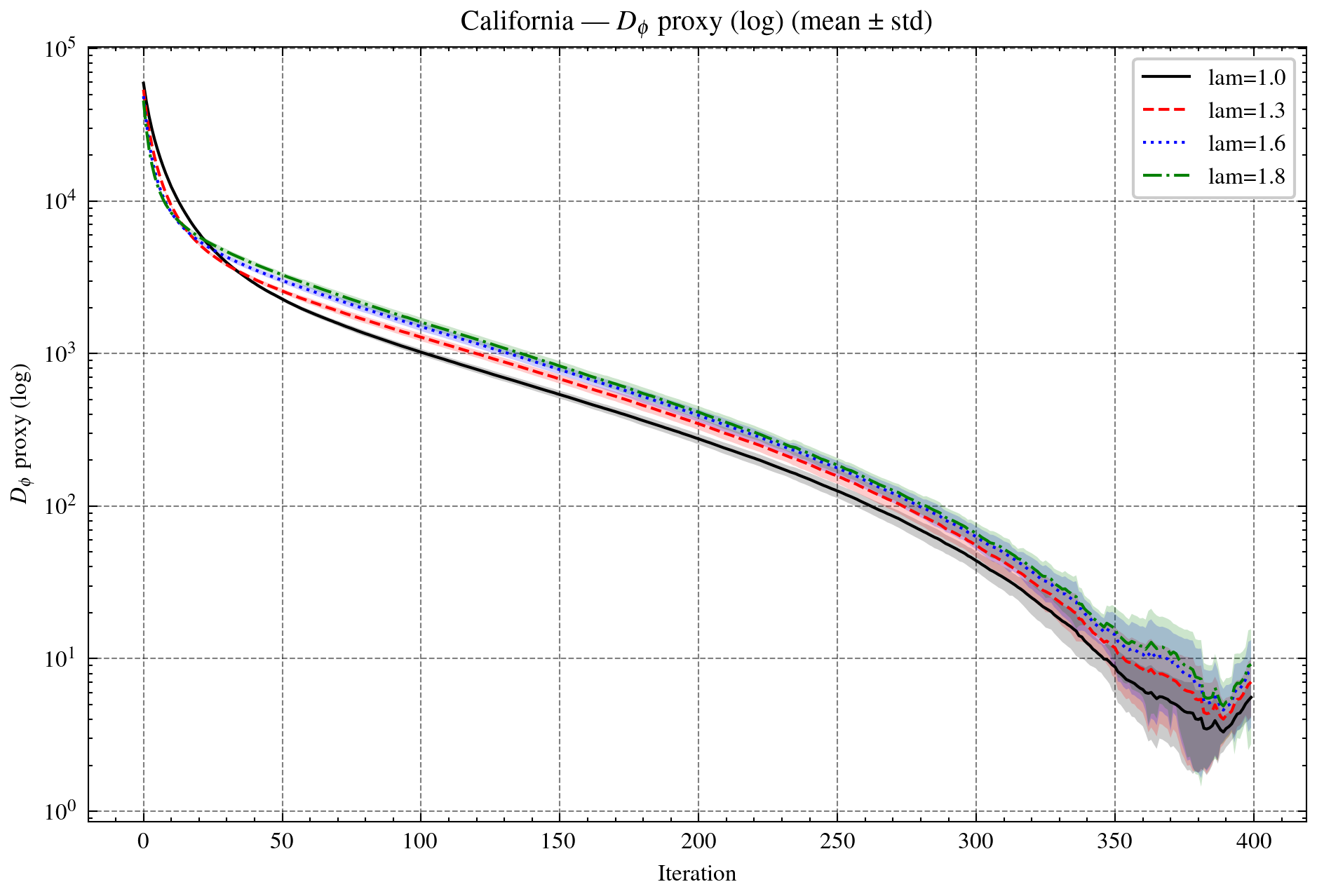
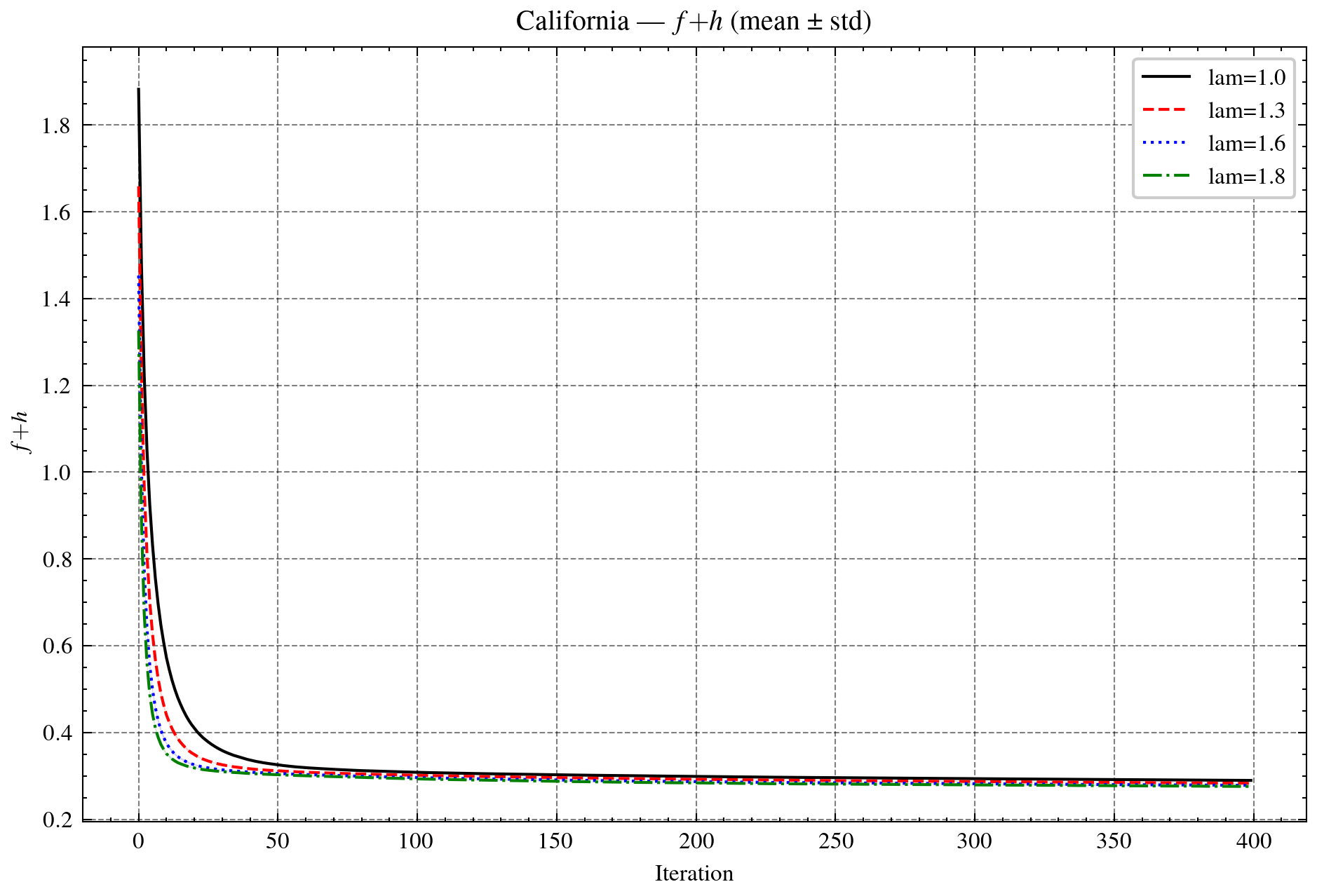
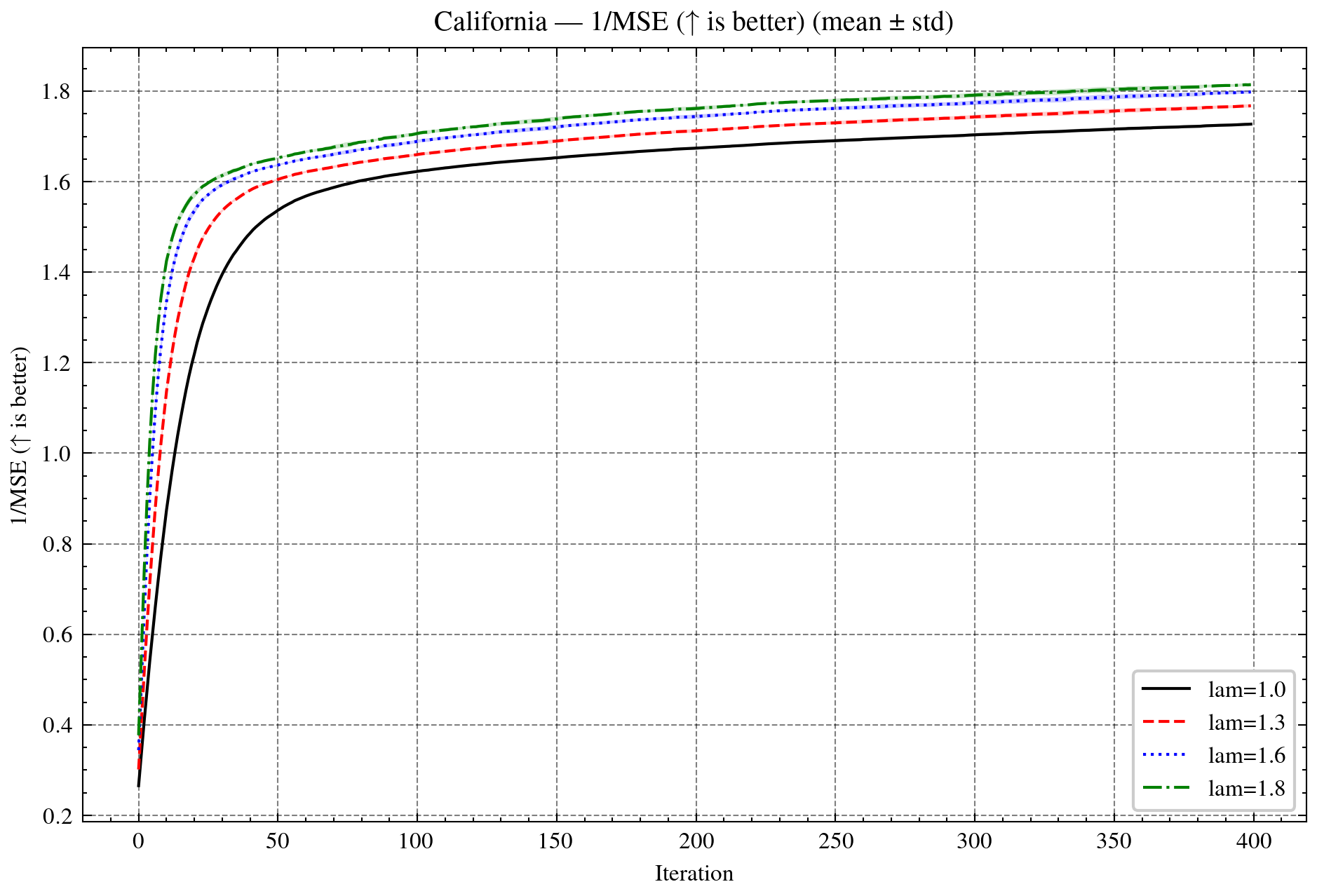
Figure 4: Sparse learning on California housing regression. Top: $D_\phi$ proxy (log-scale) and objective $f+h$. Bottom: sparsity ratio and validation error (1/MSE).

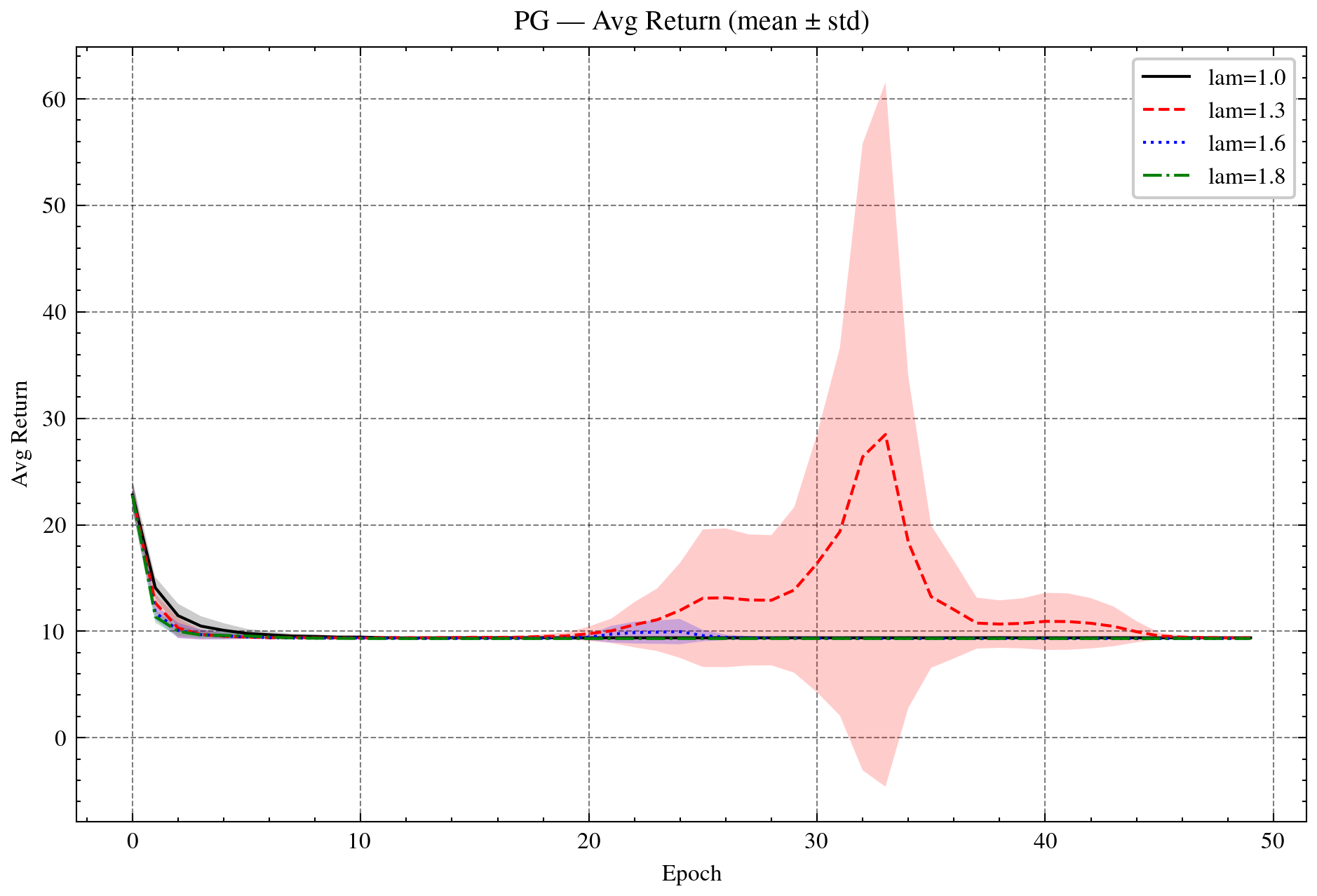
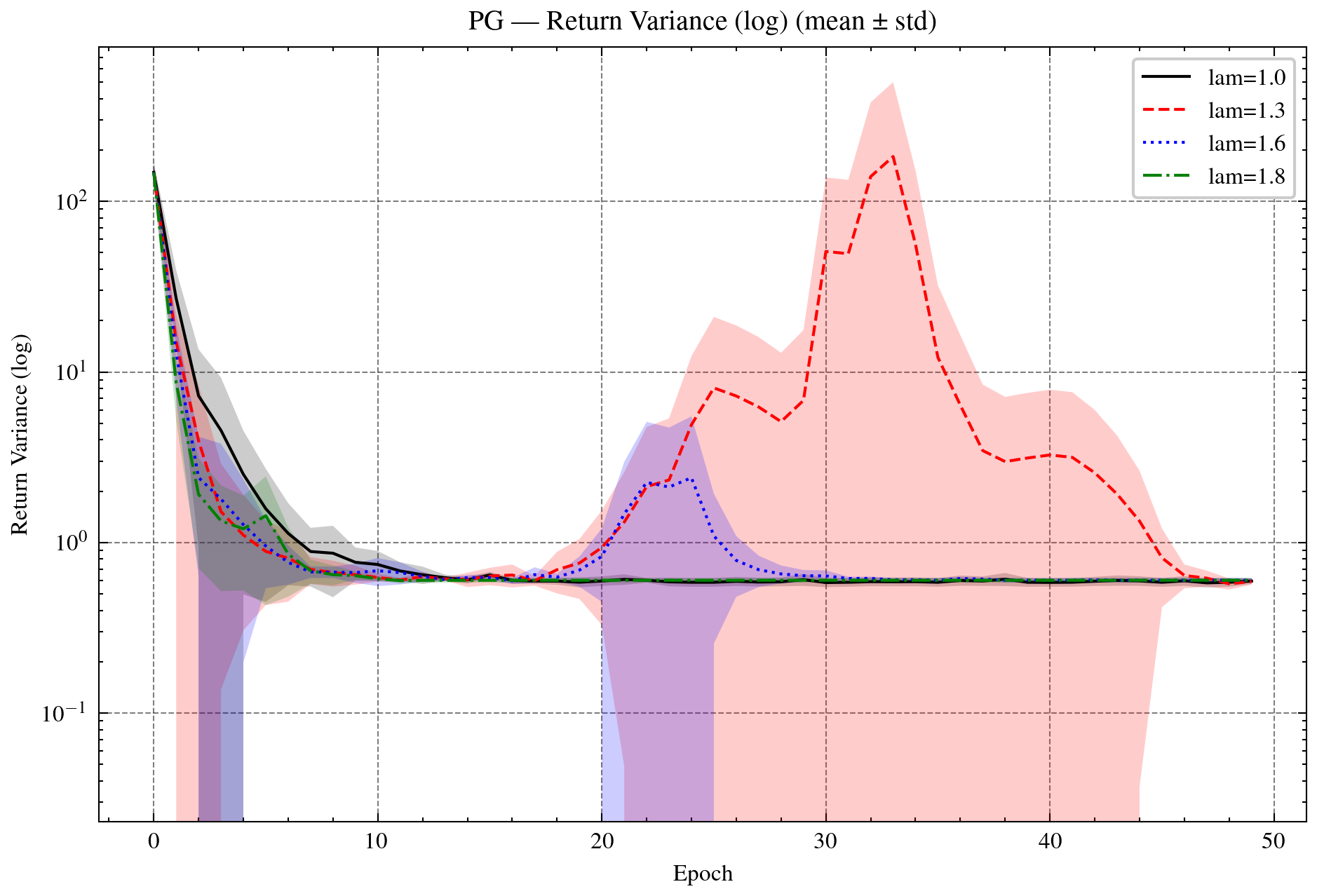
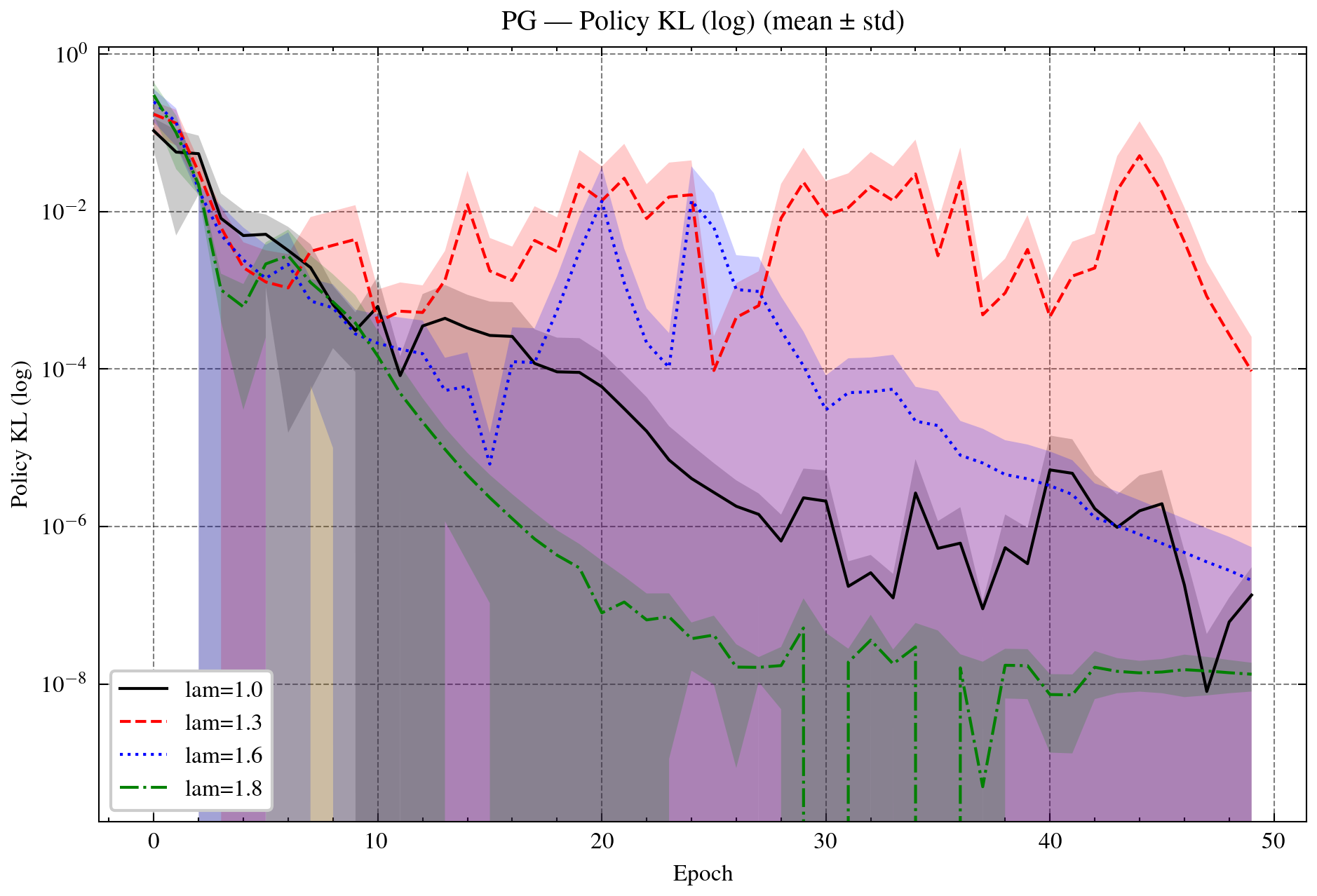
Figure 5: Policy gradient (PG) and Mirror-Prox (MP) with OR. Top: PG returns and variances. Bottom: PG and MP policy KL. OR-$\lambda=1.8$ provides the best stability while maintaining efficient KL reduction.

Numerical results highlight up to 20% faster convergence, reduced variance, and improved accuracy over classical baselines. Over-relaxation ($\lambda \in (1,2)$) consistently accelerates early progress and lowers final loss, with variance remaining stable across relaxation regimes.

Implications and Future Directions

The Banach–Bregman framework fundamentally extends the scope of stochastic optimization, enabling principled analysis and design of algorithms in non-Euclidean geometries. The rigorous justification of super-relaxation regimes ($\lambda_n > 2$) in Banach spaces is a strong claim, contradicting the classical Hilbert-space bound and explaining empirical acceleration effects. The unification of stochastic approximation, mirror descent, natural gradient, adaptive methods, and mirror-prox under a single analytical umbrella provides a robust foundation for scalable AI systems.

Practical implications include:

• Algorithmic Design: Practitioners can select Bregman potentials tailored to problem geometry (e.g., negative entropy for probability simplex, $\ell_1$ for sparsity), enabling efficient and stable optimization in high-dimensional, structured domains.
• Adaptive and Over-Relaxed Schedules: Over-relaxation and adaptive step-size schedules can be systematically incorporated, with theoretical guarantees for convergence and acceleration.
• Generalization to Finsler and Wasserstein Geometries: The framework is extensible to variable-metric (Finsler) and distributionally robust (Wasserstein) settings, supporting robust learning and KL-regularized RLHF.

Theoretically, the framework opens avenues for:

• Unified Analysis of Modern Learning Paradigms: Machine learning, deep learning, reinforcement learning, and LLM training can be analyzed through a shared geometric lens, facilitating cross-paradigm insights and transfer.
• Extensions to Robust and Distributionally Robust Optimization: Incorporation of Wasserstein and KL divergences enables robust learning under distribution shift and adversarial perturbations.

Conclusion

This work establishes Banach–Bregman geometry as a cornerstone for next-generation stochastic optimization, transcending Hilbert-space limitations and unifying theory and practice across core AI paradigms. The framework rigorously justifies super-relaxation, delivers strong convergence guarantees, and demonstrates broad empirical gains in speed, stability, and accuracy. Immediate extensions include Finsler and Wasserstein geometries, robust RLHF, and holistic unification of learning paradigms. The Banach–Bregman approach provides both mathematical rigor and practical scalability for modern AI systems.