Geometric Uncertainty for Detecting and Correcting Hallucinations in LLMs (2509.13813v1)

Abstract: LLMs demonstrate impressive results across diverse tasks but are still known to hallucinate, generating linguistically plausible but incorrect answers to questions. Uncertainty quantification has been proposed as a strategy for hallucination detection, but no existing black-box approach provides estimates for both global and local uncertainty. The former attributes uncertainty to a batch of responses, while the latter attributes uncertainty to individual responses. Current local methods typically rely on white-box access to internal model states, whilst black-box methods only provide global uncertainty estimates. We introduce a geometric framework to address this, based on archetypal analysis of batches of responses sampled with only black-box model access. At the global level, we propose Geometric Volume, which measures the convex hull volume of archetypes derived from response embeddings. At the local level, we propose Geometric Suspicion, which ranks responses by reliability and enables hallucination reduction through preferential response selection. Unlike prior dispersion methods which yield only a single global score, our approach provides semantic boundary points which have utility for attributing reliability to individual responses. Experiments show that our framework performs comparably to or better than prior methods on short form question-answering datasets, and achieves superior results on medical datasets where hallucinations carry particularly critical risks. We also provide theoretical justification by proving a link between convex hull volume and entropy.

• The paper introduces a geometric framework that quantifies global and local uncertainty for detecting hallucinations in LLM responses.
• It computes geometric volume from response embeddings and employs local metrics like Archetype Rarity to rank response reliability.
• Empirical results on diverse datasets, including high-stakes medical data, demonstrate the framework’s effectiveness in reducing hallucinations.

Geometric Uncertainty for Detecting and Correcting Hallucinations in LLMs

Introduction

The paper "Geometric Uncertainty for Detecting and Correcting Hallucinations in LLMs" addresses the challenging problem of hallucinations in LLMs, where models generate incorrect yet plausible answers. It proposes a geometric framework for estimating both global and local uncertainty using only black-box access. This framework employs archetypal analysis to assess the semantic properties of model responses, offering methods to detect and mitigate hallucinations effectively.

Geometric Framework for Uncertainty

The proposed framework introduces a novel method for quantifying uncertainty in LLM responses by analyzing the geometric dispersion of response embeddings.

1. Global Uncertainty via Geometric Volume:
   • The concept of Geometric Volume measures the volume of the convex hull formed by a set of archetypes derived from response embeddings.
   • Archetypal analysis is applied to the responses, identifying extremal archetypes that span the embedding space, thus encapsulating the semantic boundaries of possible responses.

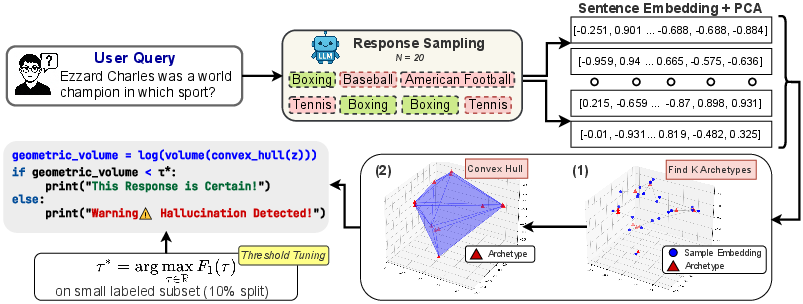
     Figure 1: A schematic of geometric volume: (1) sample $n$ responses from the LLM, (2) embed and apply dimensionality reduction, (3) perform archetypal analysis and compute the convex hull, and (4) apply a threshold to detect hallucination.

2. Local Uncertainty Detection:
   • Geometric Suspicion ranks responses based on their reliability by evaluating three metrics: Archetype Rarity, Average Distance to Nearest Neighbors, and Distance from Consensus.
   • This enables finer selection of high-fidelity responses in scenarios where hallucinations are possible.

     Figure 2: We demonstrate local uncertainty metrics using Archetype Rarity, Average Distance to Nearest Neighbors, and Distance from Consensus, which can transform hallucinated responses at temperature~0 into correct responses.

Methodology

The framework achieves uncertainty quantification through a detailed geometric analysis of response embeddings:

• Archetypal Analysis: Utilized to identify boundary archetypes in the embedding space, providing global semantic spread insights and local response diagnostics.
• Implementation Details:
  • Response embeddings are reduced in dimensionality and analyzed for their reconstruction from archetypes.
  • High Geometric Volume signals broader semantic spread, correlating to higher uncertainty.

Results and Performance

The geometric approach was tested on various datasets, including CLAMBER, TriviaQA, ScienceQA, MedicalQA, and K-QA, showing superior performance in hallucination detection, particularly in high-stakes medical datasets.

• Compared to methods like Semantic Volume and Semantic Entropy, the geometric framework delivered competitive or superior performance.
• It effectively reduced hallucination rates by employing local uncertainty metrics in a Best-of-N selection strategy.

Discussion

The key strength of the geometric framework lies in its ability to provide a nuanced understanding of response uncertainty. By connecting global dispersion with local response reliability, it presents a scalable solution adaptable to any LLM without requiring access to model internals. The results highlight potential avenues for integrating such geometric methods to enhance interpretability and decision-making in AI-driven applications.

Conclusion

The framework demonstrates that geometric properties of response embeddings can be leveraged to address hallucination issues in LLMs effectively. By offering both theoretical justification and empirical validation, it stands as a robust approach for hallucination detection and correction, paving the way for more reliable AI systems in critical domains.

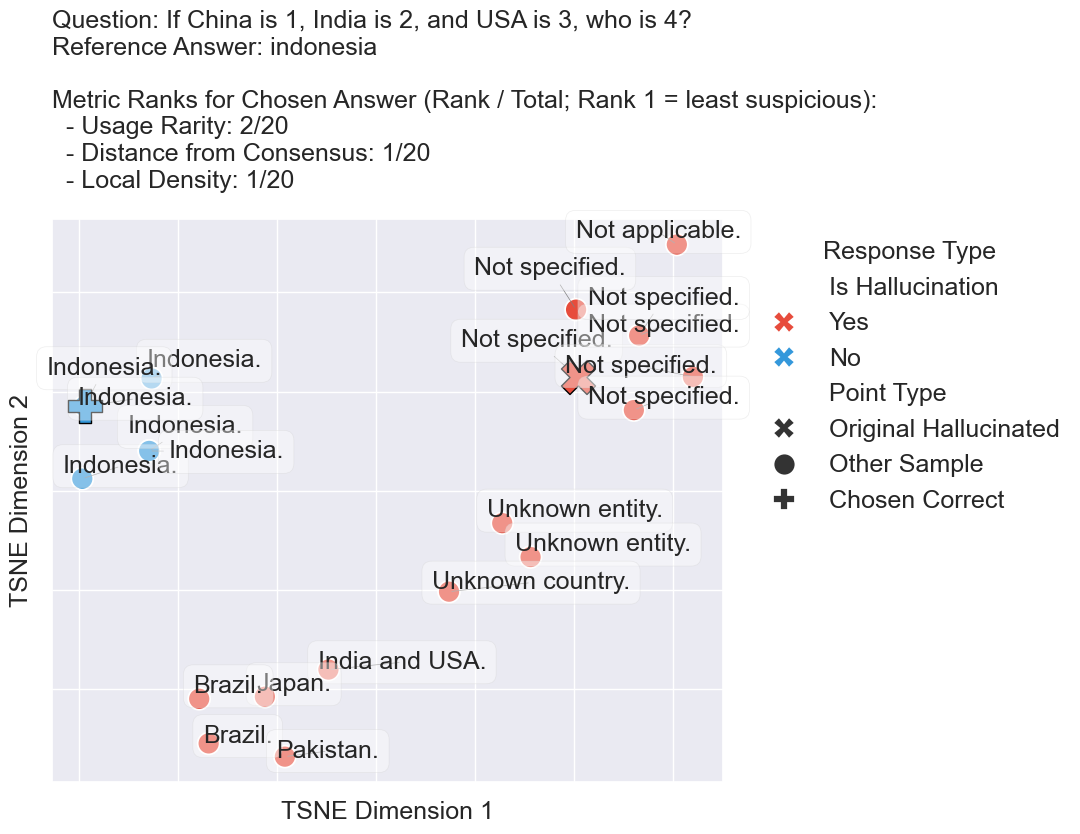
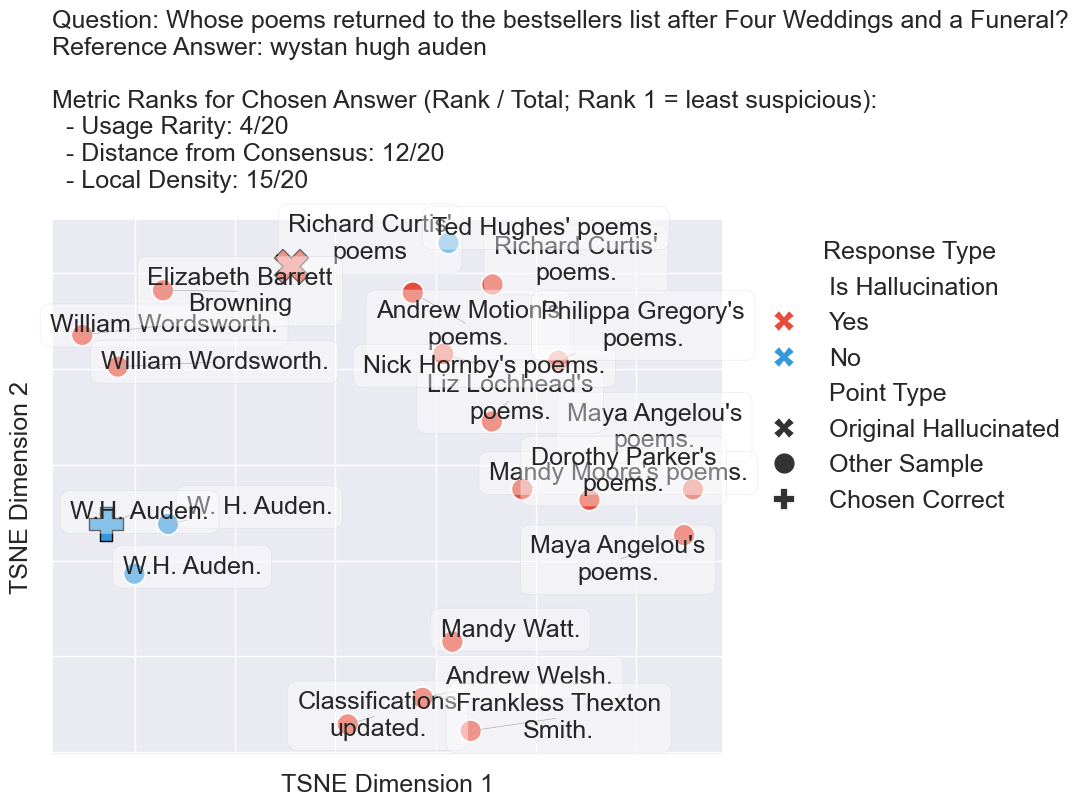
Figure 3: A low rank for each component

Future Work

Further exploration could refine the integration of geometric methods with model-specific enhancements, potentially incorporating them into model training or fine-tuning phases for even greater reliability and transparency in LLM outputs.