Demonstration of a Logical Architecture Uniting Motion and In-Place Entanglement: Shor's Algorithm, Constant-Depth CNOT Ladder, and Many-Hypercube Code (2509.13247v1)

Abstract: Logical qubits are considered an essential component for achieving utility-scale quantum computation. Multiple recent demonstrations of logical qubits on neutral atoms have relied on coherent qubit motion into entangling zones. However, this architecture requires motion prior to every entangling gate, incurring significant cost in wall clock runtime and motion-related error accumulation. We propose and experimentally realize an alternative architecture which unites qubit motion and in-place entanglement via nearest-neighbor gates. Our approach maintains all-to-all connectivity, while minimizing qubit motion overheads. We demonstrate three key results on Infleqtion's Sqale QPU, which hosts an array of 114 neutral atom qubits. First, we perform a logical qubit realization of a pre-compiled variant of Shor's Algorithm. We find better logical-than-physical performance over a range of settings including with loss correction and leakage detection. Second, we introduce a technique for performing CNOT ladders with depth independent of both the number of logical qubits N and the code distance d. In proof-of-principle experiments with 8 and 12 logical qubits, we find ~4x reduction in error via the logical encodings. Third, we experimentally realize initialization of the [[16, 4, 4]] many-hypercube QEC code. All three results benefit from optimized compilation via Superstaq, as well as our underlying architecture uniting motion and in-place entanglement. This architecture offers a path to reducing the overhead of utility-scale quantum applications relative to architectures based on entangling zones.

• The paper demonstrates integration of mid-circuit atom motion with in-place entanglement to execute a pre-compiled Shor’s algorithm and scalable logical operations.
• It employs constant-depth CNOT ladders using transversal gates, achieving reduced error rates independent of logical qubit count and code distance.
• It initializes the [[16,4,4]] many-hypercube code via recursive concatenation to showcase improved logical performance over unencoded circuits.

Logical Architecture for Neutral Atom Quantum Computing: Integrating Motion and In-Place Entanglement

Introduction

This work presents an experimental realization of a logical quantum computing architecture on neutral atom hardware that unifies mid-circuit atom motion with in-place, locally-addressed entangling gates. The architecture, implemented on Infleqtion’s Sqale QPU, is designed to maintain all-to-all connectivity while minimizing the overheads and error accumulation associated with frequent atom movement. The paper demonstrates three key primitives: (1) logical qubit execution of a pre-compiled Shor’s algorithm, (2) constant-depth CNOT ladders with depth independent of logical qubit number and code distance, and (3) initialization of the [[16,4,4]] many-hypercube code. These results are enabled by a combination of hardware capabilities—parallel atom motion, individual optical addressing, and non-destructive readout—and optimized compilation via Superstaq.

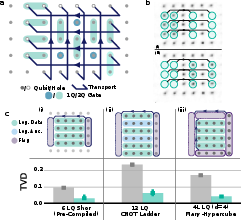
Figure 1: (a) Sqale's architecture, combining locally-addressed gates and mid-circuit rearrangement. (b) Fluorescence images before (top) and after (bottom) translating and stretching a 6-qubit block through interstitial lanes. (c) Summary of demonstrations in this work, including logical qubit layouts and encoded/unencoded performance in terms of TVD.

Architecture and Methods

The architecture leverages a 7×6 patch of a 114-qubit array, with sufficient site spacing to allow parallel, block-wise atom motion. This enables dynamic reconfiguration of connectivity mid-circuit, supporting both fault-tolerant logical state preparation (with flag qubits) and transversal entangling gates. After movement, entangling operations are performed in-place, avoiding the need for a dedicated entangling zone and thus reducing both runtime and motion-induced errors.

Logical qubits are encoded using the [[4,2,2]] CSS code and the [[16,4,4]] many-hypercube code. The [[4,2,2]] code, with distance $d=2$, supports transversal CNOTs and is used for both logical Shor and CNOT ladder circuits. The [[16,4,4]] code is constructed by concatenating the [[4,2,2]] code with itself, yielding a higher-distance code suitable for scalable error correction.

Post-processing includes atom loss detection, loss correction (by inferring missing codeword bits), logical decoding (including flag and codespace checks), and Pauli frame correction for constant-depth circuits. Leakage detection units (LDUs) are implemented via pairs of CNOTs targeting flag qubits, enabling circuit-based detection of non-computational leakage without hardware modification.

Noisy simulations are performed using Sqalesim, which models each atom as a five-level system (qubit subspace, two leakage states, and a loss state), with efficient Clifford simulation and Pauli twirling for non-Clifford operations. Atom motion is explicitly modeled as a source of phase errors.

Logical Shor’s Algorithm: Implementation and Results

The logical implementation of Shor’s algorithm uses pre-compiled circuits for order-finding with $N=15$ and $a=11$, reducing the circuit to a Hadamard test with a single controlled modular multiplier. Both two-row and three-row logical encodings are realized using [[4,2,2]] patches, with transversal gates and mid-circuit flag qubit movement to achieve the required connectivity.

Experimental results show a statistically significant reduction in total variation distance (TVD) between the measured and ideal output distributions for logical encodings compared to unencoded circuits. The three-row encoding, despite lower post-selection yield, achieves lower TVD than the two-row encoding, indicating enhanced error detection via distributed logical redundancy. The addition of LDUs does not improve TVD in this shallow circuit due to the overhead of extra two-qubit gates, but is expected to be beneficial in deeper circuits.

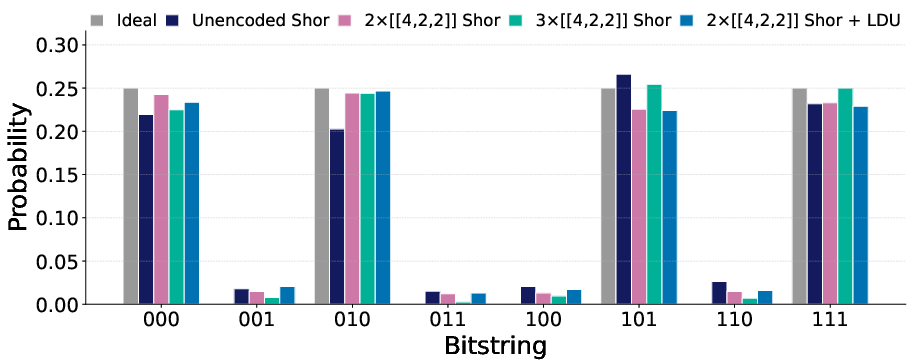
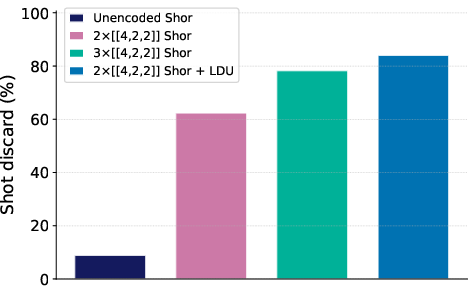
Figure 2: Experimental results for all Shor circuits: (a) measured probability distribution, (b) post-selection discard rates, and (c) TVD between experimental and ideal distributions. Diamonds indicate simulated TVD from Sqalesim.

Noisy simulations confirm that the logical circuits maintain lower TVD than unencoded circuits up to noise scaling factors of 3.5–4×, with the three-row encoding outperforming two-row across a broad noise regime. The LDU-equipped circuit exhibits a lower pseudothreshold due to the increased CZ gate count, highlighting the trade-off between error detection and circuit depth for low-distance codes.

Constant-Depth CNOT Ladders

The architecture supports constant-depth CNOT ladders, a key primitive for modular arithmetic and GHZ state preparation, by exploiting the commutativity and associativity of addition. The “outside-in” arrangement allows parallelization of CNOTs using nearest-neighbor connectivity, and logical encoding is achieved by mapping each row to a [[4,2,2]] patch.

By introducing ancilla logical qubits and using transversal gates, the depth of the CNOT ladder is rendered independent of both the number of logical qubits $N$ and the code distance $d$. Experimental results for 8 and 12 logical qubit ladders show a $\sim$4× reduction in error rate for encoded circuits compared to unencoded, with the improvement factor persisting as $N$ increases.

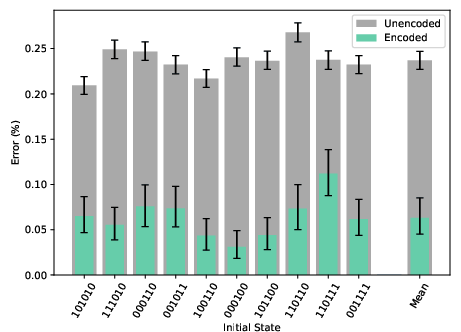
Figure 3: Error rates for unencoded (gray) vs encoded (green) constant-depth CNOT ladders with 8 logical qubits.

Figure 4: Error rates for unencoded (gray) vs encoded (green) constant-depth CNOT ladders with 12 logical qubits.

Simulations indicate that the encoded circuits outperform unencoded up to noise scaling factors of 9×, with the pseudothreshold decreasing as $N$ increases. The proportion of discarded shots due to flag qubit errors in state preparation dominates, and the shot budget required for large $N$ becomes significant, motivating the transition to higher-distance codes for scalability.

Many-Hypercube Code Initialization

The [[16,4,4]] many-hypercube code is prepared by recursively concatenating the [[4,2,2]] code. Five logical patches are initialized in the $\ket{00}_L$ state, with mid-circuit movement of flag qubits to complete fault-tolerant preparation. Logical state preparation is verified for multiple bitstrings, with encoded circuits achieving a mean error rate of 0.0421 compared to 0.1721 for unencoded, despite a lower post-selection yield due to loss detection.

Figure 5: Error rates for unencoded (gray) vs encoded (green) many-hypercube state preparation across various bitstrings.

Noisy simulations corroborate the experimental separation in error rates, though some system drift is observed. The results demonstrate the feasibility of initializing higher-distance codes on neutral atom hardware with logical performance advantages.

Architectural Implications and Scaling

The architecture is designed to minimize circuit depth and runtime by trading increased qubit count for reduced time costs, a favorable trade-off for neutral atom systems. For general CSS codes of arbitrary distance $d$, logical gate layers are shown to be measurement-bottlenecked rather than movement-bottlenecked for all relevant $d$, as the required logical movement per gate remains small.

Figure 6: Dominant time cost of a gate layer involving a transversal CNOT via movement for varying code distance and logical movement spaces.

Syndrome decoding is also manageable: the architecture’s use of constant, near-neighbor logical movement ensures that the number of logical qubits in the observing region after $O(d)$ rounds is at most $O(d^2)$, avoiding exponential slowdowns in decoding. This supports the viability of constant-depth logical architectures for large-scale, fault-tolerant quantum computation on neutral atom platforms.

Conclusion

This work demonstrates a logical quantum computing architecture on neutral atom hardware that integrates mid-circuit atom motion with in-place entanglement, enabling all-to-all connectivity with reduced motion overhead. Experimental results show improved logical-over-physical performance for pre-compiled Shor circuits, constant-depth CNOT ladders, and many-hypercube code initialization. The architecture is well-suited to the strengths of neutral atom systems, supporting constant-depth circuit paradigms and scalable error correction. Future developments, including dual-species arrays for in-place readout and further compiler optimizations, are expected to further reduce runtime and error, advancing the path toward large, fault-tolerant quantum computers.