Reversible Deep Equilibrium Models (2509.12917v1)

Abstract: Deep Equilibrium Models (DEQs) are an interesting class of implicit model where the model output is implicitly defined as the fixed point of a learned function. These models have been shown to outperform explicit (fixed-depth) models in large-scale tasks by trading many deep layers for a single layer that is iterated many times. However, gradient calculation through DEQs is approximate. This often leads to unstable training dynamics and requires regularisation or many function evaluations to fix. Here, we introduce Reversible Deep Equilibrium Models (RevDEQs) that allow for exact gradient calculation, no regularisation and far fewer function evaluations than DEQs. We show that RevDEQs achieve state-of-the-art performance on LLMling and image classification tasks against comparable implicit and explicit models.

• The paper introduces RevDEQ, which uses an algebraically reversible fixed point solver for exact gradient computation with constant memory.
• It significantly reduces the number of function evaluations, achieving improved performance on language modeling and image classification tasks.
• The approach eliminates the need for extra regularization and is straightforward to implement with modern autodiff frameworks like JAX and PyTorch.

Reversible Deep Equilibrium Models: Exact Gradients and Efficient Implicit Architectures

Introduction

Deep Equilibrium Models (DEQs) define neural network outputs as the fixed point of a learned function, enabling implicit-depth architectures with constant memory complexity. While DEQs have demonstrated strong performance across domains, their training is hampered by the need for approximate gradients via the Implicit Function Theorem (IFT), leading to instability and excessive function evaluations. The paper introduces Reversible Deep Equilibrium Models (RevDEQs), which leverage an algebraically reversible fixed point solver to enable exact gradient computation with constant memory and linear time complexity. This approach eliminates the need for regularization and dramatically reduces the number of function evaluations required for training, resulting in improved performance on large-scale LLMing and image classification tasks.

RevDEQ Architecture and Reversible Fixed Point Solver

RevDEQ extends the standard DEQ formulation by introducing a coupled, reversible fixed point iteration. The forward pass is defined by:

$$\begin{aligned} \mathbf{y}_{n+1} &= (1-\beta)\mathbf{y}_n + \beta f_\theta(\mathbf{z}_n, \mathbf{x}) \ \mathbf{z}_{n+1} &= (1-\beta)\mathbf{z}_n + \beta f_\theta(\mathbf{y}_{n+1}, \mathbf{x}) \end{aligned}$$

where $\mathbf{y}_n, \mathbf{z}_n$ are coupled states, $\beta$ is a relaxation parameter, and $f_\theta$ is the equilibrium function. The backward pass inverts these updates algebraically:

$$\begin{aligned} \mathbf{z}_n &= \frac{\mathbf{z}_{n+1}-\beta f_\theta(\mathbf{y}_{n+1}, \mathbf{x})}{1-\beta} \ \mathbf{y}_n &= \frac{\mathbf{y}_{n+1}-\beta f_\theta(\mathbf{z}_n, \mathbf{x})}{1-\beta} \end{aligned}$$

This reversibility enables exact reconstruction of the forward computation graph during backpropagation, allowing for exact gradients without storing intermediate activations.

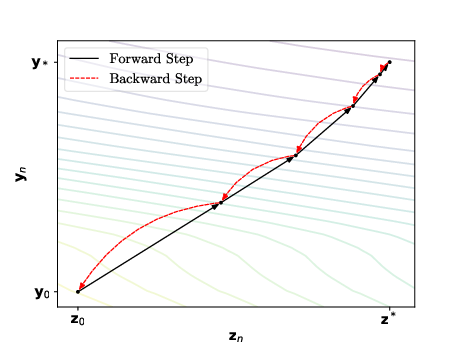
Figure 1: Example of the forward and backward passes in RevDEQ, illustrating the reversible fixed point iteration and exact gradient computation.

The convergence of the reversible scheme is linear in the number of steps, with the same rate as relaxed fixed point iteration. Theoretical analysis shows that both $\mathbf{y}_n$ and $\mathbf{z}_n$ converge to the unique fixed point of $f_\theta$ under contractivity conditions.

Exact Gradient Backpropagation

RevDEQ's reversible solver enables exact reverse-mode automatic differentiation with constant memory. The backpropagation algorithm reconstructs the forward states and propagates adjoints using vector-Jacobian products, matching the gradients obtained by storing the full forward graph. The time complexity is $O(N)$ and memory complexity is $O(1)$, where $N$ is the number of solver steps.

The implementation is straightforward in modern autodiff frameworks (e.g., JAX, PyTorch) by defining custom forward and backward passes for the reversible solver. Mixed precision arithmetic is recommended for addition/subtraction steps to mitigate floating-point error amplification during reversal.

Empirical Results

LLMing: Wikitext-103

RevDEQ is instantiated as a decoder-only transformer, replacing explicit layers with a single equilibrium module. On Wikitext-103, RevDEQ achieves lower perplexity than both DEQ and explicit Transformer-XL models of comparable size, with only 8 function evaluations versus 30 for DEQ. Notably, RevDEQ with 169M parameters achieves a test perplexity of 20.7, outperforming DEQ-Transformer (24.2) and Transformer-XL (24.3).

Scaling experiments show that RevDEQ matches DEQ performance with only 2 function evaluations and plateaus after 8–10 evaluations, indicating superior compute efficiency.

Image Classification: CIFAR-10

RevDEQ is applied to both single-scale and multi-scale architectures, replacing deep unrolled convolutional blocks with a single RevDEQ block per scale. In single-scale settings, RevDEQ achieves 87.5% accuracy with 170K parameters and 8 function evaluations, outperforming DEQ and monDEQ. In multi-scale settings, RevDEQ (5M parameters, 5 evaluations) matches or exceeds the accuracy of explicit ResNet-18 (10M parameters) and ResNet-101 (40M parameters), as well as MDEQ and pcDEQ, while using significantly fewer function evaluations.

(Figure 2)

Figure 2: A single scale of the multi-scale implicit ResNet architecture, illustrating the integration of RevDEQ blocks and downsampling.

Implementation Considerations

• Mixed Precision: Use 64-bit precision for addition/subtraction in the reversible solver to minimize numerical error; other operations can use 32-bit or lower.
• Choice of $\beta$: Lower $\beta$ improves gradient accuracy but slows convergence; values in $[0.5, 0.9]$ are empirically effective.
• Normalisation: Stateless layer-wise normalization is preferred inside $f_\theta$ due to implicit depth; batch normalization is used in explicit downsampling blocks.
• GPU Efficiency: RevDEQ's constant memory backpropagation can be exploited for improved GPU throughput by reducing memory read/write operations.

Limitations and Future Directions

While RevDEQ reduces function evaluations and improves stability, runtime may still exceed explicit models due to solver overhead. Further optimization of GPU kernels and solver implementations is warranted. The approach is readily extensible to other domains where implicit architectures are beneficial, including graph neural networks, generative flows, diffusion models, and inverse problems.

The theoretical framework for reversible solvers may inspire new implicit architectures with exact gradients and efficient memory usage. Future work should explore stateful normalization strategies compatible with implicit depth and investigate applications in large-scale vision and LLMs.

Conclusion

Reversible Deep Equilibrium Models provide a principled solution to the gradient approximation and instability issues of DEQs by introducing an algebraically reversible fixed point solver. This enables exact gradient computation with constant memory, significantly reduces function evaluations, and achieves state-of-the-art results on LLMing and image classification tasks. RevDEQ offers a modular, efficient alternative to explicit deep architectures and sets a new standard for implicit neural models.