Understanding Outer Optimizers in Local SGD: Learning Rates, Momentum, and Acceleration (2509.10439v1)

Abstract: Modern machine learning often requires training with large batch size, distributed data, and massively parallel compute hardware (like mobile and other edge devices or distributed data centers). Communication becomes a major bottleneck in such settings but methods like Local Stochastic Gradient Descent (Local SGD) show great promise in reducing this additional communication overhead. Local SGD consists of three parts: a local optimization process, an aggregation mechanism, and an outer optimizer that uses the aggregated updates from the nodes to produce a new model. While there exists an extensive literature on understanding the impact of hyperparameters in the local optimization process, the choice of outer optimizer and its hyperparameters is less clear. We study the role of the outer optimizer in Local SGD, and prove new convergence guarantees for the algorithm. In particular, we show that tuning the outer learning rate allows us to (a) trade off between optimization error and stochastic gradient noise variance, and (b) make up for ill-tuning of the inner learning rate. Our theory suggests that the outer learning rate should sometimes be set to values greater than $1$. We extend our results to settings where we use momentum in the outer optimizer, and we show a similar role for the momentum-adjusted outer learning rate. We also study acceleration in the outer optimizer and show that it improves the convergence rate as a function of the number of communication rounds, improving upon the convergence rate of prior algorithms that apply acceleration locally. Finally, we also introduce a novel data-dependent analysis of Local SGD that yields further insights on outer learning rate tuning. We conduct comprehensive experiments with standard LLMs and various outer optimizers to validate our theory.

• The paper reveals that tuning the outer learning rate interpolates between minibatch and vanilla Local SGD for optimal convergence.
• It demonstrates that momentum and Nesterov acceleration in the outer loop allow larger effective rates, improving stability and scalability.
• Empirical results on language model pretraining validate that adaptive hyperparameter tuning boosts distributed optimization performance.

Analysis of Outer Optimizers in Local SGD: Learning Rates, Momentum, and Acceleration

Overview

This paper provides a comprehensive theoretical and empirical investigation into the role of the outer optimizer in Local SGD, focusing on the effects of learning rate, momentum, and acceleration in distributed and federated optimization. The authors derive new convergence guarantees, characterize optimal hyperparameter regimes, and validate their findings with large-scale LLM pretraining experiments. The work addresses a critical gap in the understanding of bilevel optimization structures in Local SGD, especially in homogeneous (i.i.d.) data settings, and provides actionable insights for practitioners scaling distributed training.

Theoretical Contributions

Generalized Local SGD and Outer Learning Rate

The analysis centers on Generalized Local SGD, where the outer optimizer applies a learning rate $\gamma$ to aggregated updates from $M$ clients, each performing $H$ local steps with inner learning rate $\eta$. The main convergence theorem demonstrates that the outer learning rate $\gamma$ serves two distinct purposes:

• Interpolation between regimes: By tuning $\gamma$, one can interpolate between the behavior of minibatch SGD ($\gamma > 1$) and vanilla Local SGD ($\gamma = 1$), achieving the best rate of either depending on the problem parameters.
• Robustness to inner learning rate: A large $\gamma$ can compensate for an ill-tuned inner learning rate $\eta$, provided $\eta$ is not excessively large.

The optimal $(\eta, \gamma)$ pair is characterized by a cubic equation, and the analysis shows that $\gamma < 1$ is generally suboptimal for optimization, except in noise-dominated regimes or when generalization is prioritized.

Momentum and Acceleration

The extension to momentum-based outer optimizers reveals that the effective learning rate becomes $\gamma/(1-\mu)$, where $\mu$ is the momentum parameter. This relaxation allows for larger effective learning rates and improved convergence, aligning with empirical practices in federated learning.

For accelerated outer optimizers (Nesterov), the paper provides the first analysis of using acceleration only in the outer loop. The derived rate is accelerated in the number of communication rounds $R$ but not in the number of local steps $H$, reflecting the structure of the algorithm. Compared to prior work (e.g., FedAC), the drift terms exhibit superior scaling with $R$ and $M$.

Data-Dependent Guarantees

A novel high-probability, data-dependent convergence bound is presented, enabling adaptive tuning of $\gamma$ based on observed gradient norms and variance. This result is particularly relevant for practical hyperparameter selection and for understanding the trade-offs in noise-dominated versus optimization-dominated regimes.

Empirical Validation

Convex Quadratic Experiments

Experiments on synthetic quadratic objectives confirm the theoretical predictions: as the noise level $\sigma$ increases, the optimal outer learning rate $\gamma$ decreases, transitioning from optimization-dominated to noise-dominated regimes.

Large-Scale LLM Pretraining

The authors conduct extensive pretraining experiments on Chinchilla-style transformer architectures (150M–1B parameters) using the C4 dataset. Key findings include:

• Outer learning rate selection: For schedule-free SGD, outer learning rates $\gamma > 1$ yield the best perplexity, consistent with theory. Nesterov acceleration also benefits from large effective learning rates.
• Communication frequency: Performance degrades as the number of inner steps $H$ increases (i.e., less frequent synchronization), but schedule-free methods are more robust to this degradation.
• Scaling with replicas: Increasing the number of replicas improves performance up to a plateau, after which flops-efficiency diminishes due to reduced cosine similarity between outer gradients (Figure 1).

  Figure 2: Varying the communication frequency, i.e. number of inner steps $H$, when pretraining from scratch at 150M parameters.

  

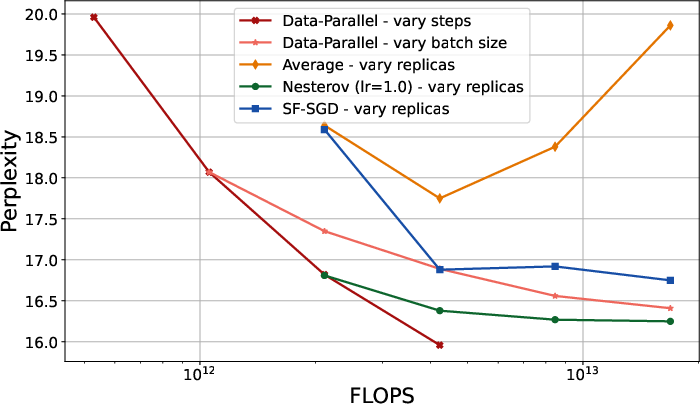
  Figure 3: Pareto front of the flops vs perplexity, comparing various approach scaling the flops budget: increasing the number of steps, increasing the batch size in data-parallel, and increasing the number of replicas for federated learning.

  

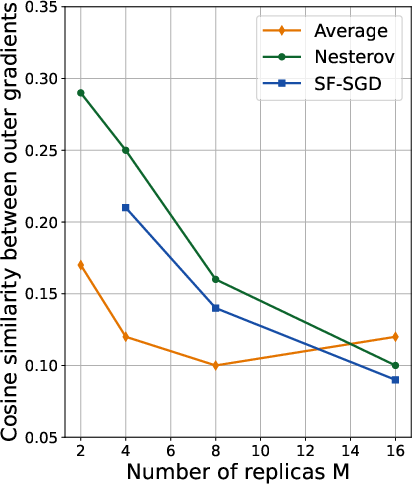
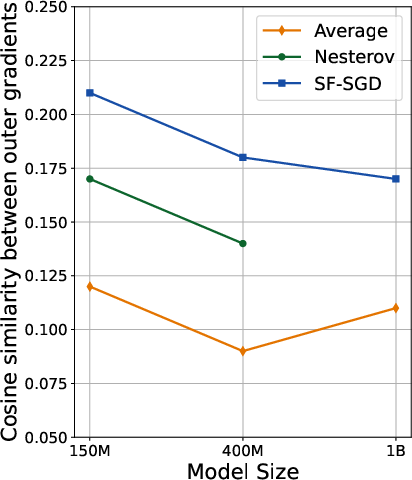
Figure 1: Cosine similarity between outer gradients across different number of replicas (left) and model scales (right). We average the similarity across the middle 50\% of the training.

Figure 4: Tuning b1 decay has a major impact on performance, and its value must be very low.

Implementation and Practical Implications

• Hyperparameter tuning: The explicit characterization of optimal $(\eta, \gamma)$ pairs enables principled tuning in distributed settings. Practitioners should consider $\gamma > 1$ when inner learning rates are conservative or when seeking to match minibatch SGD rates.
• Momentum and acceleration: Momentum in the outer optimizer should be tuned jointly with $\gamma$ to exploit the relaxed stability constraints. Nesterov acceleration in the outer loop is preferable for improved scaling with communication rounds.
• Schedule-free optimization: While schedule-free methods reduce the need for manual learning rate schedules, they still require careful tuning of initial learning rates and decay parameters (e.g., $b_1$ in AdamW).
• Scaling limitations: The diminishing returns in flops-efficiency with increasing replicas highlight a fundamental limitation of federated methods, attributable to reduced gradient alignment. This suggests a need for further research into variance reduction and communication strategies.

Theoretical and Future Directions

The results are derived under the i.i.d. data assumption; extending the analysis to heterogeneous data distributions is a natural next step. The data-dependent bounds and adaptive tuning strategies open avenues for more robust federated optimization in the presence of client failures and communication delays. The observed limitations in scaling with replicas motivate research into new aggregation mechanisms and adaptive communication protocols.

Conclusion

This work advances the theoretical understanding of outer optimizers in Local SGD, providing actionable guidance for distributed training at scale. The dual role of the outer learning rate, the benefits of momentum and acceleration, and the empirical validation on LLMs collectively inform best practices for federated and decentralized optimization. The limitations identified in scaling and hyperparameter sensitivity point to important directions for future research in robust, efficient distributed learning.