Flow Straight and Fast in Hilbert Space: Functional Rectified Flow (2509.10384v1)

Abstract: Many generative models originally developed in finite-dimensional Euclidean space have functional generalizations in infinite-dimensional settings. However, the extension of rectified flow to infinite-dimensional spaces remains unexplored. In this work, we establish a rigorous functional formulation of rectified flow in an infinite-dimensional Hilbert space. Our approach builds upon the superposition principle for continuity equations in an infinite-dimensional space. We further show that this framework extends naturally to functional flow matching and functional probability flow ODEs, interpreting them as nonlinear generalizations of rectified flow. Notably, our extension to functional flow matching removes the restrictive measure-theoretic assumptions in the existing theory of \citet{kerrigan2024functional}. Furthermore, we demonstrate experimentally that our method achieves superior performance compared to existing functional generative models.

• The paper's main contribution is extending rectified flows to infinite-dimensional Hilbert spaces with a marginal-preserving property.
• It introduces a deterministic ODE framework that models functional data effectively and generalizes prior stochastic methods.
• Practical implementations leverage implicit neural representations, transformers, and neural operators, achieving superior results on MNIST, CelebA, and Navier–Stokes data.

Functional Rectified Flow: Extending Rectified Flows to Infinite-Dimensional Hilbert Spaces

Introduction and Motivation

The paper "Flow Straight and Fast in Hilbert Space: Functional Rectified Flow" (FRF) addresses the extension of rectified flow generative models from finite-dimensional Euclidean spaces to infinite-dimensional Hilbert spaces. This generalization is motivated by the need to model inherently functional data—such as time series, solutions to PDEs, and other continuous signals—using generative models that operate directly in function space. Previous work on functional generative modeling, including functional diffusion models and functional flow matching, has been limited by restrictive measure-theoretic assumptions or by reliance on stochastic processes. The FRF framework provides a rigorous, tractable, and marginal-preserving deterministic approach for generative modeling in Hilbert spaces, removing key theoretical barriers and enabling practical implementations across diverse domains.

Theoretical Framework

Rectified Flow in Hilbert Space

The central theoretical contribution is the formulation of rectified flows in general separable Hilbert spaces. Given a stochastic process $X_t$ in $H$, the expected velocity field $v^X(t, x) = \mathbb{E}[\dot{X}_t | X_t = x]$ is defined, and the rectified flow is constructed as the solution to the ODE:

$$Z_t = Z_0 + \int_0^t v^X(s, Z_s) ds, \quad Z_0 \sim X_0$$

where $Z_0$ is sampled from a reference distribution (e.g., Gaussian noise) and $v^X$ is learned to match the velocity of the process interpolating between $X_0$ and $X_1$ (the data distribution).

A key result is the marginal-preserving property: for all $t \in [0,1]$, the distribution of $Z_t$ matches that of $X_t$. This is established via a superposition principle for continuity equations in Hilbert space, leveraging advanced measure-theoretic and functional analytic tools.

Nonlinear Extensions and Connections

The framework naturally generalizes to nonlinear interpolation paths:

$X_t = \alpha_t X_1 + \beta_t X_0$

where $\alpha_t, \beta_t$ are differentiable functions. This subsumes functional flow matching and functional probability flow ODEs as special cases, and removes the restrictive absolute continuity assumptions required in prior work (e.g., [kerrigan2024functional]). The FRF approach is thus strictly more general and applicable.

Implementation Strategies

Approximating the Velocity Field

Directly learning $v^X: H \times [0,1] \to H$ is intractable due to the infinite-dimensional domain. The paper leverages the fact that, for $H = L_2(M)$, functions can be represented by their pointwise evaluations. This enables practical architectures:

• Implicit Neural Representations (INRs): Modulation-based meta-learning, where a shared MLP is adapted per-sample via a modulation vector optimized to fit the discretized function.
• Transformers: Treating discretized function evaluations as sequences with positional encodings, enabling flexible modeling of variable-resolution data.
• Neural Operators: Learning mappings between function spaces using architectures such as the Fourier Neural Operator (FNO), suitable for PDE data and grid-based domains.

Each architecture is adapted to approximate the velocity field on finite discretizations, enabling scalable training and sampling.

Experimental Results

Image Data: MNIST and CelebA

On MNIST ($32 \times 32$), an INR-based FRF model achieves lower FID than functional diffusion processes (FDP), demonstrating improved sample quality with lightweight architectures. Notably, FRF enables super-resolution generation at $64 \times 64$ and $128 \times 128$ from models trained at lower resolution, producing smoother and more coherent samples than naive upscaling.

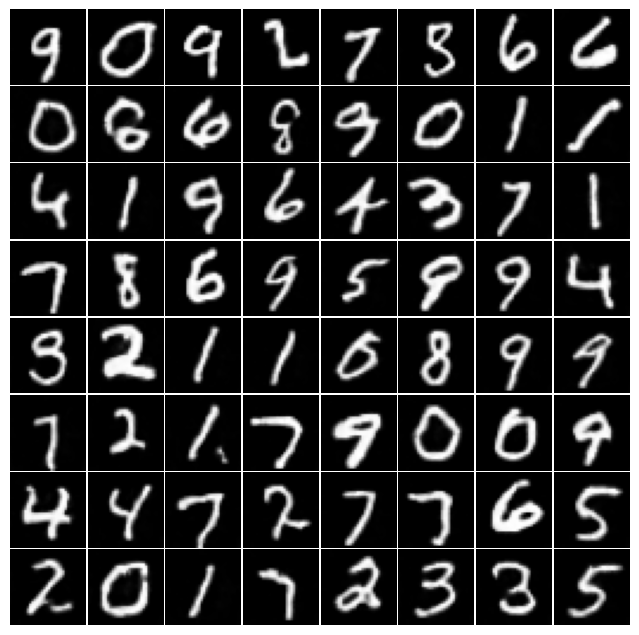
Figure 1: Qualitative results on MNIST: (a) samples generated at the original $32 \times 32$ resolution; (b) super-resolved samples at $64 \times 64$; (c) real MNIST images upscaled to match (b); (d) super-resolved samples at $128 \times 128$; (e) real MNIST images upscaled to match (d).

On CelebA ($64 \times 64$), transformer-based FRF models outperform FDP, FD2F, and $\infty$-DIFF in both FID and FID-CLIP metrics, while being more parameter-efficient than $\infty$-DIFF. Generated samples exhibit high visual fidelity and diversity.

Figure 2: Qualitative results of functional rectified flow with vision transformer.

Additional CelebA samples further demonstrate the consistency and diversity of FRF-generated images.

Figure 3: Additional CelebA samples generated by FRF.

Figure 4: Additional CelebA samples generated by FRF.

Figure 5: Additional CelebA samples generated by FRF.

Figure 6: Additional CelebA samples generated by FRF.

Figure 7: Additional CelebA samples generated by FRF.

PDE Data: Navier-Stokes

On the Navier-Stokes dataset, FRF with a neural operator backbone achieves the lowest density MSE compared to DDO, GANO, functional DDPM, and FFM, indicating superior matching of the spatial distribution of real samples. This demonstrates the effectiveness of FRF for modeling complex functional data in scientific domains.

Properties and Implications

Transport Cost and Straightening Effect

The paper generalizes the convex transport cost reduction and straightening effect of rectified flows to Hilbert spaces. The rectified coupling does not increase transport cost for any convex function, and repeated application of rectified flow progressively straightens the coupling, reducing path overlap and enabling efficient single-step sampling.

Practical and Theoretical Impact

The FRF framework provides a unified, tractable, and theoretically sound foundation for functional generative modeling. It enables efficient deterministic sampling, supports variable resolution, and is compatible with diverse architectures. The removal of restrictive measure-theoretic assumptions broadens applicability to real-world functional data, including scientific simulations, time series, and high-resolution images.

Limitations and Future Directions

While the framework is general, optimal performance in high-complexity domains may require domain-specific architectures and inductive biases. Further research is needed on interpretability, robustness, and safety, especially for applications in synthetic media generation. Theoretical extensions to other classes of function spaces (e.g., Sobolev, Besov) and integration with probabilistic programming are promising directions.

Conclusion

Functional Rectified Flow extends rectified flow generative modeling to infinite-dimensional Hilbert spaces, providing a rigorous, marginal-preserving, and computationally efficient approach for functional data. The framework unifies and generalizes prior functional generative models, achieves strong empirical results across image and scientific domains, and opens new avenues for principled generative modeling in function space.