kNNSampler: Stochastic Imputations for Recovering Missing Value Distributions (2509.08366v1)

Abstract: We study a missing-value imputation method, termed kNNSampler, that imputes a given unit's missing response by randomly sampling from the observed responses of the $k$ most similar units to the given unit in terms of the observed covariates. This method can sample unknown missing values from their distributions, quantify the uncertainties of missing values, and be readily used for multiple imputation. Unlike popular kNNImputer, which estimates the conditional mean of a missing response given an observed covariate, kNNSampler is theoretically shown to estimate the conditional distribution of a missing response given an observed covariate. Experiments demonstrate its effectiveness in recovering the distribution of missing values. The code for kNNSampler is made publicly available (https://github.com/SAP/knn-sampler).

• The paper presents kNNSampler, a kNN-based stochastic imputation method that recovers full conditional distributions rather than just mean estimates.
• It leverages empirical distributions from k-nearest neighbors to capture multimodality and heteroscedasticity, validated using energy distance metrics.
• The method supports uncertainty quantification and multiple imputation, offering practical advantages for robust analyses under MAR conditions.

kNNSampler: Stochastic Imputations for Recovering Missing Value Distributions

Introduction and Motivation

The paper introduces kNNSampler, a stochastic imputation method designed to recover the full conditional distribution of missing values, rather than merely estimating their conditional mean. This approach addresses a critical limitation of standard regression-based imputers such as kNNImputer, which tend to underestimate the variability and multimodality of the true missing value distribution, leading to biased downstream analyses, especially for variance, quantiles, and modes. kNNSampler is conceptually simple: for each missing response, it samples randomly from the observed responses of the $k$ nearest neighbors in covariate space, thereby approximating the conditional distribution $P(y|x)$.

Methodology

Problem Setting

Given a dataset with $n$ complete (covariate, response) pairs and $m$ units with observed covariates but missing responses, the goal is to impute the missing responses such that the joint distribution of imputed data matches the true data-generating process under the MAR assumption. The method assumes access to a distance metric on the covariate space and leverages the empirical distribution of responses among the $k$ nearest neighbors.

kNNSampler Algorithm

For each unit with missing response and observed covariate $\tilde{x}$:

1. Identify the $k$ nearest neighbors among the $n$ observed units in covariate space.
2. Construct the empirical distribution $\hat{P}(y|\tilde{x})$ as the uniform distribution over the responses of these $k$ neighbors.
3. Sample a value from this empirical distribution as the imputed response.

This procedure is repeated independently for each missing value. The only hyperparameter is $k$, which is selected via leave-one-out cross-validation (LOOCV) for kNN regression, using efficient algorithms for scalability.

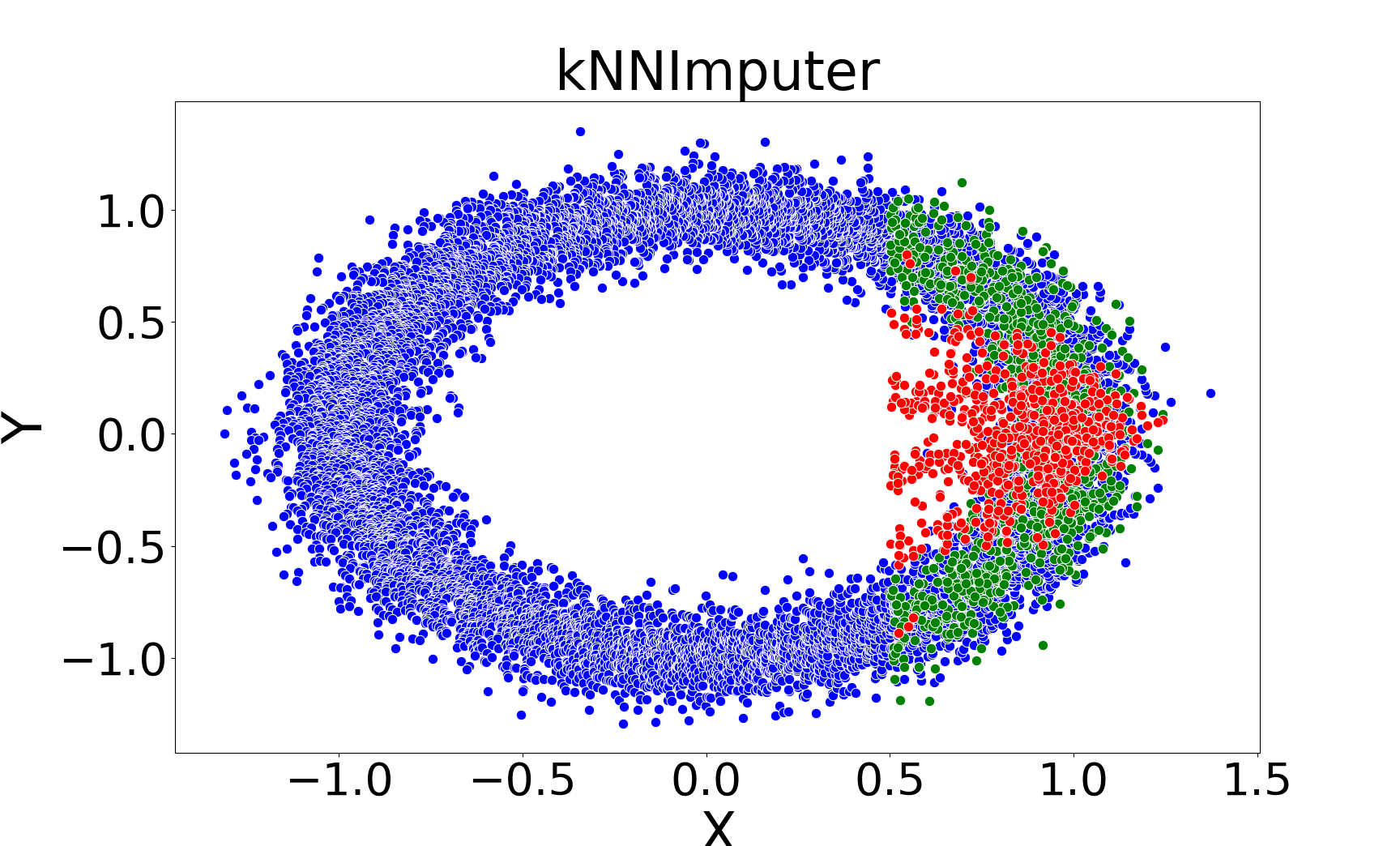
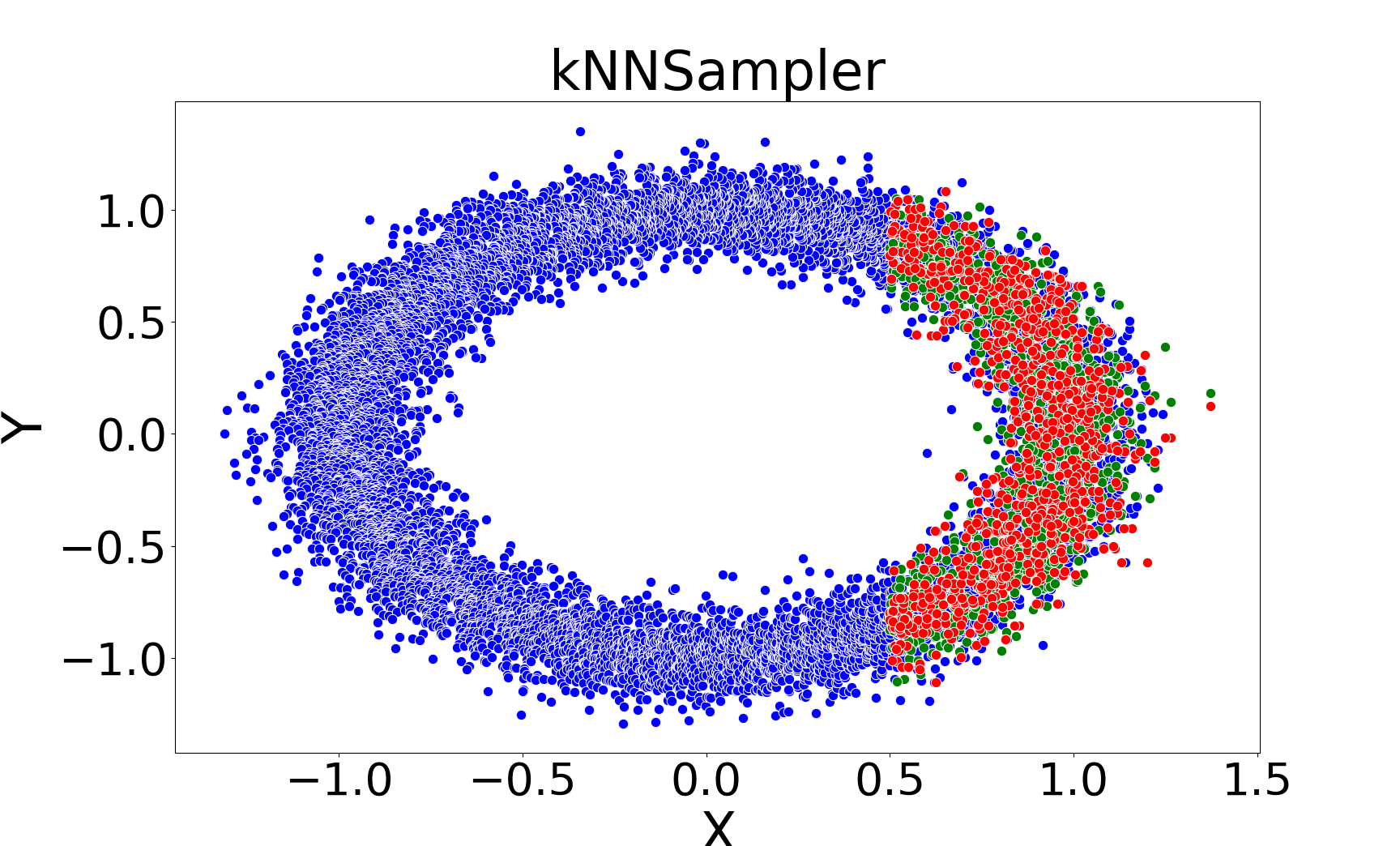
Figure 1: Comparison of imputations by kNNImputer (left) and kNNSampler (right) on a noisy ring dataset, illustrating that kNNSampler better recovers the true distribution of missing values.

Uncertainty Quantification and Multiple Imputation

kNNSampler naturally supports uncertainty quantification:

• Conditional probabilities: Estimated as the fraction of kNN responses falling in a set $S$.
• Prediction intervals: Empirical quantiles of the kNN responses provide valid prediction intervals for missing values.
• Conditional standard deviation: Estimated as the empirical standard deviation of the kNN responses.

Multiple imputation is achieved by generating $B$ independent imputed datasets, each via independent sampling from the kNN empirical distributions, enabling valid inference via Rubin's rules.

Theoretical Analysis

The paper provides a rigorous analysis of the kNNSampler estimator for the conditional distribution $P(y|x)$, leveraging the framework of kernel mean embeddings in RKHS. The main theoretical results are:

• Consistency: Under a Lipschitz condition on the conditional mean embedding and standard regularity assumptions (bounded kernel, finite VC dimension, intrinsic dimension $d$ of the covariate distribution), the kNN empirical conditional distribution converges in MMD to the true conditional distribution as $n \to \infty$, provided $k \to \infty$ and $k/n \to 0$.
• Convergence Rate: The optimal rate is $O(n^{-2/(2+d)})$ (up to log factors), matching the minimax rate for real-valued kNN regression, but extended here to infinite-dimensional RKHS-valued regression.
• Curse of Dimensionality: The convergence rate depends on the intrinsic dimension $d$ of the covariate distribution, not the ambient dimension, mitigating the curse of dimensionality when the data lies on a low-dimensional manifold.
• Support Coverage: The method requires that the support of the covariate distribution for missing units is covered by the observed data; otherwise, imputation is ill-posed.

Empirical Evaluation

Experimental Setup

Two synthetic data models are used:

1. Linear with Chi-square noise: $y = x + \epsilon$, with $\epsilon \sim \chi^2(2)$, to test recovery of asymmetric, non-Gaussian distributions.
2. Noisy 2D ring: $(x, y)$ generated from a noisy ring, yielding multimodal conditional distributions.

Missingness is MAR, with missing responses concentrated in a specific covariate region. Performance is evaluated using the energy distance between the empirical distributions of imputed and true missing values, and permutation test p-values.

Qualitative Results

kNNSampler and kNN$\times$KDE are the only methods that recover the true distribution of missing values, including multimodality and heteroscedasticity. Regression-based methods (linear, Random Forest, kNNImputer) produce imputations concentrated around the conditional mean, underestimating variance and failing to capture distributional features.

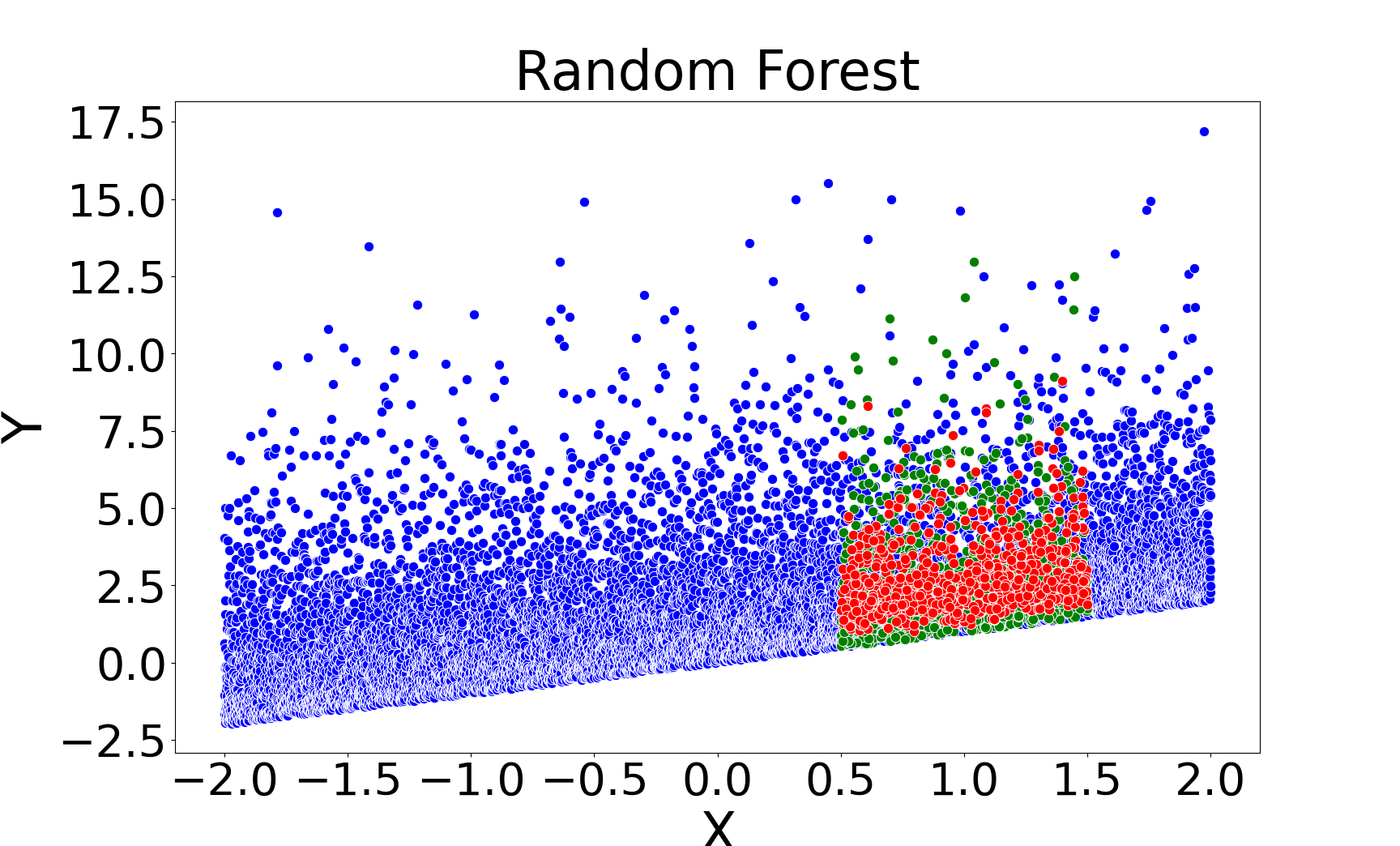
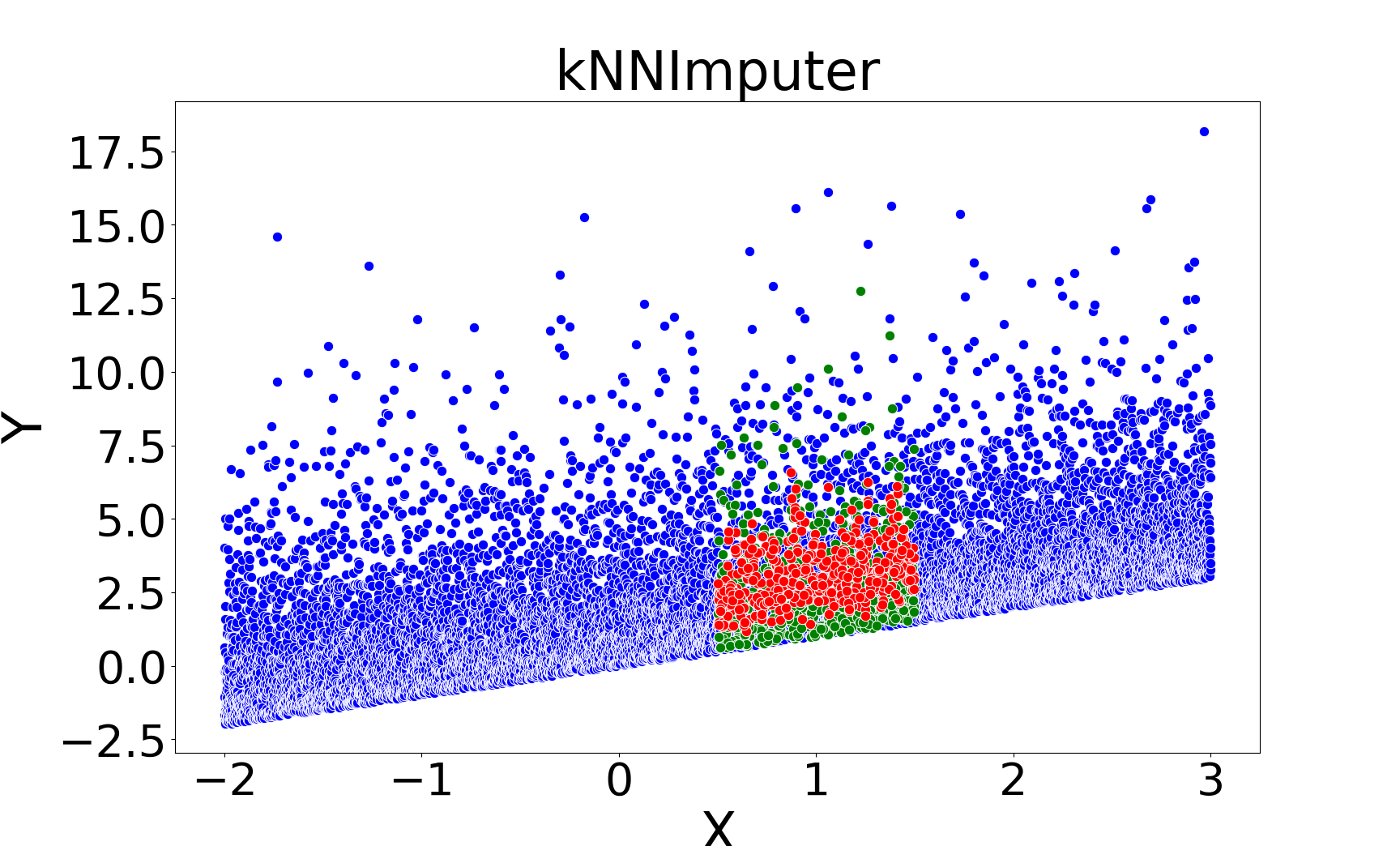
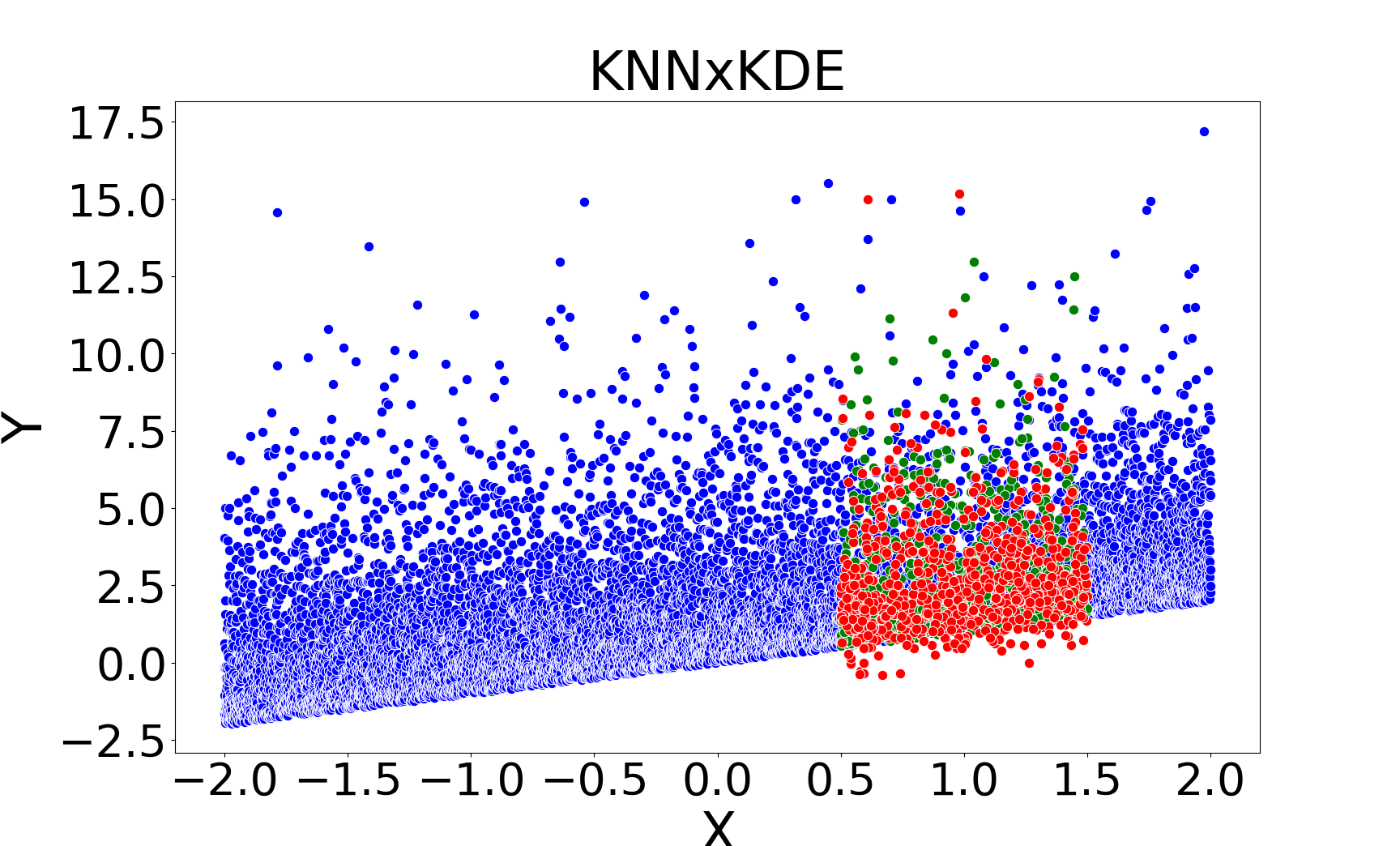
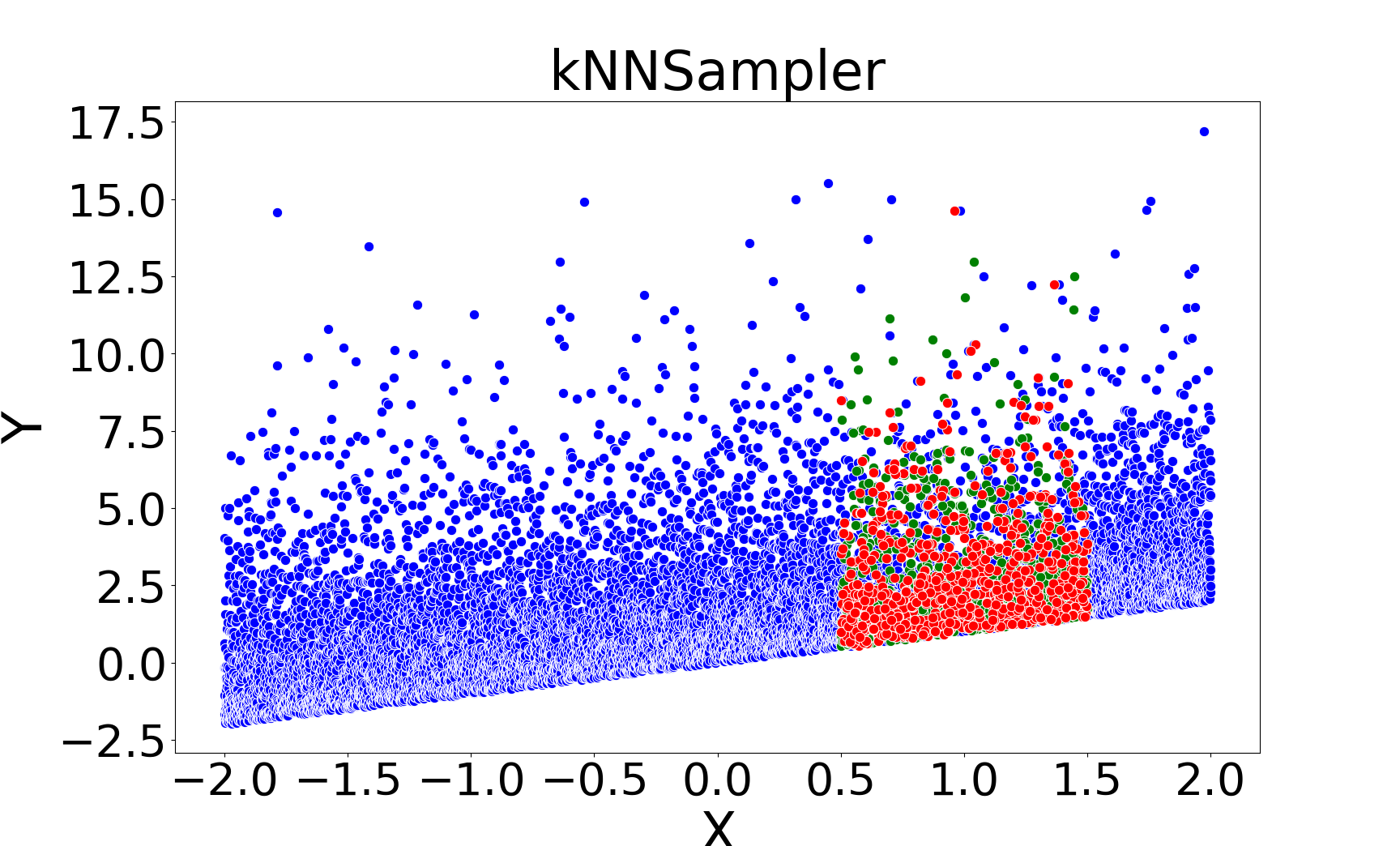
Figure 2: Missing value imputations by different methods for the linear chi-square model, showing that kNNSampler aligns closely with the true missing value distribution.

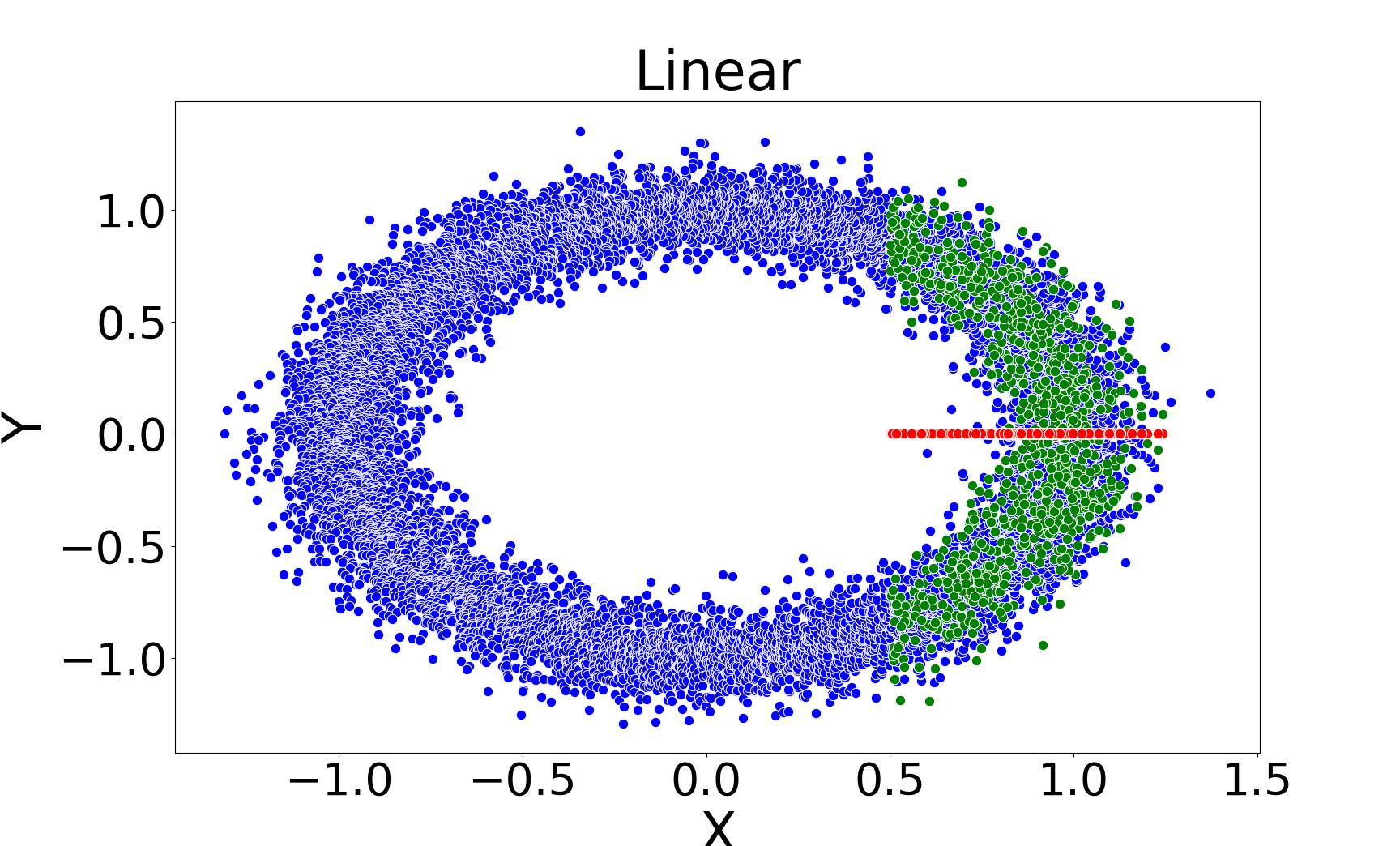
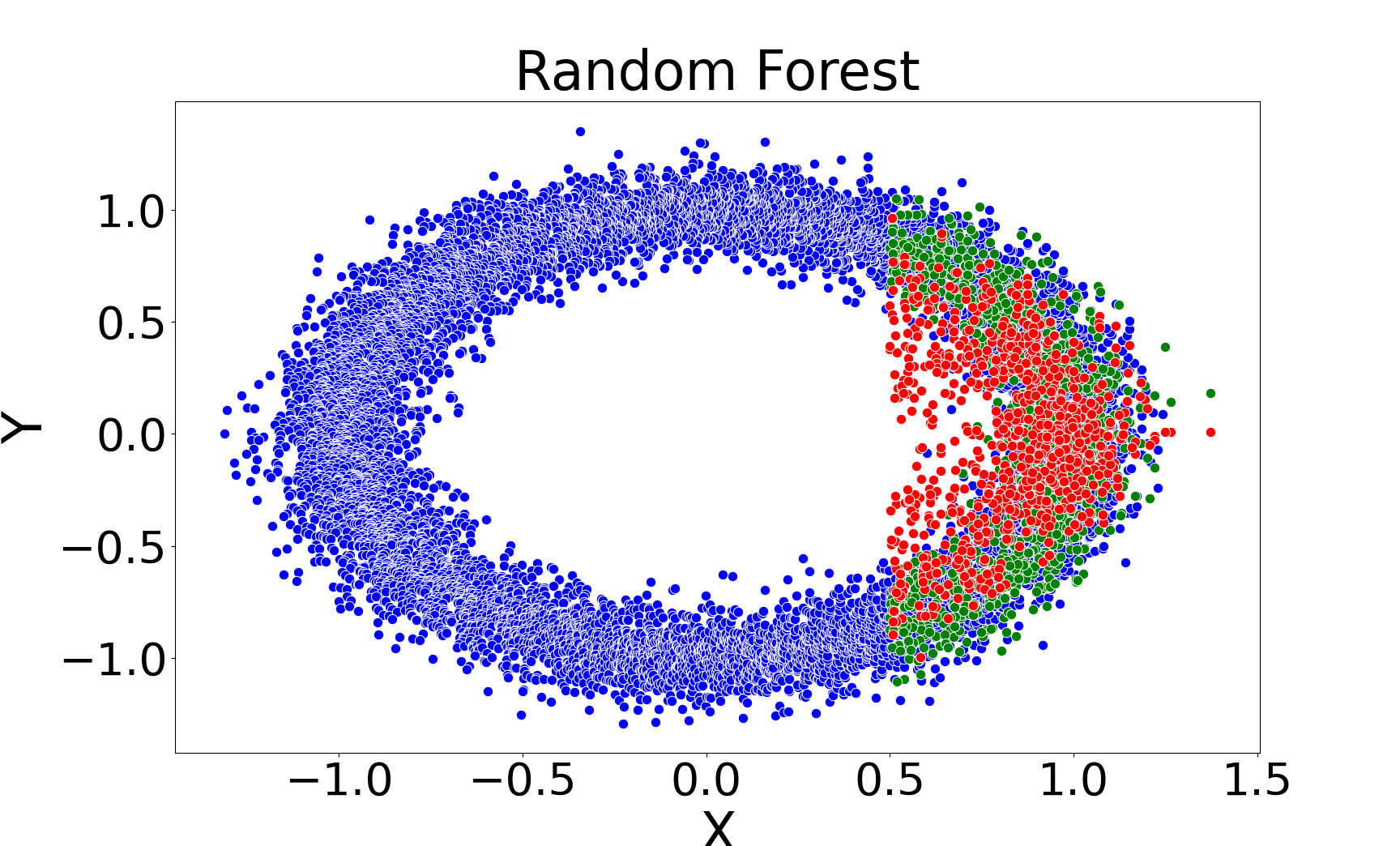
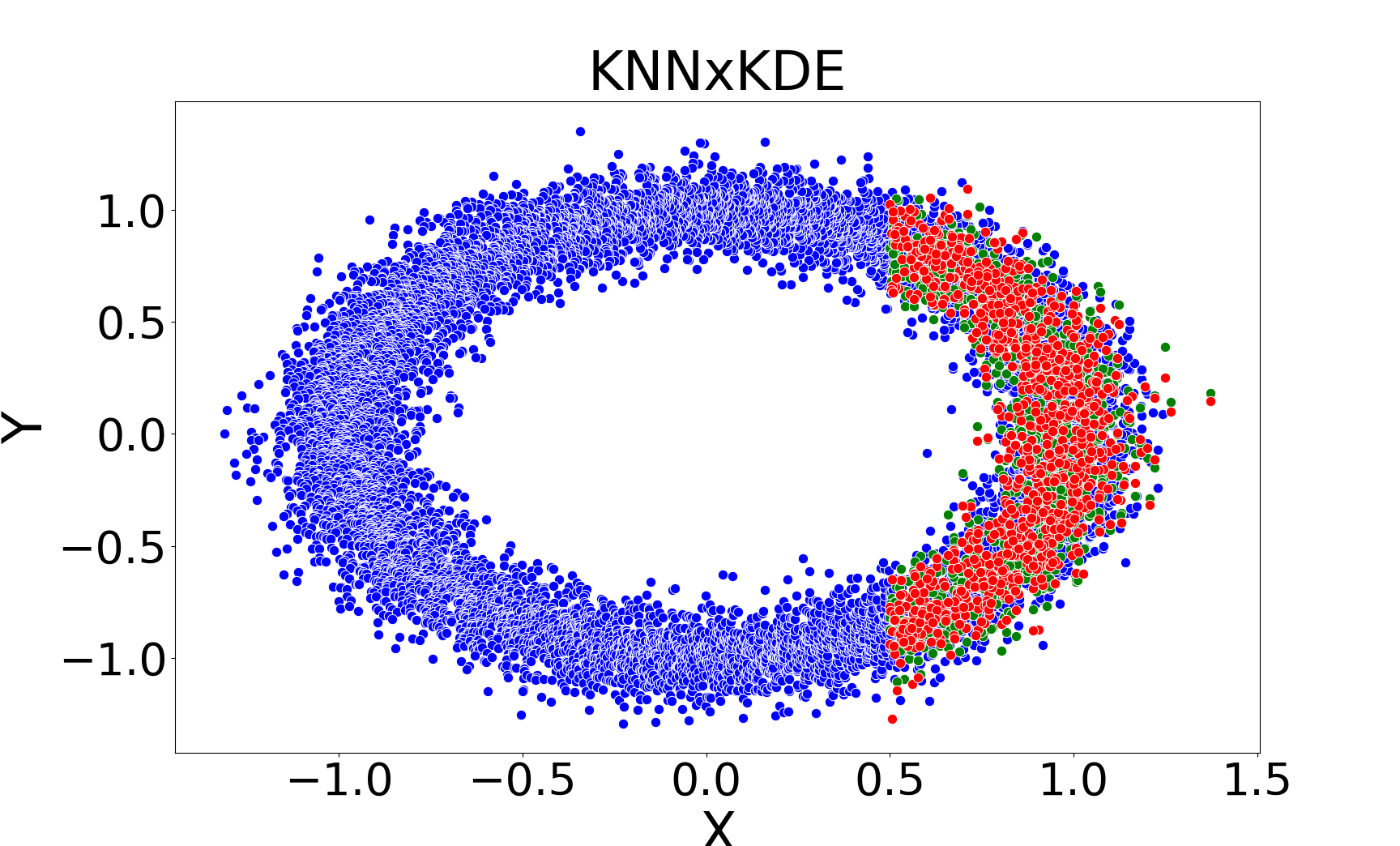
Figure 3: Missing value imputations by different methods for the noisy ring model, highlighting the ability of kNNSampler to recover multimodal distributions.

Quantitative Results

• Energy Distance: kNNSampler achieves the lowest energy distance to the true missing value distribution across all sample sizes and both data models, with low variance across runs.
• Permutation Test p-values: kNNSampler yields high p-values, indicating that the imputed and true distributions are statistically indistinguishable. Competing methods, especially kNN$\times$KDE, show higher variance and occasional significant discrepancies.
• RMSE: Linear imputation achieves the lowest RMSE, but this metric is shown to be misleading for distributional recovery, as it does not capture higher-order moments or multimodality.

  Figure 4: The energy distance between the empirical distributions of imputations and true missing values for the linear chi-square data, demonstrating the superior distributional recovery of kNNSampler.

  

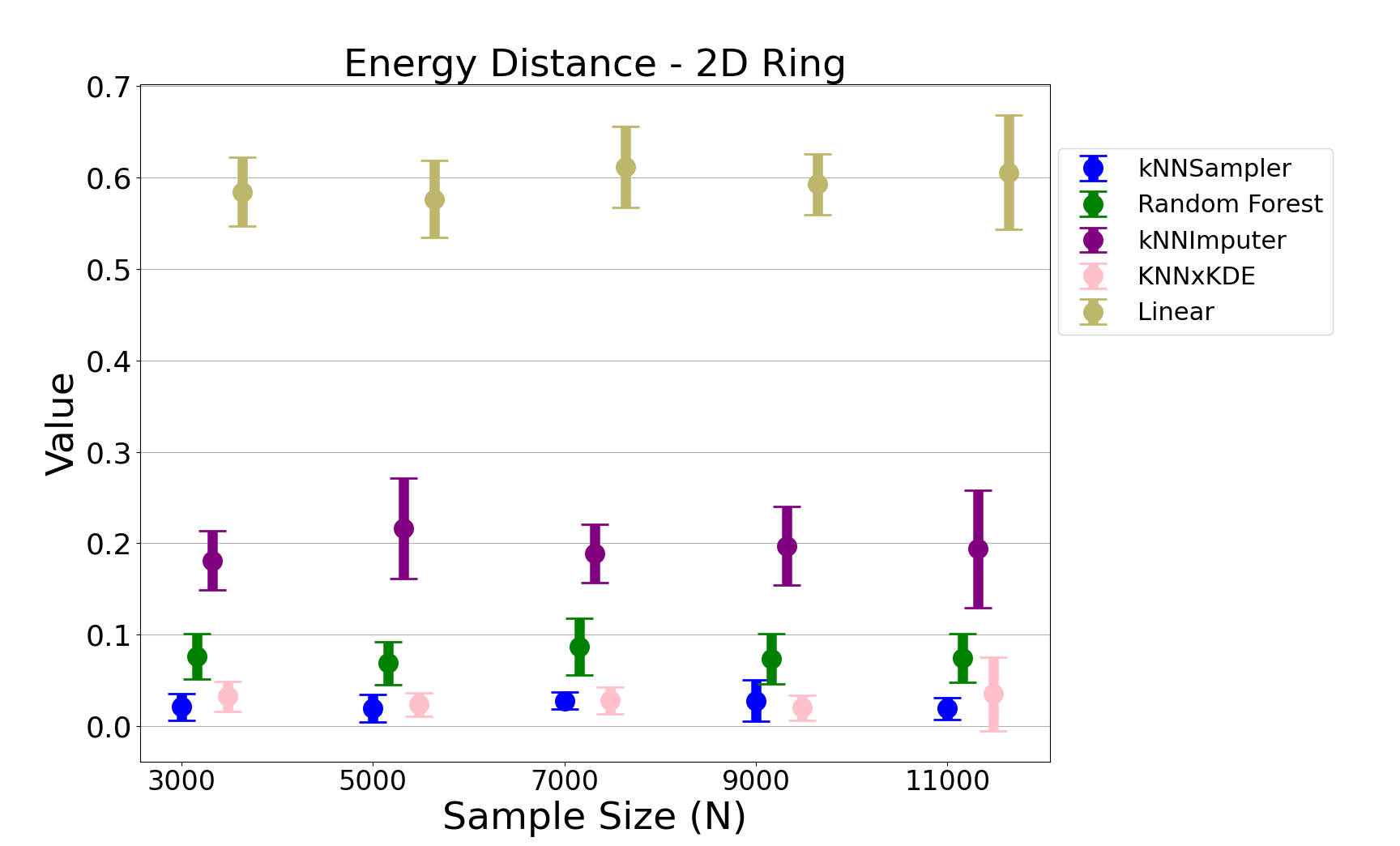
  Figure 5: The energy distance for the noisy ring data, confirming the robustness of kNNSampler across complex distributions.

  

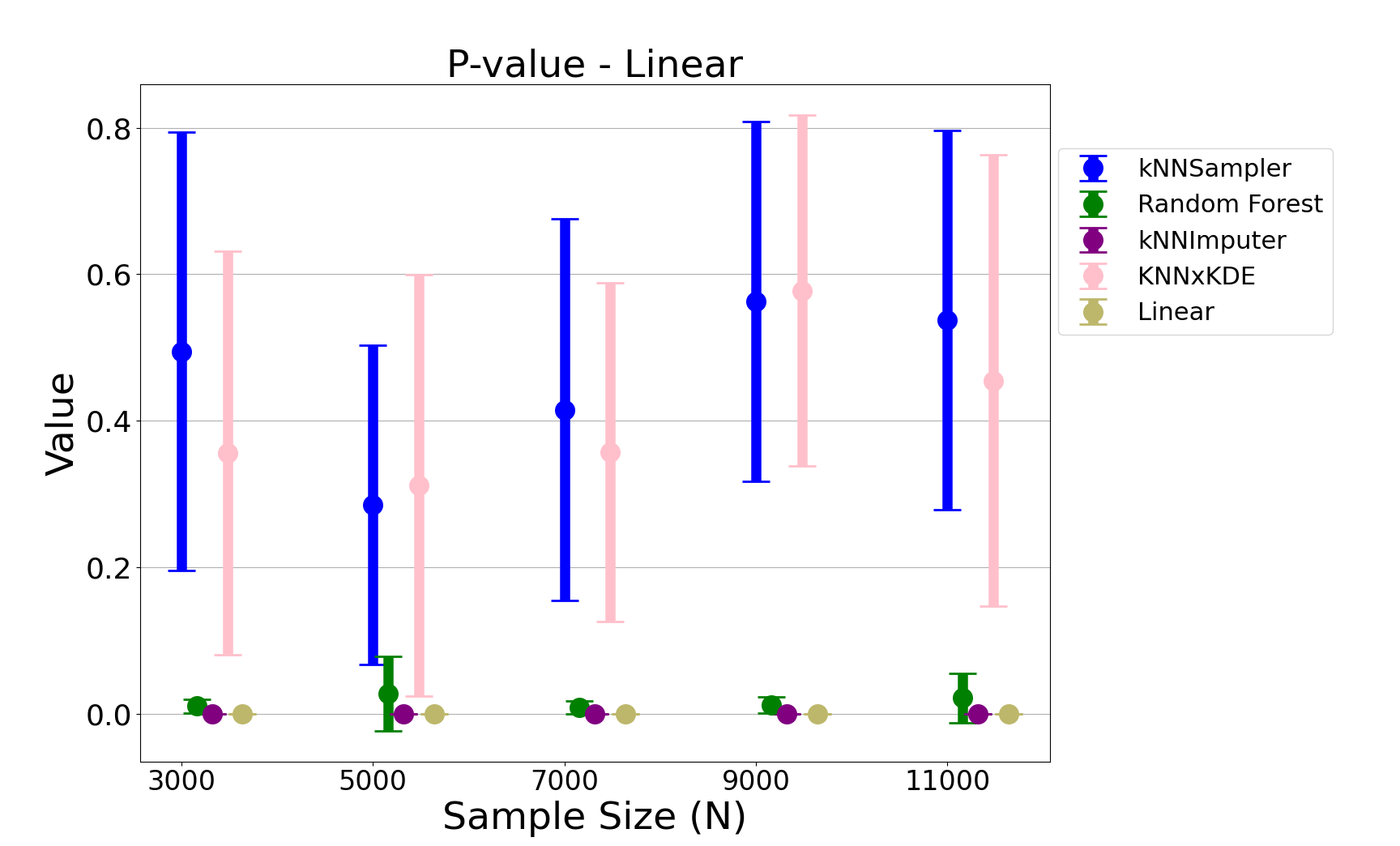
  Figure 6: Permutation test p-values for the linear chi-square data, with kNNSampler consistently yielding high p-values.

  

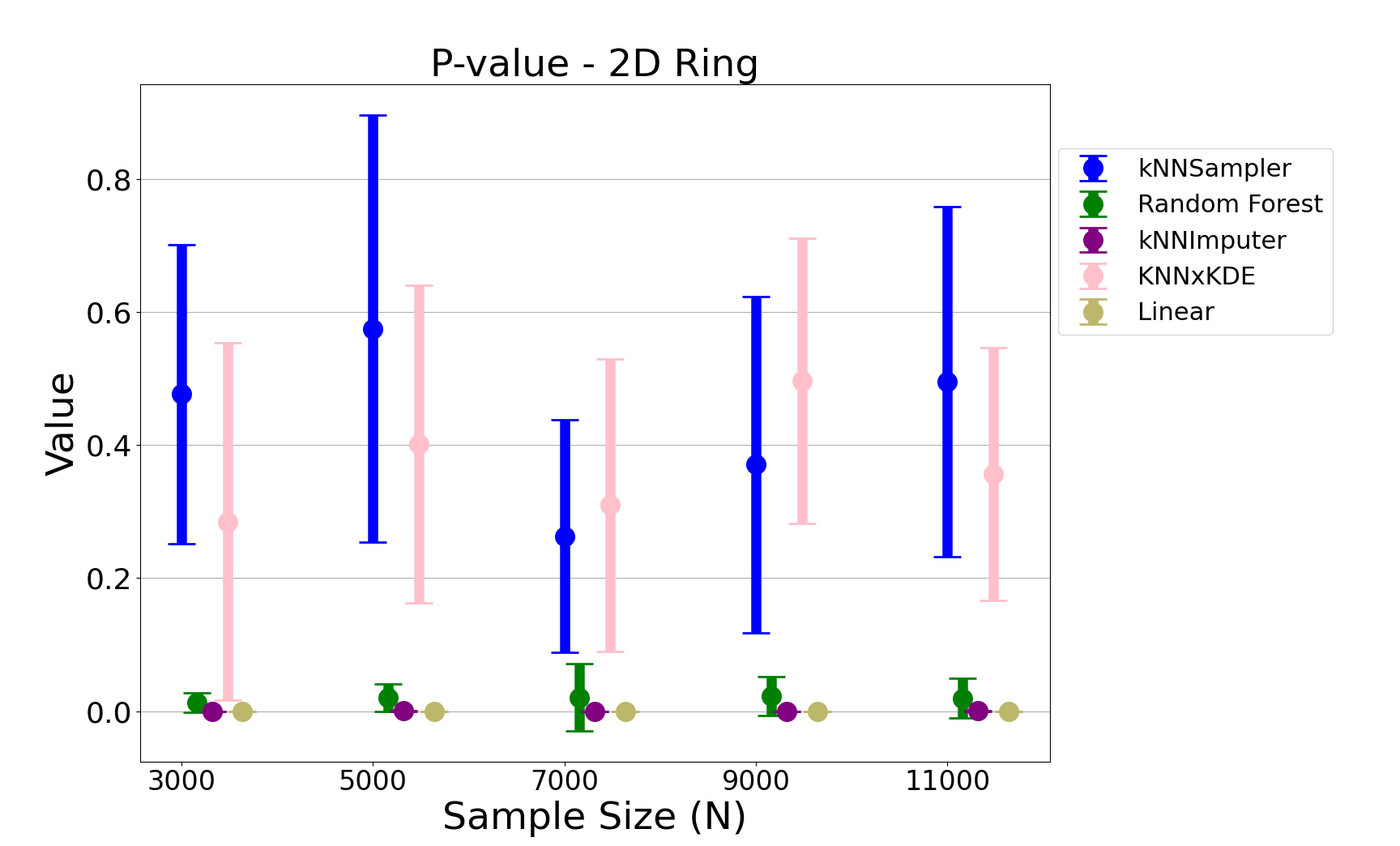
  Figure 7: Permutation test p-values for the noisy ring data, further supporting the statistical indistinguishability of kNNSampler imputations.

Uncertainty Quantification

Empirical coverage of kNN-based prediction intervals matches nominal levels as sample size increases, validating the use of kNNSampler for uncertainty-aware imputation.

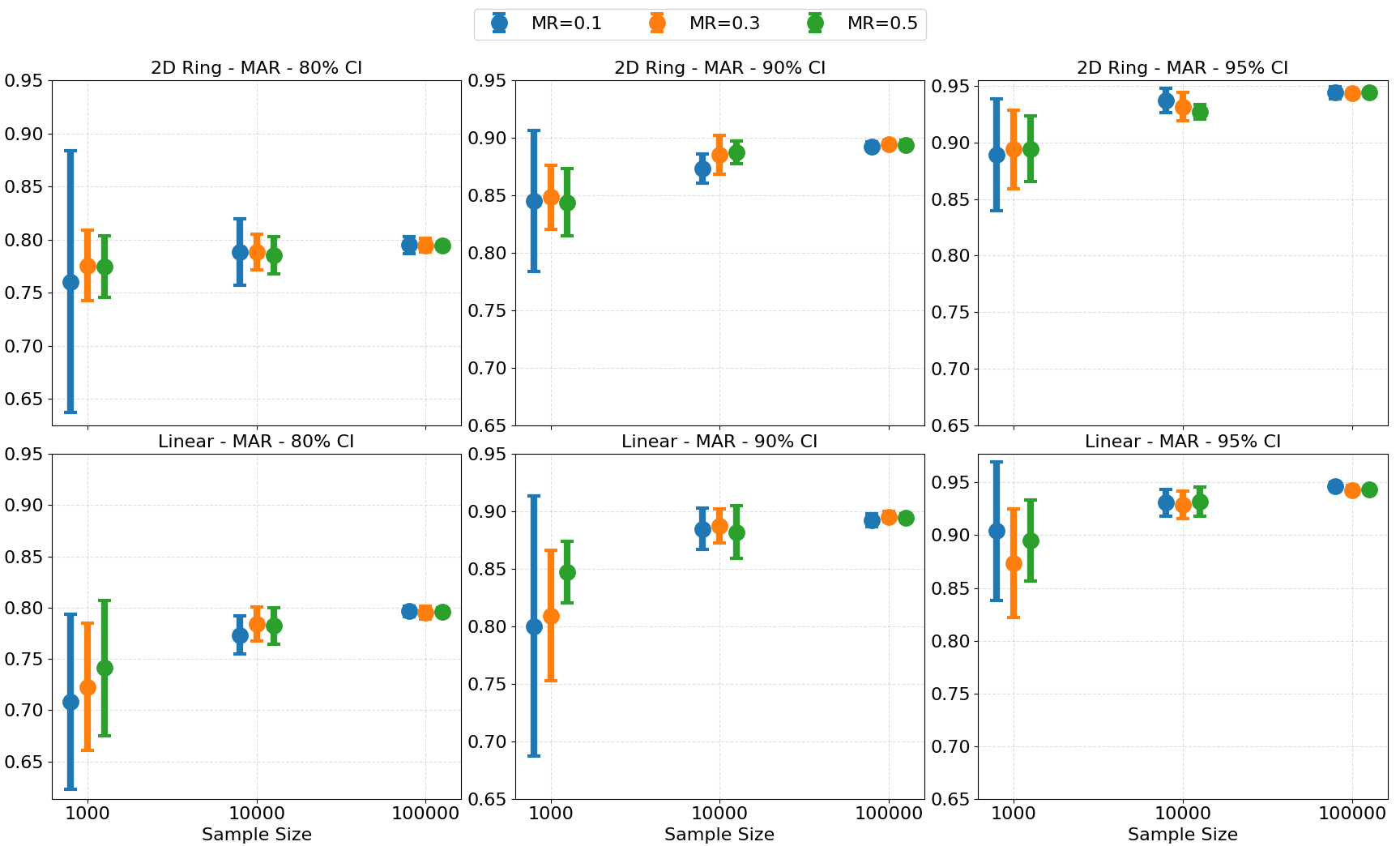
Figure 8: Coverage probabilities of kNN prediction intervals at different missing rates and sample sizes, showing convergence to nominal levels.

Practical Implications and Limitations

kNNSampler is simple to implement, requiring only a nearest neighbor search and random sampling. It is nonparametric, distribution-free, and requires minimal tuning (only $k$). The method is robust to the choice of $k$ when selected via cross-validation and scales well with efficient nearest neighbor algorithms.

However, the method assumes that the observed data adequately covers the covariate space of missing units. In regions of covariate shift or extrapolation, imputation quality degrades. The method is also limited by the computational cost of nearest neighbor search in very high-dimensional or massive datasets, though approximate methods can mitigate this.

Theoretical and Future Directions

The analysis extends the theory of kNN regression to RKHS-valued outputs, providing new insights into the estimation of conditional mean embeddings via nearest neighbor methods. This opens avenues for further research in nonparametric conditional distribution estimation, especially in the context of kernel methods and high-dimensional statistics.

Potential future developments include:

• Extension to categorical or mixed-type data via appropriate distance metrics.
• Integration with deep metric learning for improved neighbor selection in complex feature spaces.
• Adaptation to covariate shift scenarios, leveraging recent advances in nearest neighbor domain adaptation.
• Application to time series and structured data, where temporal or spatial dependencies can be exploited.

Conclusion

kNNSampler provides a theoretically justified, empirically validated, and computationally efficient approach for stochastic imputation of missing values, recovering the full conditional distribution rather than just the mean. It outperforms standard regression-based and density-based imputers in both unimodal and multimodal settings, and supports valid uncertainty quantification and multiple imputation. The method is particularly well-suited for applications where accurate recovery of the distributional properties of missing data is critical for downstream inference and decision-making.