Customizing the Inductive Biases of Softmax Attention using Structured Matrices (2509.07963v1)

Abstract: The core component of attention is the scoring function, which transforms the inputs into low-dimensional queries and keys and takes the dot product of each pair. While the low-dimensional projection improves efficiency, it causes information loss for certain tasks that have intrinsically high-dimensional inputs. Additionally, attention uses the same scoring function for all input pairs, without imposing a distance-dependent compute bias for neighboring tokens in the sequence. In this work, we address these shortcomings by proposing new scoring functions based on computationally efficient structured matrices with high ranks, including Block Tensor-Train (BTT) and Multi-Level Low Rank (MLR) matrices. On in-context regression tasks with high-dimensional inputs, our proposed scoring functions outperform standard attention for any fixed compute budget. On LLMing, a task that exhibits locality patterns, our MLR-based attention method achieves improved scaling laws compared to both standard attention and variants of sliding window attention. Additionally, we show that both BTT and MLR fall under a broader family of efficient structured matrices capable of encoding either full-rank or distance-dependent compute biases, thereby addressing significant shortcomings of standard attention. Finally, we show that MLR attention has promising results for long-range time-series forecasting.

• The paper presents a novel framework that replaces low-rank attention scoring with structured matrices such as BTT and MLR to resolve inherent bottlenecks.
• The approach improves high-dimensional regression, language modeling, and time series forecasting by efficiently encoding distance-dependent compute biases.
• Empirical results demonstrate that structured attention outperforms standard methods while offering significant compute efficiency and memory savings.

Customizing Softmax Attention Inductive Biases via Structured Matrices

Introduction

This paper presents a principled framework for customizing the inductive biases of softmax attention by replacing the standard low-rank scoring function with computationally efficient, high-rank structured matrices. The authors introduce two main classes of structured matrices—Block Tensor-Train (BTT) and Multi-Level Low Rank (MLR)—and demonstrate their utility in resolving the low-rank bottleneck inherent in standard attention, as well as in encoding distance-dependent compute biases. The work further generalizes these constructions under the Multi-Level Block Tensor Contraction (MLBTC) family, providing a unified perspective on efficient, expressive attention mechanisms.

Limitations of Standard Attention

Standard multi-head attention parameterizes the scoring function as a bilinear form with a low-rank matrix, typically $\mathbf{W}_Q \mathbf{W}_K^\top$, where the head dimension $r$ is much smaller than the embedding dimension $D$. This design, while efficient, introduces a low-rank bottleneck that impairs the model's ability to capture high-dimensional relationships, especially in tasks such as in-context regression with high-dimensional inputs. Empirical results show that multi-head attention fails to solve in-context regression unless $r \approx d_{\text{input}}$.

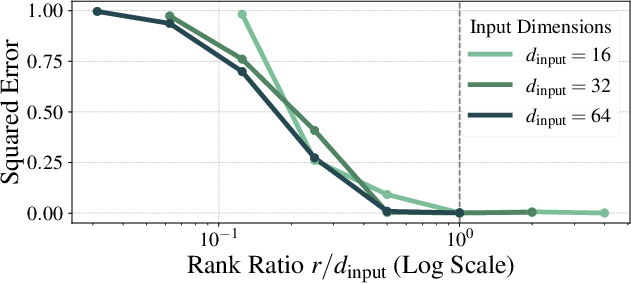
Figure 1: Multi-head attention cannot solve in-context regression unless the head dimension $r$ is close to the input dimension $d_{\text{input}}$.

Additionally, standard attention lacks a distance-dependent compute bias, treating all token pairs equivalently regardless of their relative positions. This is suboptimal for data exhibiting locality, such as natural language or time series, where nearby tokens are more strongly correlated.

Structured Matrix Families for Attention

The authors propose replacing the low-rank scoring function with structured matrices that are both high-rank and computationally efficient. The two main families are:

• Block Tensor-Train (BTT): Capable of expressing full-rank $D \times D$ matrices with $O(D^{3/2})$ parameters and FLOPs, leveraging permutation and block-diagonal structures.
• Multi-Level Low Rank (MLR): Hierarchical summations of low-rank block-diagonal matrices, efficiently capturing both global and local interactions.

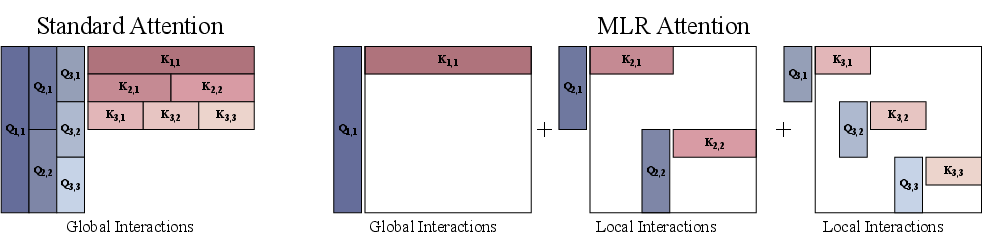
Figure 2: Bilinear forms with structured matrices enable expressive, efficient attention scoring functions.

MLR matrices, in particular, allow for hierarchical allocation of compute, dedicating more resources to local interactions and fewer to distant ones. This enables the encoding of distance-dependent compute biases without resorting to brittle sparsity patterns.

Resolving the Low-Rank Bottleneck

By parameterizing the attention scoring function with BTT or MLR matrices, the model achieves high or full rank without incurring the quadratic cost of dense matrices. Empirical results on in-context regression tasks demonstrate that both Bilinear BTT and Bilinear MLR outperform standard attention for any fixed compute budget, achieving lower regression error with smaller model widths.

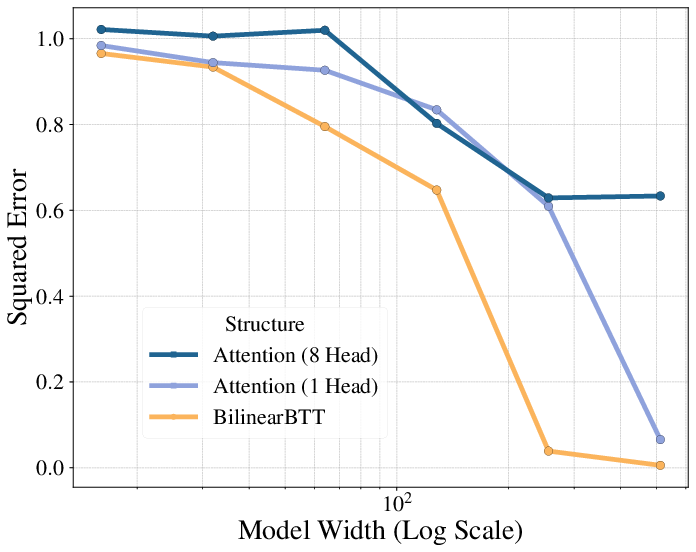
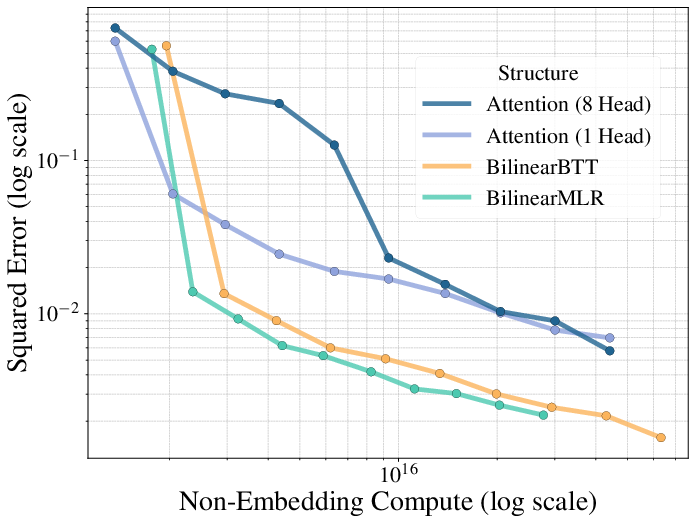
Figure 3: Input dimension ($d_{\text{input}}$) = 128. Bilinear BTT and MLR outperform standard attention for in-context regression.

Encoding Distance-Dependent Compute Bias

MLR attention introduces a flexible, hierarchical distance-dependent compute bias by organizing the score matrix into nested levels. This approach generalizes sliding window attention, allowing for efficient global and local interactions. The number of levels, block sizes, and rank allocations are hyperparameters, enabling fine-grained control over the inductive bias.

MLR attention also reduces key cache size during autoregressive generation, offering practical memory savings. The method is compatible with grouped-query attention and relative positional encoding schemes such as RoPE.

Empirical Results

In-Context Regression

Structured attention variants resolve the low-rank bottleneck, achieving superior performance on high-dimensional regression tasks. Bilinear BTT and MLR attention consistently outperform standard multi-head attention, both in terms of error and compute efficiency.

LLMing

MLR attention achieves improved scaling laws on OpenWebText, outperforming both standard attention and sliding window variants across model widths and compute budgets.

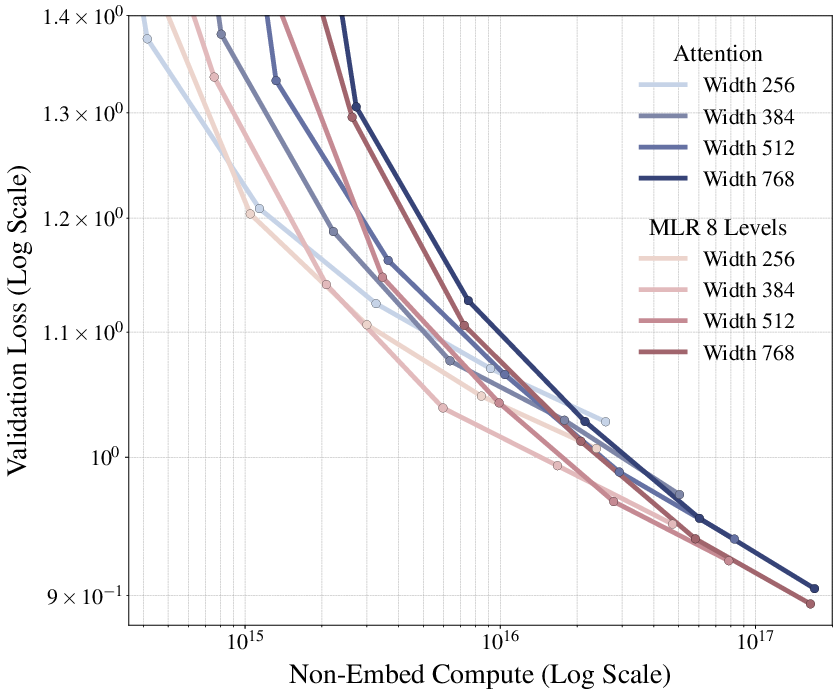
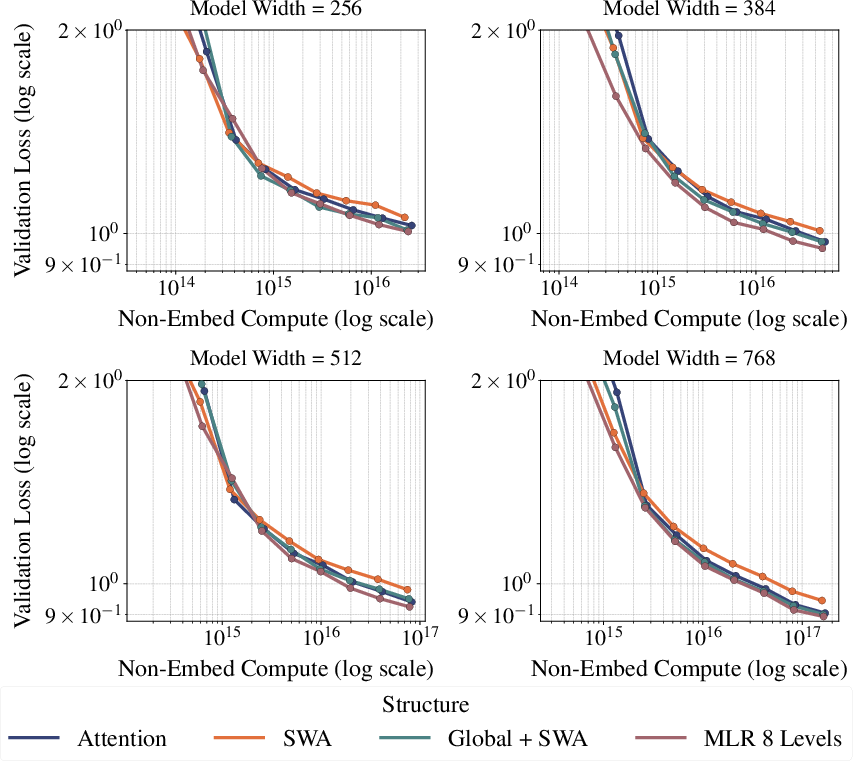
Figure 4: Scaling law on OpenWebText. MLR attention achieves lower validation loss compared to standard attention and SWA variants.

Time Series Forecasting

Substituting standard attention with MLR attention in Chronos and ETT models yields lower validation loss and improved forecasting accuracy, especially as the time horizon increases.

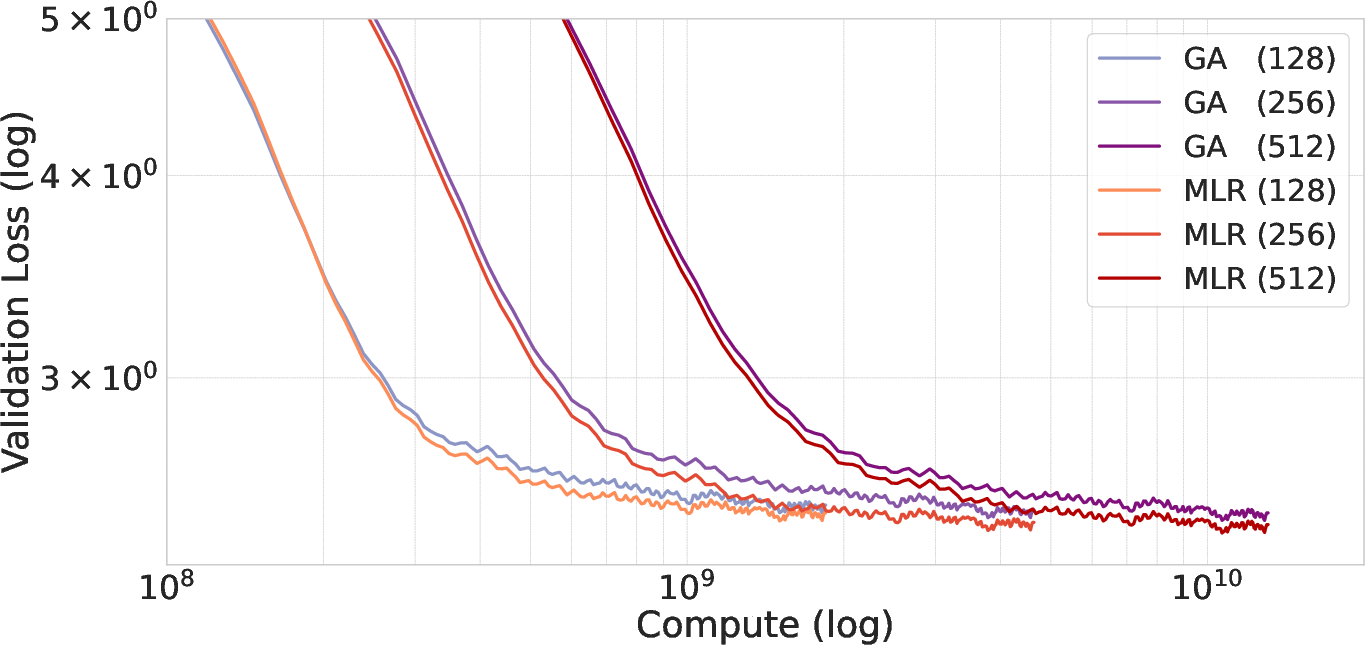
Figure 5: MLR attention reduces computational cost compared to standard attention in Chronos models.

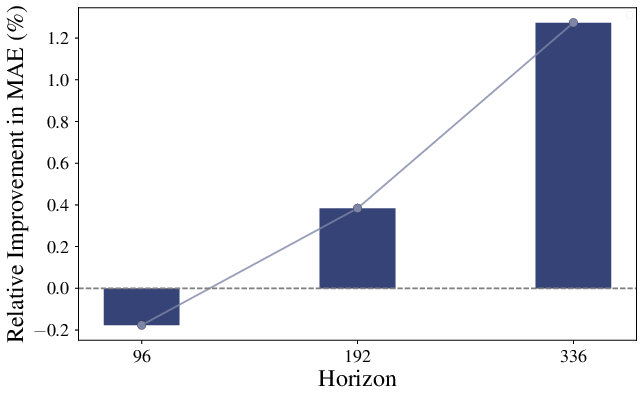
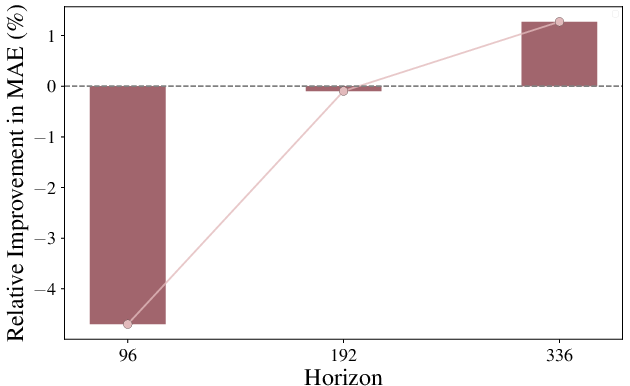
Figure 6: 2-levels MLR attention on ETTh1 shows improved oil temperature prediction accuracy as the time horizon grows.

Generalization: Multi-Level Block Tensor Contraction (MLBTC)

The MLBTC family unifies BTT, MLR, Monarch, Butterfly, Kronecker, and low-rank matrices under a single framework. MLBTC matrices can encode full-rank or distance-dependent compute biases, offering a broad design space for efficient, expressive attention mechanisms.

Implementation Considerations

Efficient implementation is achieved via batched matrix multiplications and optimal tensor contraction order. The authors provide recipes for initialization and learning rate scaling (Maximal Update Parameterization, $\mu$P) to ensure stable feature learning across model widths. The structured attention variants are compatible with standard transformer architectures and can be integrated with existing normalization and positional encoding schemes.

Implications and Future Directions

The proposed framework enables the principled customization of attention inductive biases, addressing key limitations of standard attention. The empirical results suggest that structured attention mechanisms can improve performance and efficiency in tasks with high-dimensional inputs or strong locality patterns. The MLBTC generalization opens avenues for further exploration of structured matrix families in attention and other neural network components.

Potential future directions include:

• Application to scientific and PDE data, point clouds, and code generation tasks with hierarchical structure.
• Fine-tuning and model compression using structured attention.
• Heterogeneous allocation of structured matrices across attention heads for improved division of labor.

Conclusion

This work provides a rigorous framework for customizing the inductive biases of softmax attention via structured matrices, resolving the low-rank bottleneck and enabling efficient, hierarchical distance-dependent compute. The empirical results demonstrate strong improvements in regression, LLMing, and time series forecasting. The generalization to MLBTC matrices offers a unified perspective on efficient, expressive attention mechanisms, with significant implications for the design of future transformer architectures.