Attention as an Adaptive Filter (2509.04154v1)

Abstract: We introduce Adaptive Filter Attention (AFA), a novel attention mechanism that incorporates a learnable dynamics model directly into the computation of attention weights. Rather than comparing queries and keys directly, we model the input sequence as discrete observations of a linear stochastic differential equation (SDE). By imposing a linear dynamics model with simultaneously diagonalizable state matrices and noise covariances, we can make use of a closed-form solution to the differential Lyapunov equation to efficiently propagate pairwise uncertainties through the dynamics. Attention naturally arises as the maximum likelihood solution for this linear SDE, with attention weights corresponding to robust residual-based reweightings of the propagated pairwise precisions. Imposing an additional constraint on the state matrix's eigenvalues leads to a simplified variant with the same computational and memory complexity as standard attention. In the limit of vanishing dynamics and process noise, and using a small-angle approximation, we recover ordinary dot-product attention.

• The paper's main contribution is the formulation of Adaptive Filter Attention (AFA) as a maximum likelihood estimator for linear SDEs, enabling robust filtering of noisy observations.
• It introduces a tensorized attention mechanism that computes weights by propagating uncertainties via closed-form solutions and employing an iteratively reweighted least squares update.
• Experimental results demonstrate that AFA outperforms standard attention by capturing temporal structure and delivering interpretable periodic state estimates.

Attention as an Adaptive Filter: A SDE-Based Framework for Structured Attention

The paper "Attention as an Adaptive Filter" (2509.04154) introduces Adaptive Filter Attention (AFA), a novel attention mechanism that integrates a learnable linear stochastic differential equation (SDE) model directly into the computation of attention weights. This approach unifies the strengths of self-attention and state space models (SSMs) by explicitly modeling temporal structure and uncertainty propagation, yielding a principled, robust, and interpretable alternative to standard dot-product attention. The work provides both a theoretical foundation and practical algorithms for implementing attention as a maximum likelihood estimator (MLE) for linear SDEs, with efficient closed-form solutions under diagonalizability assumptions.

---

Theoretical Framework: Attention as Maximum Likelihood Estimation for SDEs

AFA is motivated by the observation that standard self-attention, while highly parallelizable, lacks the temporal regularization and uncertainty propagation inherent in recursive models like RNNs and Kalman filters. The core insight is to reinterpret the input sequence as noisy, discrete observations of a latent state evolving according to a linear SDE: $$d\mathbf{x}(t) = \mathbf{A} \mathbf{x}(t) dt + \mathbf{B} d\mathbf{w}(t), \quad \mathbf{z}(t_k) = \mathbf{C} \mathbf{x}(t_k) + \mathbf{v}(t_k)$$ where $\mathbf{A}$ is the state matrix, $\mathbf{B}$ the process noise, and $\mathbf{C}$ the measurement matrix.

The attention mechanism is then derived as the MLE for the latent trajectory, with attention weights corresponding to robust, residual-based reweightings of pairwise propagated precisions. The propagation of uncertainty is handled via the closed-form solution to the differential Lyapunov equation, exploiting simultaneous diagonalizability of the system and noise matrices. This yields efficient computation of pairwise covariances and precisions, which are used to adaptively weight the contributions of each observation.

---

Robust Adaptive Filtering and IRLS

AFA generalizes the classical Kalman filter by introducing robust, residual-based reweighting of the propagated precisions. This is formalized via a variational Bayesian treatment, where the precision for each pairwise comparison is adaptively scaled based on the Mahalanobis distance between the predicted and observed states. The resulting update is equivalent to an iteratively reweighted least squares (IRLS) procedure, with the robust weights down-weighting outlier observations.

The IRLS update for the latent state at time $i$ is: $$\mathbf{\hat z}^{(k+1)}_{ii} = \left(\sum_j w_{ij}^{(k)} \mathbf{P}^{C (k)}_{ij}\right)^{-1} \sum_j w_{ij}^{(k)} \mathbf{P}^{C (k)}_{ij} \mathbf{\hat z}_{ij}^{(k)}$$ where $w_{ij}^{(k)}$ is a robust weight based on the residual, and $\mathbf{P}^{C (k)}_{ij}$ is the propagated precision.

This robustification is critical for handling model mismatch and non-Gaussian noise, and provides a principled mechanism for adaptively controlling the influence of each observation.

---

Tensorized and Memory-Efficient Attention Formulations

AFA generalizes the robustified MLE to a tensorized attention mechanism, parameterized by complex-valued query, key, value, and output matrices. The attention computation involves:

• Propagating each key and value through the learned SDE dynamics to the query time via matrix exponentials.
• Computing pairwise residuals and propagated precisions for all query-key pairs.
• Applying robust, residual-based weights to the precisions.
• Aggregating the pulled-forward values via a precision-weighted sum.

To address the quadratic memory bottleneck, the paper introduces several optimizations:

• Convolutional representation: For equally spaced time steps, the matrix exponentials and precisions can be represented as convolutional kernels, reducing memory from $O(m^2 d)$ to $O(md)$.
• Broadcasting and factorization: The pulled-forward estimates and residuals are factorized to avoid explicit construction of large tensors.
• Isotropic and unitary dynamics: Further constraints (e.g., shared real part of eigenvalues, purely imaginary eigenvalues) enable additional simplifications, reducing the computation to a form closely resembling standard attention with complex-valued rotary positional encodings.

---

Implementation Details

AFA is implemented as a neural network layer with the following key components:

• Complex-valued linear layers for queries, keys, values, and output projections, implemented via real-valued block matrices.
• Learnable SDE parameters: decay rate $\alpha$, frequencies $\boldsymbol{\omega}$, process noise $\sigma^2$, measurement noise $\eta^2$.
• Efficient kernel computation for matrix exponentials and precisions.
• Robust weighting via Mahalanobis distance-based softmax or rational forms.
• Residual connections and gating for iterative refinement.

A single-head version is described in detail, with multi-head extensions following the standard Transformer paradigm.

---

Experimental Results

AFA is evaluated on simulated 2D linear systems with varying levels of process and measurement noise. The experiments demonstrate:

• Accurate trajectory filtering: AFA recovers the latent trajectory from noisy measurements, outperforming standard attention in single-layer settings.
• Interpretability: The learned attention matrices exhibit clear periodic structure aligned with the underlying system dynamics, in contrast to the less structured attention of standard Transformers.

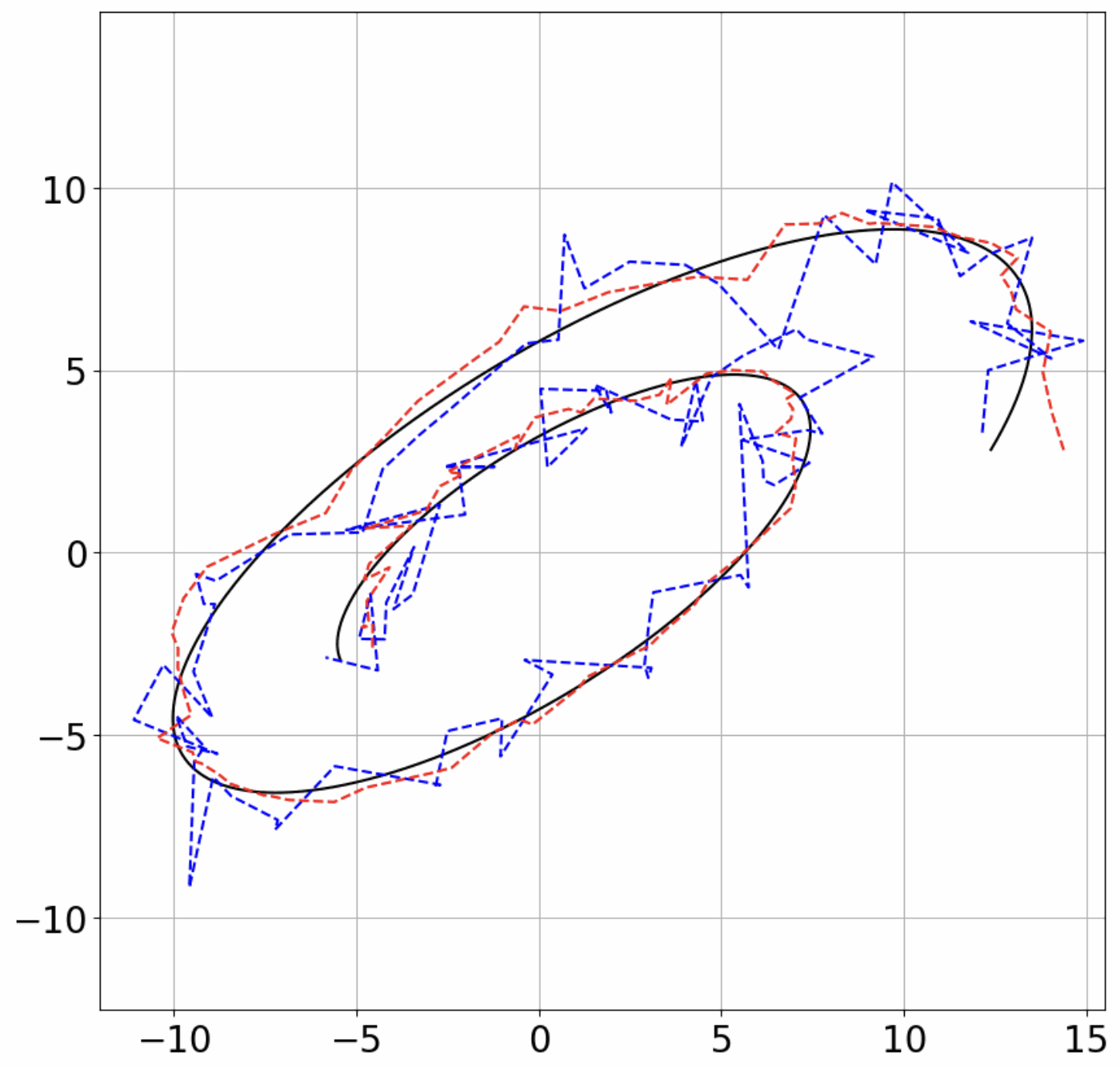
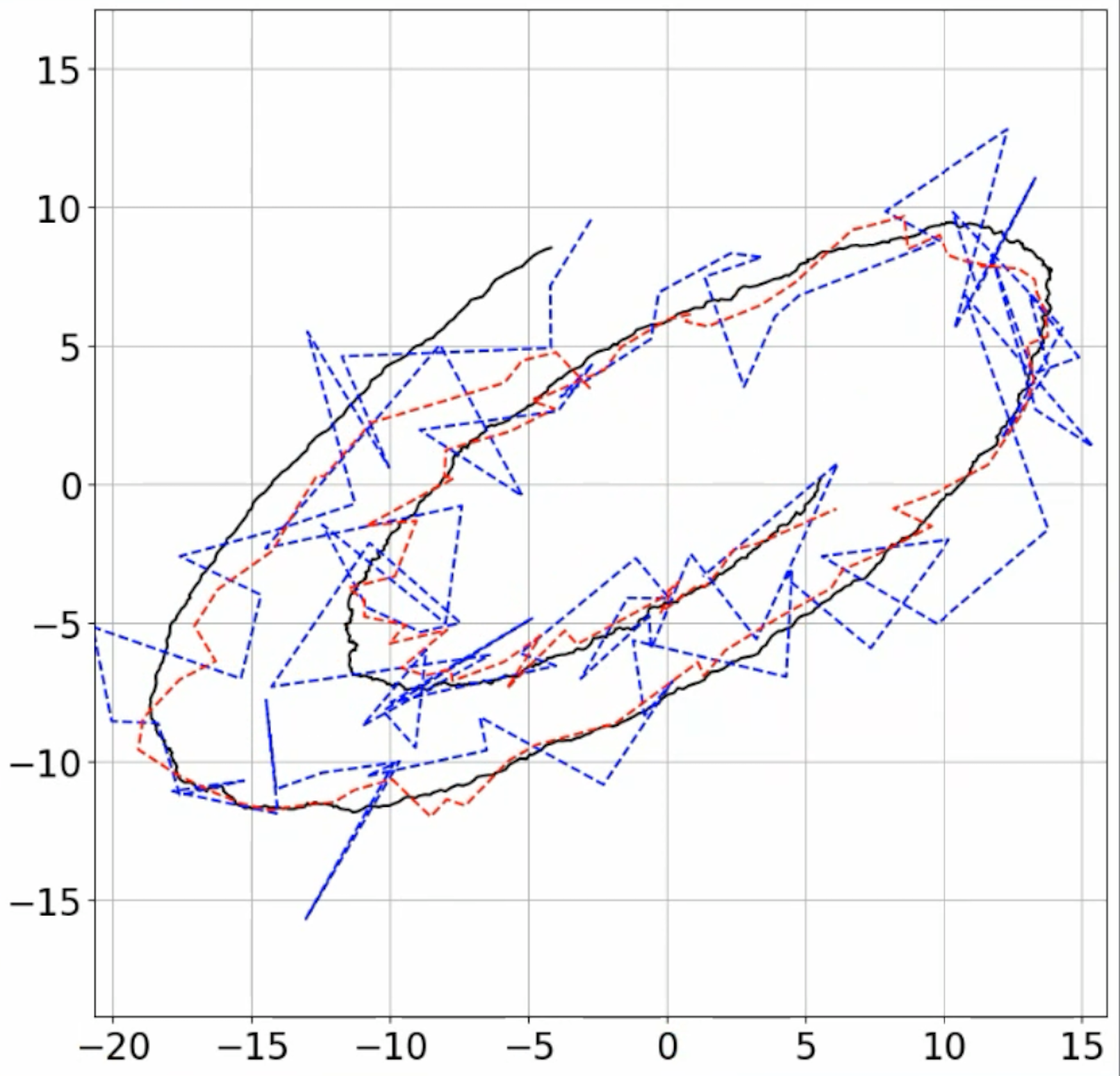
Figure 1: Filter performance on different 2D systems: ground-truth trajectory (black), measured (blue), and predicted (red) for varying noise levels.

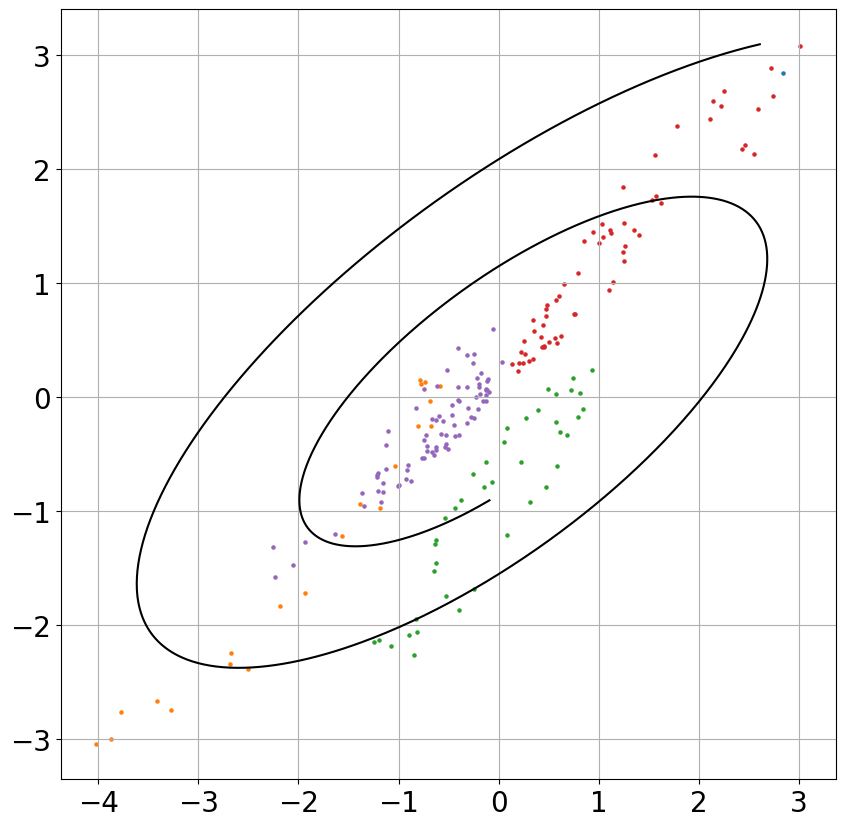
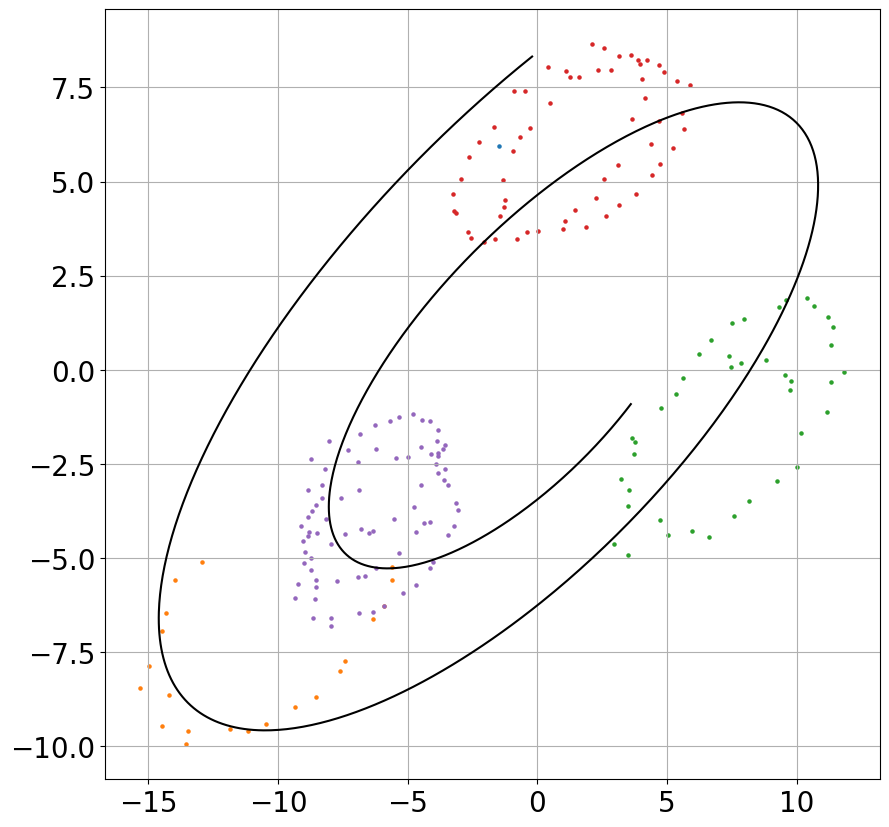
Figure 2: Evolution of "pulled-forward" state estimates during training, converging to the ground truth trajectory.

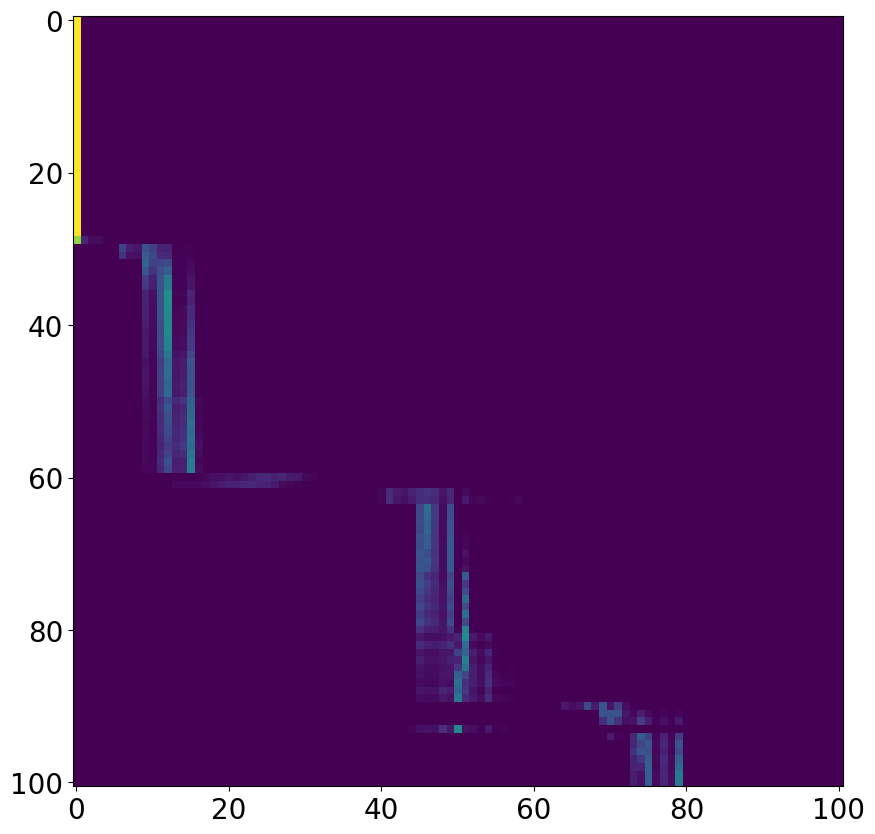
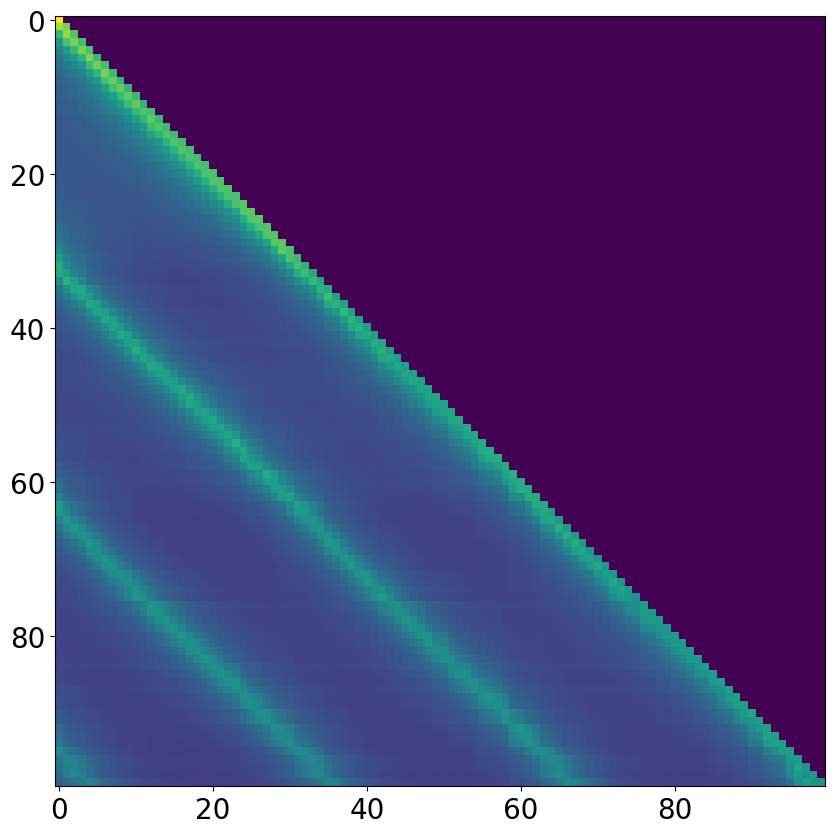
Figure 3: Comparison of attention matrices: (a) first layer of standard attention, (b) second layer of standard attention, (c) single layer of AFA, showing interpretable periodic structure.

---

Radial-Tangential Model and Geometric Extensions

The paper extends the SDE model to allow for separate radial and tangential noise covariances, leading to a more expressive class of models. The propagated covariance in this case is a diagonal plus rank-1 matrix, efficiently invertible via the Sherman-Morrison formula. The resulting attention mechanism performs separate precision-weighted updates for magnitude and direction, with geodesic steps on the hypersphere, closely paralleling the structure of Transformer layers with normalization.

This geometric perspective provides a theoretical explanation for the effectiveness of normalization and attention in Transformers, suggesting that they approximate MLE filtering on a hypersphere with unitary dynamics.

---

Connections to Prior Work

AFA unifies and extends several lines of research:

• Kalman filtering and robust adaptive filtering: By deriving attention as a robustified MLE for SDEs, AFA generalizes classical filtering to the parallel, non-recursive setting of attention.
• State space models and SSM-based sequence models: The use of diagonalizable SDEs and efficient covariance propagation connects AFA to S4, Mamba, and related SSM architectures, but with explicit uncertainty modeling.
• Probabilistic and kernel-based attention: The Mahalanobis distance-based similarity and precision-weighted aggregation relate AFA to probabilistic attention mechanisms and kernelized attention.
• Geometric and dynamical systems perspectives: The radial-tangential decomposition and geodesic updates provide a geometric interpretation of attention and normalization, aligning with recent work on the geometry of Transformer representations.

---

Implications and Future Directions

AFA provides a principled, interpretable, and robust alternative to standard attention, with several important implications:

• Improved uncertainty modeling: Explicit propagation of uncertainty enables more reliable filtering and prediction, especially in noisy or partially observed settings.
• Structured inductive bias: The incorporation of learnable dynamics restores temporal structure and regularization, potentially improving generalization and sample efficiency.
• Interpretability: The attention weights have a clear probabilistic interpretation as propagated precisions, facilitating analysis and debugging.
• Scalability: The closed-form and convolutional representations enable efficient implementation, with complexity matching standard attention under suitable assumptions.

Potential future developments include:

• Extension to nonlinear and non-Gaussian dynamics via neural SDEs or variational approximations.
• Application to real-world time series, control, and reinforcement learning tasks.
• Integration with diffusion models and score-based generative modeling.
• Exploration of hybrid recursive-parallel architectures for efficient online inference.

---

Conclusion

"Attention as an Adaptive Filter" establishes a rigorous connection between attention mechanisms and adaptive filtering for linear SDEs, providing both theoretical insights and practical algorithms. By grounding attention in the principles of robust state estimation and uncertainty propagation, AFA offers a compelling framework for structured, interpretable, and robust sequence modeling. The approach bridges the gap between classical control theory and modern deep learning, opening new avenues for principled, dynamics-aware attention architectures.