Sparse Autoencoder Neural Operators: Model Recovery in Function Spaces (2509.03738v1)

Abstract: We frame the problem of unifying representations in neural models as one of sparse model recovery and introduce a framework that extends sparse autoencoders (SAEs) to lifted spaces and infinite-dimensional function spaces, enabling mechanistic interpretability of large neural operators (NO). While the Platonic Representation Hypothesis suggests that neural networks converge to similar representations across architectures, the representational properties of neural operators remain underexplored despite their growing importance in scientific computing. We compare the inference and training dynamics of SAEs, lifted-SAE, and SAE neural operators. We highlight how lifting and operator modules introduce beneficial inductive biases, enabling faster recovery, improved recovery of smooth concepts, and robust inference across varying resolutions, a property unique to neural operators.

• The paper introduces a unified sparse model recovery framework that extends autoencoders to infinite-dimensional function spaces.
• It shows that lifting modules accelerate learning by acting as preconditioners that reduce dictionary atom correlation.
• Experiments with SAE-FNOs reveal robustness to resolution changes and effective recovery of smooth, interpretable concepts.

Sparse Autoencoder Neural Operators: Model Recovery in Function Spaces

Introduction and Motivation

The paper addresses the unification of representation learning across neural architectures, extending the analysis from finite-dimensional Euclidean spaces to infinite-dimensional function spaces via neural operators (NOs). The central question is whether the Platonic Representation Hypothesis (PRH)—which posits that different neural architectures converge to similar representations—extends to neural operators, which are increasingly important in scientific computing and neuroscience. The authors frame this as a sparse model recovery problem, leveraging sparse autoencoders (SAEs) and their extensions to function spaces to paper mechanistic interpretability and concept learning in both standard neural networks and neural operators.

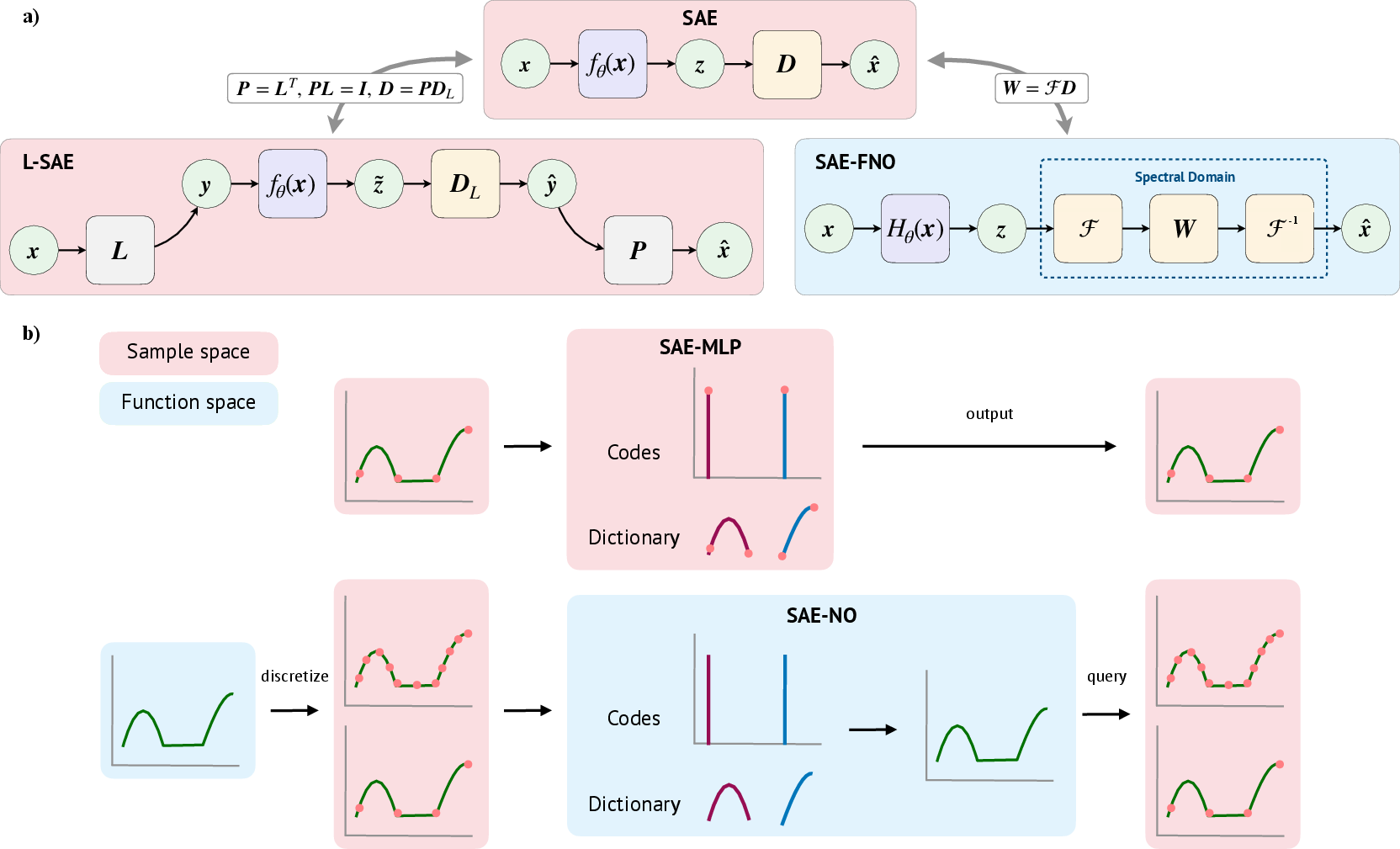
Figure 1: Model Recovery with SAEs. a) Architectural comparison. b) Euclidean vs. function spaces.

Theoretical Framework

Sparse Model Recovery and Autoencoders

The paper formalizes sparse model recovery as a bilevel optimization problem, where the goal is to recover an unknown overcomplete dictionary $D^*$ (or operator $\mathcal{G}_{D^*}$ in function spaces) that generates data from sparse latent codes. The standard SAE framework is extended to:

• Lifted SAEs (L-SAEs): Learning in a higher-dimensional lifted space, with lifting and projection operators.
• SAE Neural Operators (SAE-NO): Extending SAEs to infinite-dimensional function spaces, with encoders and decoders as operators.

The authors provide formal definitions for sparse generative models, sparse functional generative models, and their respective recovery problems, establishing a rigorous foundation for comparing representation recovery across architectures and domains.

Lifting and Operator Modules

A key contribution is the analysis of lifting modules, which map data into higher-dimensional spaces before encoding. Theoretical results show that lifting acts as a preconditioner, reducing dictionary atom correlation and promoting a more isotropic loss landscape, thereby accelerating learning. When lifting and projection are tied and orthogonal, the training dynamics and inference of L-SAEs reduce to those of standard SAEs.

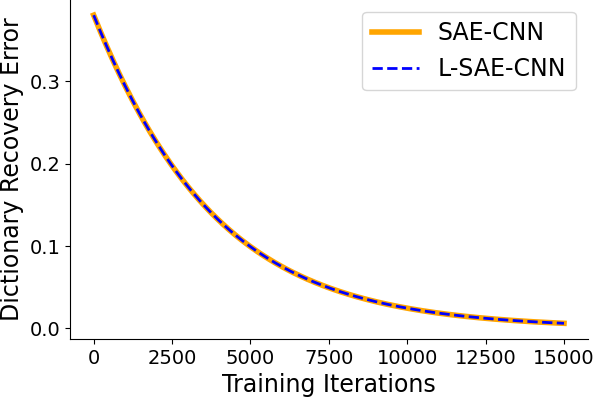
Figure 2: Lifting. Learning when $^{\text{T}} = L$.

Experimental Results

Lifting Accelerates Model Recovery

Empirical results on synthetic data generated from sparse convolutional generative models demonstrate that lifting accelerates model recovery for both dense and convolutional SAEs. The reduction in dictionary error and faster convergence are attributed to the preconditioning effect of lifting.

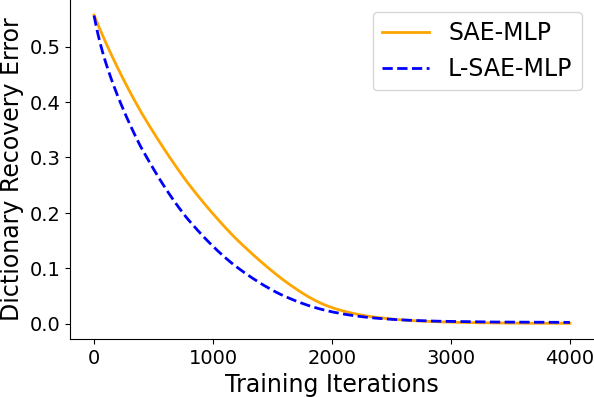
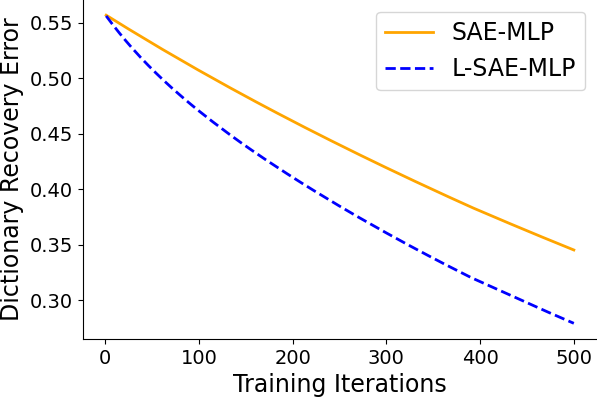
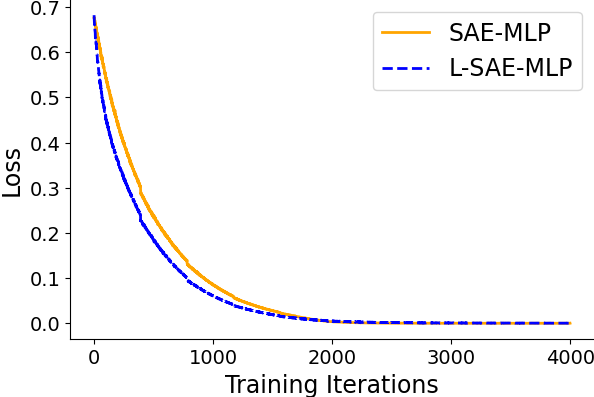
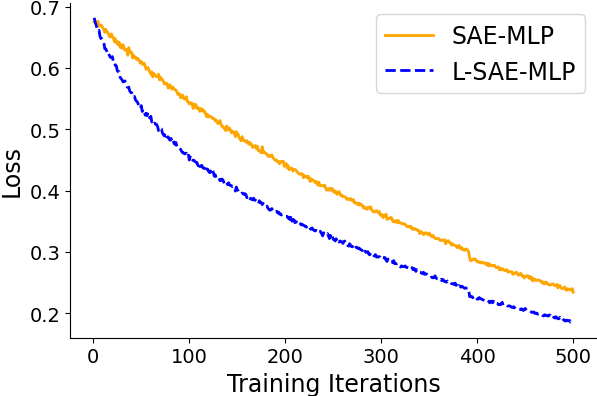
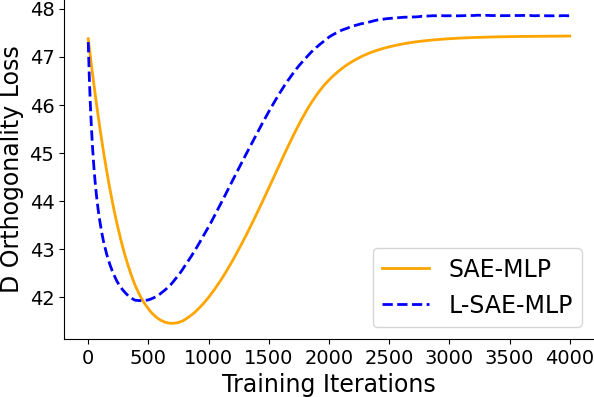
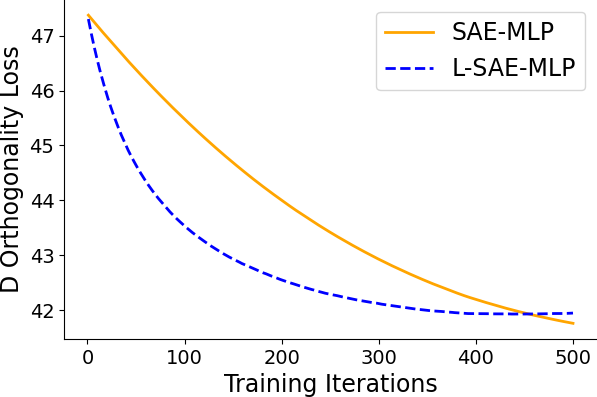
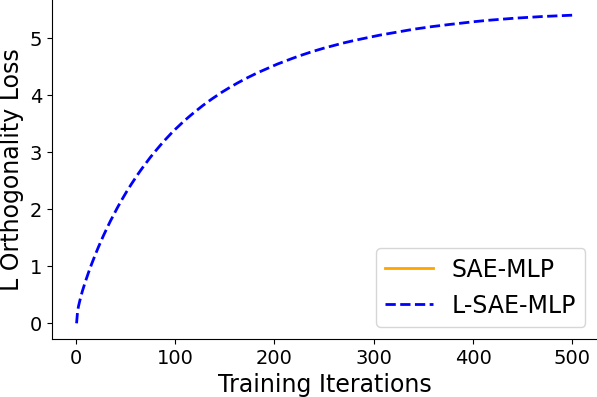
Figure 3: Dictionary error decreases more rapidly with lifting, indicating accelerated model recovery.

Model Recovery in Function Spaces

The extension to function spaces is realized via SAE-FNOs (Fourier Neural Operators). The experiments show:

• Lifting-induced acceleration persists in the operator setting, with L-SAE-FNOs converging faster than their non-lifted counterparts.
• Inductive bias for smooth concepts: SAE-FNOs with truncated frequency modes preferentially recover smooth concepts, which is advantageous when the underlying data is smooth.
• Robustness to resolution changes: SAE-FNOs can recover representations from higher-resolution data, whereas standard SAEs fail under resolution shifts.

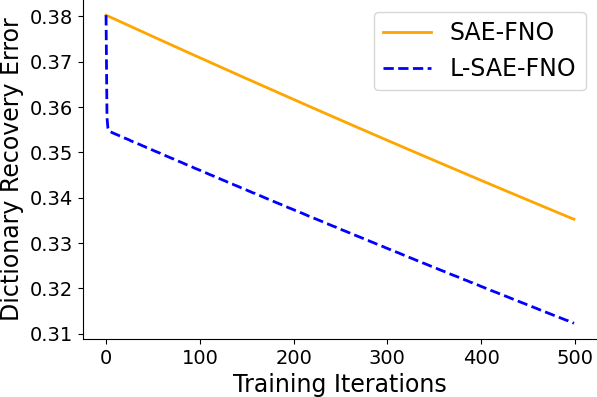
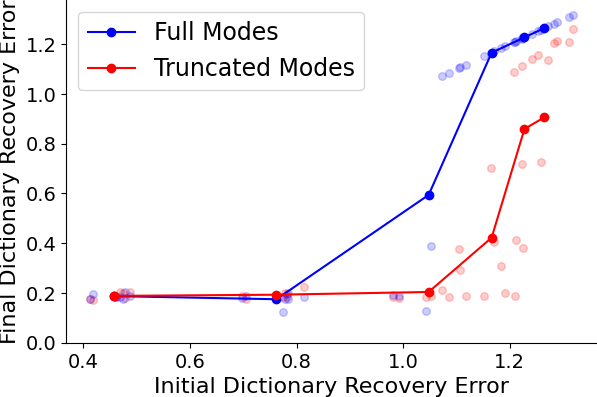
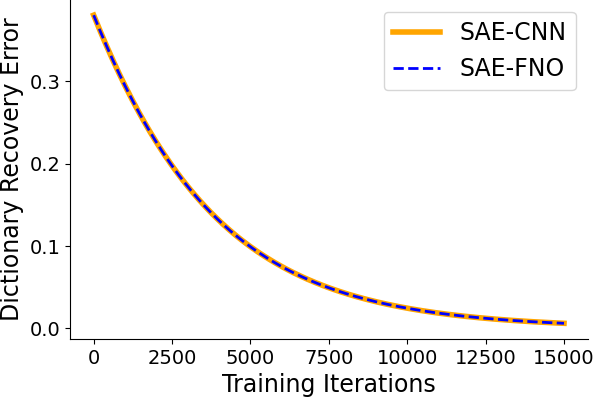
Figure 4: Lifting-accelerated learning continues to hold for operators.

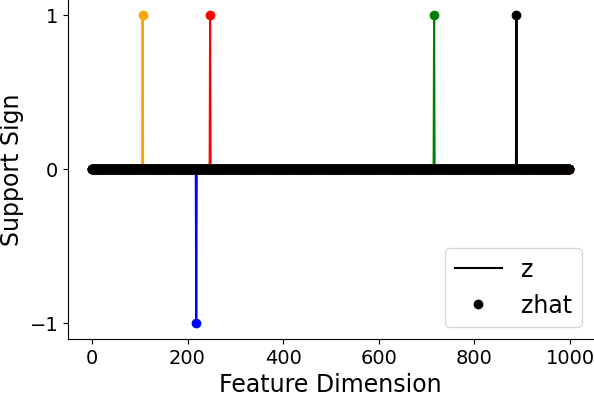
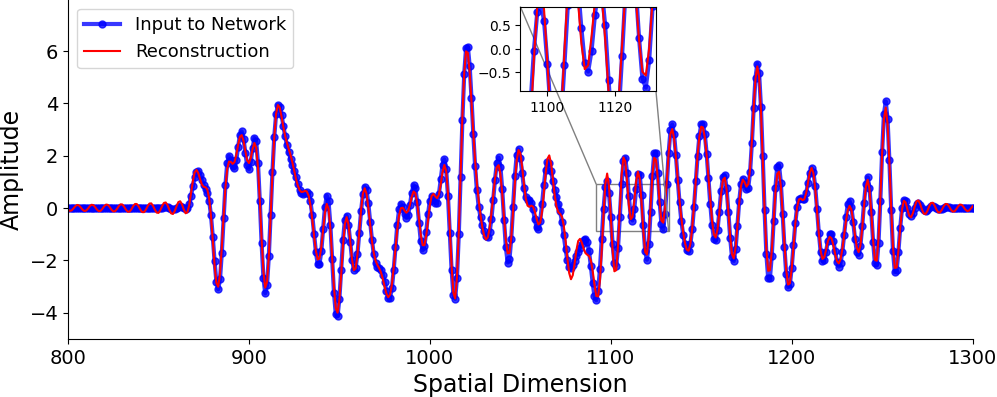
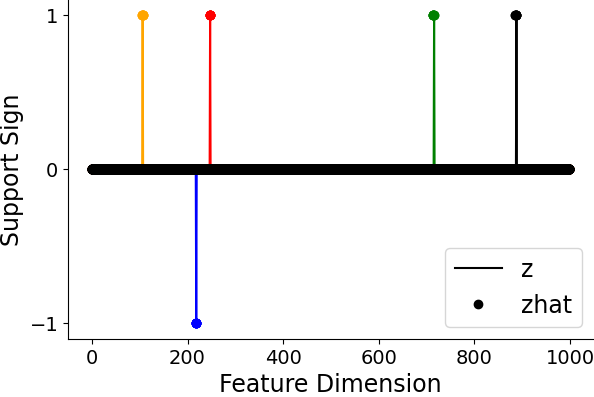
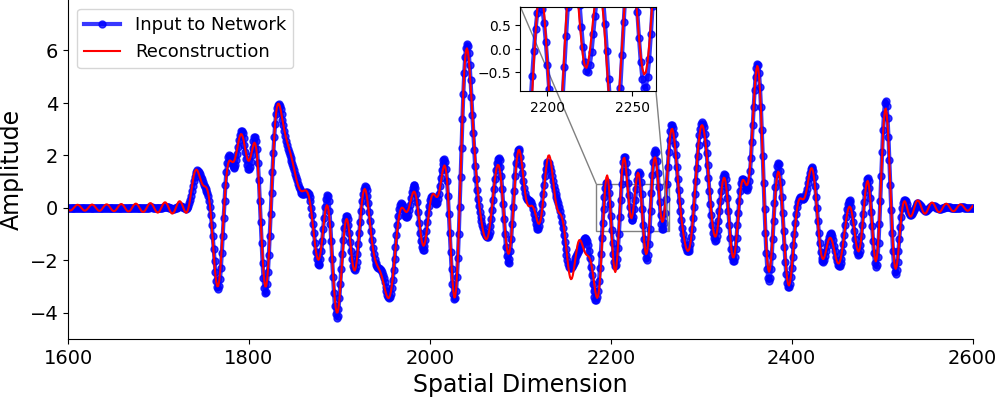
Figure 5: SAE-FNO can successfully infer the underlying sparse representations and reconstruct the data at varying sampling rates, demonstrating robustness to resolution changes.

Architectural and Training Dynamics Equivalence

Theoretical and empirical results establish that, under certain conditions (full-frequency filters, matched spatial support), the architectural inference and training dynamics of SAE-FNOs reduce to those of SAE-CNNs, with weights related by a Fourier transform. This equivalence is formalized in the paper's propositions and demonstrated in the experiments.

Implications and Future Directions

The framework unifies sparse model recovery across finite- and infinite-dimensional settings, providing a rigorous basis for mechanistic interpretability in neural operators. The results indicate that neural operators, particularly SAE-FNOs, possess inductive biases that are beneficial for recovering smooth and resolution-robust concepts—properties that are not shared by standard SAEs. This has significant implications for scientific modeling, where data often resides in function spaces and exhibits multi-scale structure.

The theoretical equivalence between lifted and standard architectures, as well as between convolutional and operator-based SAEs, suggests that insights and techniques from one domain can be transferred to the other. The robustness of SAE-FNOs to resolution changes is particularly relevant for applications in scientific computing, medical imaging, and neuroscience, where data discretization varies.

Future work should focus on applying this framework to real-world datasets, validating the practical utility of SAE-FNOs for extracting interpretable and physically meaningful concepts from large-scale neural operator models. There is also scope for further theoretical analysis of the implicit regularization induced by lifting and operator modules, and for exploring the limits of the PRH in more complex or non-linear operator settings.

Conclusion

This paper provides a comprehensive theoretical and empirical analysis of sparse model recovery in both Euclidean and function spaces, introducing a unified framework that extends sparse autoencoders to neural operators. The results demonstrate that lifting and operator modules confer significant advantages in terms of learning dynamics, inductive bias, and robustness to resolution changes. These findings have important implications for the interpretability and applicability of neural operators in scientific and engineering domains, and open new avenues for research at the intersection of sparse modeling, operator learning, and mechanistic interpretability.