Understanding sparse autoencoder scaling in the presence of feature manifolds (2509.02565v2)

Abstract: Sparse autoencoders (SAEs) model the activations of a neural network as linear combinations of sparsely occurring directions of variation (latents). The ability of SAEs to reconstruct activations follows scaling laws w.r.t. the number of latents. In this work, we adapt a capacity-allocation model from the neural scaling literature (Brill, 2024) to understand SAE scaling, and in particular, to understand how "feature manifolds" (multi-dimensional features) influence scaling behavior. Consistent with prior work, the model recovers distinct scaling regimes. Notably, in one regime, feature manifolds have the pathological effect of causing SAEs to learn far fewer features in data than there are latents in the SAE. We provide some preliminary discussion on whether or not SAEs are in this pathological regime in the wild.

• The paper demonstrates that SAE optimization can be framed as a latent allocation problem, linking feature frequency power laws to reconstruction loss scaling.
• It identifies a threshold where, if the loss decay rate (β) is lower than the feature frequency exponent (α), SAEs over-allocate latents to common manifolds, hindering rare feature discovery.
• Empirical analysis on synthetic and real data shows that manifold geometry critically influences latent allocation, offering insights for improving interpretability in large-scale models.

Scaling Laws and Pathological Regimes in Sparse Autoencoders with Feature Manifolds

Introduction

This paper presents a formal analysis of scaling laws in sparse autoencoders (SAEs), focusing on the impact of feature manifolds—multi-dimensional features—on SAE scaling behavior. The authors adapt a capacity-allocation model from neural scaling literature to the SAE context, providing a framework for understanding how SAEs allocate latents to features and how this allocation can lead to pathological scaling regimes. The work is motivated by empirical observations that SAEs, when scaled to large numbers of latents, exhibit predictable power-law improvements in reconstruction loss, but may fail to discover rare or complex features due to architectural and optimization biases.

Formal Model of SAE Scaling

The analysis begins by assuming that neural activations are generated as sparse linear combinations of features, each potentially living in a subspace of the activation space. The SAE is modeled as reconstructing activations via a sum of sparsely activating latents, with a loss function combining reconstruction error and a sparsity penalty (typically L1 or L0).

A key assumption is that SAE optimization reduces to a latent allocation problem: each latent is specific to a feature, and the total expected loss is a sum over per-feature losses, weighted by feature frequency. The optimization objective is thus to allocate a fixed number of latents across features to minimize total expected loss, given the distribution of feature frequencies and the per-feature loss curves.

Discrete vs. Manifold Features

For discrete features (dimension one), the optimal allocation is straightforward: assign one latent to each of the most frequent features, resulting in a linear relationship between the number of latents and the number of features discovered. If feature frequencies follow a power law $p_i \propto i^{-(1+\alpha)}$, the total loss scales as $N^{-\alpha}$, matching empirical SAE scaling laws.

However, for feature manifolds (multi-dimensional features), the per-feature loss curve $L_i(n_i)$ can decrease gradually as more latents are allocated, allowing the SAE to "tile" the manifold with many latents. This can lead to a regime where the SAE allocates a disproportionate number of latents to common manifolds, potentially at the expense of discovering rarer features.

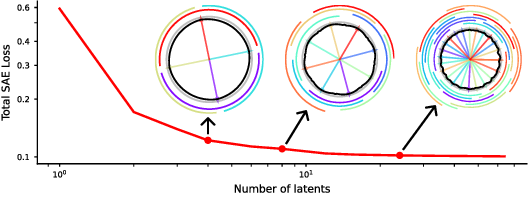
Figure 1: SAE scaling on a toy feature manifold $S^1$; SAEs tile the manifold with latents, reducing loss but potentially missing rare features.

Analytical Results: Power-Law Scaling and Pathological Regimes

The authors formalize the scaling behavior using power-law assumptions for both feature frequency ($\alpha$) and per-feature loss decay ($\beta$). The key result is a threshold phenomenon:

• If $\alpha < \beta$: SAE scaling is benign; the number of features discovered grows linearly with the number of latents, and loss scales as $N^{-\alpha}$.
• If $\beta < \alpha$: SAE scaling is pathological; the SAE allocates most latents to common manifolds, and the number of features discovered grows sublinearly, with loss scaling as $N^{-\beta}$.

Numerical simulations confirm that even a single feature manifold with slow loss decay can absorb the majority of latents in large SAEs, severely limiting feature discovery.

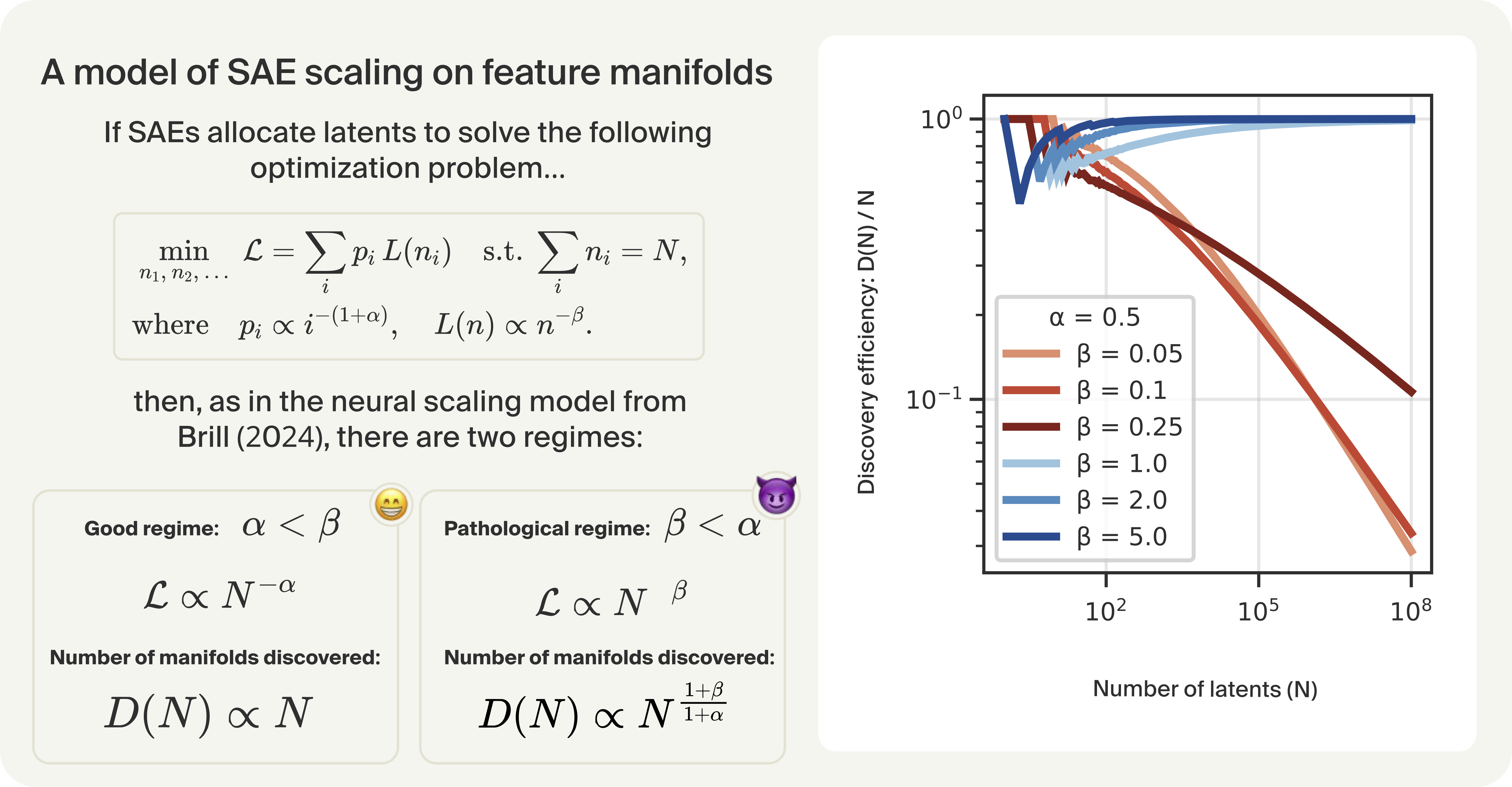
Figure 2: Application of Brill's capacity-allocation model to SAE scaling; simulation shows latent accumulation on a single manifold when $\beta < \alpha$.

Empirical Analysis: Synthetic and Real Data

Experiments on synthetic manifolds (e.g., hyperspheres) reveal that the shape of the $L(n)$ curve depends on manifold geometry. Some manifolds accommodate thousands of latents without saturating loss, while others plateau quickly. This suggests that the risk of pathological scaling depends critically on the geometry of feature manifolds in real neural networks.

Figure 3: ReLU SAE scaling on toy manifolds; $L(n)$ curves vary with feature geometry, affecting latent allocation.

The authors also analyze activation frequency distributions in large SAEs trained on LLMs (Gemma Scope) and vision models (Inception V1). They find power-law decay exponents for latent activation frequencies in the range $-0.57$ to $-0.74$, suggesting $\alpha \approx 0.5$–$0.7$. For synthetic hyperspheres, measured $\beta$ values are much lower ($\approx 0.05$ for $d=6$–$8$), indicating that pathological scaling could occur if real feature manifolds exhibit similar loss curves.

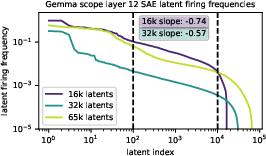
Figure 4: Latent activation frequencies in Gemma Scope SAEs; power-law decay exponents suggest $\alpha \approx 0.5$–$0.7$.

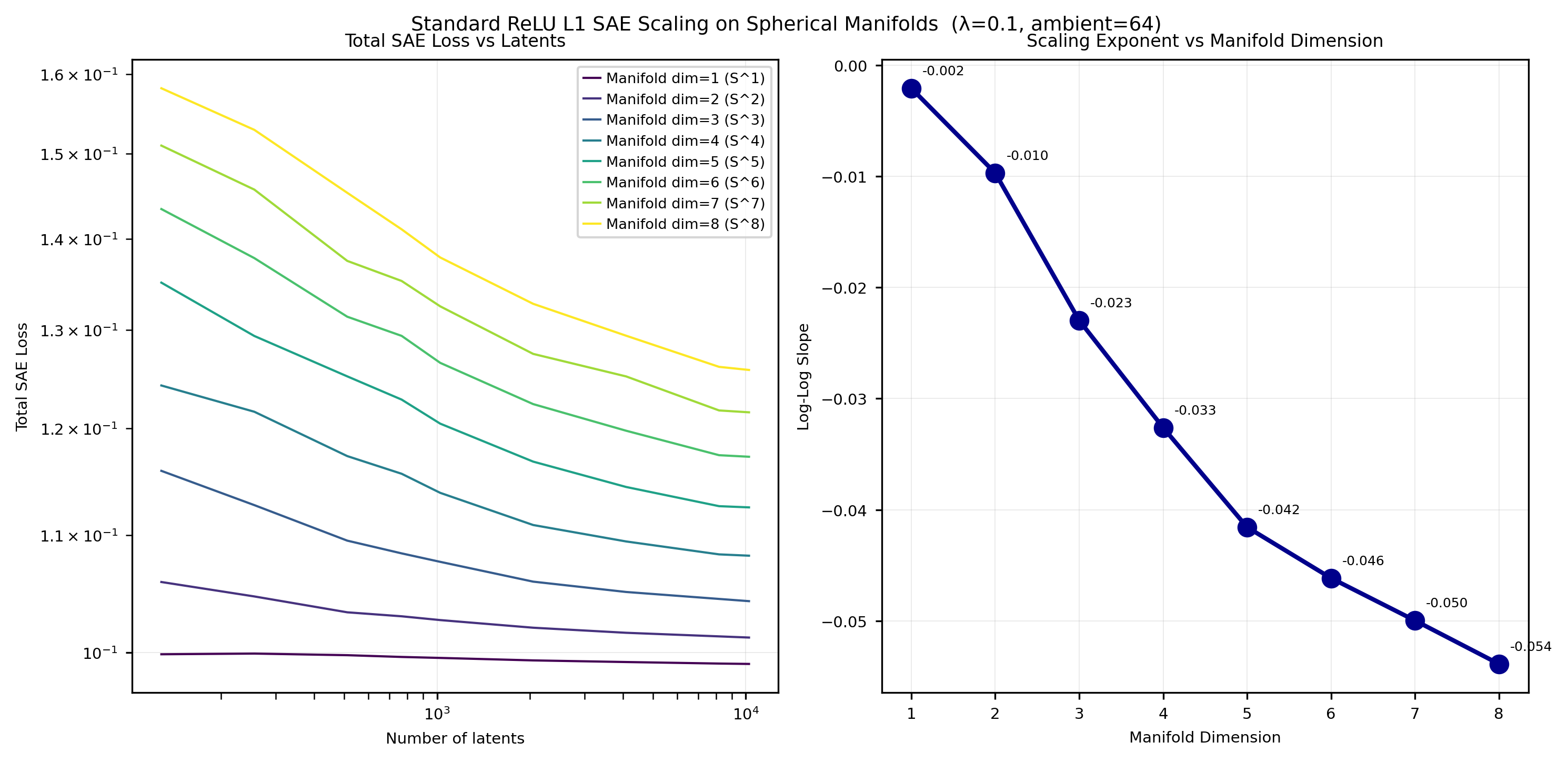
Figure 5: Measured slopes of $L_i$ curves for ReLU L1 SAEs on hyperspheres; $\beta$ is low for high-dimensional manifolds.

Feature Geometry and Latent Similarity

The paper investigates the geometry of SAE decoder latents, hypothesizing that tiling a low-dimensional manifold should result in high cosine similarity between decoder vectors. Analysis of Gemma Scope and Inception V1 SAEs shows some latents with high nearest-neighbor cosine similarity, but not in large numbers, and often associated with dead or duplicated latents rather than true manifold tiling.

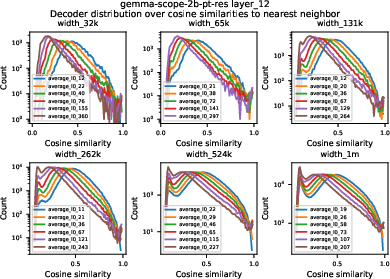
Figure 6: Distribution of nearest-neighbor cosine similarities for Gemma Scope SAEs; few latents exhibit extreme similarity.

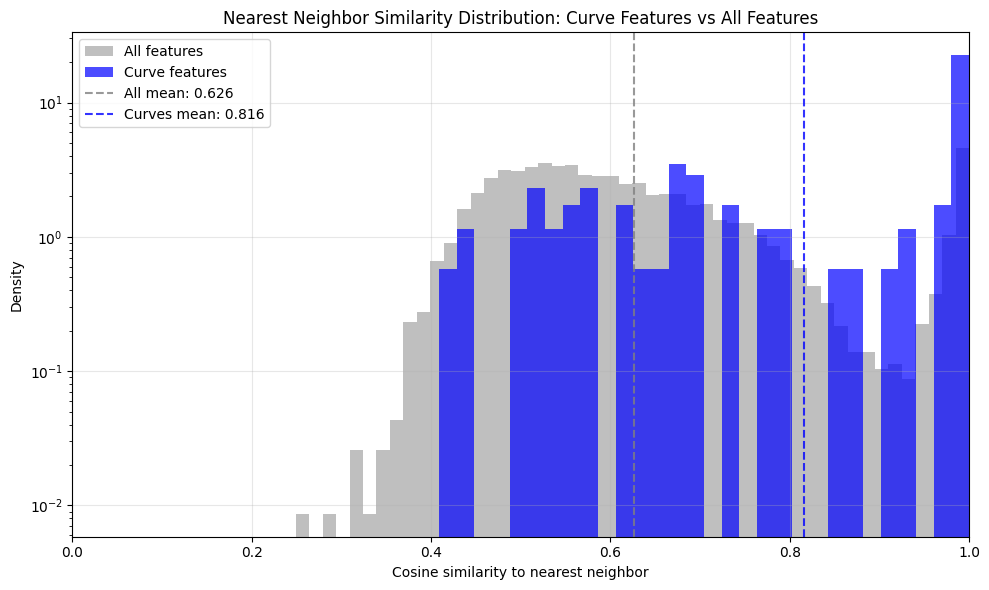
Figure 7: Pairwise cosine similarity distribution for Inception V1 SAEs; duplication may explain high similarity.

Implications and Future Directions

The formalism developed in this paper provides a principled framework for understanding SAE scaling in the presence of feature manifolds. The identification of a threshold between benign and pathological scaling regimes has significant implications for interpretability: in the pathological regime, SAEs may fail to discover rare or complex features, limiting their utility for mechanistic interpretability.

The empirical results suggest that the risk of pathological scaling depends on the true values of $\alpha$ and $\beta$ in real neural networks, which remain difficult to estimate. The geometry of feature manifolds—particularly the presence of variation in the radial direction—appears to mitigate the risk, as SAEs tend to learn basis solutions rather than tile manifolds extensively.

The work raises several open questions for future research:

• How can $\alpha$ and $\beta$ be robustly estimated in real-world neural networks?
• What architectural or training modifications can prevent pathological latent allocation?
• How do phenomena like feature absorption, compositionality, and manifold "ripples" affect SAE scaling and interpretability?

Conclusion

This paper advances the theoretical understanding of SAE scaling laws by framing SAE optimization as a latent allocation problem and analyzing the impact of feature manifolds on scaling behavior. The identification of a threshold between benign and pathological regimes provides a valuable lens for interpreting SAE performance and guiding future research. While empirical evidence suggests that pathological scaling may not be prevalent in practice, the framework developed here offers a foundation for further investigation into the geometry and frequency distribution of features in neural representations, with important implications for the interpretability and reliability of SAEs in large-scale models.