Understanding and Improving the Shampoo Optimizer via Kullback-Leibler Minimization (2509.03378v1)

Abstract: As an adaptive method, Shampoo employs a structured second-moment estimation, and its effectiveness has attracted growing attention. Prior work has primarily analyzed its estimation scheme through the Frobenius norm. Motivated by the natural connection between the second moment and a covariance matrix, we propose studying Shampoo's estimation as covariance estimation through the lens of Kullback-Leibler (KL) minimization. This alternative perspective reveals a previously hidden limitation, motivating improvements to Shampoo's design. Building on this insight, we develop a practical estimation scheme, termed KL-Shampoo, that eliminates Shampoo's reliance on Adam for stabilization, thereby removing the additional memory overhead introduced by Adam. Preliminary results show that KL-Shampoo improves Shampoo's performance, enabling it to stabilize without Adam and even outperform its Adam-stabilized variant, SOAP, in neural network pretraining.

• The paper reinterprets Shampoo’s second-moment estimation as a KL divergence minimization problem to derive a more principled optimizer.
• It introduces KL-Shampoo, which eliminates the need for Adam-based step-size grafting and achieves improved stability and computational efficiency.
• Experimental results on large-scale language models demonstrate that KL-Shampoo reduces memory footprint and generalizes well to tensor-valued weights.

A KL Perspective on Shampoo: Theory, Implementation, and Empirical Advances

Introduction

This paper presents a novel theoretical and algorithmic perspective on the Shampoo optimizer, a structured second-order method widely used for neural network training. The authors reinterpret Shampoo's Kronecker-factored second-moment estimation as a covariance estimation problem, proposing Kullback-Leibler (KL) divergence minimization as a more principled objective than the Frobenius norm. This shift in perspective exposes a fundamental limitation in the original Shampoo estimation scheme and motivates the development of KL-Shampoo, a new optimizer that eliminates the need for Adam-based step-size grafting and achieves improved stability and efficiency.

Theoretical Framework: KL Divergence for Covariance Estimation

The core insight is to treat the second-moment matrix of gradients as a covariance matrix and to seek a Kronecker-structured approximation that minimizes the KL divergence between the true and estimated Gaussian distributions. The KL divergence between two zero-mean Gaussians with covariances $A$ and $B$ is:

$$\mathrm{KL}(A, B) = \frac{1}{2} \left( \log \det B - \log \det A + \mathrm{Tr}(B^{-1}A) - d \right)$$

where $d$ is the dimensionality. This objective naturally respects the symmetric positive-definite (SPD) constraint required for preconditioners, unlike the Frobenius norm.

The authors show that the original Shampoo update, which alternates updates to the Kronecker factors while holding the other fixed, is only optimal for a one-sided KL minimization. When both factors are updated jointly, the optimal solution is given by a pair of coupled fixed-point equations:

$$A^* = \frac{1}{d_b} \mathbb{E}[ (B^*)^{-1} GG^\top ], \quad B^* = \frac{1}{d_a} \mathbb{E}[ G^\top (A^*)^{-1} G ]$$

where $G$ is the matrix gradient, and $d_a, d_b$ are the dimensions of the Kronecker factors. This motivates a new moving-average update that simultaneously refines both factors, leading to the KL-Shampoo algorithm.

Algorithmic Advances: KL-Shampoo and Efficient Implementation

The idealized KL-Shampoo update requires matrix inversions and eigen decompositions at every step, which are computationally prohibitive. To address this, the authors propose:

• Moving-average updates for the Kronecker factors, using the most recent estimates of the other factor for inversion.
• Eigenvalue estimation using an outdated eigenbasis, allowing for infrequent (every $T$ steps) QR decompositions instead of expensive eigen decompositions.
• Preconditioning using the Kronecker product of the estimated factors, with elementwise operations on the eigenvalues for efficiency.

This approach enables KL-Shampoo to match the computational profile of SOAP (an Adam-stabilized Shampoo variant) while using less memory and avoiding the need for step-size grafting.

The following pseudocode summarizes the KL-Shampoo update with QR-based eigenbasis estimation:

for each iteration: G = compute_gradient() # Update Kronecker factors with moving average and matrix inversion A = (1 - beta2) * A + (beta2 / d_b) * (B_inv @ G @ G.T) B = (1 - beta2) * B + (beta2 / d_a) * (G.T @ A_inv @ G) # Every T steps, update eigenbasis using QR decomposition if step % T == 0: Q_A, _ = qr_decomposition(A) Q_B, _ = qr_decomposition(B) # Estimate eigenvalues in the (possibly outdated) eigenbasis lambda_A = diag(Q_A.T @ A @ Q_A) lambda_B = diag(Q_B.T @ B @ Q_B) # Precondition gradient preconditioned_grad = -gamma * (Q_A @ diag(lambda_A ** -0.5) @ Q_A.T) @ G @ (Q_B @ diag(lambda_B ** -0.5) @ Q_B.T)

Empirical Results

The authors conduct extensive experiments on four LLMs (NanoGPT, NanoRWKV7, Llama, and NanoMoE) using large-scale datasets and strong baselines, including Shampoo with various powers and SOAP. Hyperparameters are tuned via random search with 120 runs per method.

Key empirical findings:

• KL-Shampoo eliminates the need for Adam-based step-size grafting. Shampoo without grafting fails to train certain models (e.g., RWKV7), while KL-Shampoo remains stable and effective.

  Figure 1: KL-Shampoo removes the need for step-size grafting with Adam; Shampoo without grafting fails to train RWKV7 in all 120 runs.

• KL-Shampoo matches or exceeds the efficiency of SOAP while using less memory and computational resources, due to the efficient QR-based implementation.

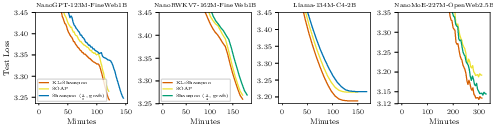
  Figure 2: KL-Shampoo meets or exceeds SOAP's efficiency using QR decomposition, with the best Shampoo run included for comparison.

• KL-Shampoo generalizes to tensor-valued weights (e.g., in NanoMoE) without loss of flexibility, as the KL framework extends naturally to higher-order tensors.

Practical Implications and Limitations

The KL-based perspective provides a principled foundation for structured preconditioning in adaptive optimizers. KL-Shampoo offers:

• Improved stability without auxiliary optimizers or grafting.
• Reduced memory footprint compared to SOAP, as it avoids storing additional diagonal statistics.
• Computational efficiency via QR-based eigenbasis estimation and moving-average eigenvalue updates.

However, the method still requires periodic QR decompositions and matrix inversions, which may be nontrivial for very large layers. The moving-average scheme introduces a lag in the estimation of the Kronecker factors, which could affect convergence in highly nonstationary regimes. Further, the approach assumes the covariance structure of gradients is well-approximated by a Kronecker product, which may not hold in all architectures.

Theoretical and Future Directions

The KL minimization framework unifies and extends previous analyses of Shampoo and its variants. It suggests several avenues for future research:

• Extension to block-diagonal or more general structured preconditioners using KL divergence as the objective.
• Adaptive frequency of QR/eigenbasis updates based on the rate of change in the Kronecker factors.
• Integration with low-rank or sketching techniques to further reduce computational overhead.
• Analysis of convergence and generalization properties under the KL-based updates, especially in the presence of non-Gaussian gradient distributions.

Conclusion

By reinterpreting Shampoo's second-moment estimation as a KL divergence minimization problem, this work identifies a key limitation in the original algorithm and introduces KL-Shampoo, a practical and theoretically motivated optimizer. KL-Shampoo achieves improved stability and efficiency, obviates the need for Adam-based grafting, and generalizes to tensor-valued weights. The KL perspective provides a principled foundation for future advances in structured adaptive optimization.