Calibration Prediction Interval for Non-parametric Regression and Neural Networks (2509.02735v1)

Abstract: Accurate conditional prediction in the regression setting plays an important role in many real-world problems. Typically, a point prediction often falls short since no attempt is made to quantify the prediction accuracy. Classically, under the normality and linearity assumptions, the Prediction Interval (PI) for the response variable can be determined routinely based on the $t$ distribution. Unfortunately, these two assumptions are rarely met in practice. To fully avoid these two conditions, we develop a so-called calibration PI (cPI) which leverages estimations by Deep Neural Networks (DNN) or kernel methods. Moreover, the cPI can be easily adjusted to capture the estimation variability within the prediction procedure, which is a crucial error source often ignored in practice. Under regular assumptions, we verify that our cPI has an asymptotically valid coverage rate. We also demonstrate that cPI based on the kernel method ensures a coverage rate with a high probability when the sample size is large. Besides, with several conditions, the cPI based on DNN works even with finite samples. A comprehensive simulation study supports the usefulness of cPI, and the convincing performance of cPI with a short sample is confirmed with two empirical datasets.

• The paper introduces a calibration framework that compensates for estimation variability in prediction intervals.
• It leverages both DNN and kernel estimators with monotonicity corrections to achieve asymptotically valid and finite-sample coverage.
• Empirical results demonstrate that adjusted DNN-based cPIs outperform classical methods, especially in small-sample settings.

Calibration Prediction Intervals for Non-parametric Regression and Neural Networks

Overview and Motivation

This paper introduces a unified framework for constructing calibration prediction intervals (cPI) in regression settings, leveraging both deep neural networks (DNNs) and kernel-based non-parametric estimators. The central motivation is to address the limitations of classical prediction intervals (PIs), which typically rely on normality and linearity assumptions and fail to capture estimation variability, leading to systematic undercoverage in practical applications. The proposed cPI methodology is designed to be asymptotically valid, robust to model misspecification, and computationally efficient, with theoretical guarantees for both large-sample and, under certain conditions, finite-sample coverage.

Methodological Framework

Non-parametric Construction of Prediction Intervals

The paper formalizes two non-parametric approaches for PI construction:

1. Moment-based PI: Utilizes estimators of conditional mean and second moment, avoiding parametric assumptions. The interval is symmetric around the mean and is valid under normality if the estimators are consistent.
2. Quantile-based PI: Constructs intervals using estimated conditional quantiles derived from the estimated conditional cumulative distribution function (CDF), typically via kernel methods or quantile regression. This approach is more flexible but suffers from undercoverage due to ignored estimation variability.

Calibration via Estimation of Conditional CDF

The core innovation is the calibration step, which systematically compensates for estimation variability. The procedure involves:

• Discretizing the response variable $Y$ into a grid $\{q_j\}_{j=1}^g$.
• For each grid point, training a DNN (or kernel estimator) to approximate $\mathbb{E}[\mathbbm{1}(Y \leq q_j) | X]$, i.e., the conditional CDF at $q_j$.
• Applying monotonicity correction to the estimated CDF values to ensure valid quantile extraction (see Figure 1).

  Figure 1: The effects of three monotonicity corrections methods.

• Calibrating the PI by searching for grid indices $l$ and $r$ such that the difference in corrected CDF values meets or exceeds the desired coverage level $1-\alpha$, with options for symmetric or asymmetric intervals and minimal length optimization.

Algorithmic Implementation

The DNN-based cPI algorithm is highly parallelizable, requiring $g$ independent DNN trainings (one per grid point), which can be executed concurrently. Hyperparameters such as grid size, learning rate, batch size, and network architecture are shown to have limited impact on coverage, reducing the need for extensive tuning compared to deep generative approaches.

For kernel-based cPI, standard conditional density estimators are used, with bandwidth selection via cross-validation. The same calibration and monotonicity correction procedures apply.

Theoretical Guarantees

Asymptotic and Large-sample Coverage

The paper rigorously proves that both DNN- and kernel-based cPIs are asymptotically valid, i.e., the empirical coverage converges to the nominal level as $n \to \infty$ and grid size $g \to \infty$, under minimal regularity conditions. For kernel estimators, a non-asymptotic error bound is established, guaranteeing high-probability coverage for sufficiently large samples.

Finite-sample Coverage

A notable contribution is the demonstration that, under oracle estimation and appropriate grid spacing, the adjusted cPI can guarantee coverage even in finite samples. This is achieved by expanding the interval endpoints to compensate for estimation error, with theoretical bounds derived from the modulus of continuity of the target function and DNN approximation rates.

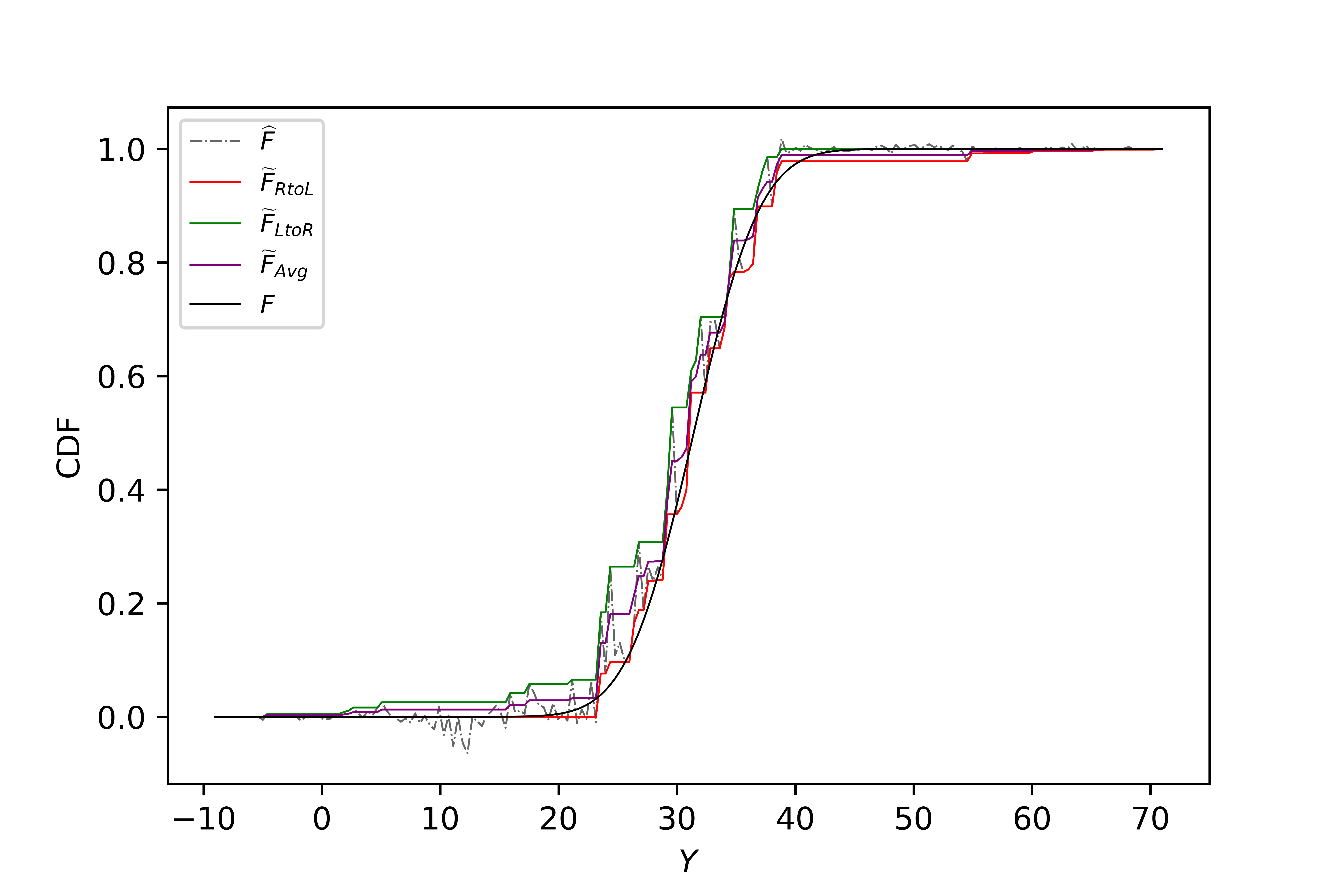
Monotonicity Correction

Three correction methods (left-to-right, right-to-left, and average) are proposed and analyzed. The average correction is empirically shown to best mimic the oracle CDF, especially in the tails, and is recommended for practical use.

Empirical Evaluation

Simulation Studies

Extensive simulations across six nonlinear regression models (homoscedastic and heteroscedastic, with normal, $t$, and skew-normal errors) demonstrate:

• Classical PIs systematically under-cover, even under normality and large samples.
• cPIs, especially the asymmetric average-corrected variant, achieve coverage rates close to nominal with shorter interval lengths.
• Increasing DNN width improves performance up to a point, but double descent phenomena may occur.
• Adjusted cPIs reliably correct undercoverage in small samples.

Real Data Analysis

On the UCI wine quality datasets (red and white), cPIs are compared against deep generative PIs (quantile, pertinent, adversarial KL, adversarial Wasserstein):

• cPIs with DNN estimators outperform kernel-based variants and deep generative methods in both coverage and interval length.
• Adjusted cPIs are robust to small training sizes and grid parameter choices.
• Kernel-based cPIs treating $Y$ as ordered-discrete outperform continuous variants in practice.

Practical and Theoretical Implications

The cPI framework provides a robust, unified approach to uncertainty quantification in regression, applicable to both classical non-parametric and modern neural network estimators. Its parallelizable architecture and minimal tuning requirements make it suitable for large-scale deployment. The theoretical results clarify the conditions under which coverage guarantees can be made, including the rarely addressed finite-sample regime.

The monotonicity correction methodology is of independent interest for CDF estimation in non-parametric settings. The empirical superiority of DNN-based cPIs over kernel methods provides further evidence for the resilience of neural networks to the curse of dimensionality.

Future Directions

Potential avenues for further research include:

• Extending the calibration framework to other neural architectures (e.g., convolutional, transformer-based models).
• Developing adaptive grid selection strategies to optimize interval length and coverage.
• Investigating the interplay between calibration and conformal prediction, especially in high-dimensional and structured data settings.
• Formalizing finite-sample coverage guarantees for DNN-based cPIs beyond oracle estimation.

Conclusion

This work establishes a theoretically sound and practically effective methodology for constructing calibration prediction intervals in regression, leveraging both DNNs and kernel estimators. The approach overcomes the limitations of classical PIs and deep generative methods, providing robust coverage guarantees and efficient computation. The adjusted cPI is particularly recommended for small-sample scenarios, and DNN-based cPIs are empirically superior in both simulated and real-world datasets. The framework is extensible and opens new directions for uncertainty quantification in modern machine learning.