Variational Uncertainty Decomposition for In-Context Learning (2509.02327v2)

Abstract: As LLMs gain popularity in conducting prediction tasks in-context, understanding the sources of uncertainty in in-context learning becomes essential to ensuring reliability. The recent hypothesis of in-context learning performing predictive Bayesian inference opens the avenue for Bayesian uncertainty estimation, particularly for decomposing uncertainty into epistemic uncertainty due to lack of in-context data and aleatoric uncertainty inherent in the in-context prediction task. However, the decomposition idea remains under-explored due to the intractability of the latent parameter posterior from the underlying Bayesian model. In this work, we introduce a variational uncertainty decomposition framework for in-context learning without explicitly sampling from the latent parameter posterior, by optimising auxiliary queries as probes to obtain an upper bound to the aleatoric uncertainty of an LLM's in-context learning procedure, which also induces a lower bound to the epistemic uncertainty. Through experiments on synthetic and real-world tasks, we show quantitatively and qualitatively that the decomposed uncertainties obtained from our method exhibit desirable properties of epistemic and aleatoric uncertainty.

• The paper introduces a variational framework that separates aleatoric and epistemic uncertainty in LLM in-context learning by optimizing auxiliary queries.
• It employs permutation-invariant inference to approximate Bayesian behavior, ensuring that predictive distributions remain consistent across input orderings.
• Empirical results demonstrate that as contextual data increases, epistemic uncertainty decreases while practical applications in bandit exploration and OOD detection improve.

Variational Uncertainty Decomposition for In-Context Learning

Motivation and Problem Formulation

The paper addresses the challenge of decomposing predictive uncertainty in LLMs during in-context learning (ICL), specifically distinguishing between epistemic uncertainty (model uncertainty due to limited data) and aleatoric uncertainty (irreducible data noise). The Bayesian interpretation of ICL posits that, when prompted with a dataset $\mathcal{D} = \{(x_i, y_i)\}_{i=1}^n$ and a test input $x^*$, the LLM implicitly infers a latent parameter $\theta$ and computes a posterior predictive $p(y^*|x^*, \mathcal{D})$. This enables, in principle, a decomposition of predictive uncertainty into epistemic and aleatoric components. However, the intractability of the implicit posterior $p(\theta|\mathcal{D})$ in LLMs, and the lack of exchangeability in autoregressive generation, make direct Bayesian decomposition infeasible.

Variational Uncertainty Decomposition (VUD) Framework

The core contribution is a variational framework for uncertainty decomposition that does not require explicit sampling from the latent parameter posterior. Instead, the method introduces optimizable auxiliary queries $Z$ (and their hypothetical responses $U$) appended to the context, and computes a variational upper bound to the aleatoric uncertainty by conditioning on $Z, U$. This construction yields a lower bound on epistemic uncertainty by subtraction from the total predictive uncertainty.

Figure 1: The VUD framework, showing the role of auxiliary queries $Z$ and their responses $U$ in bounding aleatoric uncertainty.

Formally, for a test input $x^*$, the variational aleatoric uncertainty is defined as:

$$V_a(y^* | x^*, Z, \mathcal{D}) := \mathbb{E}_{p(U|Z, \mathcal{D})}[\mathbb{H}[p(y^*|x^*, U, Z, \mathcal{D})]]$$

where the expectation is over the model's predictive distribution for $U$ given $Z$ and $\mathcal{D}$. The optimal $Z$ is found by minimizing $V_a$ over candidate queries, subject to a KL-divergence constraint ensuring that the conditional predictive distribution remains close to the original $p(y^*|x^*, \mathcal{D})$.

The total uncertainty is given by the entropy of the predictive distribution, and the epistemic uncertainty is estimated as the difference:

$$V_e(y^*|x^*, \mathcal{D}) := \mathbb{H}[p(y^*|x^*, \mathcal{D})] - \tilde{V}_a(y^*|x^*, \mathcal{D})$$

where $\tilde{V}_a$ is the clipped variational aleatoric uncertainty.

Implementation Details

Promoting Exchangeability

To approximate the exchangeability required for a Bayesian interpretation, the method ensembles predictions over random permutations of the in-context examples. For each permutation, the LLM is prompted with the permuted context and the test input, and the predictive distributions are averaged. This is critical for ensuring that the predictive rule is symmetric in the context, a necessary condition for de Finetti's theorem to apply.

Auxiliary Query Optimization

The search for optimal $Z$ is performed using several strategies:

• Perturbation: $Z$ is chosen as a small perturbation of $x^*$.
• Repetition: $Z = x^*$.
• Random Sampling: $Z$ is sampled randomly from the input domain.
• Bayesian Optimization: $Z$ is actively selected to minimize $V_a$.

KL filtering is applied to ensure that the conditional predictive distribution with $Z$ does not deviate excessively from the original, maintaining approximate Bayesian consistency.

Practical Algorithm

For classification, the predictive distribution is computed via token-level probabilities for each class, averaged over permutations. For regression, a Gaussian approximation is used, with the mean and variance estimated from multiple LLM samples. The marginalization over $U$ is performed by sampling possible responses and aggregating the resulting predictive distributions.

Empirical Results

Synthetic Data

The VUD framework is evaluated on synthetic regression and classification tasks, including 1D logistic regression, linear regression, the two-moons dataset, and a multi-class spirals dataset.

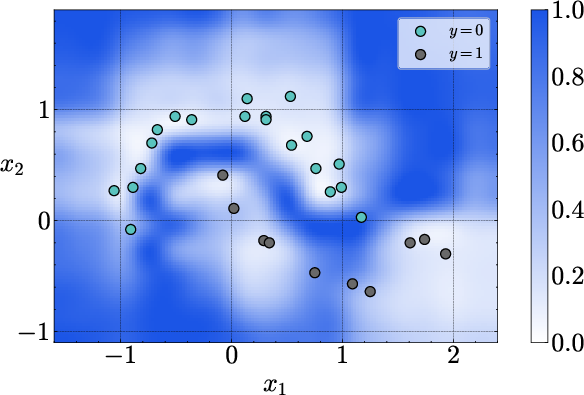
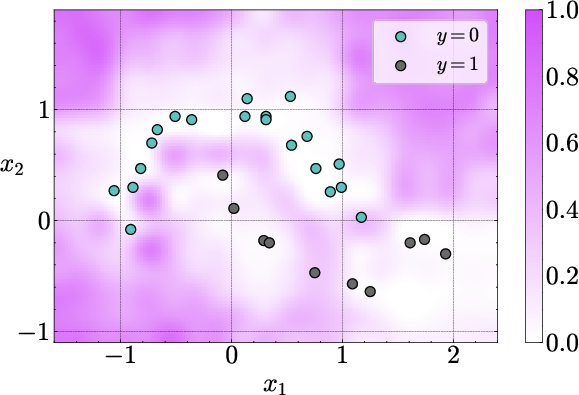
Figure 2: Uncertainty decomposition on the two-moons dataset. Aleatoric uncertainty is concentrated near the decision boundary, while epistemic uncertainty is high in regions far from the in-context data.

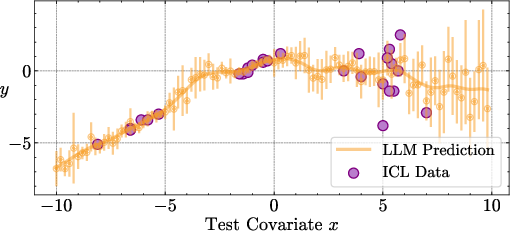
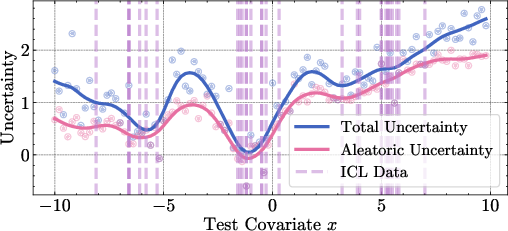
Figure 3: Predicted mean and standard deviation for regression with heteroscedastic noise, showing the model's ability to distinguish between data noise and lack of context.

The decomposed uncertainties exhibit the expected qualitative behavior: epistemic uncertainty is minimized near the in-context examples and increases in regions lacking data, while aleatoric uncertainty is localized near ambiguous or noisy regions.

Scaling with Data

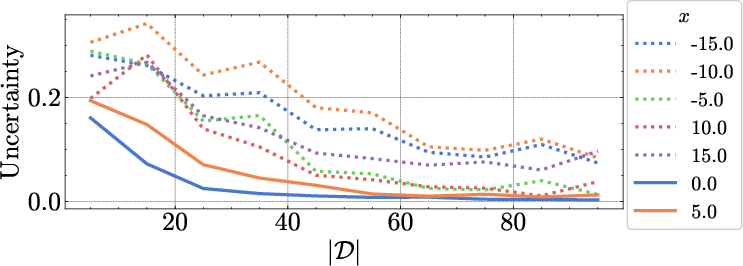
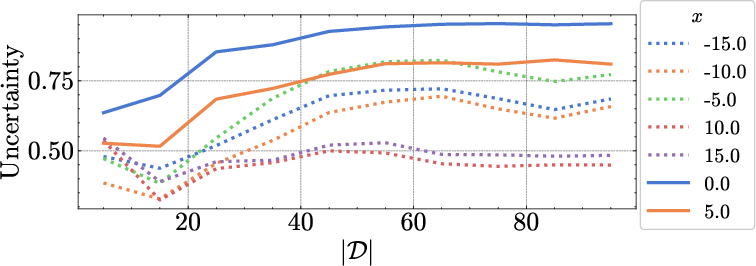
Figure 4: Epistemic uncertainty decreases as the size of the in-context dataset increases, while aleatoric uncertainty remains stable, consistent with Bayesian predictions.

Effect of Auxiliary Query Choice

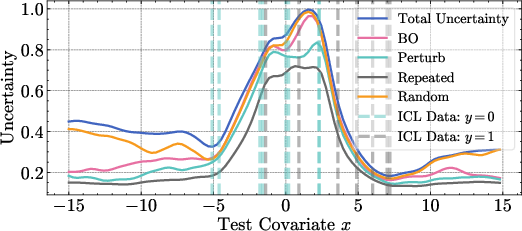
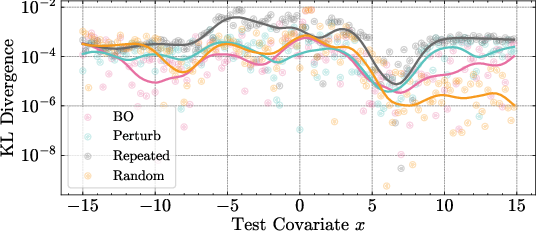
Figure 5: The choice of $Z$ affects the tightness of the aleatoric uncertainty bound and the KL divergence from the original predictive distribution. Perturbation and repetition strategies yield lower variational bounds.

Downstream Applications

Bandit Problems

The VUD epistemic uncertainty is used as the exploration bonus in UCB-style bandit algorithms. Empirically, using epistemic variance leads to lower regret and more robust exploration compared to using total variance, especially when the optimal arm has lower intrinsic noise.

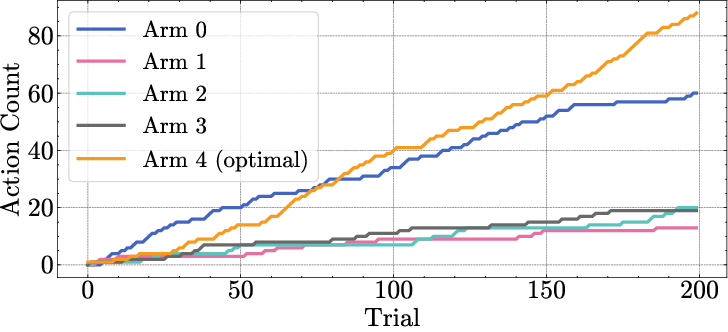
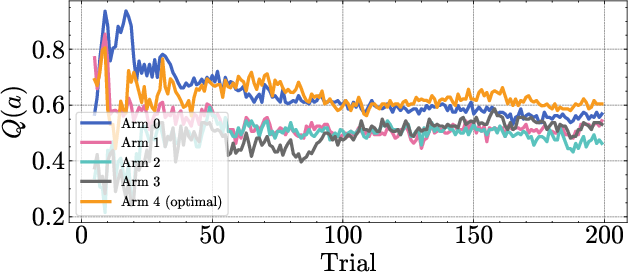
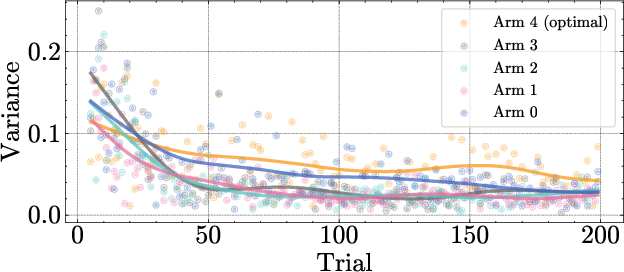
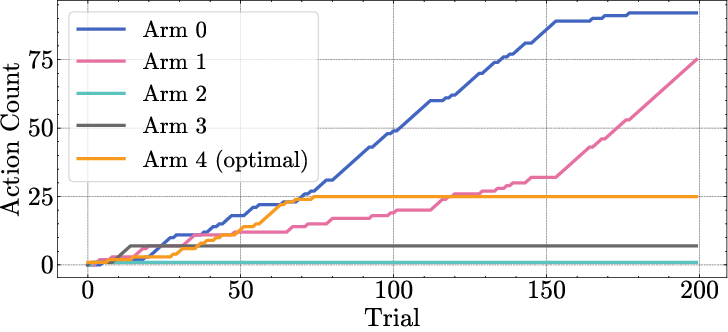
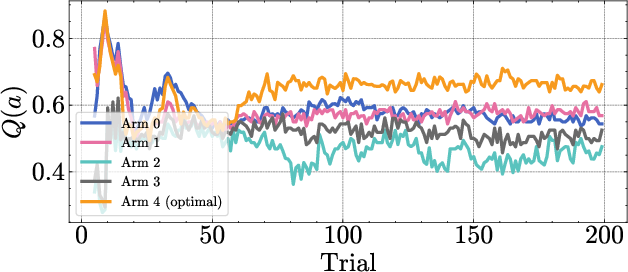
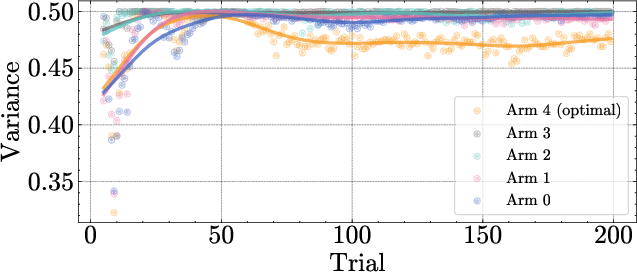
Figure 6: Cumulative arm counts in a bandit run, showing that epistemic variance leads to more consistent selection of the optimal arm.

Out-of-Distribution Detection

On question answering tasks, epistemic uncertainty from VUD yields higher AUC scores for OOD detection than total uncertainty in several settings, demonstrating the practical utility of the decomposition for reliability assessment.

Theoretical Guarantees and Limitations

The variational estimator provides a provable upper bound on aleatoric uncertainty and a lower bound on epistemic uncertainty, under the conditional independence assumptions encoded in the graphical model. The tightness of these bounds depends on the informativeness of the auxiliary queries and the degree to which the LLM's ICL behavior approximates Bayesian inference.

A key limitation is the reliance on the approximate Bayesian behavior of ICL, which may break down for long contexts or in non-exchangeable settings. The method is most reliable for short context lengths and when permutation invariance is enforced at inference.

Implications and Future Directions

The VUD framework enables principled, scalable uncertainty decomposition in LLMs without requiring explicit access to the latent parameter posterior. This advances the practical deployment of LLMs in settings where reliability and uncertainty quantification are critical, such as active learning, selective prediction, and safe exploration.

Future work should address:

• Extending the approach to open-ended natural language outputs, potentially integrating semantic uncertainty quantification.
• Improving the efficiency of auxiliary query optimization, especially in high-dimensional or structured input spaces.
• Investigating architectural or training modifications to further promote exchangeability and Bayesian behavior in LLMs.

Conclusion

The variational uncertainty decomposition framework provides a theoretically grounded and empirically validated approach for decomposing predictive uncertainty in LLM-based in-context learning. By leveraging auxiliary queries and permutation-invariant inference, the method enables robust estimation of epistemic and aleatoric uncertainty, facilitating downstream applications in exploration, OOD detection, and selective prediction. The approach is broadly applicable to any setting where the predictive distribution is implicitly defined and direct posterior sampling is infeasible.