DaCe AD: Unifying High-Performance Automatic Differentiation for Machine Learning and Scientific Computing (2509.02197v1)

Abstract: Automatic differentiation (AD) is a set of techniques that systematically applies the chain rule to compute the gradients of functions without requiring human intervention. Although the fundamentals of this technology were established decades ago, it is experiencing a renaissance as it plays a key role in efficiently computing gradients for backpropagation in machine learning algorithms. AD is also crucial for many applications in scientific computing domains, particularly emerging techniques that integrate machine learning models within scientific simulations and schemes. Existing AD frameworks have four main limitations: limited support of programming languages, requiring code modifications for AD compatibility, limited performance on scientific computing codes, and a naive store-all solution for forward-pass data required for gradient calculations. These limitations force domain scientists to manually compute the gradients for large problems. This work presents DaCe AD, a general, efficient automatic differentiation engine that requires no code modifications. DaCe AD uses a novel ILP-based algorithm to optimize the trade-off between storing and recomputing to achieve maximum performance within a given memory constraint. We showcase the generality of our method by applying it to NPBench, a suite of HPC benchmarks with diverse scientific computing patterns, where we outperform JAX, a Python framework with state-of-the-art general AD capabilities, by more than 92 times on average without requiring any code changes.

• The paper introduces DaCe AD, a unified automatic differentiation framework that leverages a data-centric IR to avoid code rewrites.
• It employs a novel ILP-based checkpointing algorithm to balance memory usage and recomputation costs for efficient gradient propagation.
• Experimental evaluations demonstrate significant speedups over JAX JIT, with performance gains up to 2,700x on complex benchmarks.

DaCe AD: A Unified, High-Performance Automatic Differentiation Framework for ML and Scientific Computing

Introduction and Motivation

Automatic differentiation (AD) is foundational for both ML and scientific computing, enabling efficient and accurate gradient computation for complex programs. However, existing AD frameworks exhibit significant limitations: restricted language support, required code modifications, suboptimal performance on scientific workloads, and naive memory strategies for storing forward-pass intermediates. These constraints have forced domain experts to manually implement derivatives, impeding productivity and maintainability.

DaCe AD addresses these challenges by providing a general, high-performance AD engine that requires no code rewrites, supports multiple languages (Python, PyTorch, ONNX, Fortran), and introduces a novel ILP-based checkpointing algorithm for optimal store/recompute trade-offs under memory constraints. The framework is built atop the Stateful DataFlow multiGraph (SDFG) IR, which enables precise dataflow analysis and optimization.

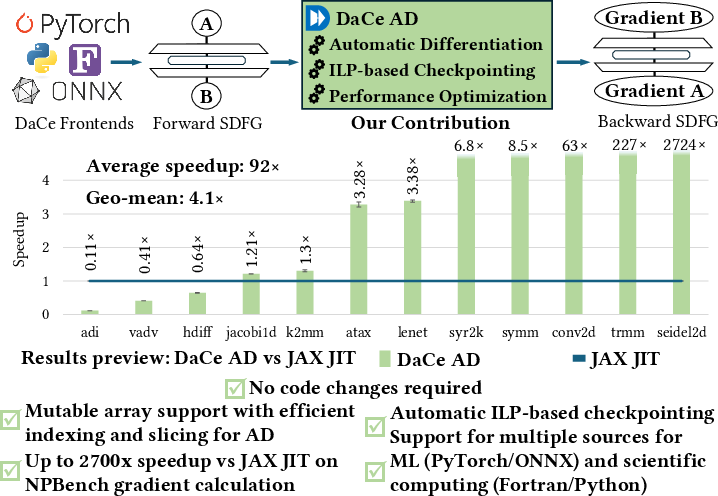
Figure 1: DaCe AD Contribution Overview.

SDFG-Based AD: Critical Computation Subgraph and Backward Pass Construction

DaCe AD leverages the SDFG IR to systematically construct the backward pass for gradient computation. The process centers on identifying the Critical Computation Subgraph (CCS)—the minimal subgraph containing all computations that contribute to the output with respect to the independent variables. This is achieved via a reverse breadth-first traversal from the output nodes, ensuring only necessary computations are included in the backward pass.

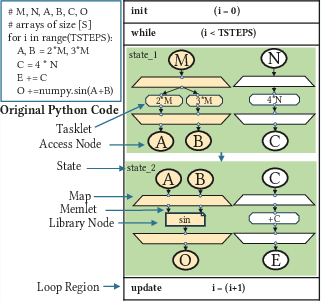
Figure 2: Example of an SDFG before optimization. Elements in yellow represent the CCS required for the backward pass.

For programs with control flow, the CCS may be over-approximated at compile time, but DaCe AD prunes unreachable states at runtime based on the actual execution path, ensuring correctness and efficiency.

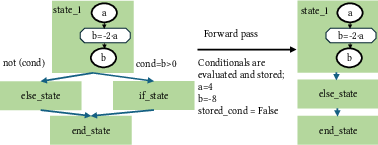
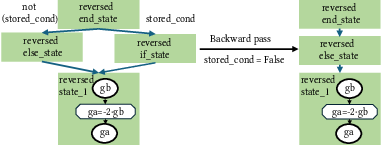
Figure 3: Forward pass evaluation stores results of conditional evaluations.

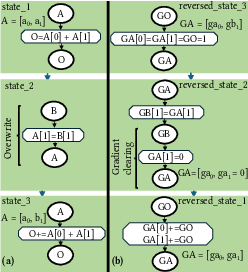
Figure 4: Example of gradient accumulation in the forward SDFG (a) and clearing in the backward SDFG (b).

Gradient accumulation is handled by initializing all gradient arrays to zero and accumulating contributions for arrays read multiple times in the forward pass. Overwrites are detected and handled by reinitializing the corresponding gradient indices, ensuring correctness in the presence of in-place updates.

Efficient Loop Differentiation: Sequential and Parallel Loops

Handling loops efficiently is a persistent challenge in AD. DaCe AD supports a broad class of loops, including parallel SDFG Maps and arbitrary nests of sequential for-loops with static iteration spaces. The framework classifies supported loop types and applies dataflow analysis to identify the CCS within loops, enabling compact backward pass generation without explicit unrolling.

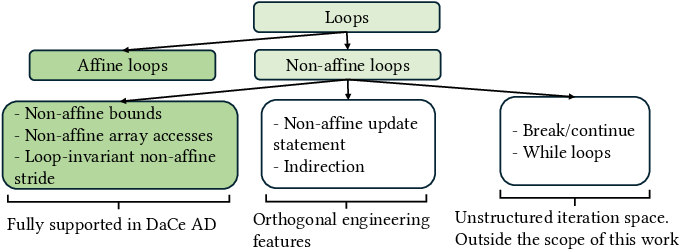
Figure 5: Taxonomy of loops for automatic differentiation.

Figure 6: CCS extraction and reversal for a loop. (a) Initial SDFG. (b) Unrolled loop. (c) CCS in yellow. (d) Rerolled loop. (e) Backward SDFG.

For parallel loops (Maps), DaCe AD generates a corresponding backward Map with reversed Tasklets and dataflow, ensuring efficient gradient propagation through parallel regions.

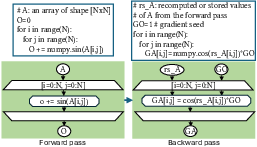
Figure 7: Example of automatic differentiation through parallel loops (SDFG Maps).

Store-Recompute Trade-Off: ILP-Based Checkpointing

A central challenge in reverse-mode AD is the re-materialization problem: deciding which forward-pass intermediates to store and which to recompute in the backward pass, balancing memory usage and computational cost. DaCe AD introduces an ILP-based algorithm that, given a user-specified memory constraint, determines the optimal store/recompute configuration to minimize total recomputation cost.

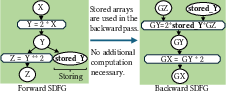
Figure 8: Storing arrays for the backward pass.

The ILP formulation models memory allocation/deallocation events and recomputation costs for each candidate array. Binary decision variables indicate whether to store or recompute each array, and constraints ensure that peak memory usage never exceeds the specified limit across all control-flow paths.

Implementation and Applicability

DaCe AD is implemented as an extension to DaCe and DaCeML, supporting Python, PyTorch, ONNX, and Fortran frontends. The framework requires no code modifications for AD compatibility, in contrast to JAX and other frameworks that impose array immutability and require extensive code rewrites for loops and in-place updates.

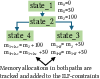
Figure 9: Python code.

Empirical Evaluation

DaCe AD is evaluated on NPBench, a suite of 52 high-performance computing benchmarks spanning ML, weather modeling, CFD, and quantum transport. After excluding benchmarks incompatible with AD, DaCe AD is compared to JAX JIT on 38 programs.

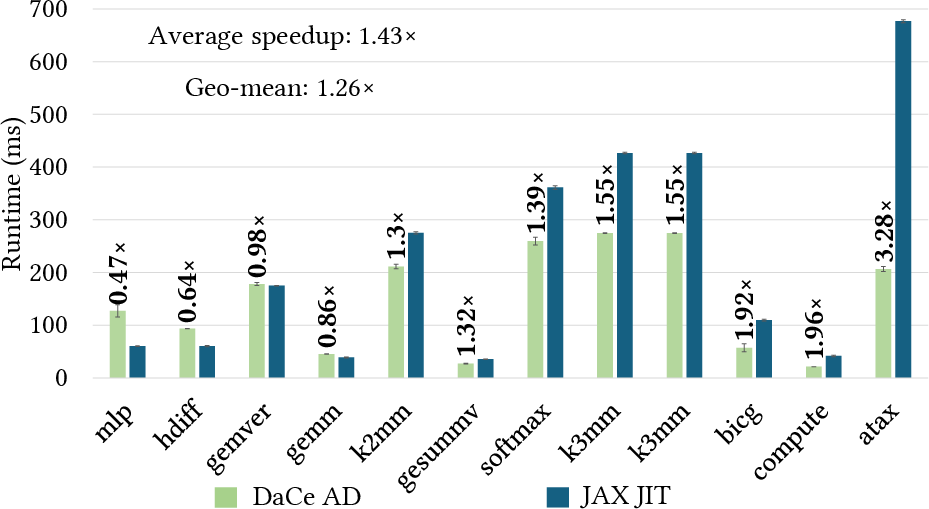
Figure 10: DaCe AD vs. JAX JIT: Performance on vectorized benchmarks. Data labels show DaCe AD speedup over JAX JIT.

On vectorized programs (matrix-matrix/vector operations), DaCe AD achieves an average speedup of 1.43x (geometric mean 1.27x) over JAX JIT, leveraging optimized library calls and efficient code generation.

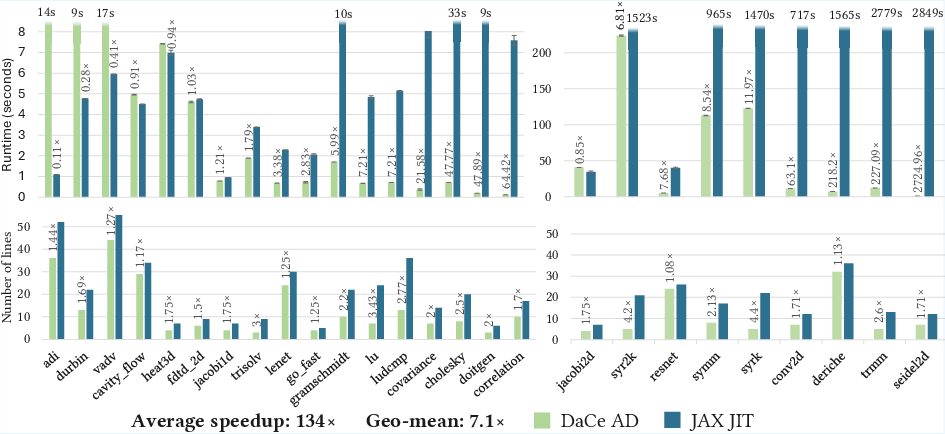
Figure 11: DaCe AD vs. JAX JIT - Non-vectorized benchmarks: performance and forward-pass program size.

On non-vectorized programs (with loops and control flow), DaCe AD outperforms JAX JIT on 20/26 benchmarks, with an average speedup of 134x (geometric mean 7.12x). The performance gap is attributed to JAX's array immutability, dynamic slicing overhead, and additional bound checks, all of which are avoided in DaCe AD via direct memory access and symbolic analysis.

Case Study: Seidel2d

A detailed analysis of the Seidel2d stencil kernel demonstrates DaCe AD's scalability. For large input sizes, DaCe AD is over 2,700x faster than JAX JIT, which suffers from excessive dynamic slicing and array creation overheads in the backward pass.

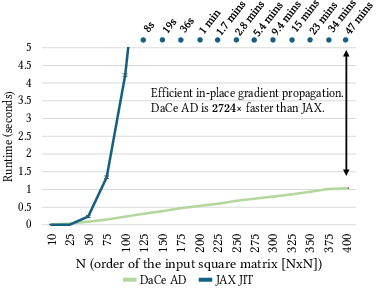
Figure 12: Variation of the size of the input 2D array for the Seidel2d benchmark.

ILP Checkpointing Evaluation

The ILP-based checkpointing strategy is validated on synthetic and real benchmarks. For a program with three candidate arrays, the ILP solver selects the configuration that stores the two most expensive arrays and recomputes the cheapest, achieving the fastest runtime under the memory constraint. The ILP solution time is negligible for practical problem sizes.

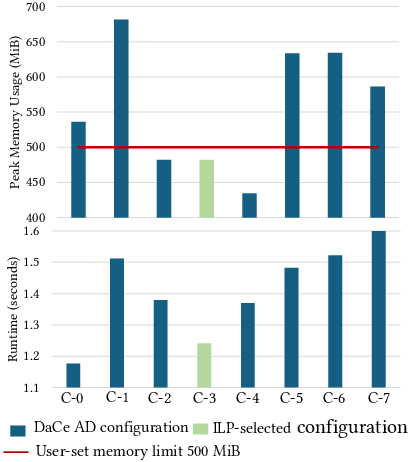
Figure 13: Performance and memory usage comparison of different store-recompute configurations.

GPU Performance

DaCe AD's algorithmic advantages persist on GPU. On an NVIDIA V100, DaCe AD outperforms JAX JIT on several benchmarks, with the performance gap narrowing but remaining significant due to the elimination of dynamic slicing and array immutability overheads.

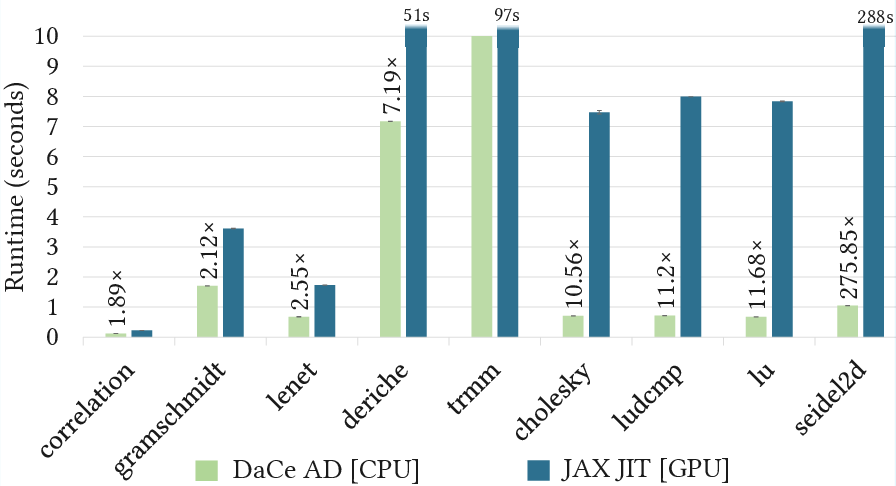
Figure 14: Performance results for DaCe AD [CPU: Intel Xeon Gold 6154] vs JAX JIT [GPU: NVIDIA V100].

Implications and Future Directions

DaCe AD demonstrates that a data-centric IR, combined with symbolic AD and ILP-based checkpointing, enables high-performance, general-purpose AD for both ML and scientific computing. The framework's ability to support multiple languages and code patterns without user intervention lowers the barrier for domain scientists to adopt AD in large-scale applications.

Theoretically, the approach generalizes to more complex control flow and could be extended to support recursion, indirections, and complex number operations. Practically, the ILP-based checkpointing strategy provides a principled, automatic solution to the re-materialization problem, which is critical for scaling AD to large scientific codes and hybrid AI4Science workflows.

Conclusion

DaCe AD unifies high-performance AD for ML and scientific computing, overcoming key limitations of existing frameworks. Its SDFG-based approach, efficient loop handling, and ILP-based checkpointing yield substantial performance gains—up to three orders of magnitude on real-world benchmarks—without requiring code rewrites. This work establishes a new standard for general, efficient, and user-friendly AD, with significant implications for the future of differentiable programming in both AI and scientific domains.