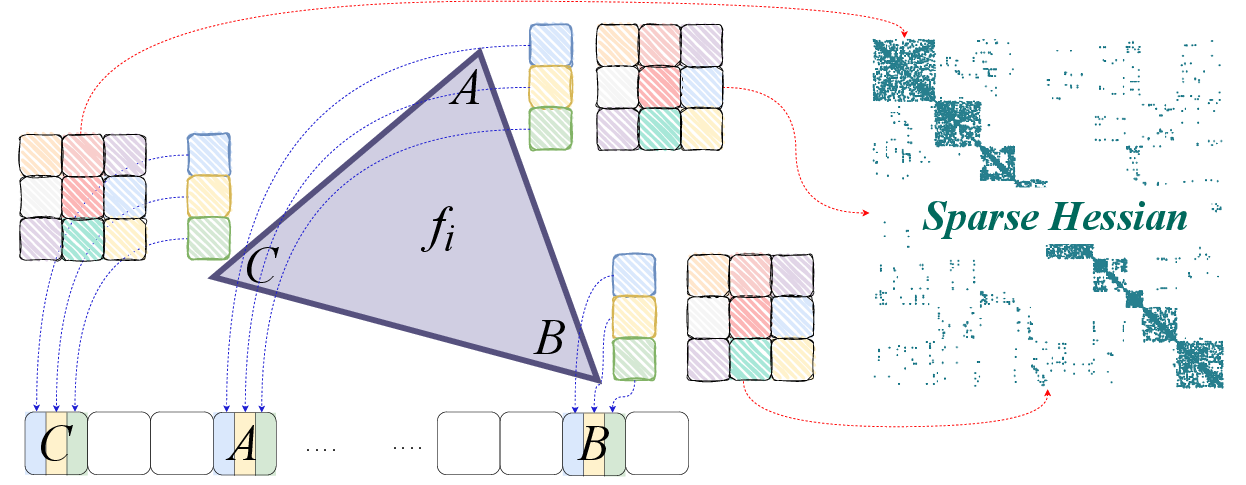
- The paper introduces a forward-mode AD system that leverages GPU registers and shared memory to exploit mesh sparsity and locality.
- It uses patch-based partitioning and operator overloading to optimize local derivative computations, achieving notable speedups in gradient and Hessian processing.
- Benchmark results on simulations like cloth deformation and mesh parameterization demonstrate performance improvements ranging from 2.76× to 7.28× over conventional AD frameworks.
Locality-Aware Automatic Differentiation on the GPU for Mesh-Based Computations
Introduction and Motivation
This work introduces a GPU-centric automatic differentiation (AD) system tailored for mesh-based computations, exploiting the inherent locality and sparsity of mesh energy functions. Unlike conventional AD frameworks optimized for dense tensor operations and reverse-mode differentiation, this system leverages forward-mode AD, confining all derivative calculations to GPU registers and shared memory. The approach is motivated by the observation that mesh-based problems—ubiquitous in simulation, geometry processing, and scientific computing—feature shallow, sparsely connected computation graphs, making forward-mode AD more efficient for GPU execution.
Figure 1: Fast and flexible AD for mesh-based functions via locality-aware forward-mode AD on the GPU, outperforming state-of-the-art AD frameworks in gradient, Hessian, and Hessian-vector product computations.
AD is essential for optimization-driven tasks in mesh-based applications, but existing frameworks (PyTorch, JAX, Warp, Dr.JIT) are designed for dense, global computation graphs typical of machine learning workloads. These frameworks fail to exploit mesh sparsity, resulting in poor runtime and excessive memory usage. Prior mesh-specific AD tools either run on the CPU (TinyAD), lack higher-order derivatives (Opt, Thallo, Warp), or focus on symbolic simplification (Herholz et al.). The presented system builds on the mesh-centric, element-wise differentiation paradigm but is explicitly designed for GPU execution, optimizing for memory locality and parallel throughput.

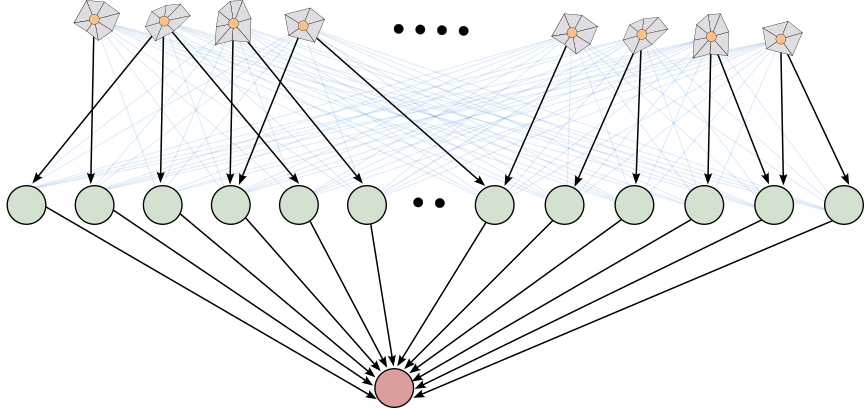
Figure 2: Dense connectivity in neural networks favors reverse-mode AD (left), while mesh-based problems yield sparse, local computation graphs where forward-mode AD is more efficient (right).
System Architecture and Programming Model
Programming Model
The user defines local energy terms over mesh elements (vertices, edges, faces) using a declarative interface. The system automatically applies these terms in parallel across the mesh, handling derivative tracking, memory management, and parallel execution. Active variables (subject to differentiation) and passive variables (constants) are mixed freely, and the system assembles global objective, gradient, and sparse Hessian structures from local contributions.
Internal Design
Cloth Simulation (Mass-Spring Model)
The system is benchmarked on classical mass-spring cloth simulation, where each mesh edge acts as a spring. The energy function combines inertial, elastic, and gravitational terms, optimized via Newton's method. Compared to PyTorch (reverse-mode, dense Hessians) and IndexedSum (sparse Hessian assembly), the presented system achieves 6.2× speedup over IndexedSum and is orders of magnitude faster than PyTorch, which suffers from out-of-memory errors on large meshes.
Mesh Parameterization (Symmetric Dirichlet Energy)
For mesh parameterization, the system minimizes face-based distortion using the symmetric Dirichlet energy. The optimization is performed using Newton's method with matrix-free conjugate gradient, relying on Hessian-vector products. Compared to PyTorch's double backward mechanism, the system achieves a geometric mean 2.76× speedup across mesh resolutions.

Figure 4: Symmetric Dirichlet energy minimization for mesh parameterization, showing progressive reduction in distortion and efficient matrix-free optimization.
Manifold Optimization
Spherical parameterization of genus-0 meshes is implemented, combining a barrier function for injectivity and a stretch penalty. Optimization is performed in the tangent space of the sphere using L-BFGS. The system achieves 1.78–1.87× speedup over JAXopt, with differentiation remaining the dominant cost.
Figure 5: Spherical parameterization of a genus-0 mesh, showing input, initial mapping, intermediate optimization, and final parameterization with distortion/injectivity visualization.
Laplacian Smoothing
Gradient computation for Laplacian smoothing is benchmarked against PyTorch, JAX, Warp, Dr.JIT, TinyAD, and a manual baseline. The system delivers 7.28× over PyTorch, 6.38× over Warp, 2.89× over JAX, and 1.98× over Dr.JIT, with negligible overhead compared to manual implementation. Atomic scatter for gradient accumulation is validated as efficient due to low write conflicts.
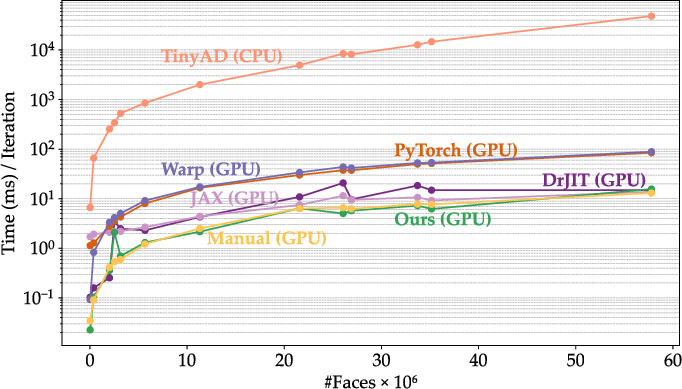
Figure 6: Scaling performance of the system versus GPU/CPU frameworks on Laplacian smoothing, demonstrating superior gradient computation throughput.
Implementation Considerations
- Computational Requirements: The system is designed for NVIDIA GPUs, leveraging CUDA and shared memory. Memory usage is minimized by confining local computations to registers/shared memory and preallocating global structures.
- Limitations: The current design enforces strict locality (immediate neighbors) to predict Hessian sparsity. Wider support (e.g., k-ring neighborhoods) and tetrahedral meshes are not yet supported.
- Deployment: The system is suitable for large-scale mesh-based optimization, simulation, and geometry processing tasks where high throughput and memory efficiency are critical.
Implications and Future Directions
The presented locality-aware AD system demonstrates that mesh-based differentiation is fundamentally local and sparse, enabling substantial performance gains on GPU architectures. The approach shifts the bottleneck from differentiation to linear solvers, opening opportunities for further acceleration in mesh-based optimization pipelines. Future work includes support for tetrahedral meshes, relaxation of locality constraints for wider neighborhood operations, and integration with advanced linear algebra libraries (e.g., cuSPARSE, cuSOLVER).
Conclusion
This work establishes a new paradigm for automatic differentiation in mesh-based computations, aligning algorithmic structure with GPU memory hierarchy and exploiting problem sparsity. The system consistently outperforms state-of-the-art AD frameworks in gradient, Hessian, and Hessian-vector product computations across diverse applications. The locality-aware design is a significant step toward scalable, high-performance geometry processing and simulation on modern parallel hardware.