Quantum Physics using Weighted Model Counting (2508.21288v1)

Abstract: Weighted model counting (WMC) has proven effective at a range of tasks within computer science, physics, and beyond. However, existing approaches for using WMC in quantum physics only target specific problem instances, lacking a general framework for expressing problems using WMC. This limits the reusability of these approaches in other applications and risks a lack of mathematical rigor on a per-instance basis. We present an approach for expressing linear algebraic problems, specifically those present in physics and quantum computing, as WMC instances. We do this by introducing a framework that converts Dirac notation to WMC problems. We build up this framework theoretically, using a type system and denotational semantics, and provide an implementation in Python. We demonstrate the effectiveness of our framework in calculating the partition functions of several physical models: The transverse-field Ising model (quantum) and the Potts model (classical). The results suggest that heuristics developed in automated reasoning can be systematically applied to a wide class of problems in quantum physics through our framework.

• The paper presents a framework that reduces quantum linear algebra problems into weighted model counting instances, enabling symbolic representation of complex matrix operations.
• The methodology employs a formal language based on Dirac notation to encode operations like matrix multiplication, trace, and the Kronecker product with proven correctness.
• Empirical results on Ising, TFIM, and Potts models demonstrate the framework’s potential for efficient, scalable computation in large-scale quantum systems.

Weighted Model Counting as a General Framework for Quantum Physics

Introduction and Motivation

The paper "Quantum Physics using Weighted Model Counting" (2508.21288) introduces a formal and practical framework for expressing linear algebraic problems in quantum physics as instances of weighted model counting (WMC). The central insight is that a broad class of quantum and classical physics computations—especially those involving partition functions and operator traces—can be systematically reduced to WMC problems, leveraging advances in automated reasoning and model counting solvers. This approach generalizes previous ad hoc reductions and provides a reusable, mathematically rigorous pipeline for encoding Dirac notation and matrix operations as Boolean formulas with associated weight functions.

Figure 1: Workflow of solving physics problems using our framework.

Formal Language and Matrix Representation

The core technical contribution is a formal language for representing scalars and $q^n \times q^m$ matrices, parameterized by a base $q$ (supporting both qubits and qudits). Expressions in this language are constructed from Dirac notation (bras and kets), matrix operations (addition, multiplication, Kronecker product, trace, transpose), and field endomorphisms. Each matrix or scalar is associated with a tuple $(\phi, W, x, y, q)$, where $\phi$ is a Boolean formula, $W$ a weight function, $x$ and $y$ are input/output variable encodings, and $q$ is the base.

The semantics are defined at two levels:

• Value semantics: The concrete matrix or scalar value.
• Representation semantics: The equivalence class of WMC representations that yield the same value.

The framework provides inductive rules for constructing WMC representations of all supported operations, with correctness formally proven via denotational semantics.

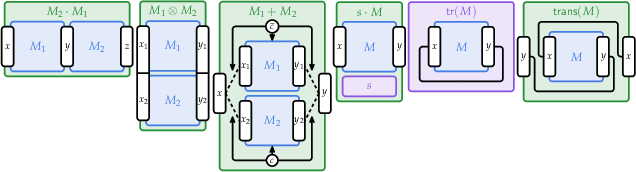
Figure 2: Diagram of multiplication operation on matrix representations.

Figure 3: Diagram of addition operation on matrix representations.

Figure 4: Diagram of Kronecker product operation on matrix representations.

Figure 5: Diagram of multiplying a matrix $M$ with a scalar $s$, using representations for both.

Figure 6: Diagram of the transpose of a matrix representation. Input and output variables are swapped.

Figure 7: Diagram of taking the trace of a matrix, using a matrix representation to get a scalar representation.

Implementation: DiracWMC

The authors provide a Python implementation, DiracWMC, which exposes the formal language as a user-facing API. Users can construct matrix expressions in Dirac notation, perform algebraic manipulations, and automatically obtain the corresponding WMC instance. The system supports multiple model counters (DPMC, Cachet, TensorOrder) and variable encodings (logarithmic, order, one-hot), allowing for empirical evaluation of encoding and solver choices.

The implementation demonstrates the ability to construct and evaluate extremely large matrices (e.g., $2^{100} \times 2^{100}$) symbolically, only invoking the model counter at the final evaluation step. This enables tractable computation of traces and selected entries for matrices that are otherwise infeasible to materialize explicitly.

Applications to Physical Models

Ising Model

The framework is applied to the classical Ising model, both reproducing the direct WMC encoding of Nagy et al. and providing a matrix-based encoding that generalizes to non-diagonal Hamiltonians. The equivalence of the two approaches is established, and empirical results show comparable performance across model counters.

Figure 8: Runtime of calculating the partition function of an $L \times L$ square lattice Ising model with interaction strengths and external field strengths from the standard normal distribution, averaged over five runs.

Transverse-Field Ising Model (TFIM)

For the quantum TFIM, the Hamiltonian includes non-commuting terms, necessitating Trotterization to approximate the exponential of the sum. The framework encodes the Trotterized product of exponentials and Hadamard gates as WMC instances, enabling computation of the quantum partition function for small systems. The performance degrades with increasing graph density due to reduced decomposition in the logical formula, but the approach is competitive with direct matrix exponential methods for sparse systems.

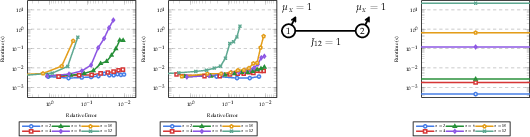
Figure 9: Runtime vs. relative error for TFIM partition function estimation using DPMC and Trotterization. Random graphs with Gaussian couplings, average degree 1.

Figure 10: Runtime of SciPy expm method for TFIM partition function. Uses same y-axis scale as Figure 9.

Potts Model

The framework is further extended to the $q$-state Potts model, supporting both the standard and generalized forms. The encoding leverages diagonal matrix representations and variable encodings for $q$-state variables. Empirical results show that for $q=3$, DPMC outperforms TensorOrder, but for $q=4$, TensorOrder scales better on larger instances, highlighting the impact of encoding and solver choice.

Figure 11: Runtime comparison of model counters on standard Potts models for $q=3$.

Figure 12: Encoding comparison on Potts partition computation using DPMC. Log encoding outperforms at higher $q$.

Theoretical and Practical Implications

The framework provides a unifying abstraction for expressing a wide range of quantum and classical physics computations as WMC problems. This enables the systematic application of advances in model counting, SAT solving, and symbolic reasoning to domains traditionally dominated by numerical linear algebra and tensor network methods. The approach is particularly advantageous when the problem structure allows for symbolic factorization and constraint sharing, enabling efficient parameter sweeps and reuse of compiled representations.

A notable limitation is the quadratic blow-up in formula size under repeated matrix addition, due to the introduction of control variables in the CNF encoding. The authors discuss potential alternative representations to mitigate this, as well as the possibility of extending the framework to higher-order tensors and categorical formulations.

Future Directions

Several avenues for further research are identified:

• Tensor extensions: Generalizing the framework to support higher-order tensors for many-body quantum systems.
• Alternative encodings: Developing more compact or solver-friendly representations, especially for operations that currently induce formula size blow-up.
• Categorical semantics: Reformulating the language in terms of monoidal categories to leverage compositionality and simplify correctness proofs.
• Max-WMC and optimization: Extending to maximum weighted model counting for ground-state and optimization problems.
• Solver integration: Closer coupling with model counter internals to exploit problem structure and improve scalability.

Conclusion

This work establishes a rigorous, extensible, and practical framework for encoding quantum and classical linear algebraic problems as weighted model counting instances. By bridging Dirac notation and WMC, it enables the application of automated reasoning tools to a broad class of physics computations, with demonstrated effectiveness on the Ising and Potts models and quantum partition functions. The approach generalizes prior work, supports arbitrary $q^n \times q^m$ matrices, and provides a foundation for future developments in symbolic and automated methods for quantum simulation and statistical physics.