FinCast: A Foundation Model for Financial Time-Series Forecasting (2508.19609v1)

Abstract: Financial time-series forecasting is critical for maintaining economic stability, guiding informed policymaking, and promoting sustainable investment practices. However, it remains challenging due to various underlying pattern shifts. These shifts arise primarily from three sources: temporal non-stationarity (distribution changes over time), multi-domain diversity (distinct patterns across financial domains such as stocks, commodities, and futures), and varying temporal resolutions (patterns differing across per-second, hourly, daily, or weekly indicators). While recent deep learning methods attempt to address these complexities, they frequently suffer from overfitting and typically require extensive domain-specific fine-tuning. To overcome these limitations, we introduce FinCast, the first foundation model specifically designed for financial time-series forecasting, trained on large-scale financial datasets. Remarkably, FinCast exhibits robust zero-shot performance, effectively capturing diverse patterns without domain-specific fine-tuning. Comprehensive empirical and qualitative evaluations demonstrate that FinCast surpasses existing state-of-the-art methods, highlighting its strong generalization capabilities.

• The paper presents FinCast, a billion-parameter, decoder-only transformer model that significantly reduces MSE and MAE over existing methods.
• The model incorporates innovative token-level sparse Mixture-of-Experts, learnable frequency embeddings, and a specialized PQ-loss to address non-stationary, multi-domain, and multi-resolution challenges.
• Empirical results demonstrate up to a 23% reduction in MSE, 16% reduction in MAE, and 5× faster inference, enabling robust real-time financial analytics.

FinCast: A Foundation Model for Financial Time-Series Forecasting

Introduction and Motivation

FinCast addresses the persistent challenges in financial time-series forecasting: temporal non-stationarity, multi-domain diversity, and multi-resolution heterogeneity. Existing models, including ARIMA, GARCH, RNNs, and even recent transformer-based architectures, exhibit limited generalization, overfitting, and require extensive domain-specific fine-tuning. FinCast is proposed as a billion-parameter, decoder-only transformer foundation model, trained on over 20 billion time points spanning diverse financial instruments and temporal resolutions. The model is designed to generalize robustly across domains and resolutions, supporting arbitrary context and forecast horizons at inference.

Model Architecture

FinCast’s architecture integrates three principal innovations: token-level sparse Mixture-of-Experts (MoE), learnable frequency embeddings, and a Point-Quantile (PQ) loss. The input tokenization block normalizes and patches raw time series, injects frequency embeddings, and projects to latent space. The decoder backbone applies causal self-attention and token-level sparse MoE routing, enabling expert specialization. The output block reverses normalization and produces both point and quantile forecasts.

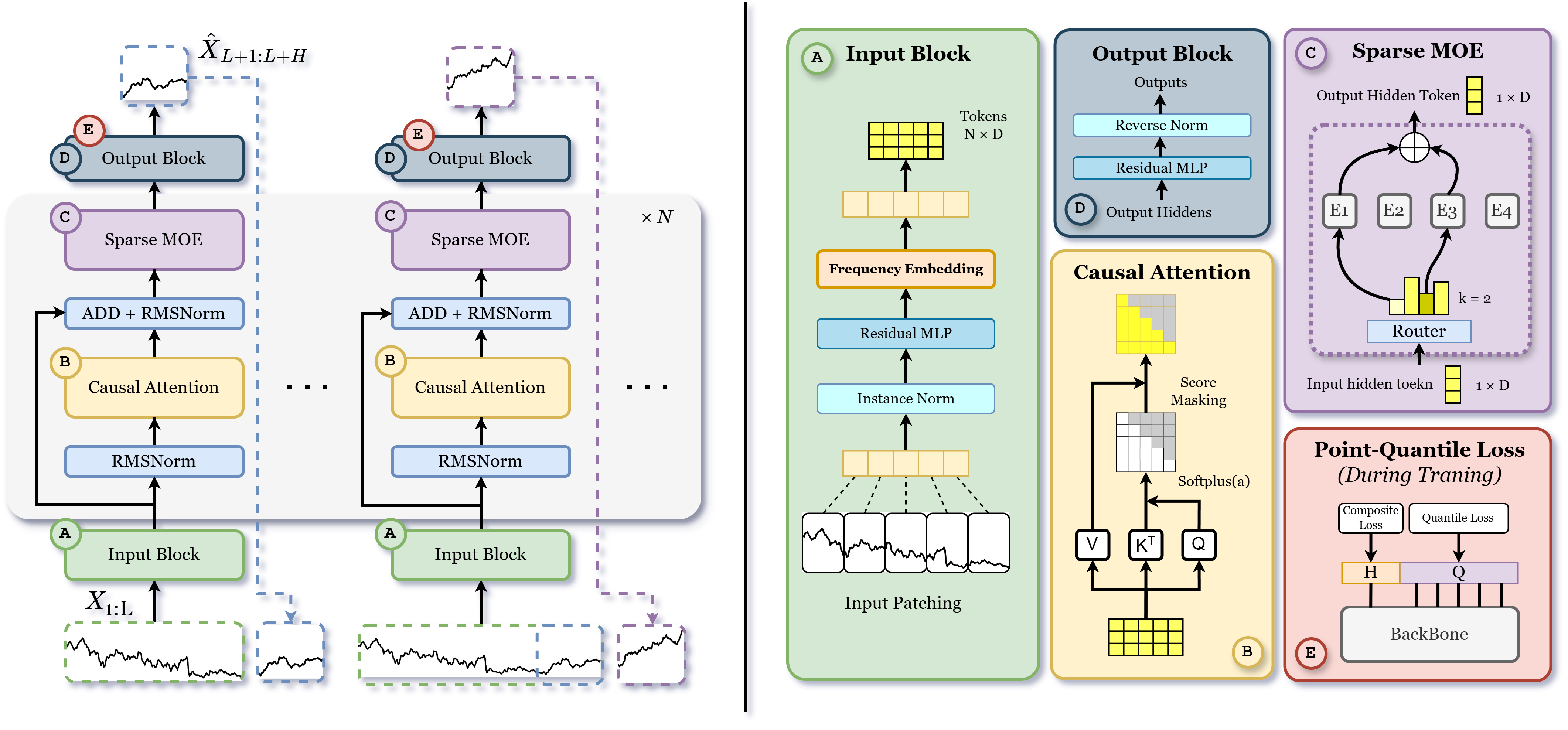
Figure 1: FinCast model architecture, illustrating input preprocessing, frequency embedding, causal attention, sparse MoE, output denormalization, and PQ-loss optimization.

Tokenization and Frequency Embedding

Instance normalization ensures scale invariance and lossless reversibility, critical for financial data with varying magnitudes. Learnable frequency embeddings encode temporal resolution, providing an explicit inductive bias for resolution-specific pattern learning. This mechanism is essential for generalization across minute, hourly, daily, and weekly data.

Sparse Mixture-of-Experts

The token-level sparse MoE layer routes each token to its top-$k$ experts, selected via a learned gating network. This design enables dynamic specialization, with experts capturing domain-specific characteristics such as volatility bursts, regime shifts, and seasonalities. Empirical ablation demonstrates that sparse MoE routing yields a 9.32% improvement in MSE over dense variants.

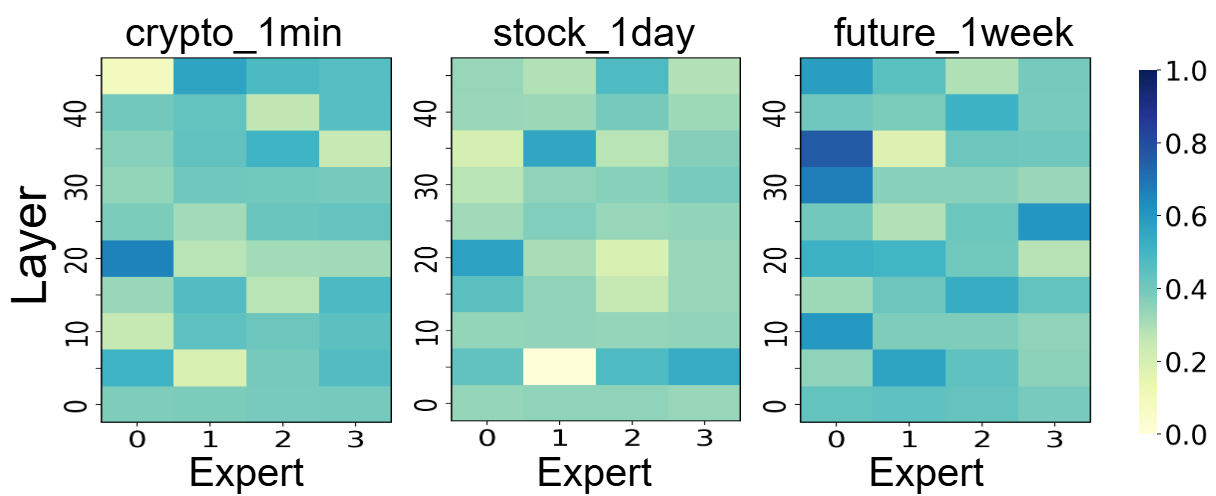
Figure 2: Expert activation patterns across datasets, showing domain-specific specialization of individual experts.

Output Block and PQ-Loss

The output block applies a residual MLP and inverse normalization, restoring the original scale. The PQ-loss combines Huber point loss, quantile loss, trend consistency, and MoE regularization. Quantile loss enforces distributional robustness, capturing forecast uncertainty and tail risks, while trend consistency aligns local dynamics. The PQ-loss is shown to prevent forecast collapse and mean reversion, outperforming MSE-only objectives by 7.62%.

Figure 3: Visualization of point and quantile outputs during training, demonstrating robust uncertainty modeling and avoidance of forecast collapse.

Training and Inference

FinCast is trained on a curated dataset of 2.4 million time series, including stocks, crypto, forex, futures, and macroeconomic indicators, with rigorous data cleaning. Training employs variable context lengths, patch-wise masking, AdamW optimization, and distributed data parallelism across 8 H200 GPUs. The model supports efficient autoregressive inference, generating forecasts in patch-wise segments, and is deployable on consumer-grade GPUs.

Empirical Evaluation

Zero-Shot and Supervised Benchmarks

FinCast is evaluated on strict zero-shot and supervised financial forecasting benchmarks. In zero-shot settings, it consistently outperforms TimesFM, Chronos-T5, and TimesMOE across all domains and horizons, achieving an average 20% reduction in MSE. In supervised settings, both zero-shot and fine-tuned variants surpass state-of-the-art models (PCIE, PatchTST, D-Va, Autoformer, Informer), with the zero-shot model alone reducing MSE by 23% and MAE by 16%. Fine-tuning further improves performance, with minimal adaptation required.

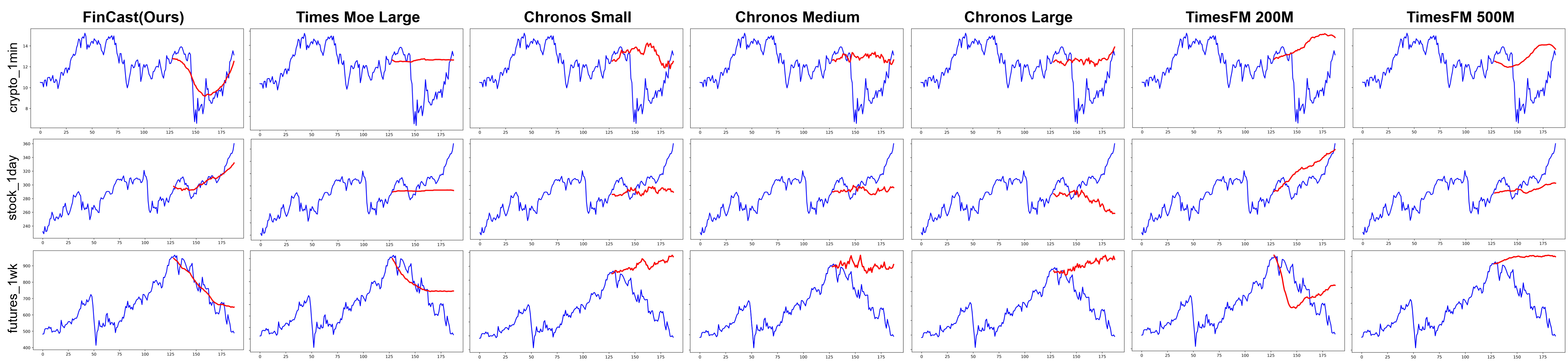
Figure 4: Zero-shot forecasting examples from the benchmark, illustrating FinCast’s trend sensitivity and adaptation to non-stationary patterns.

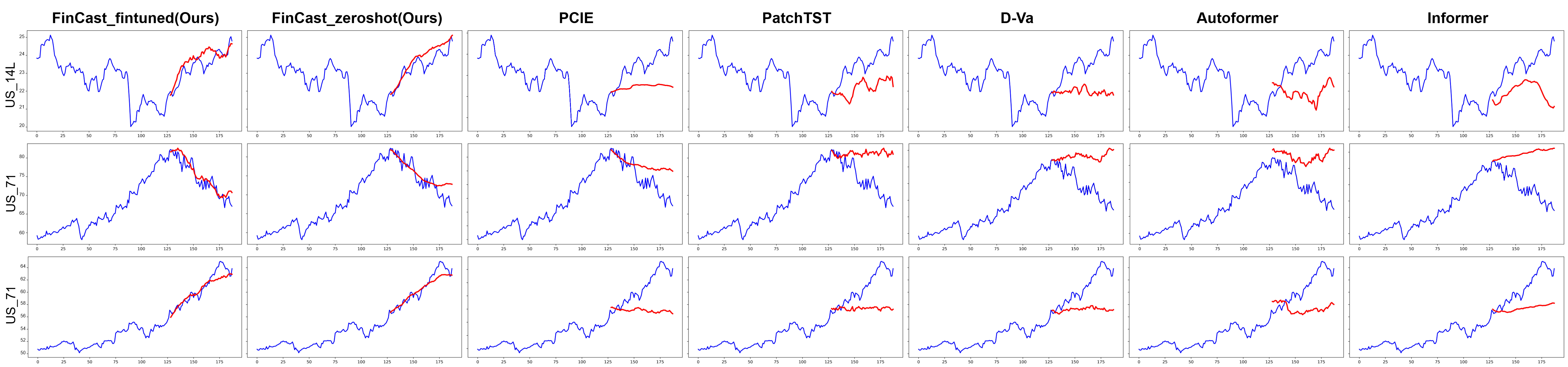
Figure 5: Supervised forecasting examples, highlighting FinCast’s ability to avoid mean reversion and flat-line outputs prevalent in baseline models.

Ablation and Qualitative Analysis

Ablation studies confirm the necessity of sparse MoE, PQ-loss, and frequency embeddings for robust generalization. Qualitative results demonstrate FinCast’s capacity to adapt to abrupt pattern shifts, domain transitions, and resolution changes, where baseline models regress to conservative outputs.

Inference Speed

FinCast achieves up to 5× faster inference than competing models, maintaining superior accuracy. This efficiency is attributed to conditional computation in sparse MoE and patch-wise tokenization, enabling practical deployment in latency-sensitive financial applications.

Figure 6: Inference speed versus performance, showing FinCast’s favorable trade-off frontier compared to other foundation models.

Implications and Future Directions

FinCast establishes a new paradigm for financial time-series modeling, demonstrating that large-scale, domain-specialized foundation models can generalize across non-stationary, multi-domain, and multi-resolution data without task-specific fine-tuning. The integration of sparse MoE, frequency embeddings, and PQ-loss is empirically validated as essential for robust performance. The model’s inference efficiency and adaptability make it suitable for real-time financial analytics, risk management, and automated trading.

Theoretically, FinCast’s architecture suggests that explicit conditioning on temporal resolution and dynamic expert specialization are critical for handling the idiosyncrasies of financial data. The PQ-loss framework provides a principled approach to uncertainty modeling, which is vital for risk-sensitive applications.

Future work should focus on scaling pretraining to larger, higher-quality datasets, exploring more granular expert routing, and extending the model to multi-modal financial data (e.g., textual news, order book depth). The open-source release of weights and code facilitates reproducibility and further research.

Conclusion

FinCast represents a significant advancement in financial time-series forecasting, integrating architectural and loss function innovations to achieve robust, generalizable, and efficient forecasting across diverse financial domains and temporal resolutions. The empirical results substantiate the model’s superiority over existing methods, both in zero-shot and supervised settings. The approach and findings have broad implications for the development of foundation models in finance and time-series analysis.