Communication Efficient LLM Pre-training with SparseLoCo (2508.15706v1)

Abstract: Communication-efficient distributed training algorithms have received considerable interest recently due to their benefits for training LLMs in bandwidth-constrained settings, such as across data centers and over the internet. Despite reducing communication frequency, these methods still typically require communicating a full copy of the model's gradients-resulting in a communication bottleneck even for cross-datacenter links. Furthermore, they can slightly degrade performance compared to a naive AdamW DDP baseline. While quantization and error feedback are often applied to reduce the pseudo-gradient's size, in the context of LLM pre-training, existing approaches have been unable to additionally leverage sparsification and have obtained limited quantization. In this work, we introduce SparseLoCo, a communication-efficient training algorithm for LLMs that effectively leverages Top-k sparsification and quantization to reach extreme compression ratios of up to 1-3% sparsity and 2-bit quantization while outperforming full-precision DiLoCo. Our key observations are that outer momentum can be locally approximated by an error feedback combined with aggressive sparsity and that sparse aggregation can actually improve model performance. We empirically demonstrate in a range of communication-constrained LLM training settings that SparseLoCo provides significant benefits in both performance and communication cost.

• The paper demonstrates that combining aggressive Top-k sparsification, 2-bit quantization, and local error feedback significantly reduces communication while preserving LLM pre-training quality.
• It introduces a multi-iteration distributed framework that outperforms existing methods like DiLoCo and DeMo across different communication intervals.
• Empirical results on a 512M-parameter model validate lower loss and optimal trade-offs between communication volume and performance.

Communication-Efficient LLM Pre-training with SparseLoCo

Introduction

The increasing scale of LLMs has made distributed pre-training across multiple data centers and over the internet a critical challenge, primarily due to the communication bottleneck associated with synchronizing model updates. While prior approaches such as DiLoCo and DeMo have addressed communication efficiency via reduced synchronization frequency and gradient compression, they have not fully exploited the potential of aggressive sparsification and quantization in the context of LLM pre-training. The paper introduces SparseLoCo, a method that unifies $Top$-$k$ sparsification, quantization, and error feedback within a multi-iteration distributed training framework, achieving extreme compression ratios (1–3% density, 2-bit quantization) while outperforming full-precision DiLoCo in both loss and communication cost.

Methodological Advances

SparseLoCo is motivated by the observation that the global outer momentum in DiLoCo can be effectively approximated by local error feedback accumulators, especially when combined with aggressive $Top$-$k$ sparsification. This insight enables the replacement of global momentum with local error feedback, allowing for highly compressed communication without sacrificing convergence or final model quality.

The algorithm operates as follows:

• Each worker performs $H$ local steps of an adaptive optimizer (e.g., AdamW), computes the pseudo-gradient as the difference between the pre- and post-local-update parameters, and updates a local error feedback buffer.
• The $Top$-$k$ entries of the error buffer are selected (optionally within tensor chunks), quantized (down to 2 bits), and communicated.
• The global update is computed as the average of the sparse, quantized pseudo-gradients, and applied to all workers.

This design enables both infrequent and highly compressed communication, with the error feedback mechanism compensating for information loss due to sparsification and quantization.

Empirical Results

SparseLoCo is evaluated on a 512M-parameter LLaMA-style transformer using the DCLM dataset, with strong baselines including DiLoCo, DeMo, and AdamW DDP. The experiments systematically vary the communication interval $H$ and the sparsity level $k$, and include ablations on quantization, chunking, and error feedback design.

SparseLoCo consistently outperforms DiLoCo and DeMo across a range of communication intervals ($H \in \{15, 30, 50, 100\}$), achieving lower final loss while communicating orders of magnitude less data.

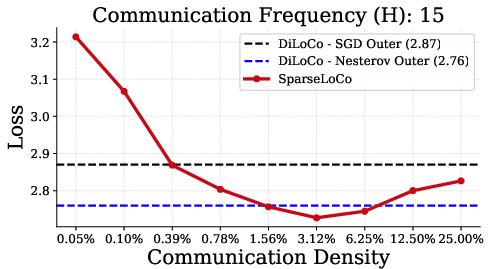
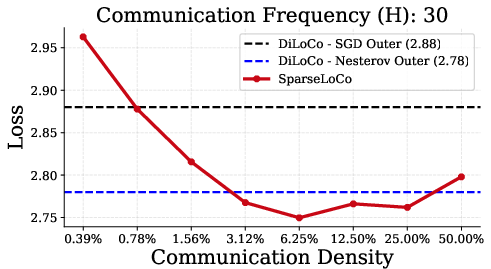
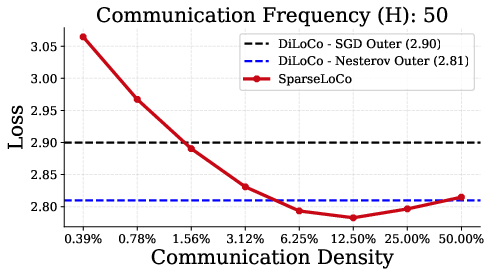
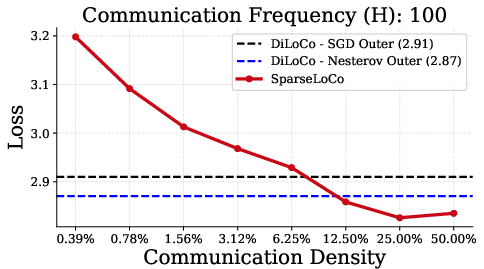
Figure 1: SparseLoCo outperforms DiLoCo for $H \in \{15, 30, 50, 100\}$ communication steps, with optimal sparsity increasing as $H$ increases.

SparseLoCo is also shown to lie on the Pareto frontier of loss versus communication volume, outperforming all baselines in both ring all-gather and parameter server topologies.

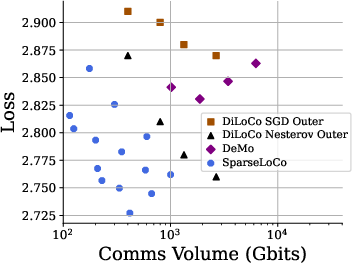
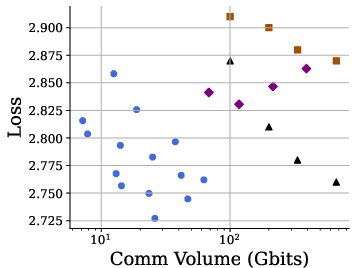
Figure 2: SparseLoCo achieves the best trade-off between loss and communication volume across both ring and parameter server communication topologies.

Key empirical findings include:

• SparseLoCo achieves lower loss than DiLoCo and DeMo at equivalent or lower communication budgets.
• 2-bit quantization incurs negligible degradation in loss compared to full precision.
• Sparse aggregation (via $Top$-$k$) can improve performance over dense aggregation, contradicting the intuition that sparsification is always detrimental.
• The optimal sparsity increases with the number of local steps $H$, reflecting the increased support of the aggregated pseudo-gradient.
• Naively combining global outer momentum with error feedback degrades performance at high sparsity, supporting the design choice of local error feedback only.
• Random-$k$ sparsification is significantly inferior to $Top$-$k$, emphasizing the importance of selecting high-magnitude updates.

Design Choices and Ablations

The paper provides a comprehensive set of ablations to justify the design of SparseLoCo:

• Error Feedback vs. Outer Momentum: Local error feedback is sufficient and preferable to global outer momentum when aggressive sparsification is used.
• $Top$-$k$ vs. Random-$k$: $Top$-$k$ selection is critical for maintaining performance under sparsification.
• Quantization: 2-bit quantization is supported without additional accumulators, and does not degrade performance.
• Chunking: Applying $Top$-$k$ within tensor chunks reduces index transmission overhead and can improve performance, especially in the single-step setting.

Practical Implications and Deployment

SparseLoCo is particularly well-suited for globally distributed, bandwidth-constrained training environments, such as cross-datacenter or internet-scale collaborative training. The method has been deployed in real-world settings (e.g., Bittensor/Templar), demonstrating practical communication times (e.g., 12 seconds for 8B models, 70 seconds for 70B models with 20 peers) that are negligible compared to compute time, even over commodity internet connections.

The algorithm is compatible with both all-reduce and all-gather communication primitives, and can be integrated as a drop-in replacement for DiLoCo in existing distributed training frameworks. The use of chunked $Top$-$k$ and custom index compression further reduces communication overhead.

Theoretical and Future Directions

The results suggest that sparse aggregation, when combined with error feedback, not only preserves but can enhance the convergence and generalization of multi-iteration distributed training. This challenges the conventional wisdom that dense aggregation is always optimal and opens new avenues for research on the role of sparsity in distributed optimization.

Future work may explore:

• Theoretical analysis of the interplay between error feedback, sparsification, and adaptive optimization in the multi-iteration regime.
• Extensions to heterogeneous data and federated learning settings.
• Further optimizations in index compression and communication protocols.
• Application to even larger models and more diverse hardware/network environments.

Conclusion

SparseLoCo demonstrates that aggressive $Top$-$k$ sparsification and quantization, when combined with local error feedback, enable highly communication-efficient LLM pre-training without sacrificing—and in some cases improving—model quality. The method achieves state-of-the-art trade-offs between loss and communication volume, is robust across a range of hyperparameters and deployment scenarios, and is immediately applicable to real-world distributed training of large models. These findings have significant implications for the scalability and democratization of LLM pre-training, particularly in bandwidth-constrained and globally distributed environments.