Depth-Breadth Synergy in RLVR: Unlocking LLM Reasoning Gains with Adaptive Exploration (2508.13755v1)

Abstract: Reinforcement Learning with Verifiable Reward (RLVR) has emerged as a powerful paradigm for unlocking reasoning capabilities in LLMs, yet its full potential is hindered by two under-explored dimensions: Depth-the hardest problem a model can sample; Breadth-the number of instances consumed in a single iteration. We dissect the popular GRPO algorithm and reveal a systematic bias: the cumulative-advantage disproportionately weights samples with medium accuracy, while down-weighting the low-accuracy instances that are crucial for pushing reasoning boundaries. To rectify the depth neglect, we introduce Difficulty Adaptive Rollout Sampling (DARS), which re-weights hard problems through targeted multi-stage rollouts, thereby increasing the number of positive rollouts for hard problems. Empirically, naively enlarging rollout size only accelerates convergence and even hurts Pass@K. Our DARS, in contrast, delivers consistent Pass@K gains without extra inference cost at convergence. Just as we adaptively expanded the depth of exploration, we now ask whether aggressively scaling the breadth of training data can further amplify reasoning gains. To this end, we intensely scale batch size and replace PPO's mini-batch iterations with full-batch updates over multiple epochs. Increasing breadth significantly enhances Pass@1 performance. Large-breadth training sustains high token-level entropy, indicating continued exploration and reduced gradient noise. We further present DARS-B, which augments DARS with large breadth, and demonstrate simultaneous gains in Pass@K and Pass@1. The results confirm that breadth and adaptive exploration across depth operate as orthogonal dimensions in RLVR, which are key to unleashing the reasoning power of RLVR.

• The paper identifies a bias in standard RLVR methods that underutilizes high-difficulty problems, limiting the model's reasoning capacities.
• It introduces DARS, an adaptive rollout sampling approach that reallocates extra rollouts to hard problems, thereby improving Pass@K without sacrificing Pass@1.
• DARS-B synergistically integrates full-batch updates with breadth scaling, achieving superior performance on both Pass@1 and Pass@K across various model scales.

Depth-Breadth Synergy in RLVR: Unlocking LLM Reasoning Gains with Adaptive Exploration

Introduction

This paper presents a systematic analysis and novel methodology for enhancing the reasoning capabilities of LLMs via Reinforcement Learning with Verifiable Reward (RLVR). The authors identify two critical, under-explored dimensions in RLVR optimization: Depth (the hardest problems a model can learn to solve) and Breadth (the number of instances processed per training iteration). The work reveals a fundamental bias in the widely adopted GRPO algorithm, which limits the model's ability to learn from high-difficulty problems, thereby capping Pass@K performance. To address this, the paper introduces Difficulty Adaptive Rollout Sampling (DARS) and its breadth-augmented variant DARS-B, demonstrating that depth and breadth are orthogonal and synergistic axes for RLVR optimization.

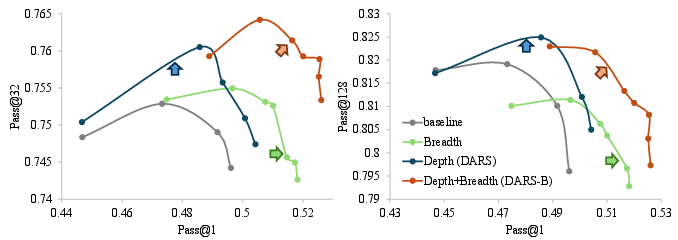
Figure 1: Training dynamics of Pass@1 and Pass@K performance. DARS significantly improves Pass@K and is complementary to breadth scaling for Pass@1.

Depth and Breadth in RLVR: Empirical Analysis

Depth: Hardest Problem Sampled

Depth is defined as the hardest problem that can be correctly answered during RLVR training. The analysis shows that simply increasing rollout size does not consistently improve Pass@K and may even degrade it for smaller models. The GRPO algorithm's cumulative advantage calculation is shown to disproportionately favor medium-difficulty problems, neglecting high-difficulty instances that are essential for expanding the model's reasoning capacity.

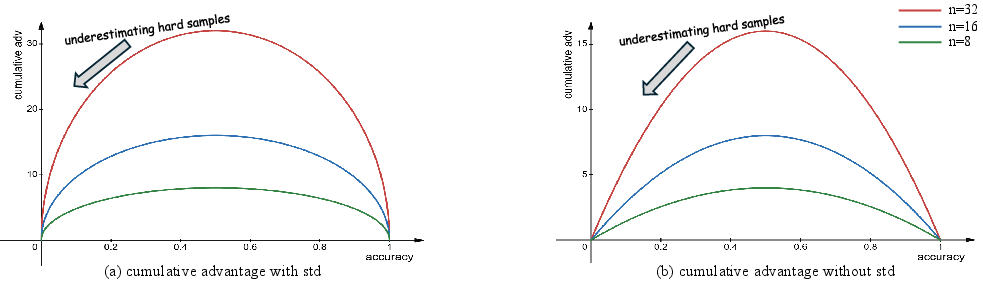
Figure 2: Statistical results of cumulative advantage. Both advantage calculation methods underestimate high-difficulty problems.

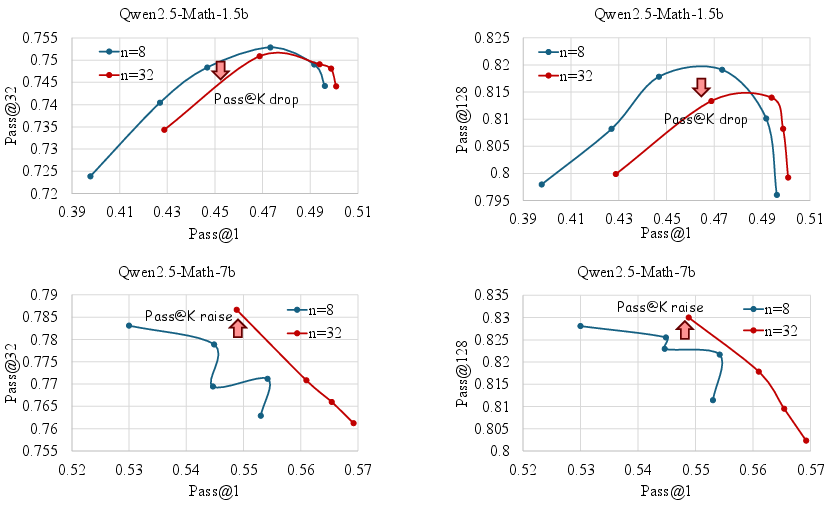
Figure 3: Training dynamics of Pass@1 and Pass@K for Qwen2.5-Math-1.5b and Qwen2.5-Math-7b with different rollout sizes.

Breadth: Iteration Instance Quantity

Breadth refers to the number of instances processed per RLVR iteration. Increasing batch size (breadth) leads to significant improvements in Pass@1 across all model scales, attributed to more accurate gradient estimation and reduced noise. However, excessive breadth can harm Pass@K for smaller models, indicating a trade-off.

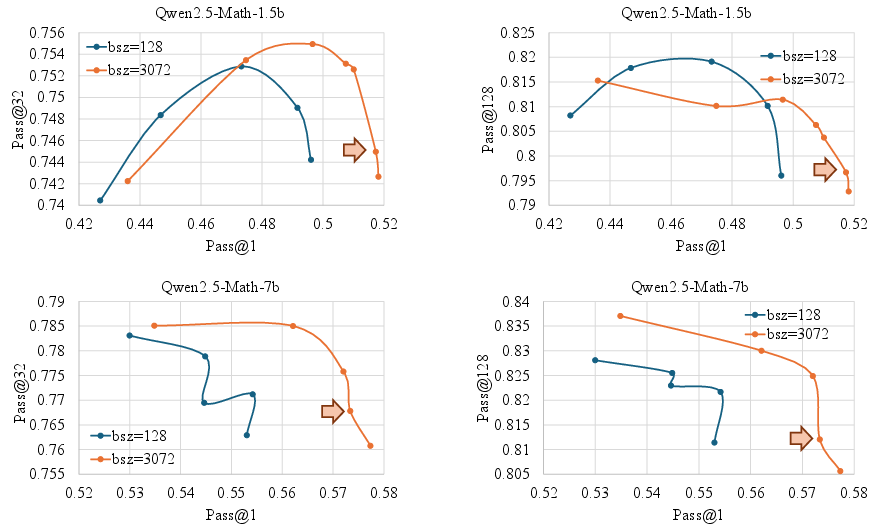
Figure 4: Training dynamics of Pass@1 and Pass@K for Qwen2.5-Math-1.5b and Qwen2.5-Math-7b with different batch sizes.

Breadth also sustains higher token entropy, which is correlated with stronger exploration capabilities and delayed premature convergence.

Figure 5: Training dynamics of Pass@1 and token entropy for Qwen2.5-Math-1.5b and Qwen2.5-Math-7b.

Methodology: DARS and DARS-B

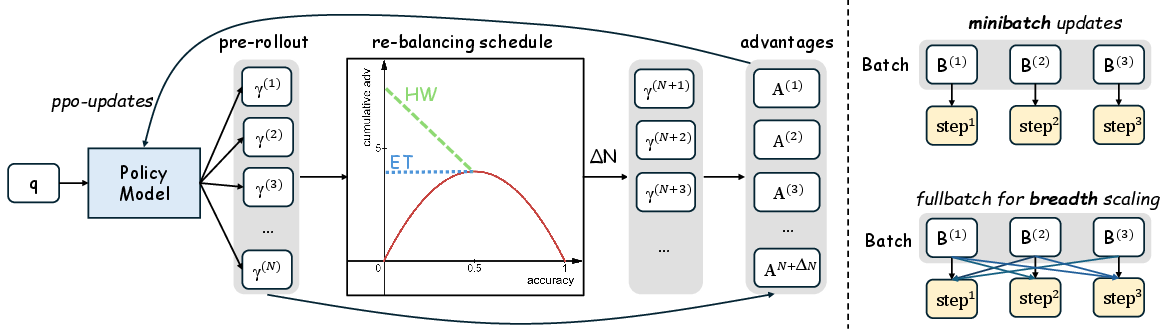
Difficulty Adaptive Rollout Sampling (DARS)

DARS operates in two phases:

1. Pre-Rollout Difficulty Estimation: For each question, a lightweight rollout estimates empirical accuracy, assigning a difficulty score as the complement of accuracy.
2. Multi-Stage Rollout Re-Balancing: Additional rollouts are allocated to low-accuracy (hard) problems, rebalancing the cumulative advantage to up-weight difficult samples.

Two re-balancing schedules are proposed:

• Equal-Treatment (ET): Raises the cumulative advantage of all problems below a threshold to that of medium-difficulty problems.
• Hardness-Weighted (HW): Allocates more rollouts to lower-accuracy problems in a monotonic fashion.

  Figure 6: The overall training framework of DARS with breadth scaling. DARS consists of difficulty estimation and re-balancing phases; breadth scaling replaces PPO minibatch with full-batch updates.

Depth-Breadth Synergy: DARS-B

DARS-B integrates DARS with large-breadth training by replacing PPO mini-batch updates with full-batch gradient descent across multiple epochs. This enables dynamic batch-size adjustments and maximizes training breadth, eliminating gradient noise and sustaining exploration. DARS-B achieves simultaneous improvements in Pass@1 and Pass@K, confirming the orthogonality and synergy of depth and breadth in RLVR.

Experimental Results

The authors conduct extensive experiments on Qwen2.5-Math-1.5b and Qwen2.5-Math-7b models using five mathematical reasoning benchmarks. Key findings include:

• Breadth scaling consistently improves Pass@1, with Breadth-Naive outperforming both GRPO baseline and Depth-Naive.
• DARS-B achieves the highest Pass@1 and matches or exceeds the best Pass@K scores, demonstrating the complementary strengths of depth and breadth.
• DARS delivers higher Pass@K at any fixed Pass@1 level compared to naive rollout scaling, with improved training efficiency by targeting hard problems.

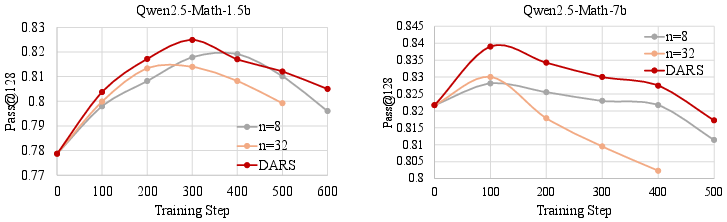
  Figure 7: Training dynamics of Pass@128 performance with different training steps for Qwen2.5-Math-1.5b and Qwen2.5-Math-7b.

  

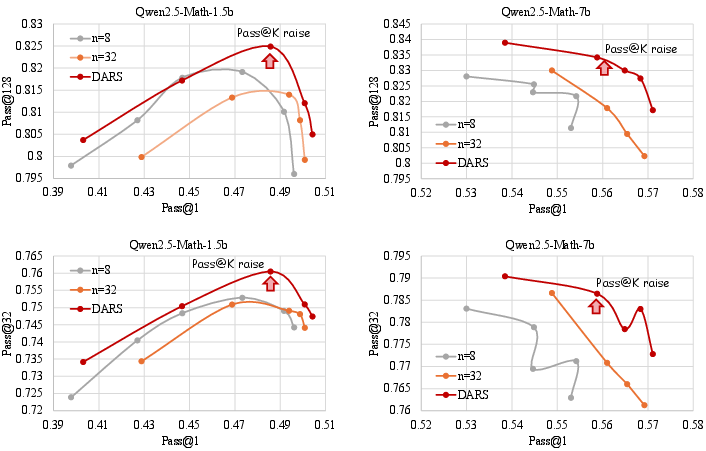
  Figure 8: Training dynamics of Pass@32/Pass@128 and Pass@1 performance with different training steps for Qwen2.5-Math-1.5b and Qwen2.5-Math-7b.

  

  Figure 9: Complementary improvement of Depth and Breadth Synergy for Pass@1 and Pass@K (K=32/128) performance.

Theoretical and Practical Implications

The work provides a rigorous diagnosis of the limitations in current RLVR algorithms, particularly the depth bias in cumulative advantage computation. By introducing DARS and DARS-B, the authors offer a principled approach to rebalancing exploration and exploitation in RLVR, enabling LLMs to learn from harder problems without sacrificing single-shot performance. The synergy between depth and breadth is empirically validated, suggesting that future RLVR pipelines should jointly optimize both dimensions.

Practically, the proposed methods are computationally efficient, as DARS targets additional rollouts only to hard problems, and DARS-B leverages full-batch updates for maximal gradient accuracy and exploration. The framework is compatible with existing RLVR pipelines and can be readily integrated into large-scale LLM training.

Future Directions

Potential avenues for future research include:

• Extending DARS-B to larger model scales and diverse reasoning domains (e.g., code synthesis, scientific reasoning).
• Investigating adaptive schedules for rollout allocation and batch size scaling.
• Exploring the interaction between RLVR and other self-improvement mechanisms, such as self-reflection and curriculum learning.
• Analyzing the long-term effects of depth-breadth synergy on model generalization and robustness.

Conclusion

This paper identifies and addresses a critical bottleneck in RLVR for LLM reasoning: the neglect of hard problems due to cumulative advantage bias. By introducing Difficulty Adaptive Rollout Sampling (DARS) and its breadth-augmented variant DARS-B, the authors demonstrate that depth and breadth are orthogonal, synergistic dimensions for RLVR optimization. The proposed methods yield simultaneous improvements in Pass@1 and Pass@K, providing a robust framework for advancing LLM reasoning capabilities. The findings have significant implications for the design of future RLVR algorithms and the development of more capable, self-improving LLMs.