Plane Detection and Ranking via Model Information Optimization (2508.09625v1)

Abstract: Plane detection from depth images is a crucial subtask with broad robotic applications, often accomplished by iterative methods such as Random Sample Consensus (RANSAC). While RANSAC is a robust strategy with strong probabilistic guarantees, the ambiguity of its inlier threshold criterion makes it susceptible to false positive plane detections. This issue is particularly prevalent in complex real-world scenes, where the true number of planes is unknown and multiple planes coexist. In this paper, we aim to address this limitation by proposing a generalised framework for plane detection based on model information optimization. Building on previous works, we treat the observed depth readings as discrete random variables, with their probability distributions constrained by the ground truth planes. Various models containing different candidate plane constraints are then generated through repeated random sub-sampling to explain our observations. By incorporating the physics and noise model of the depth sensor, we can calculate the information for each model, and the model with the least information is accepted as the most likely ground truth. This information optimization process serves as an objective mechanism for determining the true number of planes and preventing false positive detections. Additionally, the quality of each detected plane can be ranked by summing the information reduction of inlier points for each plane. We validate these properties through experiments with synthetic data and find that our algorithm estimates plane parameters more accurately compared to the default Open3D RANSAC plane segmentation. Furthermore, we accelerate our algorithm by partitioning the depth map using neural network segmentation, which enhances its ability to generate more realistic plane parameters in real-world data.

• The paper presents a novel information-theoretic framework for objectively detecting and ranking planes from depth images, reducing false positives.
• It integrates discrete depth data and sensor noise models into model selection, outperforming traditional RANSAC and neural network methods.
• Experiments on synthetic and real-world datasets validate the approach, demonstrating improved segmentation quality for robotics and mapping.

Plane Detection and Ranking via Model Information Optimization

Introduction

This paper presents a principled framework for plane detection in depth images, addressing the limitations of conventional RANSAC-based approaches. The authors propose an information-theoretic model selection criterion that leverages the discrete nature of depth sensor data and incorporates sensor physics and noise models. The method aims to objectively determine the true number of planes in a scene, prevent false positives, and provide a ranking of detected planes based on their information reduction. The approach is validated on both synthetic and real-world datasets, demonstrating improved accuracy and robustness compared to standard RANSAC and neural network-based methods.

Figure 1: RGB image of a scene used for plane detection evaluation.

Background and Motivation

Plane detection is a fundamental task in robotics and computer vision, with applications in navigation, mapping, and scene understanding. Traditional methods such as RANSAC offer probabilistic guarantees but suffer from ambiguous inlier threshold selection, slow convergence in complex scenes, and susceptibility to false positives when the true number of planes is unknown. Deep learning methods, while promising, are limited by the quality of ground truth data and often rely on RGB inputs, which may not capture geometric constraints effectively.

The proposed framework builds on the information-theoretic approach of Yang and Förstner, extending it by integrating sensor noise models and assignment mask penalties to prevent overfitting. The method treats each depth observation as a discrete random variable, and candidate plane models are generated via random sub-sampling. The model with the minimum information is selected as the most likely ground truth, and the information reduction metric is used to rank plane quality.

Mathematical Formulation

Let $X$ be a set of $k$ points in $\mathbb{R}^n$, each lying on discrete intervals determined by the sensor resolution. The goal is to find the optimal number of planes $N^\star$ and assignment mask $M^\star$ that minimize the total model information $\Phi_{N,M}$. The information for each model is computed by considering the likelihood of points being assigned to planes or treated as outliers, with penalties for model complexity and sensor noise.

The information for a model with $N$ planes is given by:

$$\Phi_N = k\ln(N+1) + k_0 n \ln(R/\epsilon) + \sum_{i=1}^N \left[ n\ln(R/\epsilon) + k_i(n-1)\ln(R/\epsilon) + \sum_{j=1}^{k_i} \left( \frac{1}{2} \frac{(\bm{n}_i \cdot \bm{x}_j + d_i)^2}{\sigma^2} + \frac{1}{2} \ln \left( \frac{2\pi\sigma^2}{\epsilon^2} \right) \right) \right]$$

where $k_0$ is the number of outliers, $k_i$ is the number of inliers for plane $i$, $\bm{n}_i$ and $d_i$ are the plane parameters, and $\sigma$ is the sensor noise.

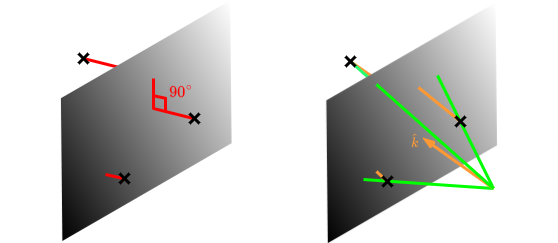
Figure 2: In the generalised plane detection problem, $\delta(\bm{x_i})$ is the normal distance between $\bm{x_i}$ and the plane, but for depth images, it is the parallel distance along the z-axis.

The assignment mask penalizes models with excessive planes, and the sensor noise model can be depth-dependent, further refining the information calculation.

Algorithmic Implementation

The algorithm proceeds by:

1. Generating candidate planes via repeated random sub-sampling.
2. Assigning points to planes or outlier status based on their contribution to information reduction.
3. Selecting the model with the minimum total information as the ground truth.
4. Ranking detected planes by their total information reduction.

To accelerate computation, semantic segmentation (e.g., using SAM) is used to partition the depth map, increasing the inlier ratio within each partition and reducing the search space.

Experimental Results

Synthetic Data

Experiments on synthetic depth images (staircase and tetrahedron scenes) with added Gaussian noise demonstrate that the proposed method accurately detects the true planes and rejects spurious planes generated from noise, unlike Open3D's RANSAC-based segmentation.

Figure 3: Depth image of a synthetic scene used for plane detection.

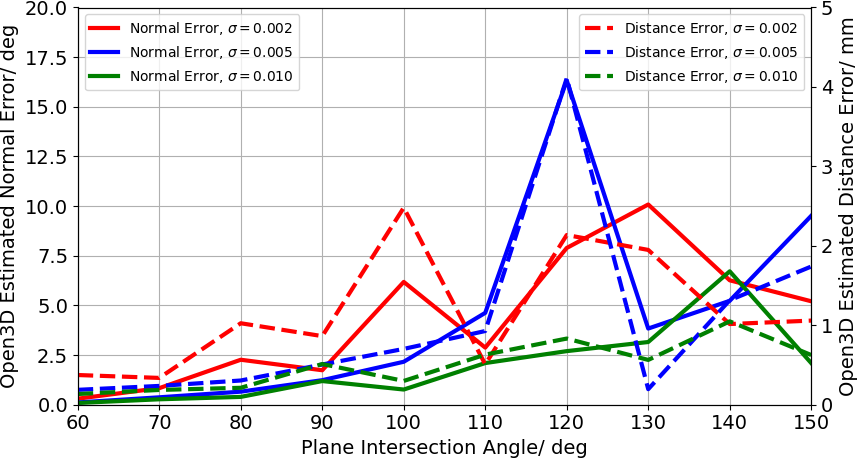
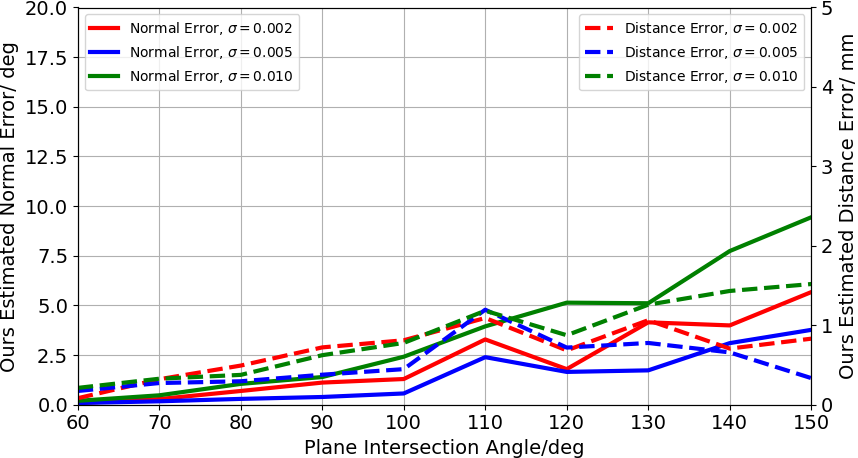
Figure 4: Graph of estimated normal and distance errors against plane intersection for both the Open3D and our approach. The scale of the x and y-axis are kept consistent between graphs.

The method also provides a ranking of plane quality, correctly ordering planes corrupted by sinusoidal noise according to their degradation.

Real-World Data (NYU-v2)

On the NYU-v2 dataset, the method outperforms neural network-based plane segmentation approaches in VOI, RI, and SC metrics, especially when using a proportional noise model. Qualitative results show improved segmentation of dominant planes and reduced fragmentation compared to ground truth masks.

Figure 5: RGB image from NYU-v2 dataset used for real-world plane detection.

Runtime and Limitations

The Python implementation averages 308 seconds per frame (including segmentation), while a C++ version reduces this to 21 seconds (without segmentation). The main limitation is ambiguity in mask assignment near plane intersections, which can be partially mitigated by post-processing based on surface normals, though this is sensitive to sensor noise.

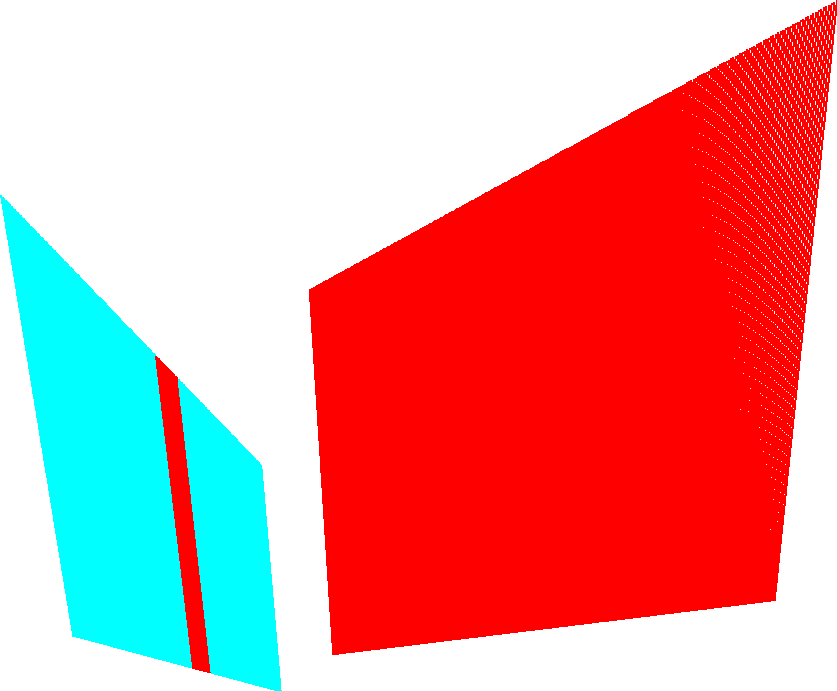
Figure 6: No post-processing: points along plane intersections may be misassigned due to ambiguity.

Practical and Theoretical Implications

The information-theoretic framework provides a rigorous, objective criterion for plane detection, eliminating the need for manual threshold tuning and reducing false positives. The approach is robust to sensor noise and adaptable to different sensor models. The ranking metric enables downstream applications to select high-quality planes for tasks such as navigation, mapping, and CAD model generation.

Theoretically, the method advances model selection in geometric computer vision by integrating discrete data constraints, sensor physics, and complexity penalties. It also highlights the limitations of current ground truth datasets and neural network training paradigms, suggesting that improved plane masks can enhance learning-based methods.

Future Directions

Future work may focus on concurrent estimation of all plane parameters (e.g., MultiRANSAC), integration of localised plane estimation methods, and further acceleration via parallelization or GPU implementation. Addressing intersection ambiguity and improving robustness to noise remain open challenges.

Conclusion

The proposed model information optimization framework for plane detection offers significant improvements over conventional RANSAC and neural network-based methods, both in accuracy and reliability. By leveraging information-theoretic principles and sensor models, the approach provides objective plane detection and ranking, with practical utility in robotics and computer vision. Further research may extend the framework to more complex scenes and enhance computational efficiency.