Towards Scalable Lottery Ticket Networks using Genetic Algorithms (2508.08877v1)

Abstract: Building modern deep learning systems that are not just effective but also efficient requires rethinking established paradigms for model training and neural architecture design. Instead of adapting highly overparameterized networks and subsequently applying model compression techniques to reduce resource consumption, a new class of high-performing networks skips the need for expensive parameter updates, while requiring only a fraction of parameters, making them highly scalable. The Strong Lottery Ticket Hypothesis posits that within randomly initialized, sufficiently overparameterized neural networks, there exist subnetworks that can match the accuracy of the trained original model-without any training. This work explores the usage of genetic algorithms for identifying these strong lottery ticket subnetworks. We find that for instances of binary and multi-class classification tasks, our approach achieves better accuracies and sparsity levels than the current state-of-the-art without requiring any gradient information. In addition, we provide justification for the need for appropriate evaluation metrics when scaling to more complex network architectures and learning tasks.

• The paper presents a genetic algorithm-based method to discover lottery ticket subnetworks that match the performance of full networks.
• It employs binary masks with evolutionary strategies like mutation and crossover to optimize for both accuracy and sparsity.
• Experimental results show GA outperforms edge-popup methods in binary classification while highlighting challenges for multi-class tasks.

Towards Scalable Lottery Ticket Networks using Genetic Algorithms

Introduction

The paper "Towards Scalable Lottery Ticket Networks using Genetic Algorithms" presents an innovative approach to identifying and leveraging strong lottery ticket networks, which are subnetworks capable of performing as well as their overparameterized counterparts without any training. The focus is on utilizing genetic algorithms (GA) for uncovering these subnetworks, thus improving the scalability and computational efficiency of deep learning models.

The research extends current understanding of the Strong Lottery Ticket Hypothesis (SLTH), proposing that complexity in neural networks can be drastically reduced without sacrificing performance. By employing GAs, the paper capitalizes on architecture-agnostic search methods that do not rely on gradients, therefore being applicable to non-differentiable models as well.

Methodology

Genetic Algorithms for Network Pruning

The genetic algorithm design involves several key components. Candidate subnetworks are represented using binary masks that dictate which parameters of an original overparameterized network should be retained. The evolution of these subnetworks focuses on optimizing two criteria: accuracy on validation datasets and sparsity of the network to ensure efficiency.

The primary sequence involves initializing a population of random binary masks and evolving these through iterations using genetic operators:

• Selection: Lexical selection prioritizes accuracy first, ensuring minimal performance degradation.
• Mutation and Recombination: Random bit flips in masks (mutation) and crossover operations between highly performing masks help explore larger solution spaces.
• Fitness Evaluation: Measured primarily by accuracy, with a secondary objective of sparsity, using a population of binary masks applied to the networks.

Optimization Strategy

The approach allows direct optimization without needing the intermediary loss landscape that gradient descent typically navigates. Important steps include an adaptive accuracy boundary during initial population generation to enhance starting performance levels of candidate solutions.

Experimental Setup

The experiments investigate several datasets and neural architectures of varying complexities. These include simple binary classification problems like the Moons and Circles datasets, and more complex multi-class tasks using synthetic Blobs and the Digits dataset.

• Architectures Utilized: Four feedforward networks varying from small to large parameter counts.
• Comparative Baselines: Traditional backpropagation and edge-popup algorithm serve as the comparative benchmarks.
• Hyperparameters: Detailed exploration of parameters like population size and mutation/recombination rates ensures effective search by the GAs.

Results

Binary Classification

For binary classification tasks (Moons and Circles), the GA consistently identified subnetworks with competitive accuracy to traditionally trained networks. Larger architectures benefited more from the evolutionary search, showcasing the ability of GAs to find performant subnetworks even in highly parameterized spaces.

Figure 1: Visualization of a lottery ticket network demonstrating how subnetworks perform comparably to full networks but are highly sparse.

Comparison with Edge-Popup

Edge-popup, which trains masks through gradient estimates, was less effective in these tasks when compared to GA discoveries, especially given its reliance on specific initialization schemes. GA's initialization with uniform distributions performed favorably, suggesting robustness across initial conditions.

Multi-Class Classification

In more complex scenarios, such as the Digits dataset, the GA demonstrated limitations, particularly in handling increased class numbers. Transitioning from accuracy to cross-entropy loss as the objective function improved outcomes, as it guided the GA away from suboptimal local minima characterized by uncertain class predictions.

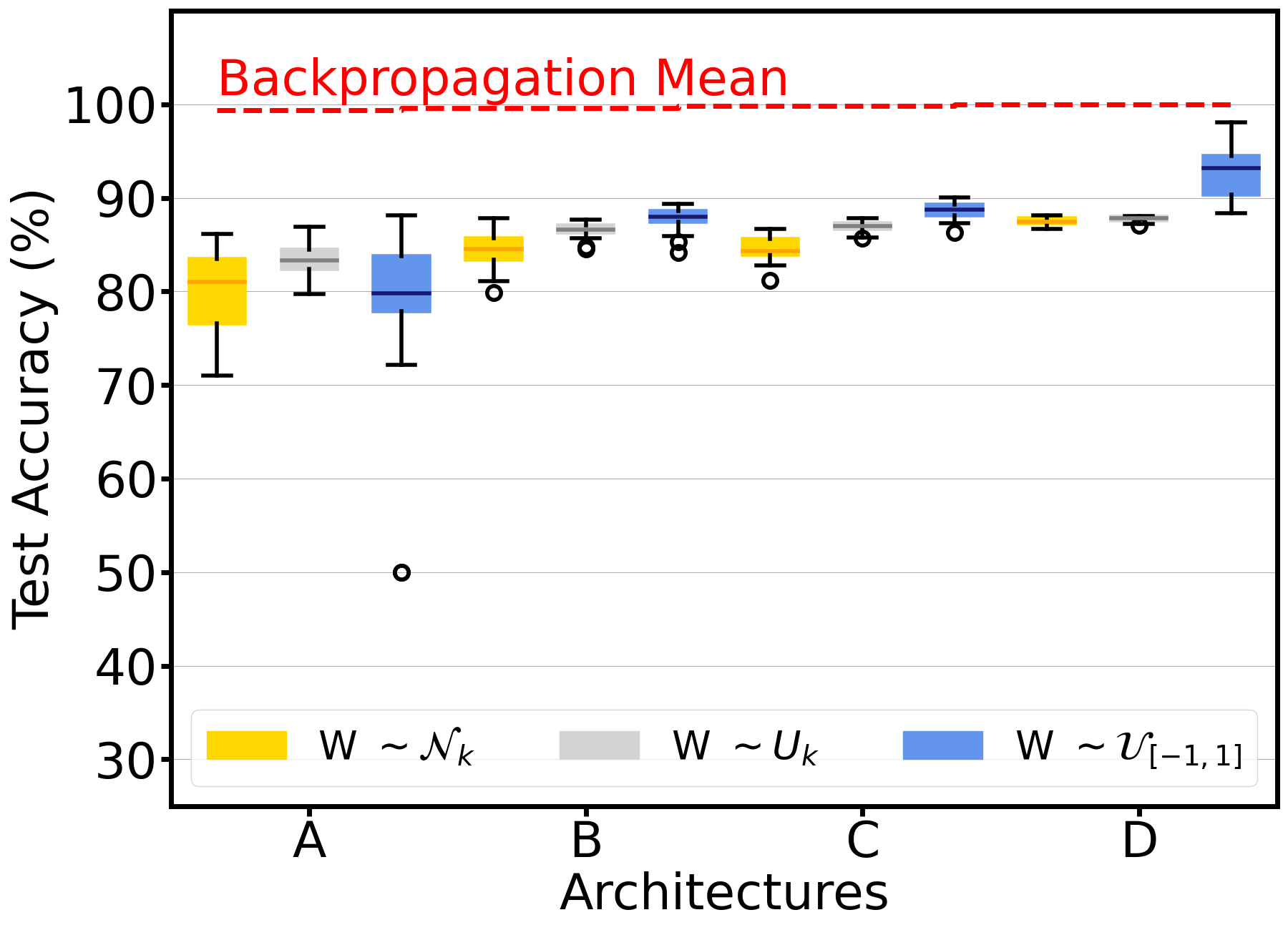
Figure 2: Edge-popup's performance visualization indicating variability across initialization conditions.

Scalability

The scalability of the GA approach is highlighted by its performance across different architectures and tasks. While initialization and mask adaptation strategies offer substantial benefits, further enhancements are possible, particularly by integrating more domain-specific insights into parameter choices and evolutionary strategies.

Conclusion

This work illuminates the possibility of exploiting inherent redundancies in neural networks through genetic algorithms, providing substantial reductions in size and training complexity via the SLTH framework. Future directions include exploring further algorithmic refinements, broader applications across architectures, and optimizing initialization strategies to capitalize on randomly endowed strong subnetworks. The method sets a precedent for sustainable and scalable AI, offering significant energy efficiency and reduced training times for complex models. The post-processing pruning strategy also suggests further potential for model optimization and deployment.