Inference-Time Scaling of Diffusion Language Models with Particle Gibbs Sampling (2507.08390v1)

Abstract: Discrete diffusion models have emerged as a powerful paradigm for language modeling, rivaling auto-regressive models by training-time scaling. However, inference-time scaling in discrete diffusion models remains relatively under-explored. In this work, we study sampling-based approaches for achieving high-quality text generation from discrete diffusion models in reward-guided settings. We introduce a novel inference-time scaling approach based on particle Gibbs sampling for discrete diffusion models. The particle Gibbs sampling algorithm iteratively refines full diffusion trajectories using conditional Sequential Monte Carlo as its transition mechanism. This process ensures that the updated samples progressively improve and move closer to the reward-weighted target distribution. Unlike existing inference-time scaling methods, which are often limited to single diffusion trajectories, our approach leverages iterative refinement across multiple trajectories. Within this framework, we further analyze the trade-offs between four key axes for inference-time scaling under fixed compute budgets: particle Gibbs iterations, particle count, denoising steps, and reward estimation cost. Empirically, our method consistently outperforms prior inference-time strategies on reward-guided text generation tasks, achieving significant improvement in accuracy under varying compute budgets.

• The paper introduces PG-DDM, a novel Particle Gibbs sampling method that iteratively refines diffusion trajectories for reward-guided text generation.
• It employs conditional Sequential Monte Carlo as a transition kernel, achieving state-of-the-art results in tasks like toxicity control and sentiment generation.
• The method strategically balances particle count and iterations to optimize computational budgets while maintaining high generation quality.

Inference-Time Scaling of Diffusion LLMs with Particle Gibbs Sampling

Introduction

This paper introduces a novel approach to inference-time scaling in discrete diffusion models using Particle Gibbs sampling, a strategy designed to enhance reward-guided text generation. The method iteratively refines trajectories to better approximate a reward-weighted target distribution, offering significant improvements over traditional single-trajectory scaling techniques in practical applications such as controlled text generation.

Methodology

The core contribution is the Particle Gibbs for Discrete Diffusion Models (PG-DDM), which iteratively refines diffusion trajectories. The algorithm leverages conditional Sequential Monte Carlo (SMC) as a transition kernel, ensuring that updated samples progressively move closer to the desired distribution. This process allows for simultaneous consideration of multiple trajectories, in contrast to existing methods constrained to single trajectory refinement.

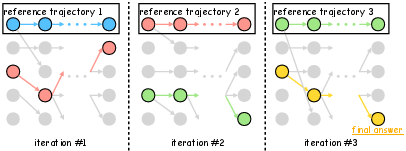
Figure 1: Illustration of the PG-DDM algorithm. At each iteration, a reference trajectory is fixed (top row), and new particles are generated and resampled (gray). One trajectory becomes the next reference (colored), enabling iterative refinement. The final output is selected after multiple iterations.

The approach is analyzed across four axes: particle Gibbs iterations, particle count, denoising steps, and reward estimation cost. The results show that PG-DDM consistently outperforms prior strategies on reward-guided generation tasks, demonstrating substantial improvements in accuracy under fixed computational budgets.

Experimental Results

Empirical evaluations were conducted on tasks such as toxicity control and sentiment generation. PG-DDM achieved state-of-the-art performance, particularly in maintaining the balance between reward maximization and generation quality. The tests demonstrate the utility of PG-DDM under varying scales of compute allocation, supporting the theoretical convergence claims.

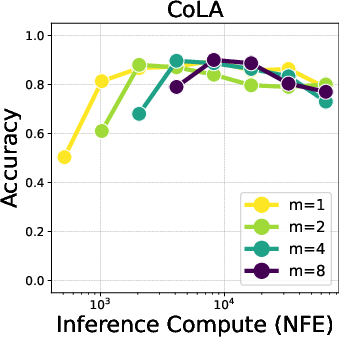
Figure 2: Trade-off between particle Gibbs iterations ($m$) and particle counts (x-axis) across varying compute budgets. Increasing particles (with $m = 1$) performs best in low-NFE regimes. However, as particle count saturates, additional PG iterations ($m = 2, 4$) become more effective.

Implementation Considerations

This approach involves significant computational consideration, particularly in the optimal allocation of compute budgets across identified scaling axes. The method requires careful tuning of the number of iterations, particle counts, and other parameters to balance reward optimization with computational overhead effectively.

A critical aspect is the strategic allocation of computational resources to various axes. As particle count scaling saturates, emphasis should shift toward increasing iterations to maintain efficiency. The inclusion of advanced transition kernels and evaluation functions further enhances performance but requires additional resource planning.

Conclusion

The introduction of PG-DDM offers a sophisticated framework for inference-time scaling in diffusion LLMs, providing both theoretical robustness and empirical efficacy. Future research could explore further extensions involving adaptive mechanisms for dynamically allocating computational resources based on real-time performance feedback, thereby enhancing the practical utility of the algorithm in more complex scenarios.