LeanConjecturer: Automatic Generation of Mathematical Conjectures for Theorem Proving (2506.22005v1)

Abstract: We introduce LeanConjecturer, a pipeline for automatically generating university-level mathematical conjectures in Lean 4 using LLMs. Our hybrid approach combines rule-based context extraction with LLM-based theorem statement generation, addressing the data scarcity challenge in formal theorem proving. Through iterative generation and evaluation, LeanConjecturer produced 12,289 conjectures from 40 Mathlib seed files, with 3,776 identified as syntactically valid and non-trivial, that is, cannot be proven by \texttt{aesop} tactic. We demonstrate the utility of these generated conjectures for reinforcement learning through Group Relative Policy Optimization (GRPO), showing that targeted training on domain-specific conjectures can enhance theorem proving capabilities. Our approach generates 103.25 novel conjectures per seed file on average, providing a scalable solution for creating training data for theorem proving systems. Our system successfully verified several non-trivial theorems in topology, including properties of semi-open, alpha-open, and pre-open sets, demonstrating its potential for mathematical discovery beyond simple variations of existing results.

• The paper presents a novel pipeline that combines rule-based context extraction with LLM-based generation to produce thousands of valid, nontrivial mathematical conjectures.
• It addresses data scarcity in theorem proving by leveraging Mathlib seed files and ensuring syntactic validity, novelty, and non-triviality through automated post-processing.
• The iterative process and GRPO learning experiments demonstrate scalable improvements in proof success rates, paving the way for enhanced formal verification.

LeanConjecturer: Automatic Generation of Mathematical Conjectures for Theorem Proving

The paper "LeanConjecturer: Automatic Generation of Mathematical Conjectures for Theorem Proving" (2506.22005) presents an innovative pipeline leveraging LLMs for the automatic generation of formal mathematical conjectures. By addressing the data scarcity issue, this novel approach provides a scalable method to enhance the performance of theorem proving systems using Lean 4. The following sections detail the methods, results, and implications of this research.

Introduction

In recent years, the application of LLMs in formal theorem proving has gained substantial traction, targeting improvements in automated mathematical reasoning capabilities. Despite significant advancements such as DeepSeek-Prover-V2 achieving remarkable accuracy on benchmarks like MiniF2F, a major limitation persists: the scarcity of high-quality, formal training data. This challenge is compounded by the vast availability of informal mathematical data, in stark contrast to the limited scope of Clean's Mathlib.

In response to the "triviality trap," LeanConjecturer proposes a hybrid pipeline combining rule-based context extraction with LLM-based theorem generation. By generating novel mathematical conjectures without requiring machine-verifiable proofs, LeanConjecturer provides a promising mechanism to create training data necessary for advancing theorem proving systems.

Methodology

Generation

LeanConjecturer employs Mathlib seed files to drive the generation of new mathematical conjectures. A systematic hybrid approach is adopted, utilizing rule-based context extraction while leveraging LLMs for generating theorem statements. The LLM is tasked to produce theorems with specified instructions, such as the emphasis on generating as many conjectures as possible, regardless of input size.

To prevent output errors, generated theorems are post-processed by removing prefixes and unnecessary parts, and they are automatically augmented with necessary Lean imports and contexts. This structured methodology enhances compatibility with the Lean 4 proof assistant.

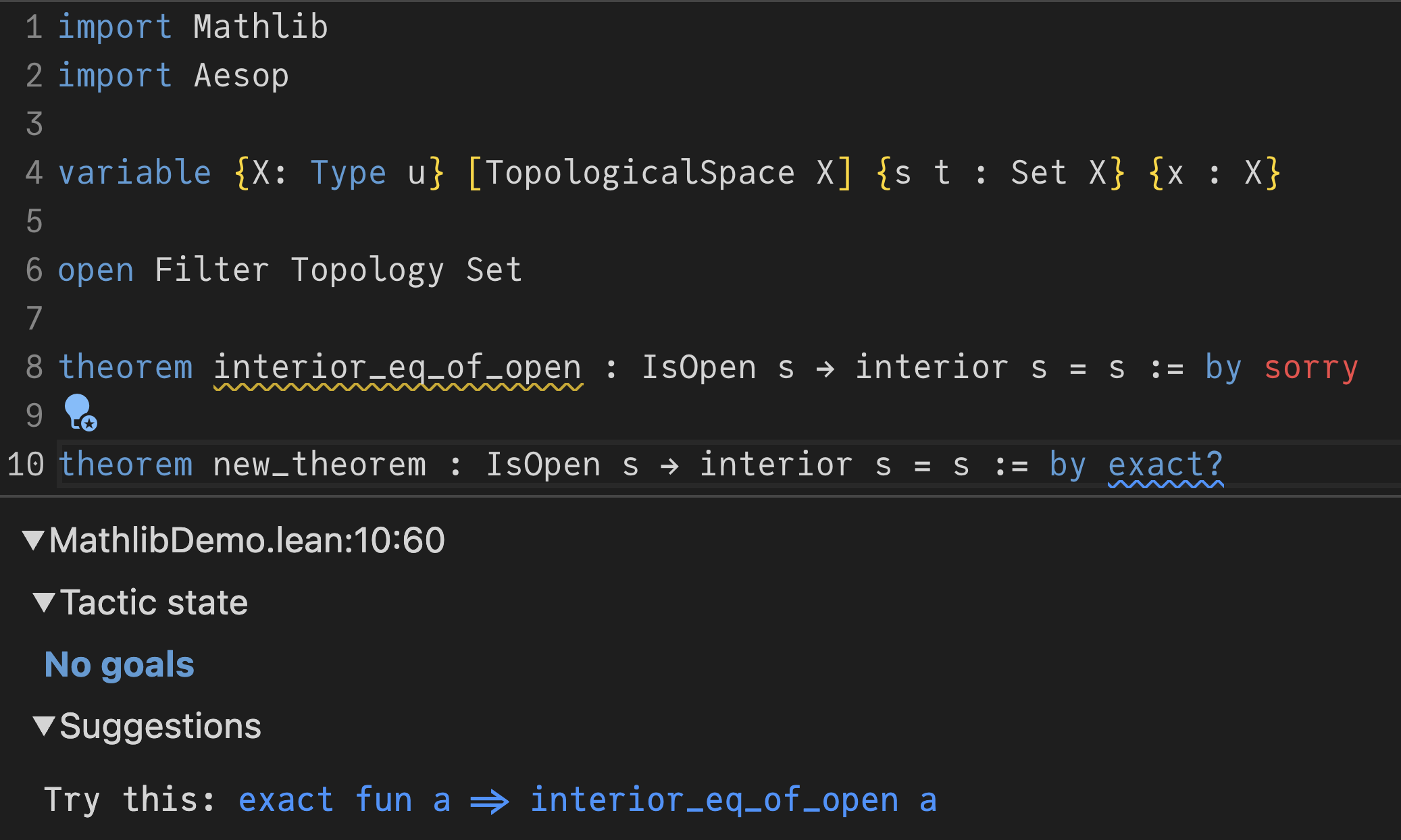
Figure 1: Illustration of novelty assessment using exact? command with context. By including previously generated conjectures in the context, we can effectively detect and filter out duplicate or similar conjectures, ensuring the generation of truly novel mathematical statements.

Evaluation

The evaluation phase of LeanConjecturer is essential for identifying conjectures suitable for theorem provers and refining subsequent iterations. It involves checking:

• Syntactic Validity: Conjectures need to be parseable in Lean 4.
• Novelty: Direct verification is conducted through Lean's exact? command to ensure conjectures are novel compared to Mathlib and previous iterations.
• Non-Triviality: The aesop tactic checks for automatic provability; conjectures need to be unprovable by aesop to be deemed non-trivial.

This evaluation ensures the generation of high-quality and novel mathematical conjectures while excluding duplicates.

Iteration

LeanConjecturer adopts an iterative process to enhance conjecture novelty and diversity. The selected conjectures are aggregated into new files, forming the base for further generation rounds until minimal novel conjectures are produced. This iterative process prevents repetition and fosters mathematical exploration.

Results and Experiments

Conjecture Generation

The LeanConjecturer pipeline was tested on 40 Mathlib files, producing 12,289 conjectures, with 3,776 classified as novel and non-trivial. The average generation rate per file was 103.25. The specific role of the "as many as possible" prompt was highlighted as crucial in optimizing the generation volume.

GRPO Learning

Experiments expanded to include targeted GRPO (Group Relative Policy Optimization) learning, focusing on topology-related conjectures and numerical results demonstrated performance scalability. The per-proof success improved to 5307/24576 attempts, with a modest problem success rate increase to 50/192 over 34 GRPO epochs. The transfer of enhanced skills to new concept categories like alpha-open sets suggested the potential for cross-domain application.

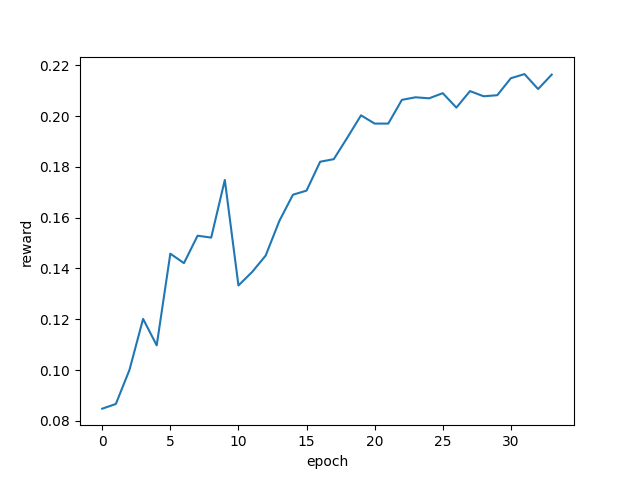
Figure 2: Learning curve of GRPO training over 34 epochs. The graph shows the improvement in proof success rates and problem success rates as training progresses.

Conclusion

LeanConjecturer offers a robust pipeline for addressing the persistent data scarcity issues in formal theorem proving by automating conjecture generation with LLMs. Its hybrid rule-based and LLM approach generates a substantial volume of valid, novel, and non-trivial conjectures. The integration of GRPO learning further advances theorem provers' capabilities. Despite challenges such as syntactic errors and computational demands, LeanConjecturer marks a significant advancement in scalable synthetic data generation for formal mathematical proofs and points toward future developments in open-ended learning systems. The availability of the associated implementation and its results provides a firm foundation for future research and applications in the domain.