Learning Equivariant Models by Discovering Symmetries with Learnable Augmentations (2506.03914v2)

Abstract: Recently, a trend has emerged that favors shifting away from designing constrained equivariant architectures for data in geometric domains and instead (1) modifying the training protocol, e.g., with a specific loss and data augmentations (soft equivariance), or (2) ignoring equivariance and inferring it only implicitly. However, both options have limitations, e.g., soft equivariance still requires a priori knowledge about the underlying symmetries, while implicitly learning equivariance from data lacks interpretability. To address these limitations, we propose SEMoLA, an end-to-end approach that jointly (1) discovers a priori unknown symmetries in the data via learnable data augmentations, and uses them to (2) encode the respective approximate equivariance into arbitrary unconstrained models. Hence, it enables learning equivariant models that do not need prior knowledge about symmetries, offer interpretability, and maintain robustness to distribution shifts. Empirically, we demonstrate the ability of SEMoLA to robustly discover relevant symmetries while achieving high prediction performance across various datasets, encompassing multiple data modalities and underlying symmetry groups.

• The paper introduces SEMoLA, which discovers unknown dataset symmetries using learnable augmentations to encode approximate equivariance.
• The methodology applies Lie theory and a weighted multi-task loss to balance empirical performance and symmetry learning across diverse domains.
• Experimental results on RotatedMNIST, N-body dynamics, and QM9 demonstrate superior prediction accuracy and adaptability under distribution shifts.

Learning Equivariant Models by Discovering Symmetries with Learnable Augmentations

Introduction

The paper "Learning Equivariant Models by Discovering Symmetries with Learnable Augmentations" introduces SEMoLA, an innovative approach aimed at learning equivariant models without prior knowledge about symmetries in datasets. SEMoLA leverages learnable data augmentations to discover a priori unknown symmetries, which are then used to encode approximate equivariance into arbitrary unconstrained models. This proposal offers a balance between robustness, interpretability, and flexibility in model design, presenting advantages over both hard and soft equivariant models by focusing on datasets within geometric domains with assumed unknown symmetries.

Methodology

LieAugmenter:

Central to SEMoLA is the LieAugmenter module, which employs Lie theory to model continuous symmetries. By parameterizing the elements of a matrix Lie group $G$ through its generators (a Lie algebra basis), SEMoLA reparameterizes the group elements using learnable basis parameters optimized during training. Each basis element is initialized to ensure stability with a consistent norm, and augmentations are applied by sampling Lie group elements and transforming the input data appropriately.

Training:

The model training uses a weighted multi-task loss function, combining empirical loss, equivariance loss, and regularization terms that emphasize augmentations' properties and basis orthogonality and sparsity. The distinct weights in the multi-task objective enable balancing between prediction accuracy and symmetry learning.

Inference:

For inference, two main strategies are proposed: processing augmentations to average their predicted outputs or evaluating unaugmented inputs for enhanced inference speed. This flexibility addresses different application needs regarding speed and accuracy.

Experimental Analysis

SEMoLA was evaluated across multiple datasets, showcasing its ability to discover symmetries robustly, achieve high prediction performance, and maintain low equivariance errors.

RotatedMNIST Dataset:

SEMoLA achieved accuracies close to the optimal performance of CNNs using ground-truth augmentations, demonstrating robustness even when data distributions shifted. Notably, SEMoLA outperformed LieGAN and Augerino+, especially in out-of-distribution scenarios.

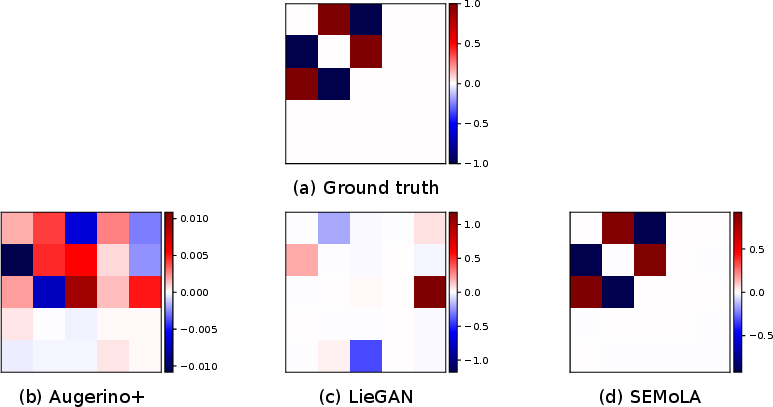
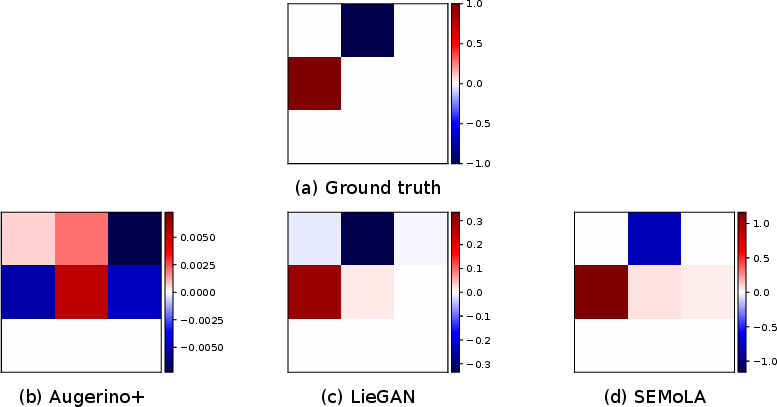
Figure 1: Comparison of the ground truth Lie algebra basis with those learned by LieGAN, Augerino+, and our proposed SEMoLA approach for the in-distribution version of the RotatedMNIST dataset (left) and the restricted out-of-distribution version (right).

N-Body Dynamics:

The model accurately learned rotational symmetries in a simulated two-body problem, even under distributional constraints. SEMoLA showed competitive prediction accuracy close to hard-equivariant models like EMLP.

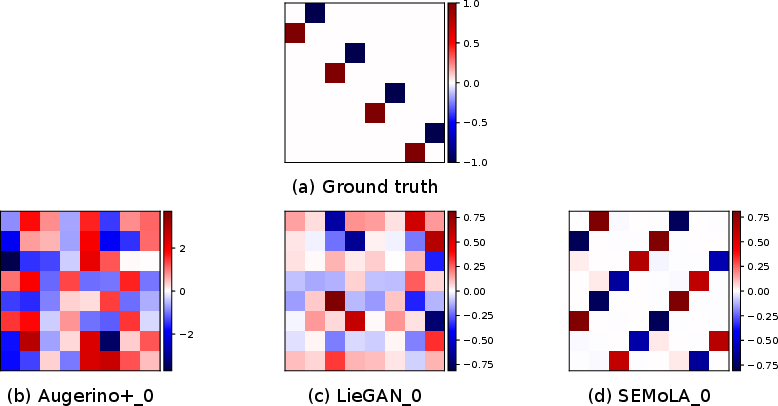
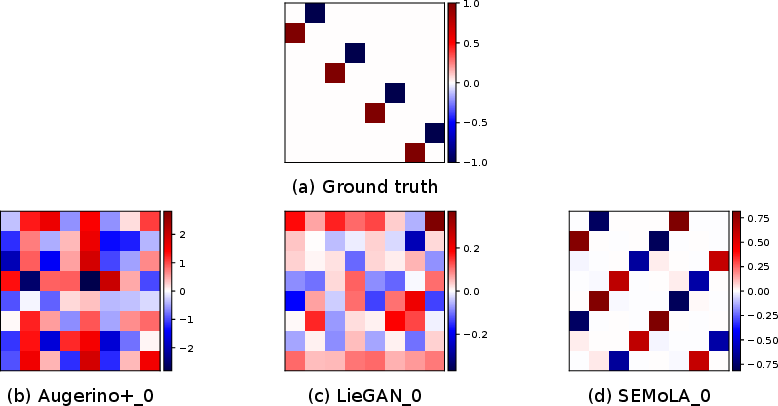
Figure 2: Comparison of the ground truth Lie algebra basis with those learned by LieGAN, Augerino+, and our proposed SEMoLA approach for the in-distribution version of the 2-body dataset (left) and the restricted out-of-distribution version (right) with one input and output timestep.

QM9 Dataset:

For complex molecular property prediction tasks, SEMoLA achieved substantial improvements in prediction accuracy compared to unconstrained and augmented models, achieving results comparable to full SE(3) equivariant models.

Figure 3: Comparison of the ground truth Lie algebra basis and those learned by SEMoLA for the HOMO and LUMO targets of the QM9 dataset.

Implications and Future Directions

SEMoLA addresses significant challenges in deploying equivariant models, particularly when dataset symmetries are unknown or hard-to-specify, being particularly applicable in scientific domains like chemistry and physics. The advancements in interpretability, flexibility, and suitability for various architectures (including CNNs, ViTs, and EfficientNets) suggest vast potential for SEMoLA across diverse machine learning applications.

Future directions for SEMoLA include exploring learnable augmentations for non-connected or nonlinear symmetries, extending its applicability to tasks without clearly defined symmetries, and optimizing its architecture to handle real-world scenarios with large-scale, high-dimensional data.

Conclusion

SEMoLA represents a significant step towards designing flexible, robust, and interpretable equivariant models in machine learning by effectively discovering and utilizing unknown data symmetries. Its generalizability to different data modalities and underlying symmetry groups, alongside competitive performance even under distribution shifts, positions it as a promising tool for augmenting unconstrained models with learned symmetry information.