Relaxed Equivariance via Multitask Learning (2410.17878v2)

Abstract: Incorporating equivariance as an inductive bias into deep learning architectures to take advantage of the data symmetry has been successful in multiple applications, such as chemistry and dynamical systems. In particular, roto-translations are crucial for effectively modeling geometric graphs and molecules, where understanding the 3D structures enhances generalization. However, equivariant models often pose challenges due to their high computational complexity. In this paper, we introduce REMUL, a training procedure for approximating equivariance with multitask learning. We show that unconstrained models (which do not build equivariance into the architecture) can learn approximate symmetries by minimizing an additional simple equivariance loss. By formulating equivariance as a new learning objective, we can control the level of approximate equivariance in the model. Our method achieves competitive performance compared to equivariant baselines while being $10 \times$ faster at inference and $2.5 \times$ at training.

• The paper introduces REMUL, a novel training procedure that approximates equivariance through multitask learning to reduce computational complexity while preserving performance.
• It presents specific metrics using group transformation evaluations to quantify how closely models approximate symmetry, bridging theoretical and practical aspects.
• Experiments in N-body dynamics, motion capture, and molecular dynamics demonstrate REMUL's superior efficiency and adaptability over traditional equivariant architectures.

Relaxed Equivariance via Multitask Learning

Abstract

This paper introduces REMUL, a training procedure that addresses the challenges posed by equivariant models in deep learning architectures, such as high computational complexity and scalability issues. By approximating equivariance using multitask learning, REMUL minimizes an additional equivariance loss, allowing unconstrained models to learn approximate symmetries. The REMUL procedure demonstrates competitive performance compared to equivariant baselines while significantly improving inference and training speeds.

Introduction

Equivariant machine learning models are pivotal in various domains, exploiting data symmetries like translations and rotations to handle complex structures effectively. However, these models often come with high computational costs and design constraints. REMUL presents a novel approach to achieving equivariance using a relaxed objective, enabling unconstrained models like Transformers and GNNs to approximate equivariance efficiently.

REMUL Training Procedure

REMUL redefines equivariance as a multitask learning objective, replacing constrained optimization with soft constraints through weighted loss functions. This approach provides flexibility in controlling the extent of equivariance based on task requirements, balancing generalization and symmetry. The penalty parameters, adjusted using constant or gradual methods like GradNorm, dynamically steer the learning process, enhancing the model's adaptability.

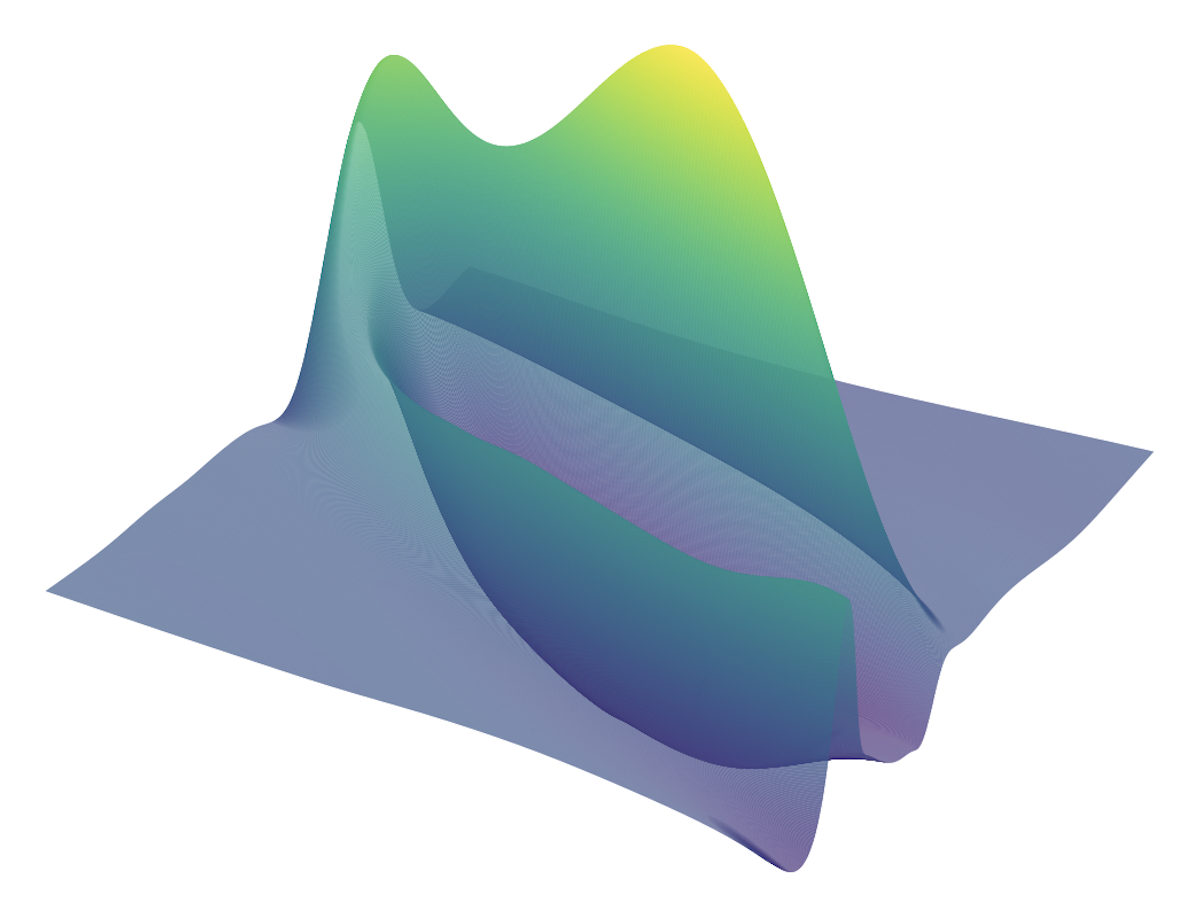
Figure 1: Geometric Algebra Transformer.

Quantifying Learned Equivariance

The paper introduces metrics to evaluate learned equivariance through group transformations, offering insights into how closely models approximate symmetry across data distributions. Two measures detail this approximation—one averaging discrepancies over group transformations and another assessing individual transformation differences. These tools bridge the gap between theoretical symmetries and practical model performance.

Experiments and Results

N-Body Dynamical System

In tasks like dynamical systems, REMUL significantly reduces equivariance error compared to traditional architectures like SE(3)-Transformers and Geometric Algebra Transformers. Despite having a near-zero equivariance error, equivariant models don't always guarantee superior prediction accuracy, highlighting the nuanced role of symmetry in learning dynamics.

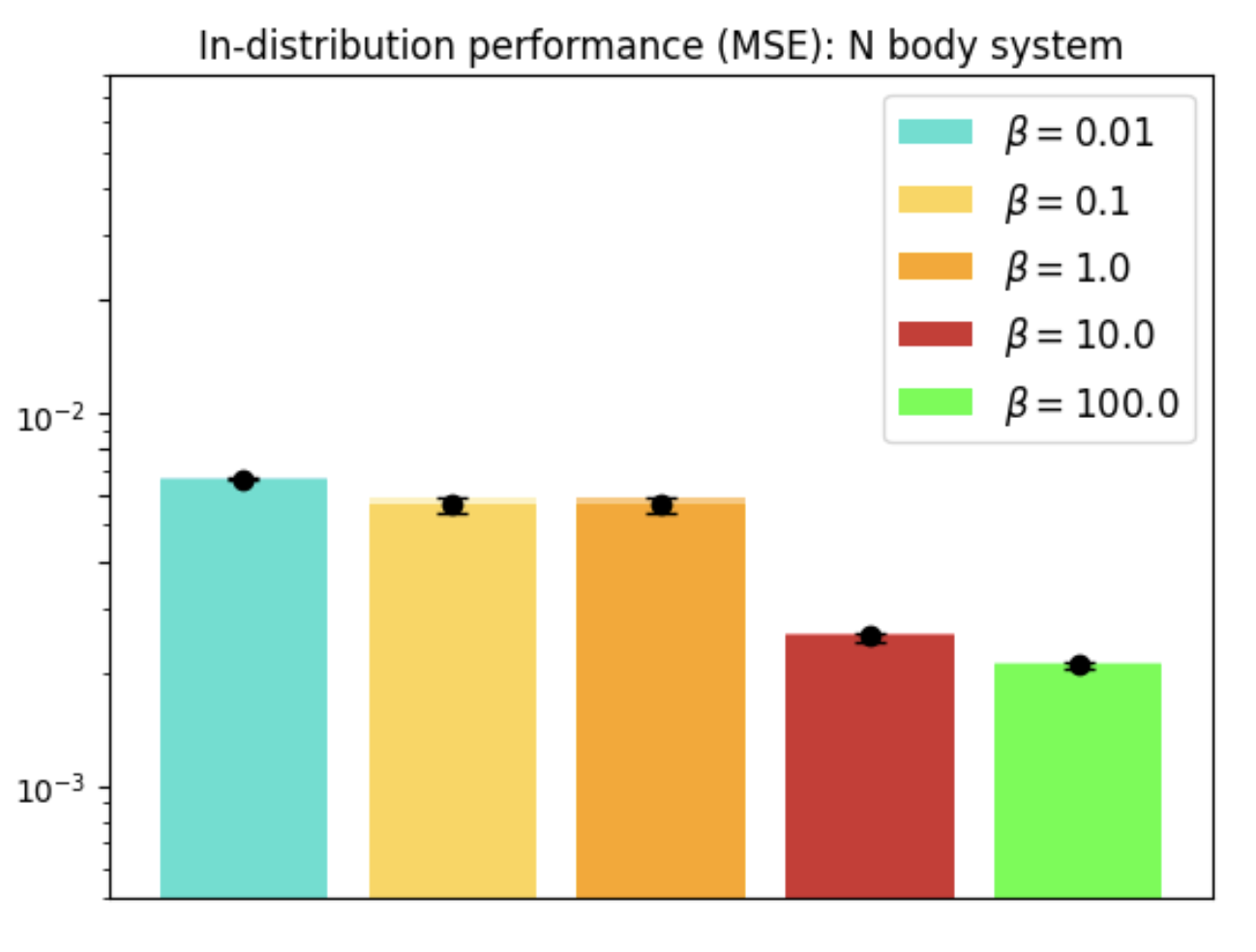
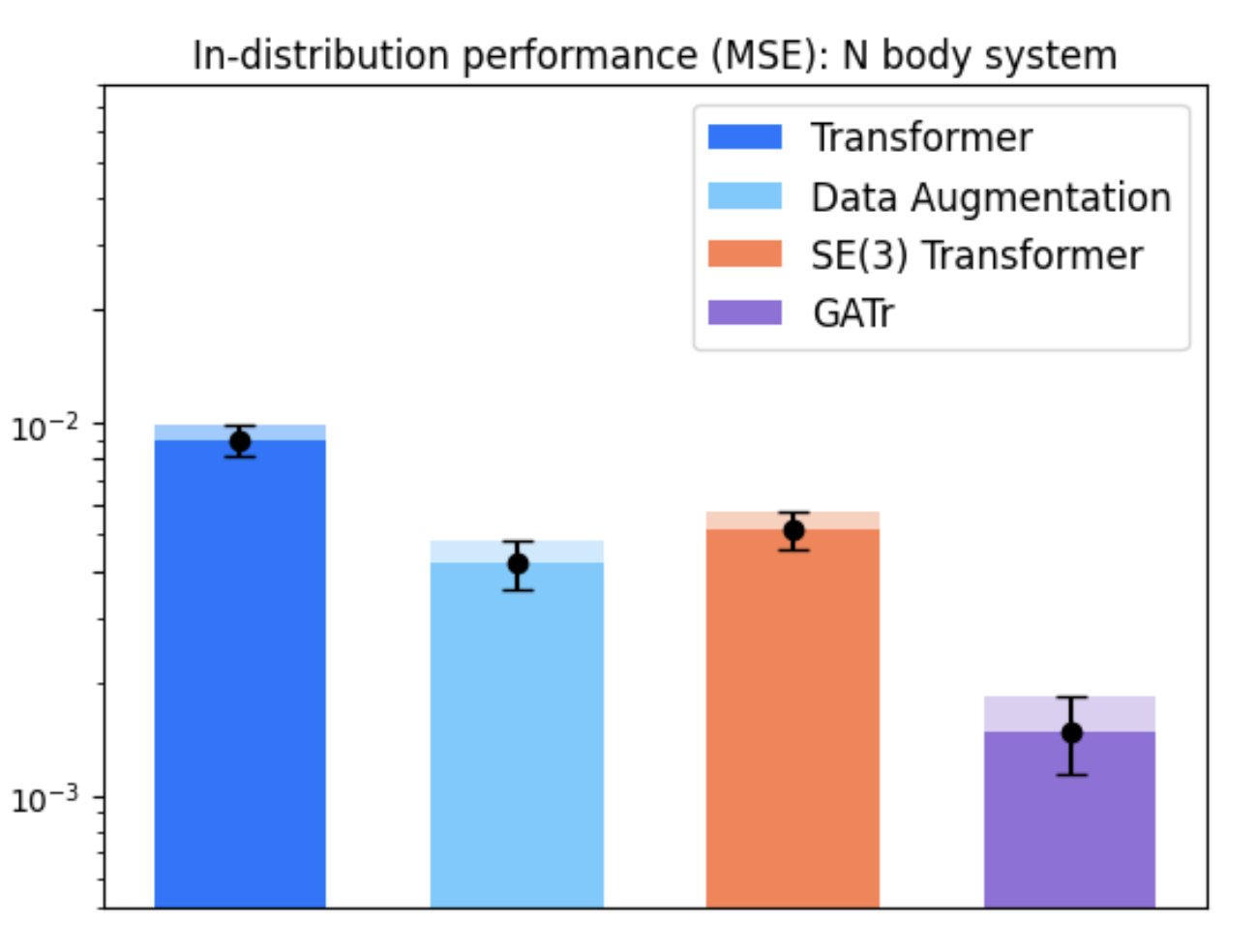
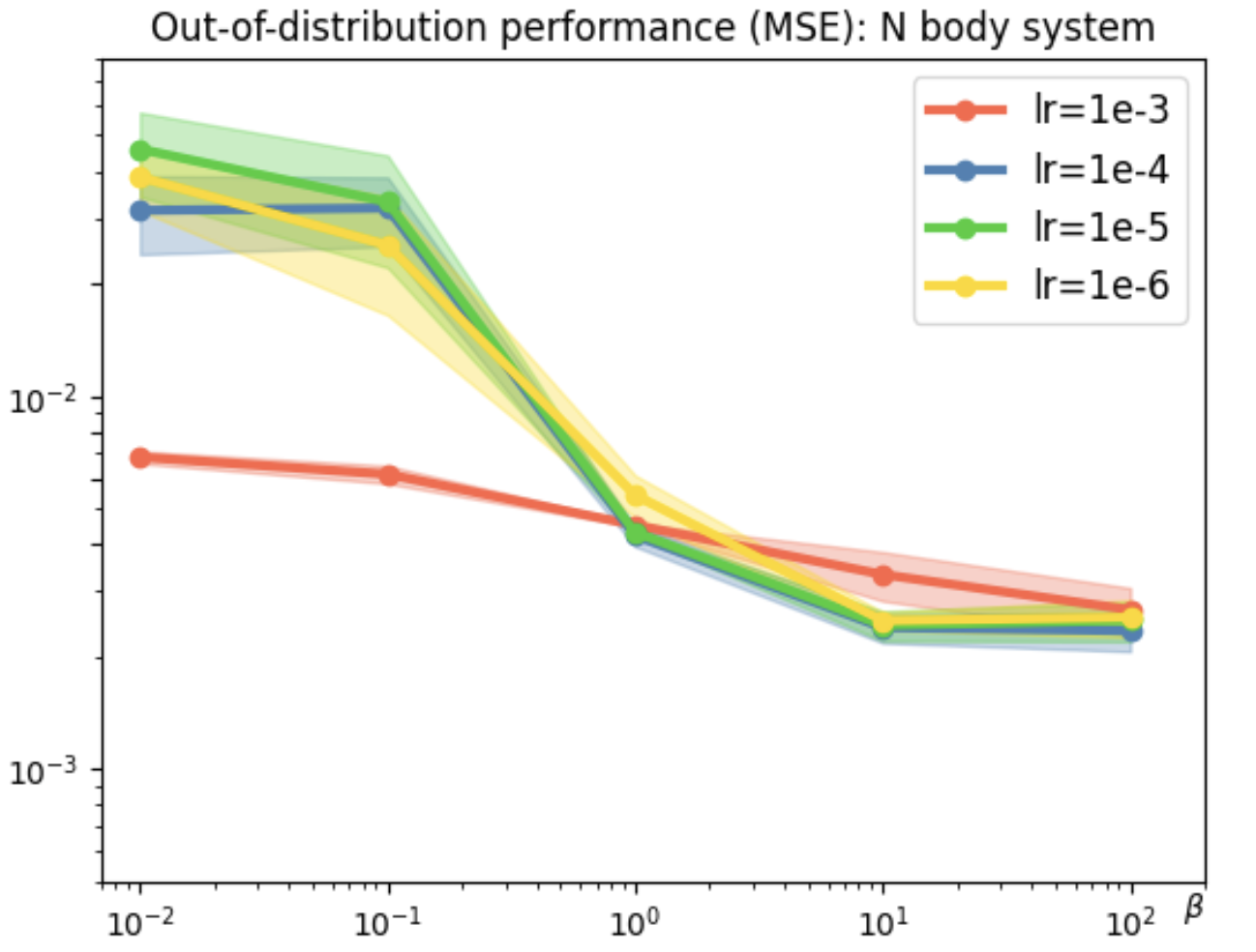
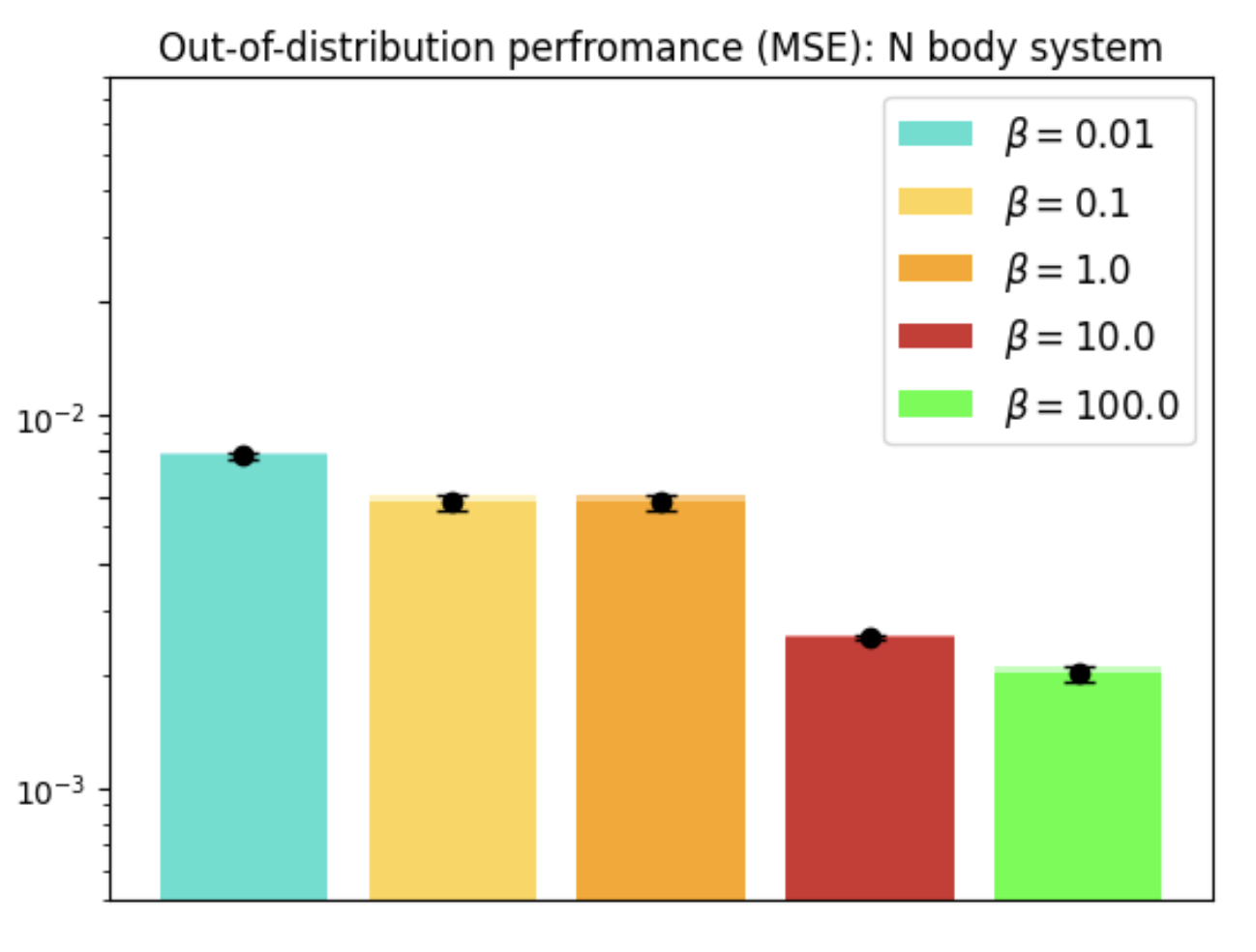
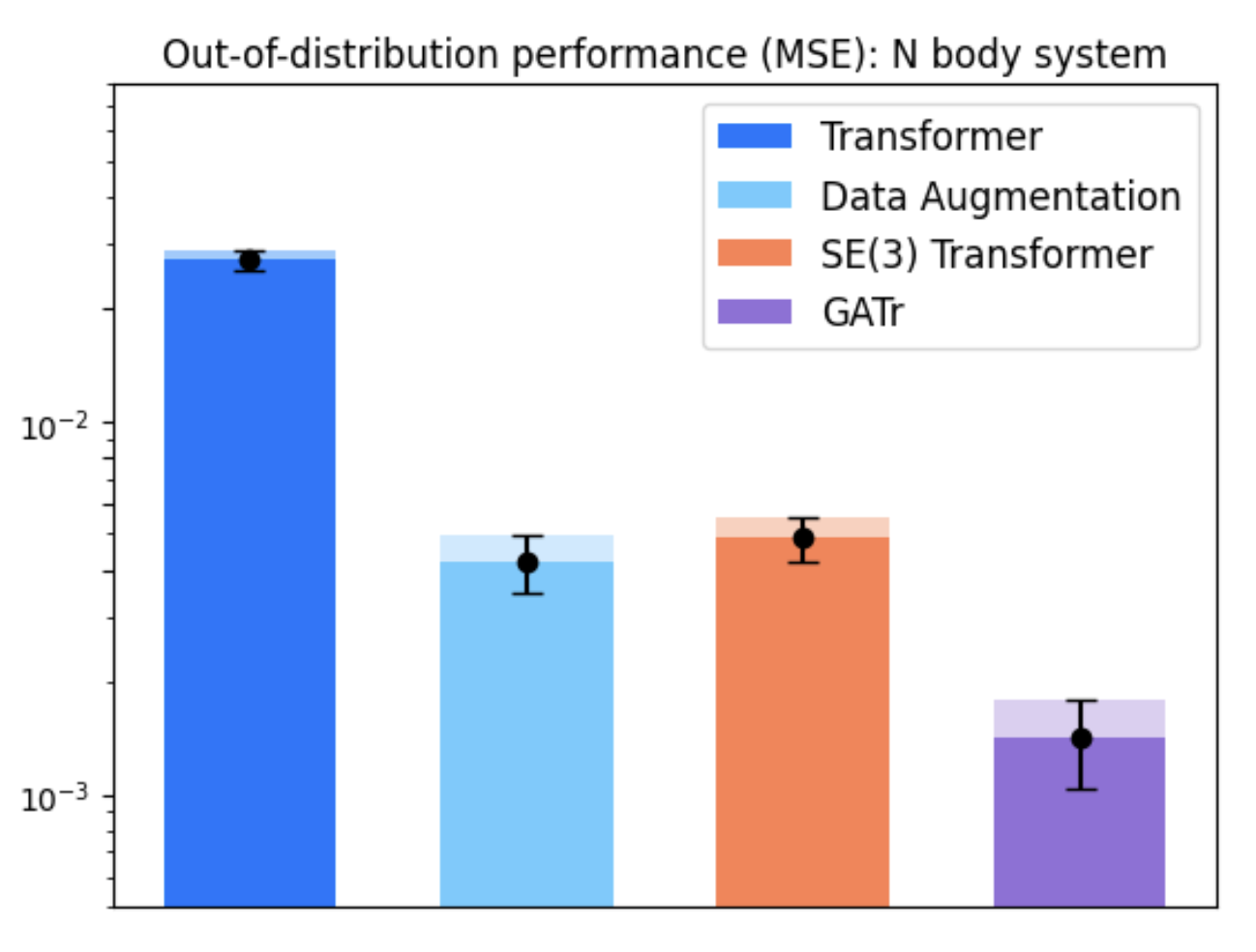
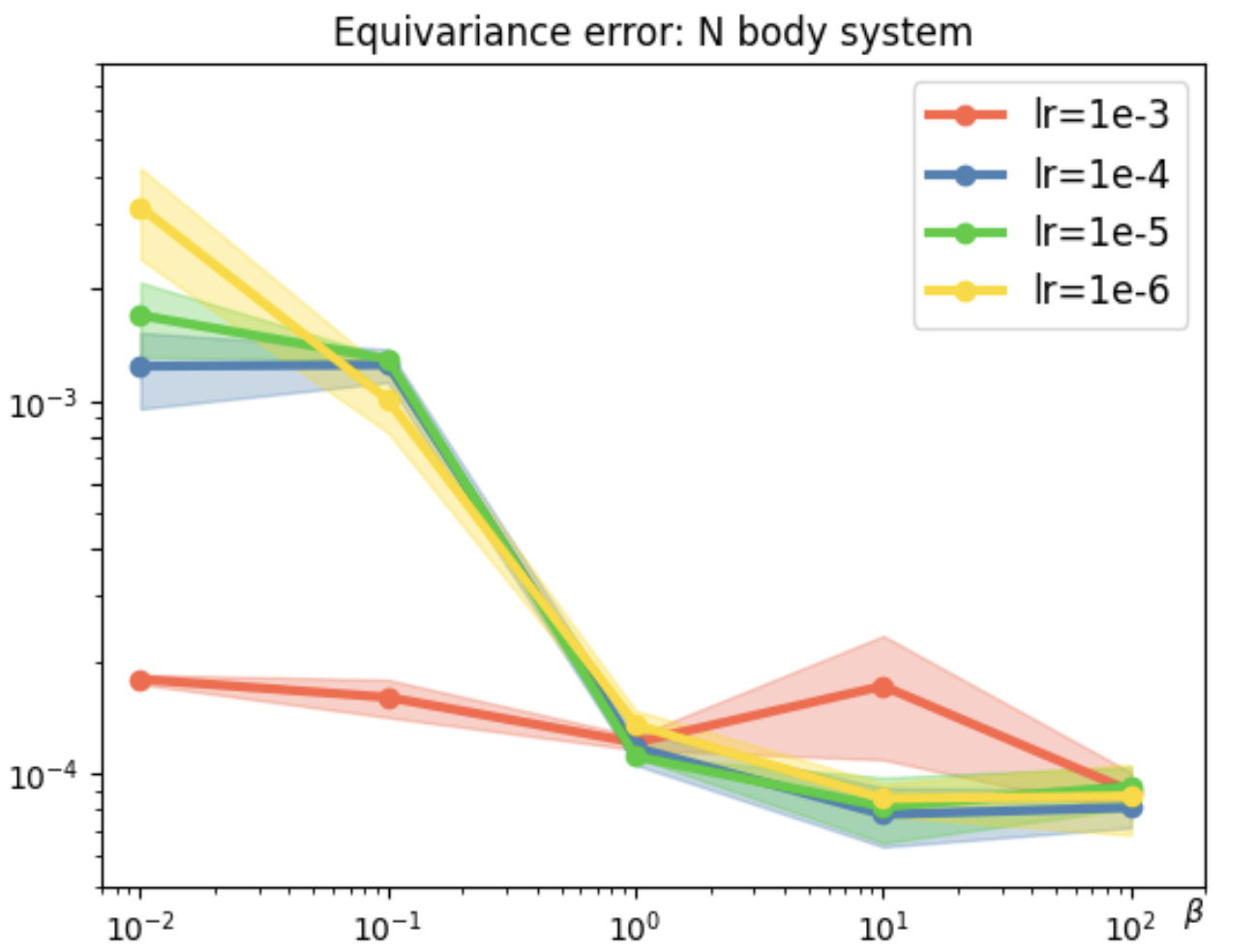
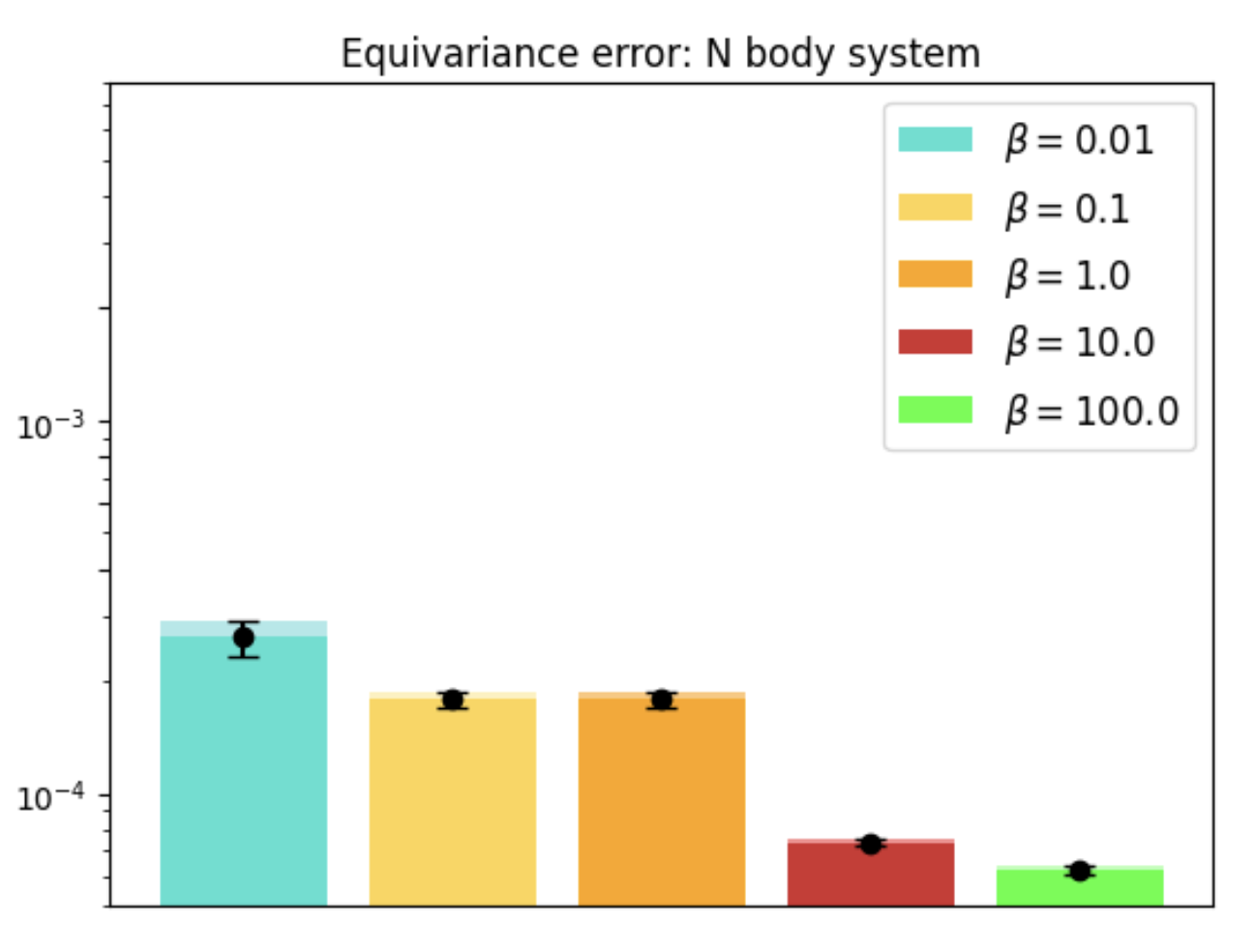
Figure 2: Evaluation on N-body dynamical system across scenarios and architectures.

Motion Capture

With real-world datasets like Motion Capture, REMUL-trained Transformers outperform equivariant models, showcasing remarkable flexibility in tasks without inherent symmetries. Optimal performance is achieved at intermediate levels of equivariance, emphasizing tailored symmetry considerations.

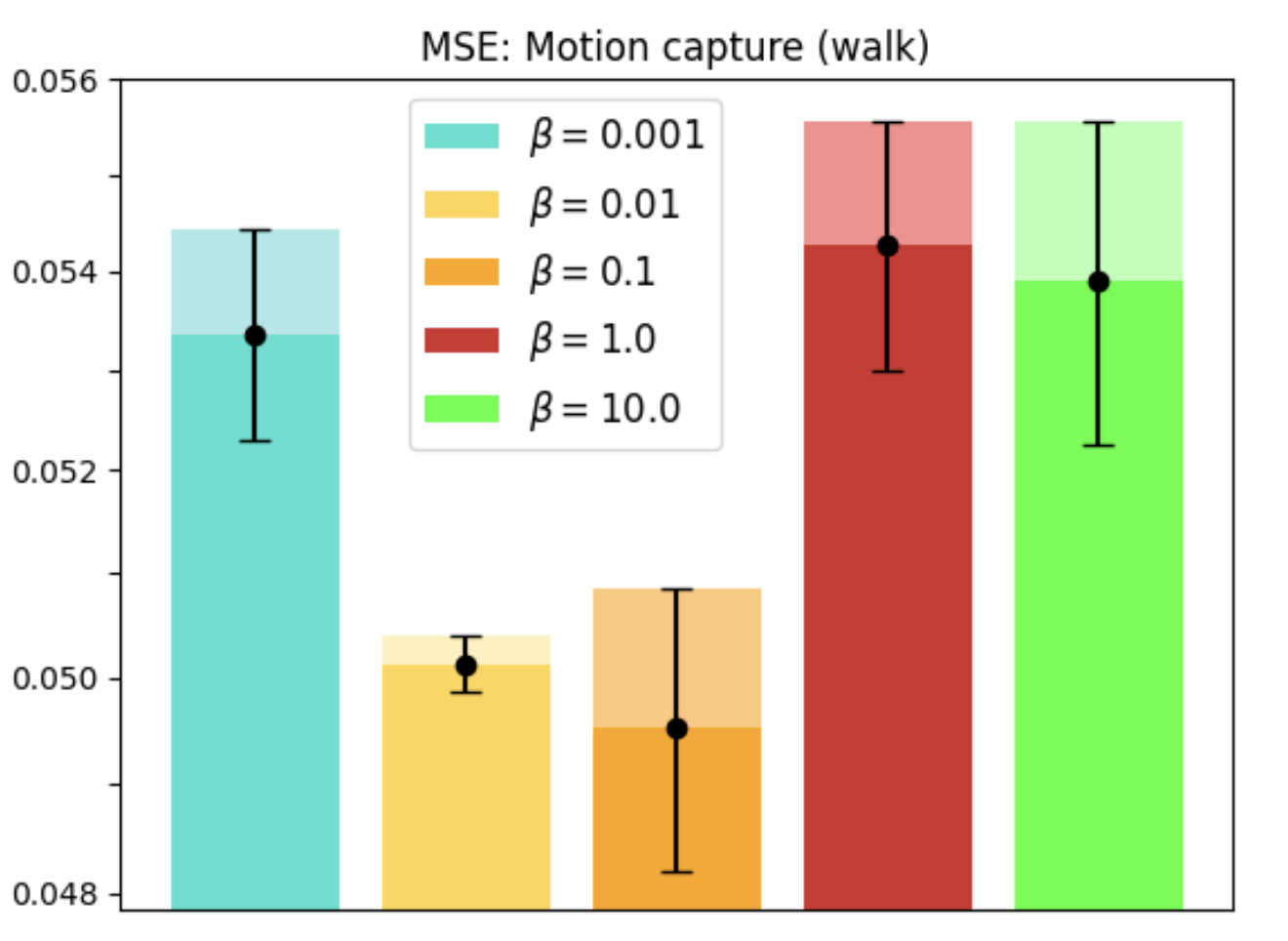
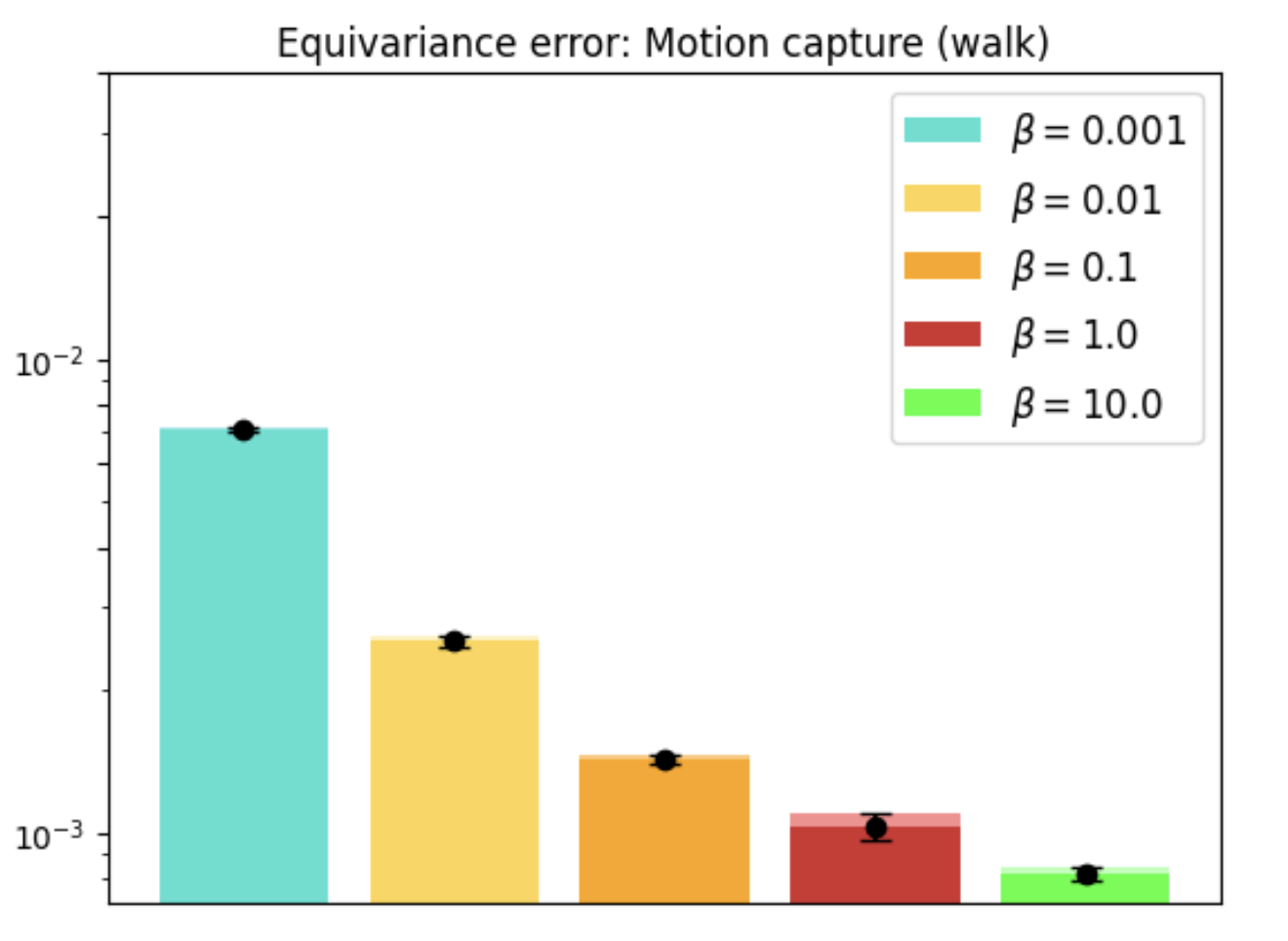
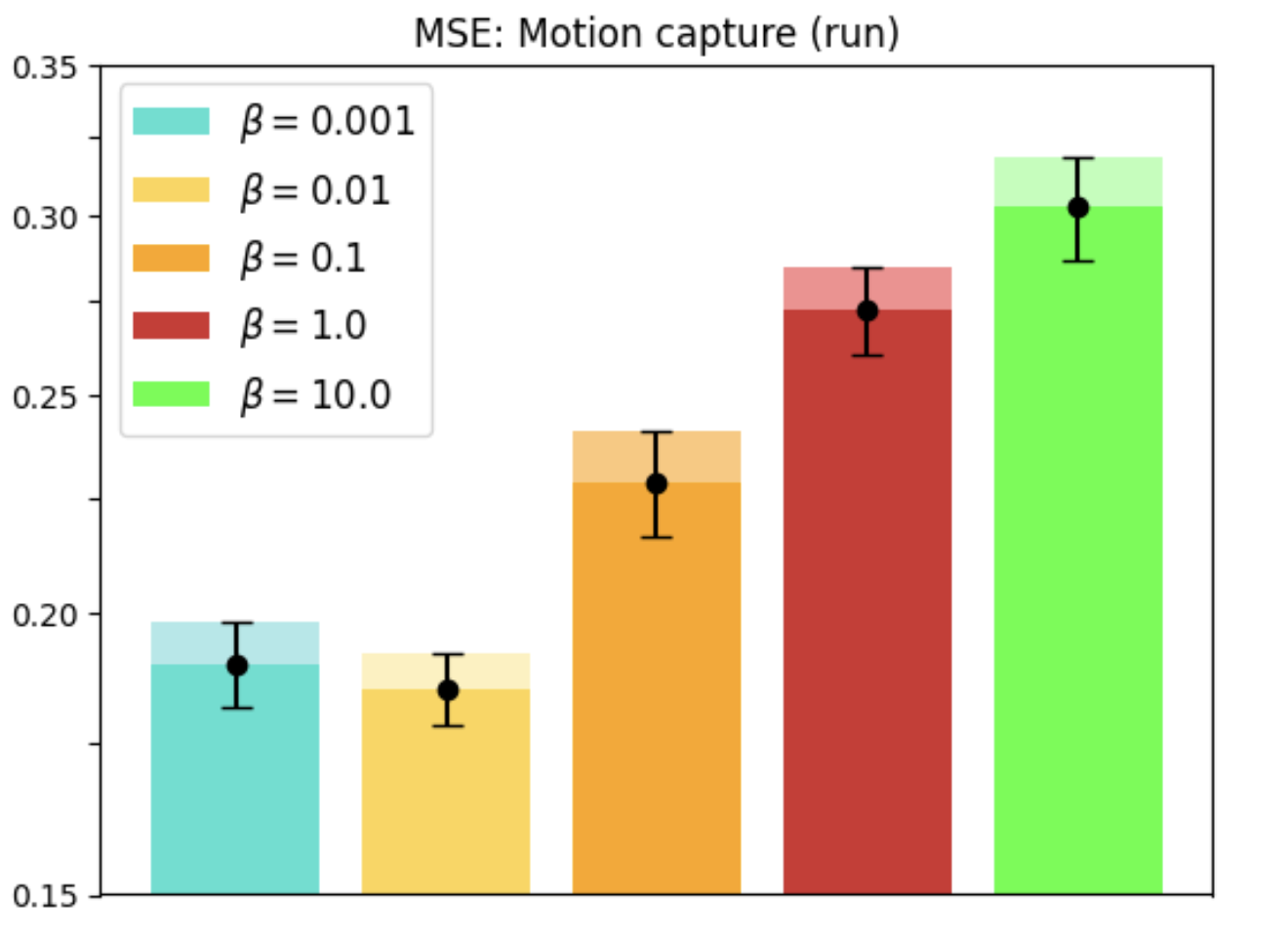
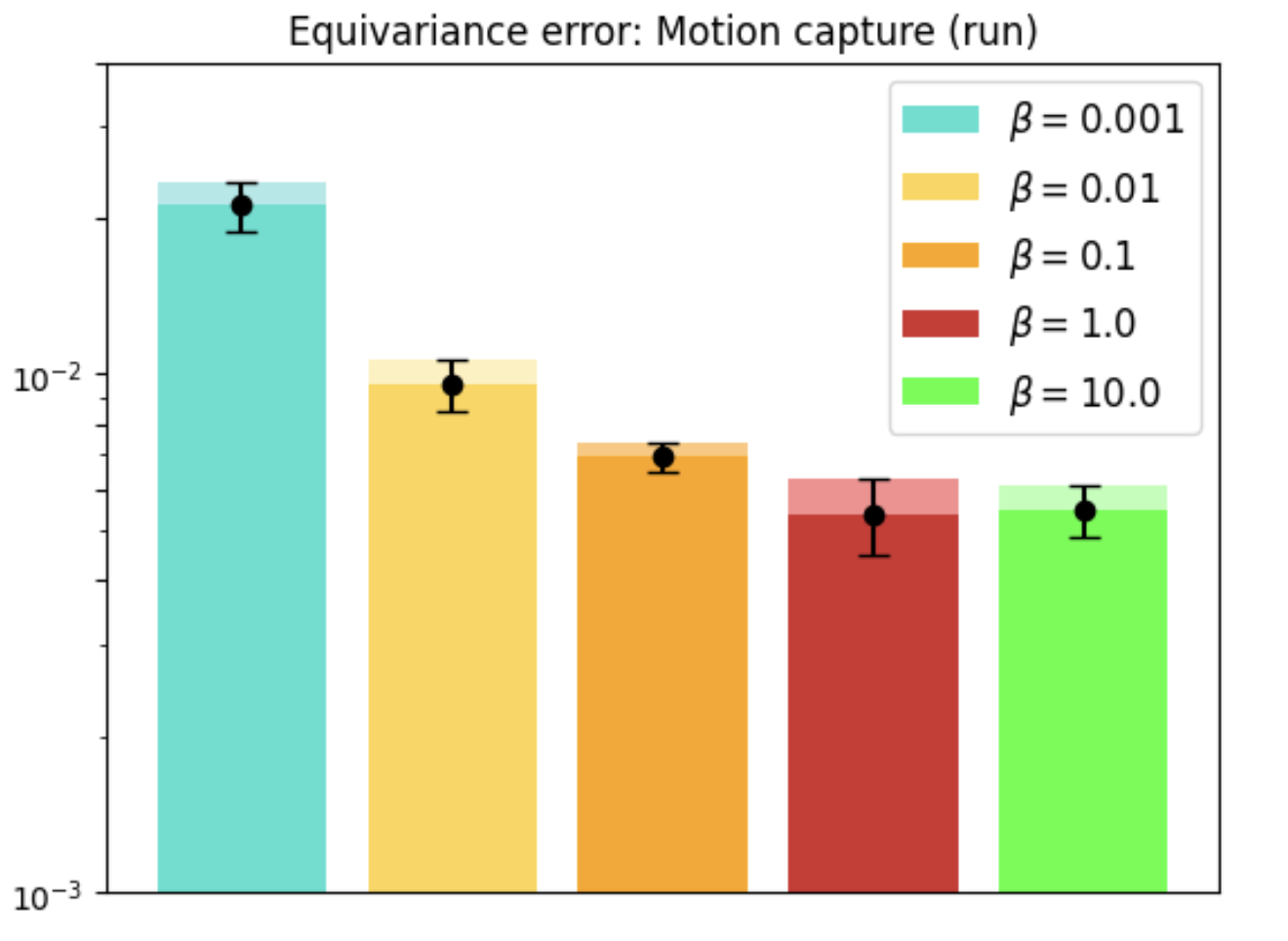
Figure 3: Motion Capture dataset evaluation showing the performance and equivariance error over walking and running tasks.

Molecular Dynamics

REMUL is also tested on molecular dynamics datasets, where GNNs trained with REMUL often surpass EGNNs in predicting complex molecular structures. The research indicates varying required levels of equivariance for optimal molecular predictions, reinforcing the importance of adaptive frameworks.

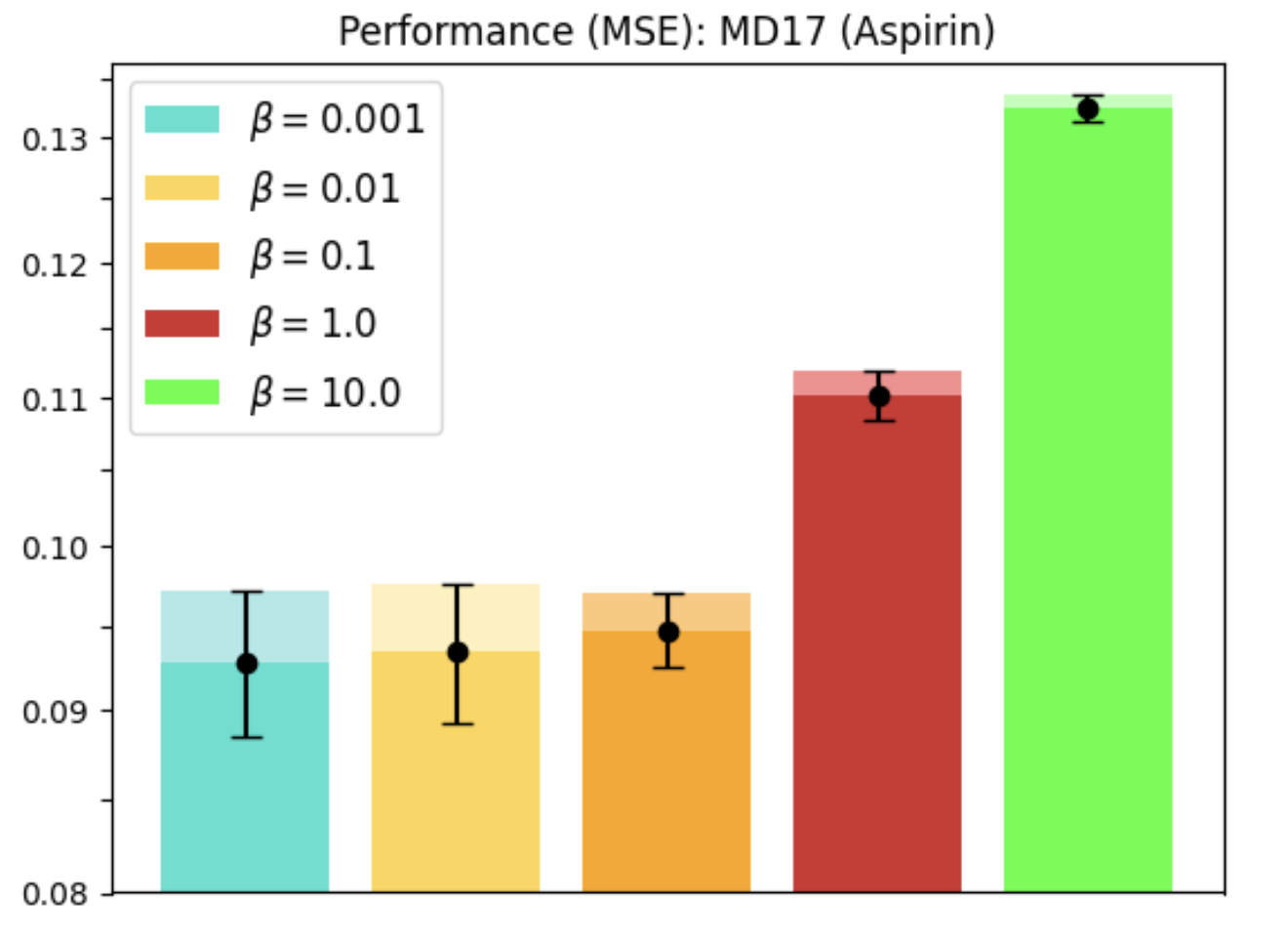
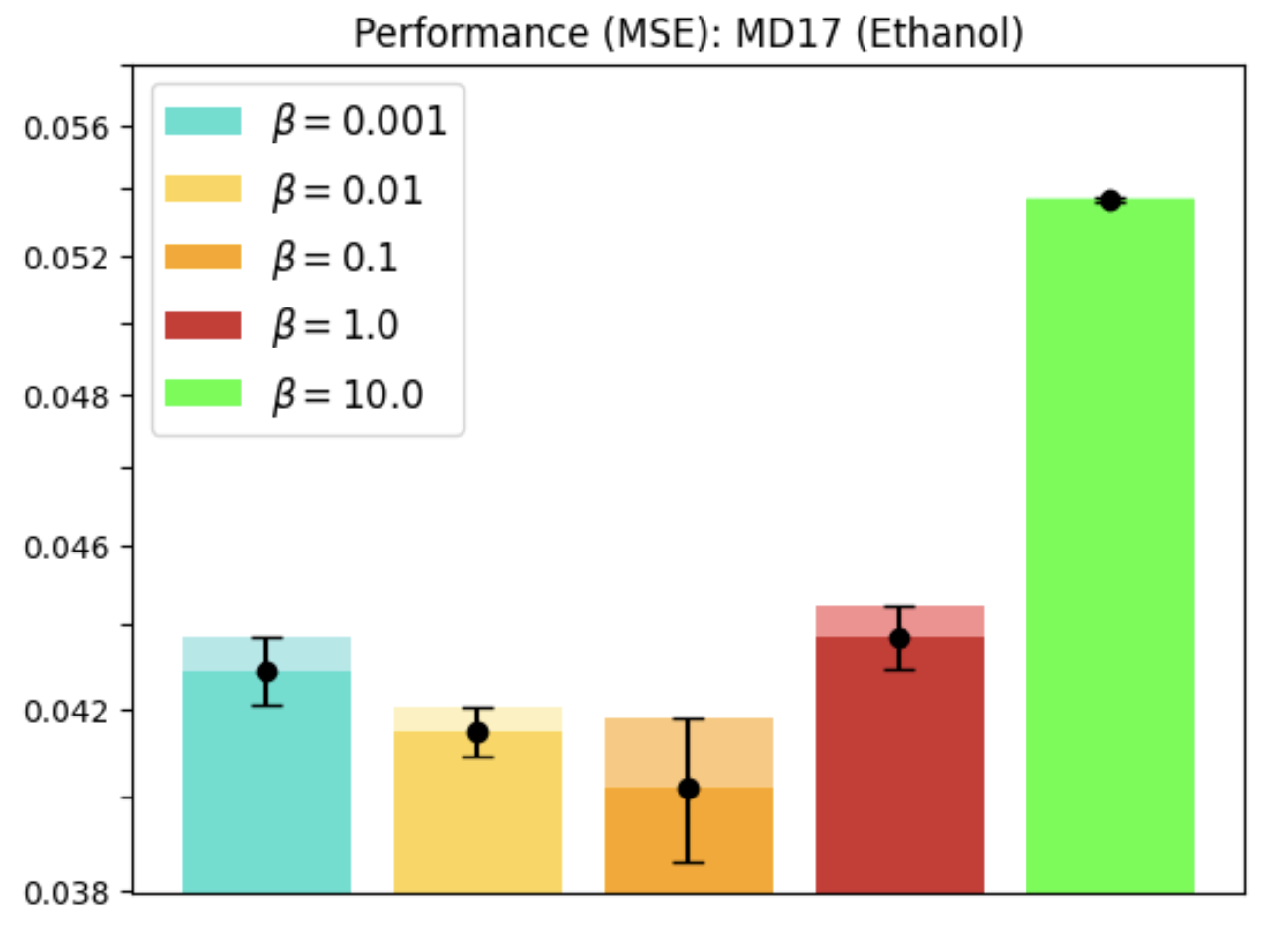
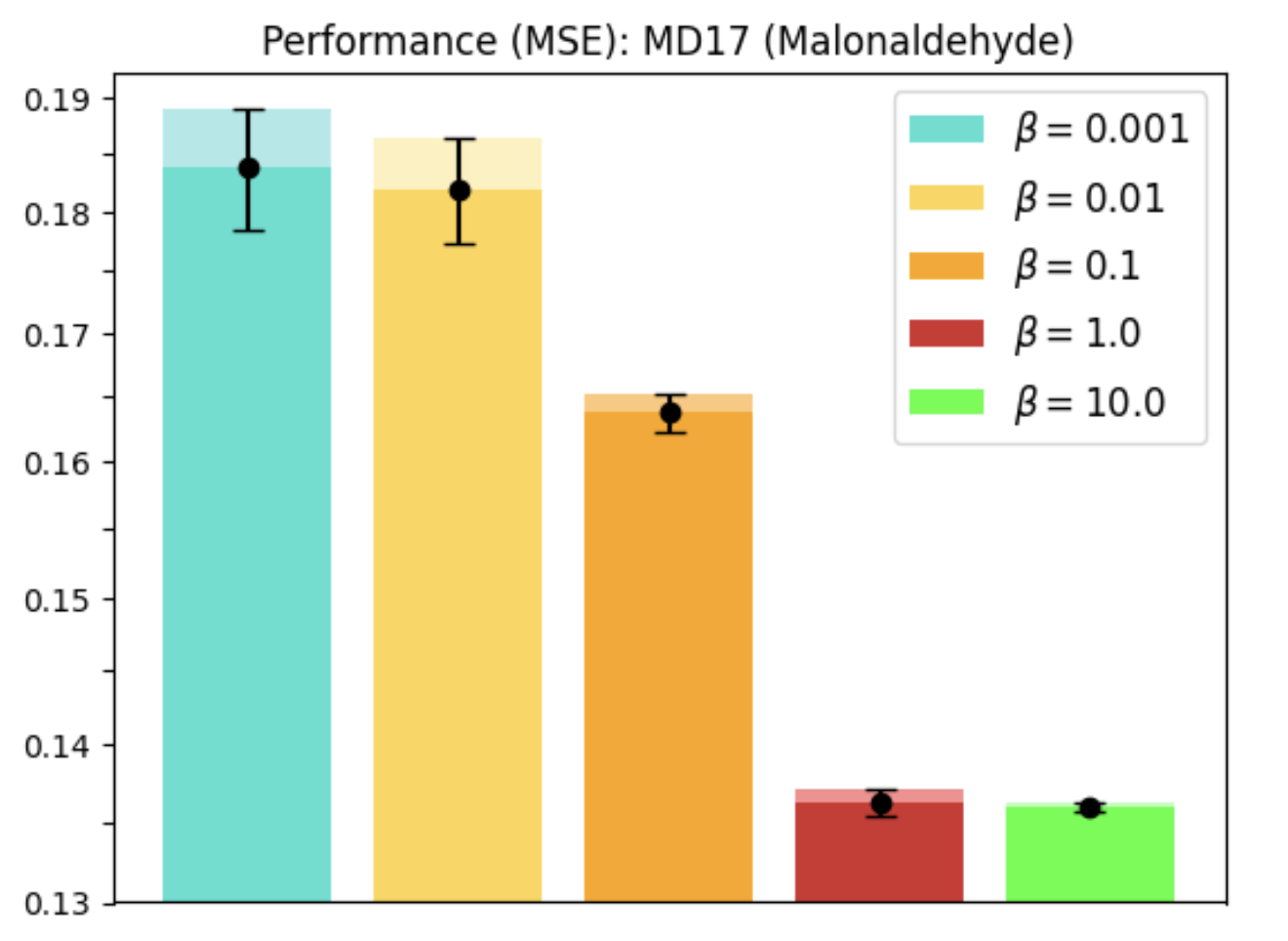
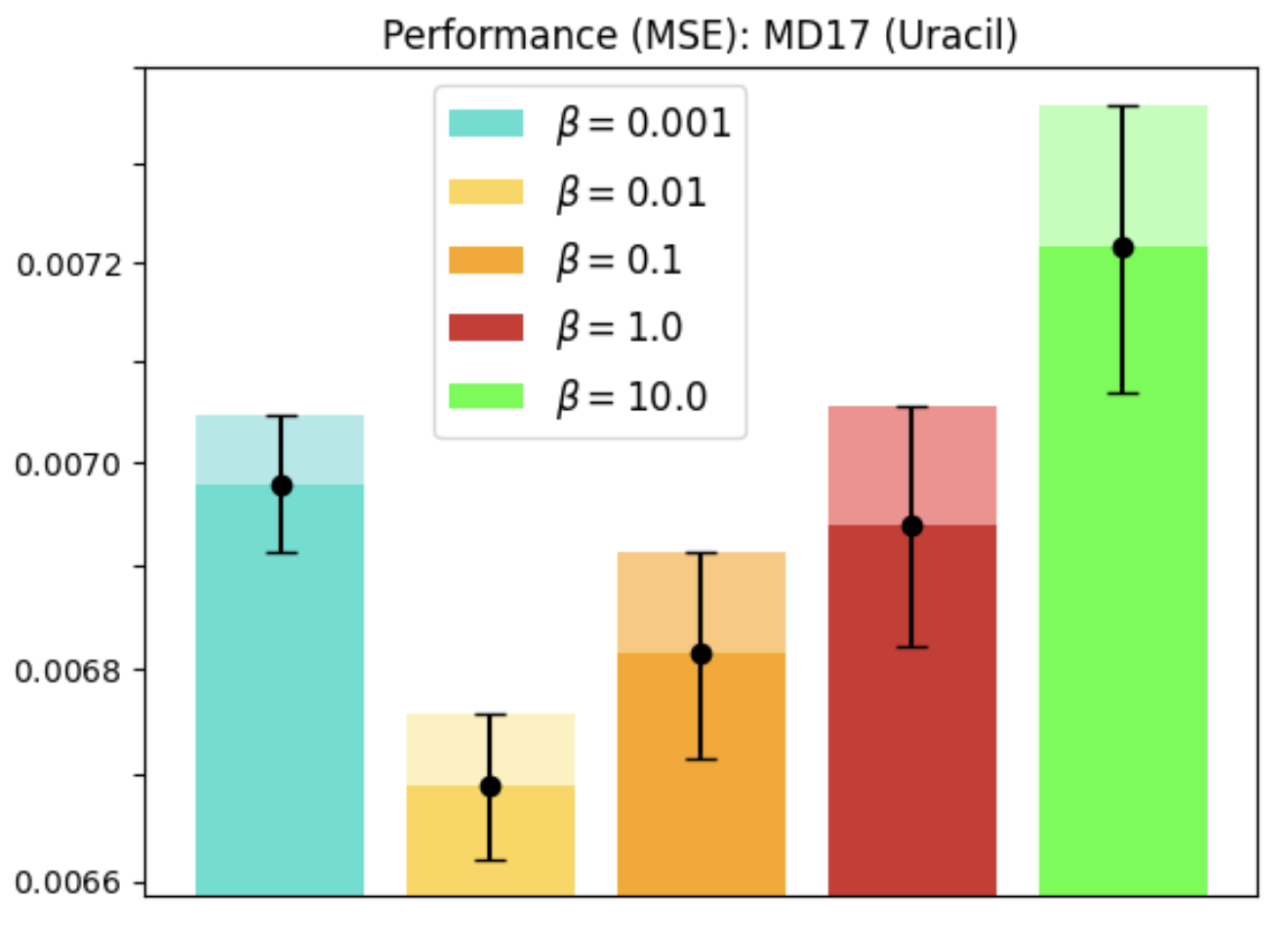
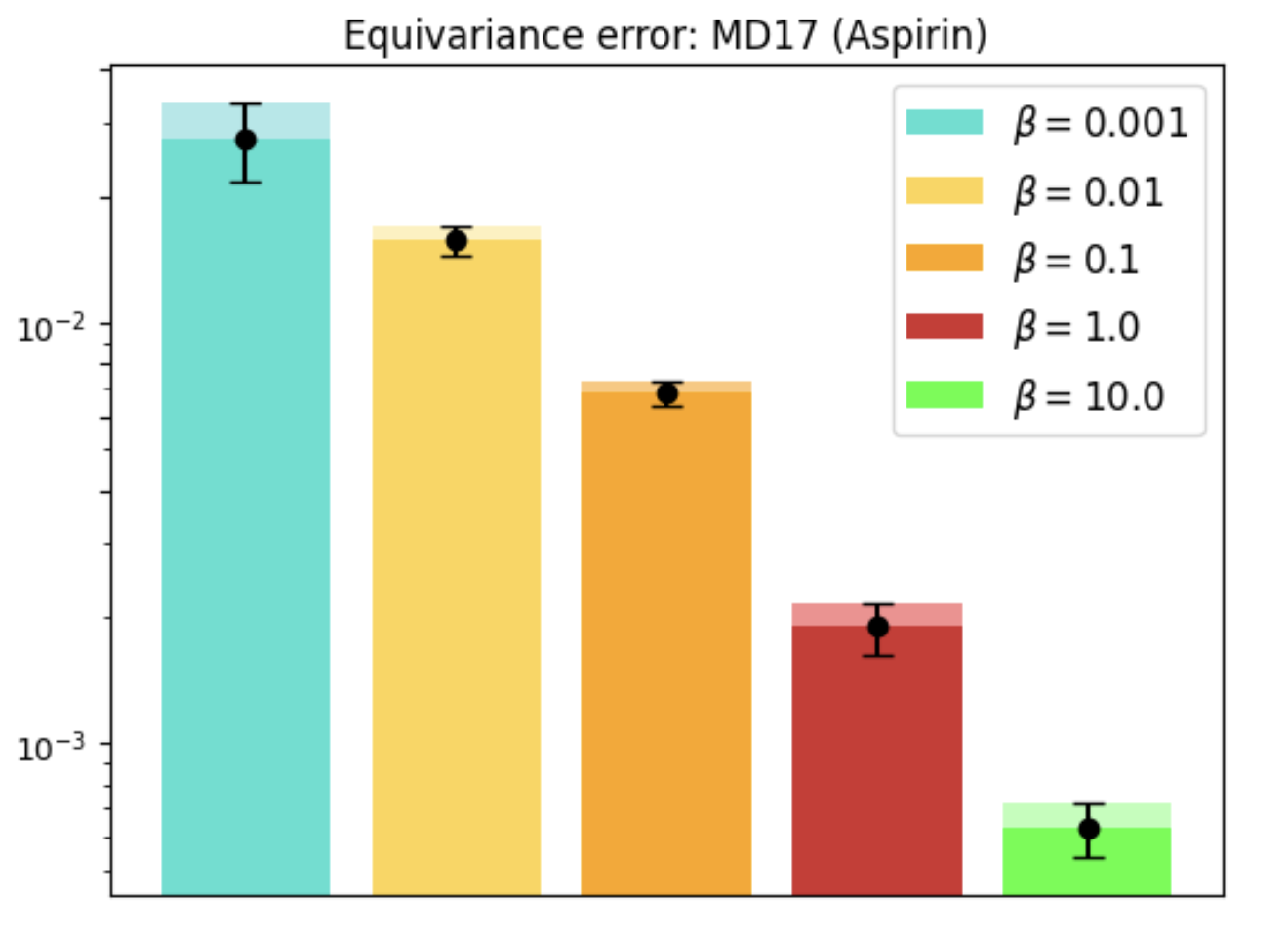
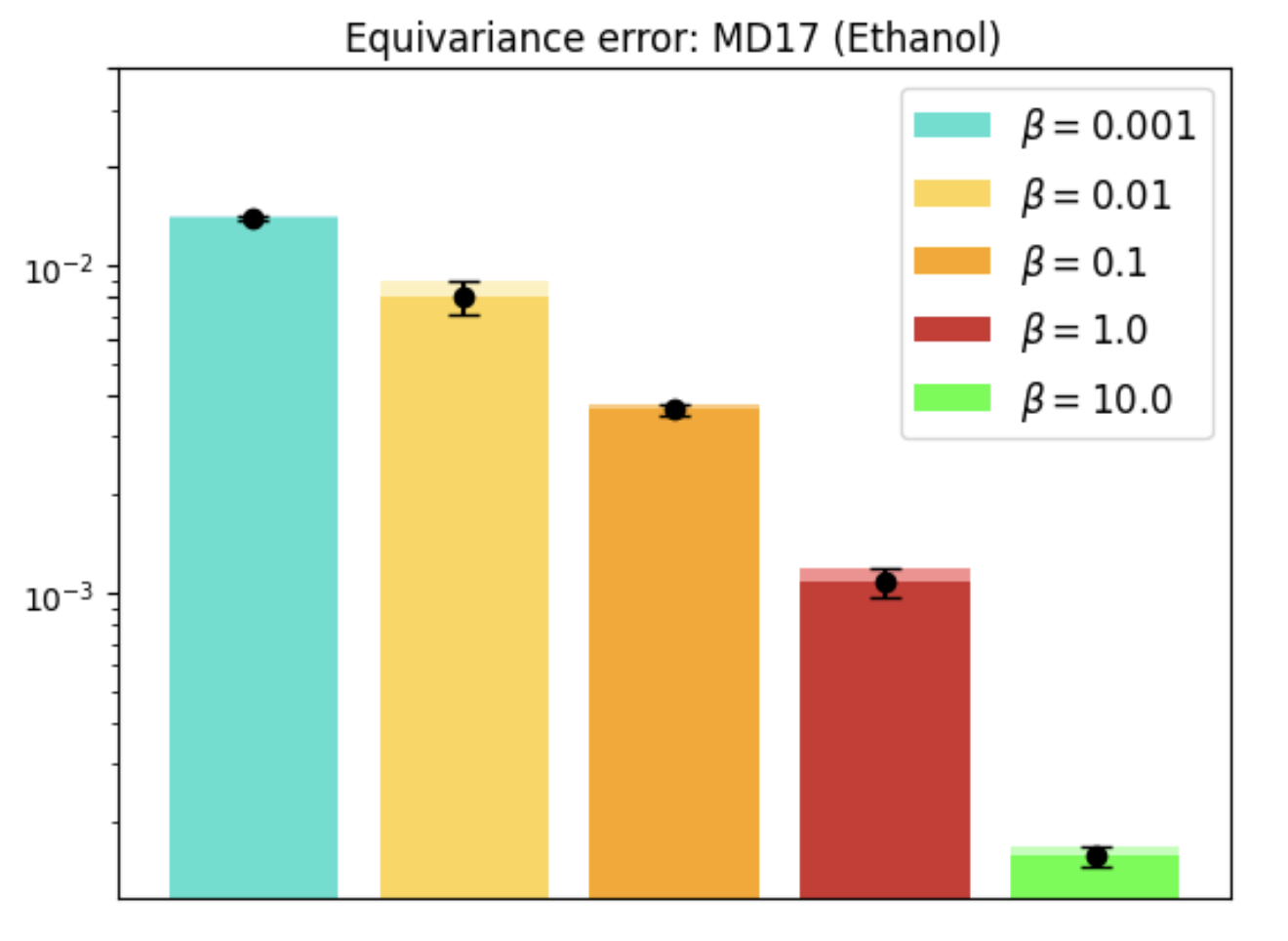
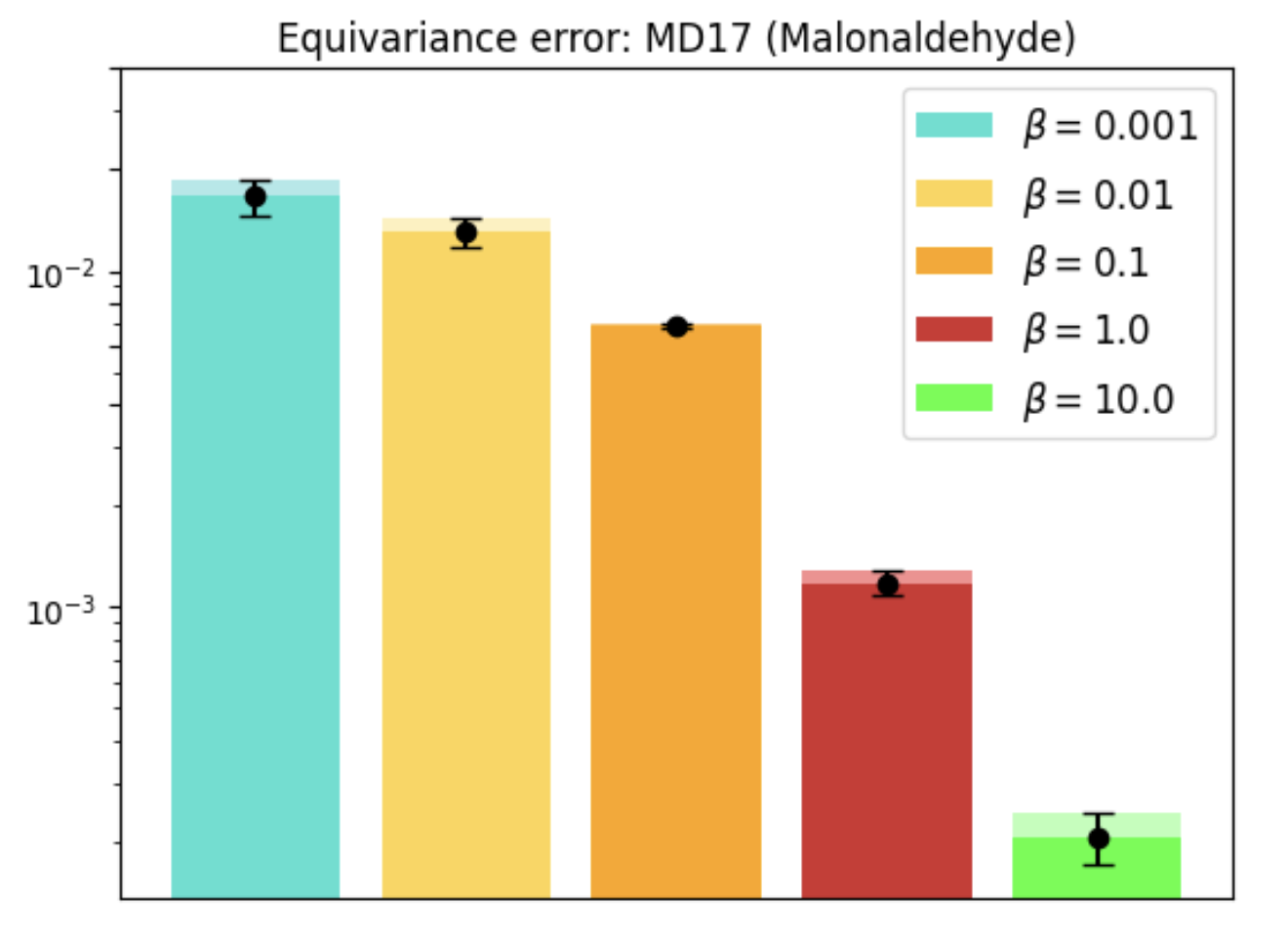
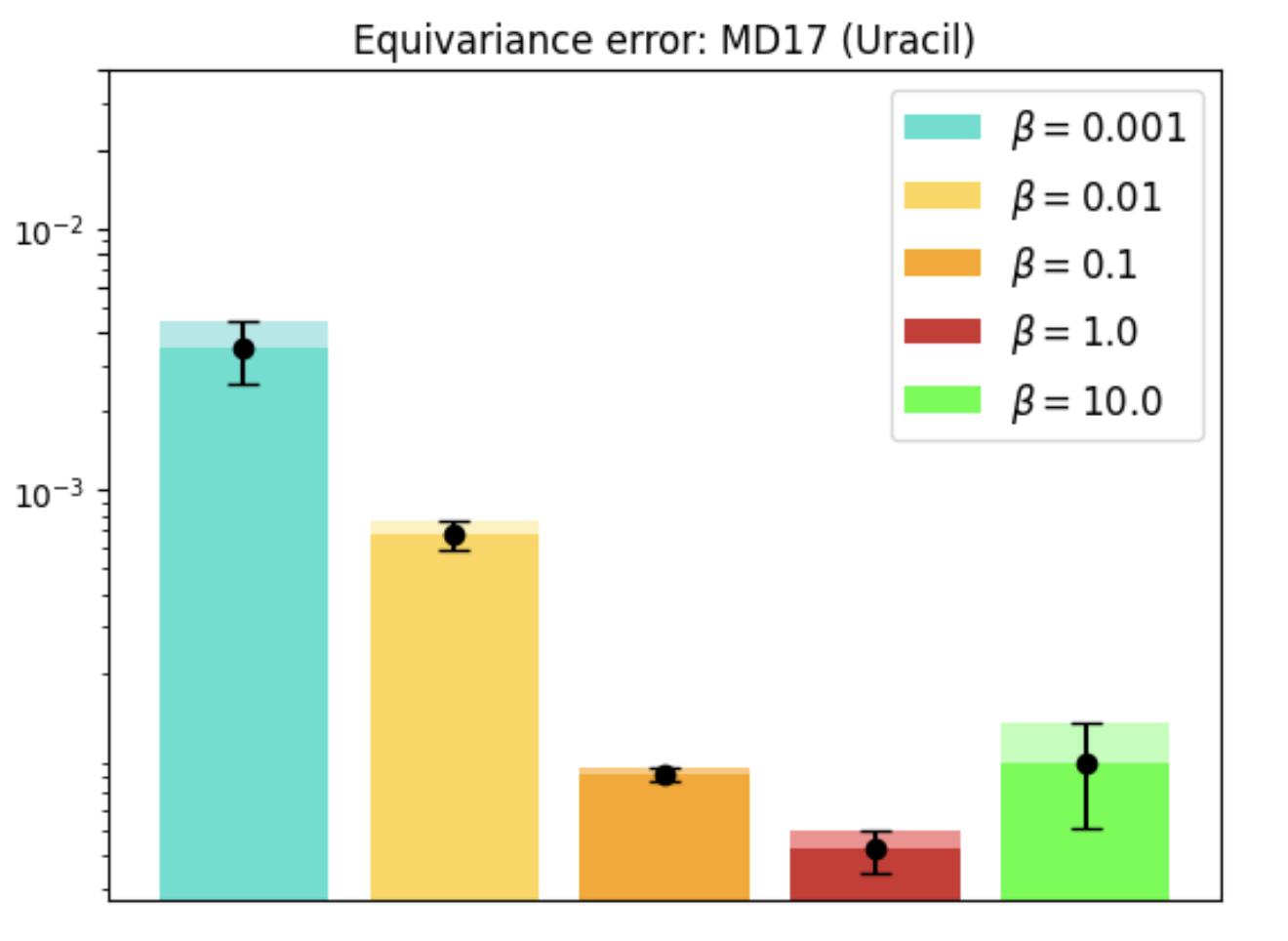
Figure 4: MD17 dataset performance and equivariance across molecules using REMUL-trained GNNs.

Computational Complexity and Loss Landscape

Empirical analysis of computational efficiency shows REMUL's significant speed advantages over Geometric Algebra Transformers, especially in training scenarios. Additionally, visualization of loss surfaces reveals more favorable optimization landscapes for REMUL-enhanced models compared to tightly constrained equivariant architectures.

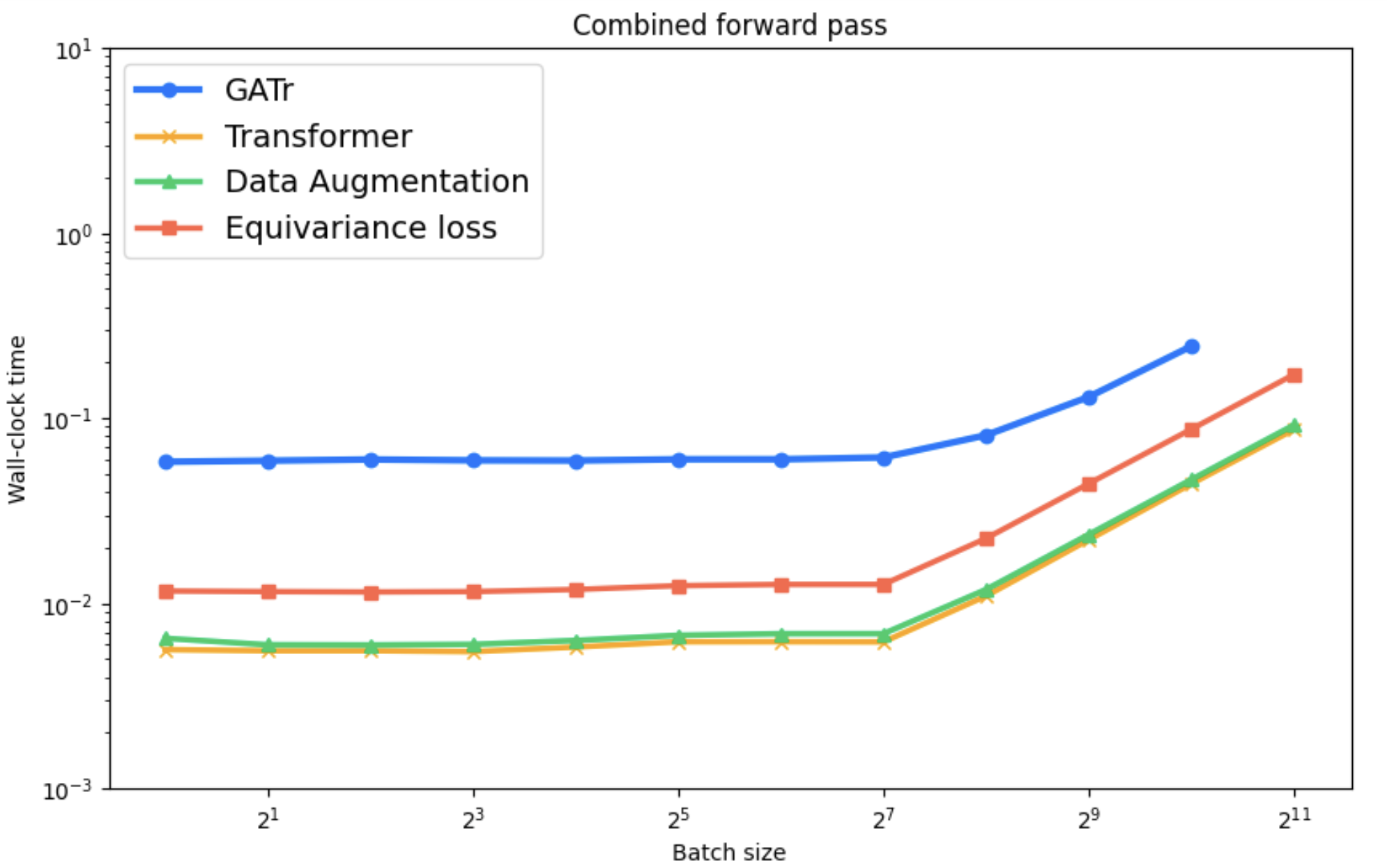
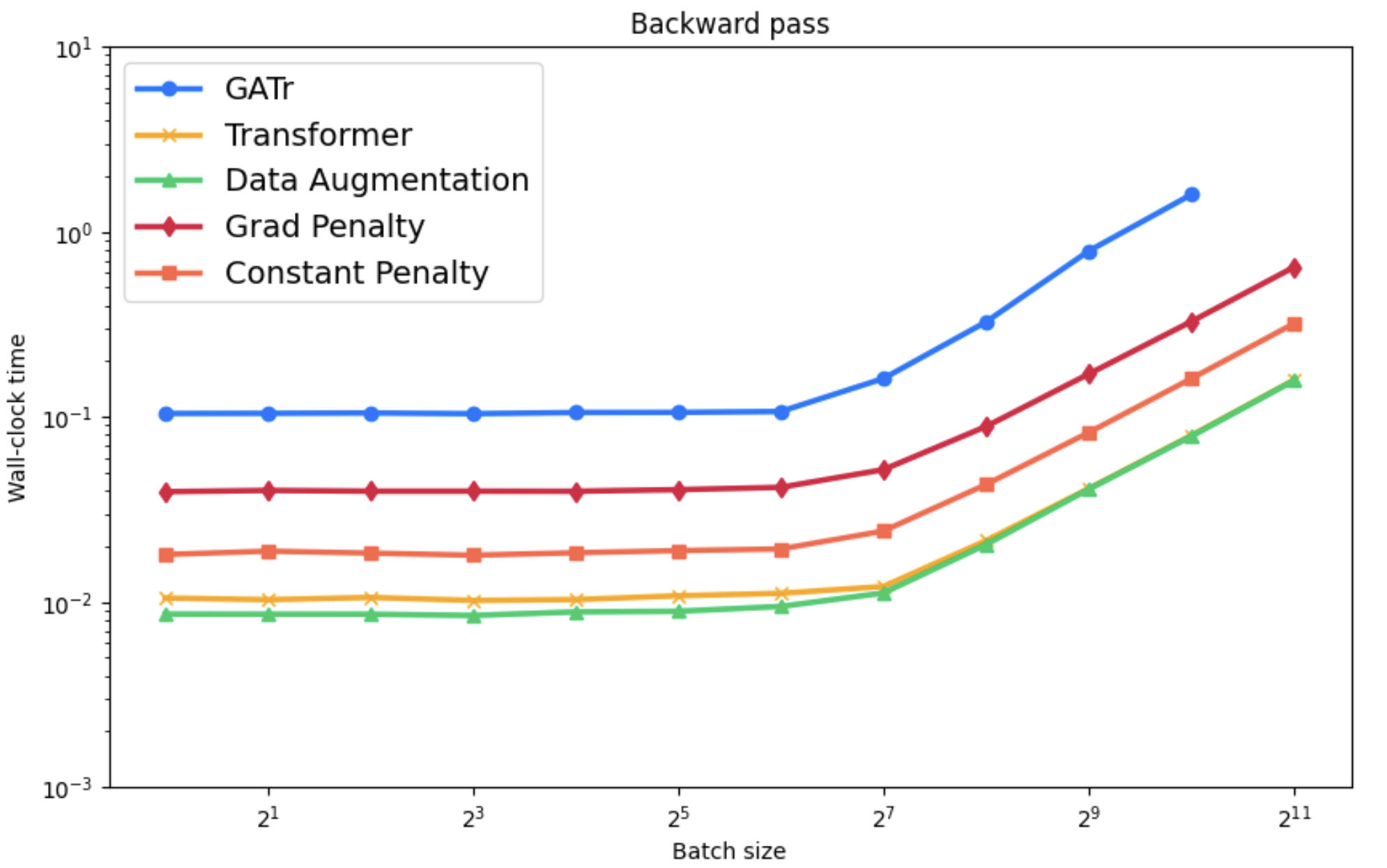
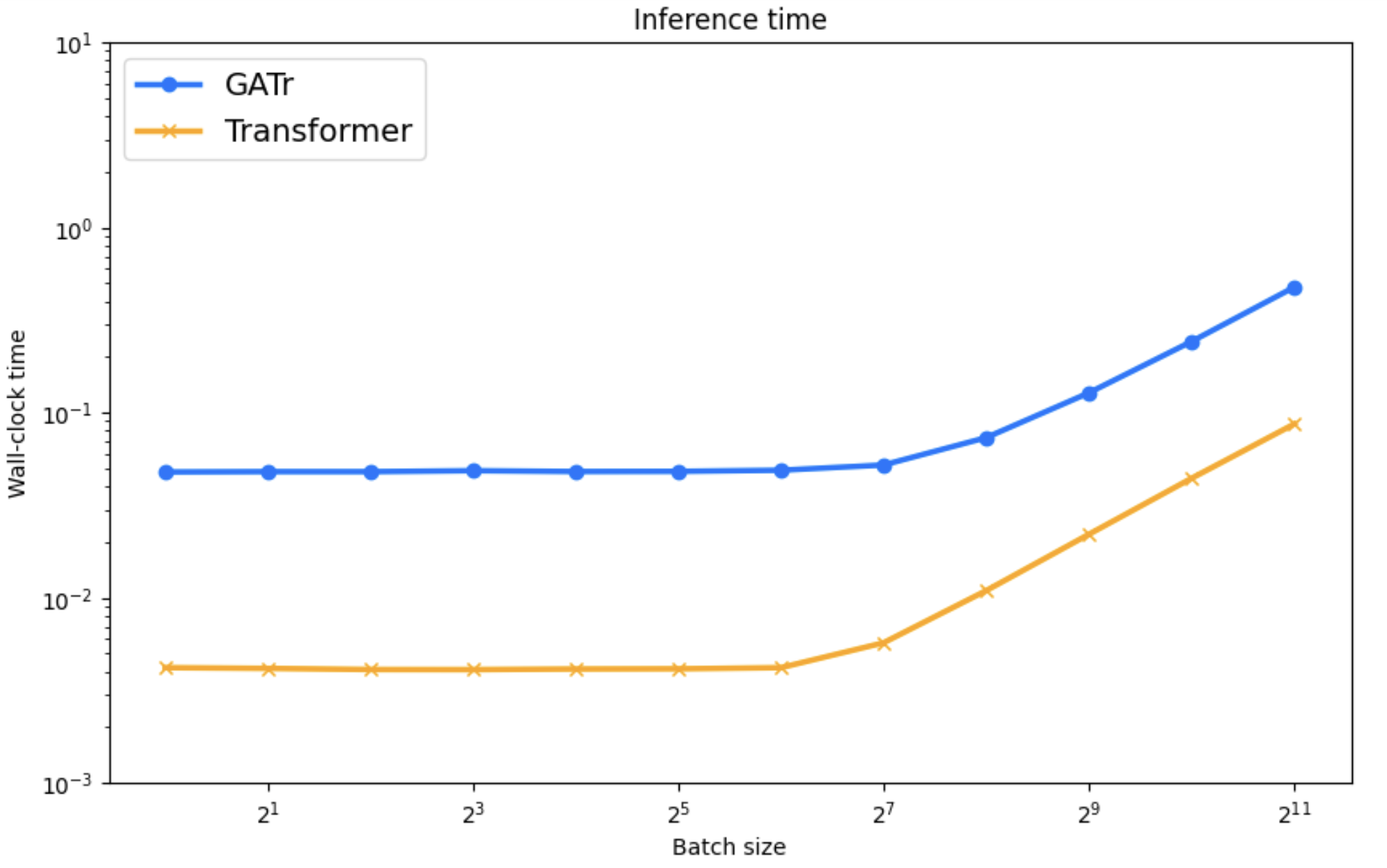
Figure 5: Computational time comparison displaying significant improvements with REMUL-trained models over GATr.

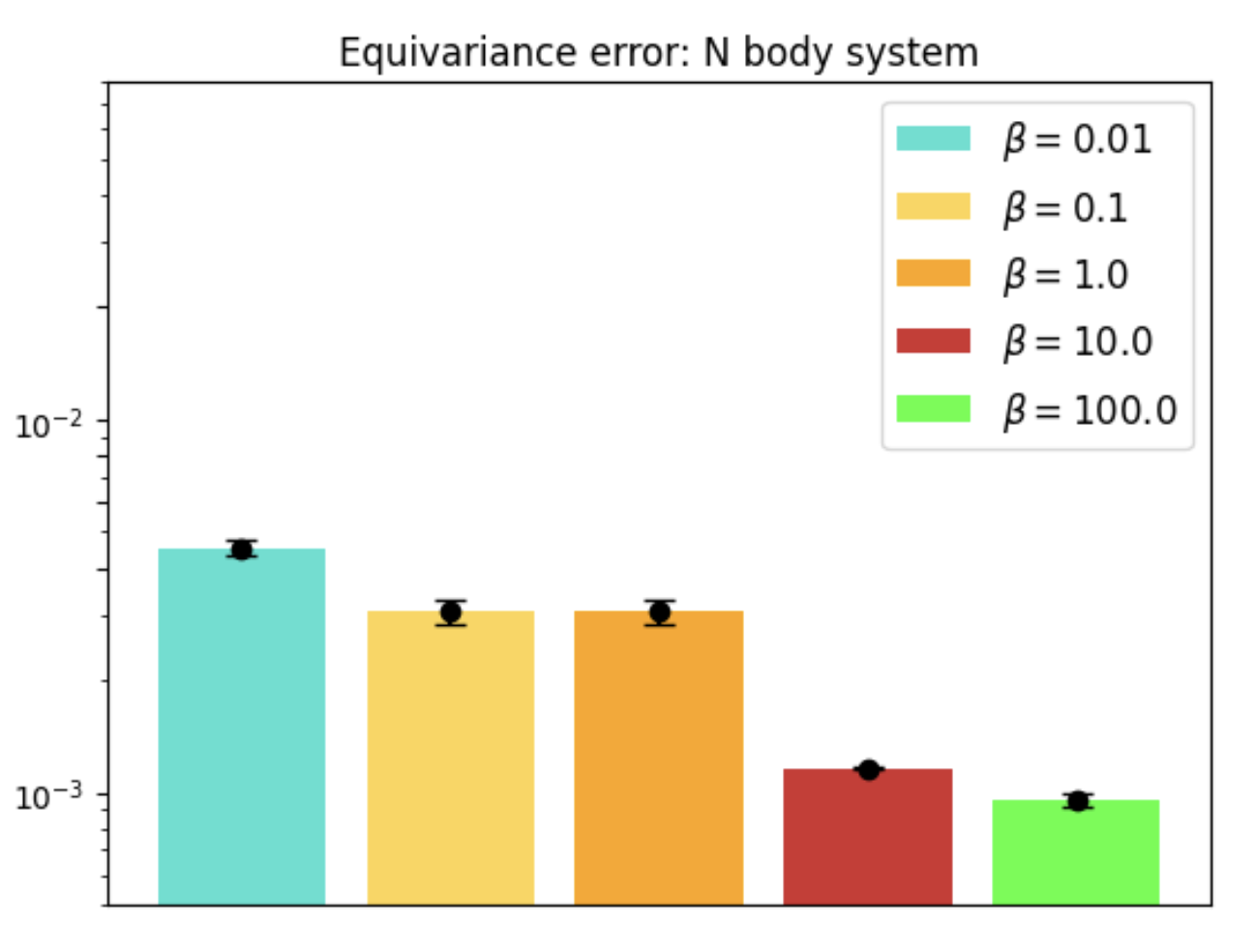
Figure 6: Loss surface visualization for Geometric Algebra Transformer and Transformer models.

Conclusion

REMUL provides a robust method for acquiring approximate equivariance in deep learning models, offering speed and flexibility over conventional approaches. This innovation facilitates real-world application scalability without sacrificing performance or adaptability. Future research may explore optimization pathways and initialization impacts on achieving model equivariance.

This research supports the advancement of unconstrained models in symmetrically complex domains, paving the way for more efficient and generalized AI systems.